An instant lottery ticket costs $2. Out of a total of 10,000 tickets printed for this lottery, 1000 tickets contain a prize of $5 each, 50 tickets have a prize of $10 each, 6 tickets have a prize of $1,000 each, and 1 ticket has a prize of $5,000. Let X be the random variable that denotes the net amount a player wins by playing this lottery.
Write the probability distribution of x. Enter the exact answers, Enter your answers for X in increasing order.
x P(x)
Determine the mean and standard deviation of x. Round your answers to two decimal places.
On average, the players who play this game expected to (lose/win) $_____ per ticket with a standard deviation of _____.
Answers
The players who play this game expected to lose $0.98 per ticket with a standard deviation of $145.87.
The probability distribution of X is given as follows:
X P(x)
-2 0.998
-1 0.002
5 0.1
10 0.005
1000 0.0006
5000 0.0001
To calculate the expected value of X, we can use the formula:
Expected value of X = ΣxP(x)
Therefore, the expected value is:
Expected Value of X = (-2) (0.998) + (-1) (0.002) + (5) (0.1) + (10) (0.005) + (1000) (0.0006) + (5000) (0.0001) = -0.98
The standard deviation of X is given by the expression:
Standard deviation of X = √(Σ(x-μ)²P(x))
Where μ is the expected value of X.
In this case, μ = -0.98
Therefore, the standard deviation of X is:
Standard deviation of X = √(((-2 - (-0.98))²) (0.998) + ((-1 - (-0.98))²) (0.002) + ((5 - (-0.98))²) (0.1) + ((10 - (-0.98))²) (0.005) + ((1000 - (-0.98))²) (0.0006) + ((5000 - (-0.98))²) (0.0001))
= √(145.87)
= 12.07
Therefore, the players who play this game expected to lose $0.98 per ticket with a standard deviation of $145.87.
Learn more about the standard deviation visit:
brainly.com/question/13905583.
#SPJ4
Related Questions
Question: Replace the question mark in the above problem with the appropriate number.

Answers
Answer:
Step-by-step explanation:
6
Answer: 6 lol wowwwwwwwwwwwwwwwwwwwww
PLS HELP FAST WILL GIVE BRAINLIEST
The trees on two different plots of land are tested for disease. The results are shown in this table.
Enter numbers in the boxes so that the two-way table represents these results.
Plot A Plot B
Disease present
Disease not present
Tree Plot Disease present?
1 A Y
2 A N
3 B Y
4 B Y
5 B Y
6 A N
7 B N
Answers
Answer:
The values are calculated with the help of table.
Step-by-step explanation:
We are given the following information in the question:
A table is shown showing trees on two different plots of land which are tested for disease.
Tree: 1 2 3 4 5 6 7
Plot: A A B B B A B
Disease: Y N Y Y Y N N
We have to find:
Calculating from the table, we can fill the values as:
Plot A Plot B
Disease Present 1 3
Disease not Present 2 1
Answer:
Disease Present
Plot A: 1
Plot B: 3
Disease Not Present
Plot A: 2
Plot B: 1
The ordered pairs (0, 2) and (1,6)
are solutions to an exponential
equation. Find a and b. Write the
equation.
Answers
Answer:
y=4x+6
Step-by-step explanation:
Determine algebraically the number of cats and the number of dogs Bea initially had in her pet shop.
Answers
The equation or system of equations that can be used to determine the number of cats and dogs Bea has in her pet shop is d = 2c - 5 d + 3 = c + 3. We can solve the system of equations using substitution and plug it back into either equation to find the value of d, which is 8 cats and 10 dogs.
How will we determine the number of cats and doge Beas initially had in her pet shop?The equation or system of equations that can be used to find the number of cats and dogs Bea has in her pet shop is:
d = 2c - 5
d + 3 = c + 3
No, Bea's Pet Shop could not initially have 15 cats and 20 dogs. This is because the equation or system of equations states that the number of dogs is five less than twice the number of cats, which would mean that 15 cats would result in 25 dogs, which is not equal to 20.
To determine algebraically the number of cats and the number of dogs Bea initially had in her pet shop, we can use the equation or system of equations that we previously created.
d = 2c - 5
d + 3 = c + 3
We can solve the system of equations using substitution:
d = 2c - 5
d + 3 = c + 3
d + 3 = c + 3
d = c + 3
2c - 5 = c + 3
2c = c + 8
c = 8
Once we determine the value of c, we can plug it back into either equation to find the value of d:
d = 2(8) - 5
d = 15 - 5
d = 10
Therefore, Bea initially had 8 cats and 10 dogs in her pet shop.
To know more about algebra, visit
brainly.com/question/24875240
#SPJ1
The complete question is: At Bea's Pet Shop, the number of dogs, d, is initially five less than twice the number of cats, c. If she decides to add three more of each, the ratio of cats to dogs will be – Write an equation or system of equations that can be used to find the number of cats and dogs Bea has in her pet shop. Could Bea's Pet Shop initially have 15 cats and 20 dogs? Explain your reasoning. Determine algebraically the number of cats and the number of dogs Bea initially had in her pet shop.
how many ways are there for her to plan her schedule of menus for the 20 school days if there are no restrictions on the number of times she cooks a particular type of meal?
Answers
The number of ways to plan her schedule of menus for the 20 school days is 10^20.
How to many number of ways to plan her schedule?To calculate combinations, we will use the formula nCr = n! / r! * (n - r)!, where n represents the total number of items, and r represents the number of items being chosen at a time. To calculate a combination, you will need to calculate a factorial.
For each day, there are ten different choices for what she will cook that day. 20 decisions are made, one for each day with ten different possibilities for each choice.
The complete question is: A school cook plans her calendar for the month of February in which there are 20 school days. She plans exactly one meal per school day. Unfortunately, she only knows how to cook ten different meals.
How many ways are there for her to plan her schedule of menus for the 20 school days if there are no restrictions on the number of times she cooks a particular type of meal?
To learn more about number of ways refer to:
https://brainly.com/question/25966410
#SPJ1
A grapefruit is launched up into the air with a modified catapult In give by h (t)=15+60-1642 models the grapefruit's hei Select all the true statements about the situation. The grapefruit will hit the ground at 3 seconds. The valt 10 does not belong to the domain of h. The grapefruit is 15 feet above the ground when it is launched. The domain of function if only contains values greater than or equal to 0. 016-gravity will have on the grapefruit. OTH ame height 1 second after launch and 2 seconds after launch
Answers
The true statements are The grapefruit is 15 feet above the ground when it is launched. The domain of the function h only contains values greater than or equal to 0.
The grapefruit will hit the ground at 3 seconds.
This statement cannot be determined solely based on the given information. The equation provided, h(t) = 15 + 60t - 16t^2, represents the height of the grapefruit as a function of time. To determine when the grapefruit hits the ground, we need to find the value of t for which
h(t) = 0.
The value 10 does not belong to the domain of h.
The domain of the function h(t) is determined by the restrictions on the variable t. In this case, since h(t) represents the height of the grapefruit, it should be defined for all values of t that are relevant to the situation. From the given information, it is not clear whether the domain includes or excludes the value 10. Therefore, we cannot determine the validity of this statement.
The grapefruit is 15 feet above the ground when it is launched.
According to the equation h(t) = 15 + 60t - 16t^2, the initial height when t = 0 is 15 feet. Therefore, this statement is true.
The domain of the function h only contains values greater than or equal to 0.
The domain of a function represents the set of all valid inputs for the function. In this case, since t represents time, it cannot be negative. Therefore, the domain of h is indeed values greater than or equal to 0. This statement is true.
The same height 1 second after launch and 2 seconds after launch.
To determine if the grapefruit reaches the same height 1 second after launch and 2 seconds after launch, we need to evaluate the function h(t) at those time points.
At t = 1 second, h(1) = 15 + 60(1) - 16(1)^2 = 15 + 60 - 16 = 59 feet.
At t = 2 seconds, h(2) = 15 + 60(2) - 16(2)^2 = 15 + 120 - 64 = 71 feet.
Therefore, the grapefruit does not reach the same height 1 second after launch and 2 seconds after launch. This statement is false.
In summary, the true statements are The grapefruit is 15 feet above the ground when it is launched. The domain of the function h only contains values greater than or equal to 0.
For more such questions on feet , Visit:
https://brainly.com/question/24657062
#SPJ11
how can you compare proportional relationships represented in different ways?
Answers
Answer:
Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways. For example, compare a distance-time graph to a distance-time equation to determine which of two moving objects has greater speed.
Step-by-step explanation:
Solve each equation. Check your answers.
2 log₃ x - log₃ 4=2
Answers
The solution to the given equation is x = 6.
The given equation is 2log₃x − log₃4 = 2.
To solve this equation, we use the following properties of logarithms:
Product property: log a + log b = log ab. Quotient property:
log a − log b = log (a/b). Power property: log aⁿ = n log a.
Here, we will use the product and power properties of logarithms to simplify the given equation, and then solve for x:
2log₃x − log₃4 = 22log₃x = log₃(4 · 3²)
[using the product and power properties of logarithms]2log₃x = log₃36log₃x = log₃6²2log₃x = 2 log₃6
[using the power property of logarithms]
log₃x = log₃6x = 6
Thus, the solution to the given equation is x = 6.
Let's check our answer:
2log₃x − log₃4 = 2 ⇒ 2log₃6 − log₃4 = 2log₃36 − log₃4 = 2(log₃36/4) = 2log₃9 = 2(2) = 4 [using the quotient and power properties of logarithms]
Thus, the solution x = 6 is correct.
Learn more about logarithms from the given link
https://brainly.com/question/25710806
#SPJ11
What is the mode for this list of numbers? 5, 9, 12, 11, 12, 19, 18
Answers
The mode is one of the measures of central tendency in statistics. It represents the number that appears most frequently in a given list of numbers. In the example above, the mode for the list of numbers {5, 9, 12, 11, 12, 19, 18} is 12.
The mode is defined as the number that occurs most frequently in a list of numbers. In a set of numbers, there can be one mode, more than one mode, or no mode at all.
To find the mode for the list of numbers {5, 9, 12, 11, 12, 19, 18}, we need to identify the number that appears most frequently. Here, we can observe that 12 is the number that appears twice, while all the other numbers only appear once.
Therefore, the mode for this list of numbers is 12. It's important to note that if there are multiple numbers that appear with the same highest frequency, then all of them are considered as modes. For instance, if the list of numbers was {5, 9, 12, 11, 12, 19, 19, 18}, then both 12 and 19 would be modes since they each appear twice.
In conclusion, the mode is one of the measures of central tendency in statistics. It represents the number that appears most frequently in a given list of numbers. In the example above, the mode for the list of numbers {5, 9, 12, 11, 12, 19, 18} is 12.
For more such questions on frequently
https://brainly.com/question/29985480
#SPJ8
Law of cosines: a2=b2+c2-2bccos(A)
What is the measure of angle N to the nearest whole degree
Answers
The measure of the angle N will be 82.8 degrees.
What is the law of cosines?The square of the length of any one side of a triangle is equal, by the cosine rule, to the sum of the squares of the lengths of the other two sides, multiplied by the cosine of the angle they are a part of.
Given that the formula form cosine law is,
a²=b²+c²- 2.bc.cos(A)
Let us assume the values a = 6, b = 5, and c = 4. The angle N will be calculated as:-
a²=b²+c²- 2.bc.cos(A)
6² = 5² + 4² - 2 x 5 x 4 cos(A)
36 = 25 + 16 - 40cos(A)
-5 = - 40cosA
cosA = 1 / 8
A = cos⁻¹( 1 / 8 )
A = 82.81°
Therefore, the value of angle N is 82.81°
To know more about the law of cosines follow
https://brainly.com/question/4372174
#SPJ1
Consider a fractal line with fractal dimension D. The mean-square distance between monomers u and v along this line is ⟨(R(u)−R(v))2⟩=b2(v−u)2/D. Calculate the mean-square end-to-end distance R2 and radius of gyration Rg2 for this fractal line. Determine the ratio R2/Rg2 symbolically and then calculate this ratio for fractal dimensions D=1,1.7 and 2 .
Answers
The mean-square end-to-end distance for the fractal line is ⟨R2⟩ = b².L^(1-D).
The mean-square end-to-end distance for the fractal line is as follows.⟨R2⟩ = ⟨(R(u)- R(v))^2⟩ for u = 0 and v = L where L is the length of the line.⟨R2⟩ = b²/L^2.D.L = b².L^(1-D).
Thus, the mean-square end-to-end distance for the fractal line is ⟨R2⟩ = b².L^(1-D).
The radius of gyration Rg is defined as follows.
Rg² = (1/N)∑_(i=1)^N▒〖(R(i)-R(mean))〗²where N is the number of monomers in the fractal line and R(i) is the position vector of the ith monomer.
R(mean) is the mean position vector of all monomers.
Since the fractal dimension is D, the number of monomers varies with the length of the line as follows.N ~ L^(D).
Therefore, the radius of gyration for the fractal line is Rg² = (1/L^D)∫_0^L▒〖(b/v^(1-D))^2 v dv〗 = b²/L^2.D(1-D). Thus, Rg² = b².L^(2-D).
The ratio R²/Rg² is given by R²/Rg² = L^(D-2).
When D = 1, R²/Rg² = 1/L. When D = 1.7, R²/Rg² = 1/L^0.7. When D = 2, R²/Rg² = 1/L.
This provides information on mean-square end-to-end distance and radius of gyration for fractal line with a given fractal dimension.
Learn more about mean-square from the given link
https://brainly.com/question/30763770
#SPJ11
F(x)=2x+4 translation 7 units left
Answers
F(x - 7)=2x - 10
Step-by-step explanation:
F(x)=2x+4 translation 7 units left is given as:
\(F(x - 7)=2(x - 7)+4 \\ \\ F(x - 7)=2x - 14+4 \\ \\ \purple{ \boxed{F(x - 7)=2x - 10 }} \\ \\ \)
in a random sample of 400 registered voters, 120 indicated they plan to vote for trump for president. determine a 95% confidence interval for the proportion of all the registered voters who will vote for trump.
Answers
The 95% confidence interval for the percentage of all eligible voters who intend to support Trump is (0.251, 0.349). If the true fraction does fall inside this range, we may say with 95% confidence.
We can use the following calculation to calculate a confidence interval for the percentage of all registered voters who intend to support Trump:
CI = p ± z\(\sqrt((p(1-p))/n)\)
where:
p is the proportion of the sample that will support Trump in the vote.
The critical value for the desired confidence level is z (95% confidence corresponds to a z-value of 1.96).
n is the sample size
When we enter the values from the issue, we get:
p = 120/400 = 0.3
z = 1.96
n = 400
CI = 0.3 ± 1.96sqrt((0.3(1-0.3))/400)
CI = 0.3 ± 0.049
CI = (0.251, 0.349)
Therefore, The 95% confidence interval for the percentage of all eligible voters who intend to support Trump is (0.251, 0.349). If the true fraction does fall inside this range, we may say with 95% confidence.
To learn more about confidence intervals, visit the link below:
https://brainly.com/question/29680703
#SPJ4
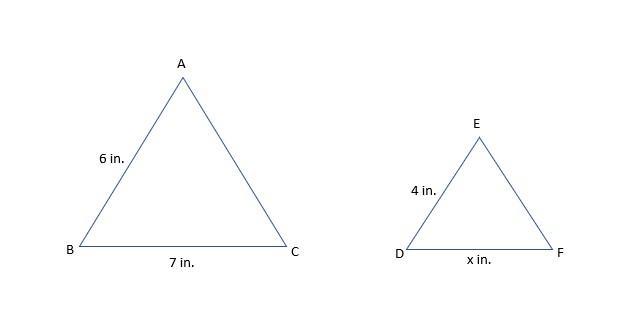
4. Triangle ABC is similar to triangle DEF. Which proportion must be true?
Answers
The similar triangles in the question, with proportional sides indicates;
4. The proportion that must be true is the option G
G. 4/6 = 7/x
What are similar triangles?Similar triangles are triangles are triangles that have the same shape but may have different sizes.
The possible triangles in the question includes two triangles with specified side lengths AB = 6 inches, AC = 7 inches, DE = 4 inches, DF = x inches
The definition of similar triangles indicates that we get;
DE/AB = EF/BC
DF/AC = DE/AB
DF/AC = EF/BC
Therefore;
(x/7) = 4/6
The correct option which indicates the proportion that must be true, therefore is option G
G. 4/6 = x/7
Part of the question includes two triangles, please see attached diagram created with MS Excel
The possible proportions, from which to select the proportion that must be true are;
F (7/x) = (4/6)
G 4/6 = x/7
H 6/4 = x/7
Learn more on similar triangles here: https://brainly.com/question/29782808
#SPJ1
6. Simplify: i) (a + b)(5a – 3b) + (a – 3b)(a – b) ii) (a – b) (a2 + b2 + ab) – (a + b) (a2 + b2 – ab) iii) (b2 – 49) (b + 7) + 343 okay, I know I posted this question before but, if you're giving your answers, please explain how you got it,
Answers
Answer:
Step-by-step explanation:
6. I will multiply then I respect the sign rules
- * - = +
- * + = -
I will atach the file immediately.
I multiplied the paranthesis and then I added the results
Answer:
i)6a^2-2ab-6b^2
ii)ab^2-1a^2b
iii)b^3-42b
Step-by-step explanation:
Use distributive property
Collect like terms
(a+b)(5a-3b)+(a-3b)(a-b)
(a+b)(5a-3b)---- Distributive property
5a^2-3ab+5ab-3b^2
5a^2+5ab-3ab-3b^2
5a^2+2ab-3b^2
(a-3b)(a-b)
a^2-ab-3ab-3b^2
a^2-4ab-3b^2
So,
5a^2+2ab-3b^2+a^2-4ab-3b^2---Collect like terms
5a^2+a^2+2ab-4ab-3b^2-3b^2
6a^2-2ab-6b^2
(a–b)(a^2+b^2 +ab)–(a + b)(a^2+b^2 –ab)
(a–b)(a^2+b^2 +ab)----Distributive property
a^3 since a^(1+2)=a^3
a^3+ab^2+a^2b-ba^2-b^3-ab^2
a^3+ab^2-ab^2+a^2b-ba^2-b^3
a^3+a^2b-a^2-b^3
a^3-b^3
(a+b)(a^2+b^2-ab)
a^3+ab^2-a^2b+ba^2+b^3-a^2b
a^3+ab^2+ba^2+b^3-a^2b-a^2b
a^3+ab^2+ba^2+b^3-2a^2b
So,
a^3-b^3-a^3+ab^2+ba^2+b^3-2a^2b--Collect like terms
a^3-a^3-b^3+b^3+ab^2-2a^2b+a^2b
ab^2-1a^2b
(b^2–49)(b + 7)+343---Distributive property
b^3+7b-49b-343+343---Collect like terms
b^3-49b+7b
b^3-42b
Hope this helps ;) ❤❤❤
Solve
|4t-8|=20
a
t=-3
b
t=-7
c
t=3
d
t=7
Answers
Answer:
a) t = -3
d) t = 7
Step-by-step explanation:
Given equation,
→ |4t - 8| = 20
Solving for the value of t,
→ |4t - 8| = 20
→ 4t - 8 = 20 || -4t + 8 = 20
→ 4t = 20 + 8 || -4t = 20 - 8
→ t = 28/4 || t = -(12/4)
→ [ t = 7 ] || [ t = -3 ]
Hence, value is 7 and -3.
its probably easy but i dont want to do my work

Answers
Answer:
1. 537.1
2. 8.15
3. 9.77
4. 26.75
Step-by-step explanation:
write an equation for a degree 6 polynomial with a root at 3, a double root at 2, and a triple root at -1, and has a y-int at 5..
Answers
The equation of the degree 6 polynomial with a root at 3, a double root at 2, and a triple root at -1, and y-intercept at y = 5 is given as follows:
y = -5/12(x - 3)(x - 2)²(x + 1)³.
How to define the polynomial?The equation of the function is obtained considering the Factor Theorem, as a product of the linear factors of the function.
The zeros of the function, along with their multiplicities, are given as follows:
Zero at x = 3 with a multiplicity of 1.Zero at x = 2 with a multiplicity of 2.Zero at x = -1 with a multiplicity of 3.Then the linear factors of the function are given as follows:
(x - 3).(x - 2)².(x + 1)³.The function is then defined as:
y = a(x - 3)(x - 2)²(x + 1)³.
In which a is the leading coefficient.
When x = 0, y = 5, due to the y-intercept, hence the leading coefficient a is obtained as follows:
5 = -12a
a = -5/12
Hence the polynomial is:
y = -5/12(x - 3)(x - 2)²(x + 1)³.
More can be learned about functions at https://brainly.com/question/24808124
#SPJ1
Find the future value of the annuity. payments of $5000 at the end of each year for 5 years at 5% interest compounded annually What is the future value of the annuity? (Round to the nearest cent.) Vie
Answers
The future value of the annuity is approximately $63814.06.
To find the future value of the annuity, we can use the formula for the future value of an ordinary annuity:
FV = P * [(1 + r)ⁿ⁻¹] / r
Where:
FV = Future value of the annuity
P = Payment amount per period ($5000)
r = Interest rate per period (5% or 0.05)
n = Number of periods (5 years)
Substituting the given values into the formula, we get:
FV = 5000 * [(1 + 0.05)⁵ - 1] / 0.05
Calculating the expression inside the brackets:
(1 + 0.05)⁵ - 1 = 1.27628125
Substituting this value back into the formula:
FV = 5000 * 1.27628125 / 0.05
FV ≈ $63814.06
Therefore, the future value of the annuity is approximately $63814.06.
To know more about future value:
https://brainly.com/question/33040220
#SPJ4
Jamal has 16 marbles. Zing has 9. How many fewer marbles does Zing
have than Jamal?
Answers
Answer:
7
Step-by-step explanation:
16 - 9 = 7
Answer:
7
Step-by-step explanation:
16-9=7
DhhdhcdchxKhkkjdchjcjjdhc
what are the correct answers?

Answers
cos (75)=cos (15) nothing square and check
Names jocelynn and i was wondering what is the name of the process of rewriting a quadratic equation so that one side is a perfect square trinomial?
i said completing the square but that was not it
Answers
The square is a useful technique in various mathematical applications, such as solving quadratic equations, the Vertex of a parabola, or converting a quadratic equation into vertex form
The process of rewriting a quadratic equation so that one side is a perfect square trinomial is indeed called "completing the square." It is a technique used to solve quadratic equations and also to convert them into a specific form that makes further manipulation easier.
Completing the square involves manipulating the quadratic equation by adding or subtracting a constant term in order to create a perfect square trinomial on one side of the equation. The goal is to express the quadratic equation in the form of (x + p)² = q, where p and q are constants.
The steps to complete the square for a quadratic equation in the form ax² + bx + c = 0 are as follows:
1. Divide the equation by the coefficient of x², so that the coefficient becomes 1.
2. Move the constant term (c) to the other side of the equation.
3. Add the square of half the coefficient of x to both sides of the equation.
4. Factor the perfect square trinomial on the left side of the equation.
5. Take the square root of both sides of the equation.
6. Solve for x by setting up two separate equations, one positive and one negative.
Completing the square is a useful technique in various mathematical applications, such as solving quadratic equations, finding the vertex of a parabola, or converting a quadratic equation into vertex form. It allows for easier analysis and simplification of quadratic expressions and helps in understanding the properties of quadratic functions.
In summary, completing the square is the name of the process used to rewrite a quadratic equation so that one side is a perfect square trinomial. It involves manipulating the equation to create a squared binomial expression, making it easier to solve or analyze the quadratic equation.
To know more about Vertex .
https://brainly.com/question/29476657
#SPJ8
Jayden's mass is 185kg, what is his weight?
Answers
Answer:
1814.85 N
Step-by-step explanation:
Weight = mass * acceleration of gravity
Jayden's weight = 185 * 9.81 = 1814.85 N
find the value of f(5) for each function. f(x) = 6 + 3x
Answers
Answer:
f(5) = 21
Step-by-step explanation:
Step 1: Define
f(x) = 6 + 3x
f(5) is x = 5
Step 2: Substitute and Evaluate
f(5) = 6 + 3(5)
f(5) = 6 + 15
f(5) = 21
A clock strikes once at one o'clock, twice at two o'clock, and so on. It also strikes once at half past each hour.
How many times altogether does this clock strike in 12 hours?!
Answers
-help me write an equation!!!

Answers
The absolute value function for this problem is given as follows:
g(x) = |x - 1| - 2.
How to define the absolute value function?An absolute value function of vertex (h,k) is defined as follows:
y = a|x - h| + k.
In which a is the leading coefficient.
The coordinates of the vertex for this problem are given as follows:
(1, -2).
As the slope of the line is of 1, the leading coefficient is given as follows:
a = 1.
Hence the absolute value function for this problem is given as follows:
g(x) = |x - 1| - 2.
More can be learned about absolute value functions at brainly.com/question/3381225
#SPJ1
If a = 2+ √5 and b = 1/a find a^2 + b^2
Answers
Hence, The Value of: a^2 + b^2 is 18
Step-by-step explanation: √ Find the RECIPROCAL of: ab = 1/a = 1/ 2 + √5
Rationalize the Denominator:b = 1/2 + √5 * 2 - √5/2 - √5
= 2 - √5/1
Simplify:b = 2 - √5
Square: A and B:a^2 = (2 + √5)^2 = 4 + 4√5 + 5
b^2 = (2 - √5)^2 = 4 - 4√5 + 5
ADD: a^2 and b^2:a^2 + b^2 = 4 + 4√5 + 5 + 4 - 4√5 + 5
= 18 - 3√5
So, Now we solve the Inverse property of addition: ±4 + 5 + 4 + 5
9 + 4 + 5
13 + 5 = 18
Move the expression to the right:a^2 + b^2 = 18
a^2 = 18 - b^2
Now we take the root of both sides/Negative/Positive:a = ± √18 - b^2
a = √18 - b^2
a = -√18 - b^2
Draw a conclusion:Hence, The Value of: a^2 + b^2 is 18
I hope this helps you!
Copy and complete: Two lines that do not intersect and are not coplanar are called__?
Answers
Answer: skew lines
Step-by-step explanation:
skew lines are two lines that do not intersect and are not coplanar
write down a system of first order differential equation that describe the behavior of x1, x2, x3 where xi denotes the ounces of salt in each tank
Answers
The system of first order differential equation are,
dx1/dt = -k1*x1 + k2*(x2-x1)
dx2/dt = k1*x1 - (k2+k3)*x2 + k4*(x3-x2)
dx3/dt = k3*x2 - k4*x3
To describe the behavior of x1, x2, and x3 (where xi denotes the ounces of salt in each tank) we can use a system of first order differential equations. Let's denote the rate of change of salt in each tank as dx1/dt, dx2/dt, and dx3/dt respectively.
Then, we can write the system of differential equations as:
dx1/dt = -k1*x1 + k2*(x2-x1)
dx2/dt = k1*x1 - (k2+k3)*x2 + k4*(x3-x2)
dx3/dt = k3*x2 - k4*x3
where k1, k2, k3, and k4 are constants that represent the rates of salt transfer between the tanks.
This system of first order differential equations describes how the ounces of salt in each tank change over time.
Learn more about "differential equation": https://brainly.com/question/1164377
#SPJ11
Aila wants to solve the equation -2.3 – 5x = 10 – 2x. She uses a graphing program to graph the equations y = -2.3 – 5x and y = 10 – 2x. Use the graph to find the solution of -2.3 – 5x = 10 – 2x. Line graph with 2 lines. X axis ranges from negative 10 to 10; y axis range from 6 to negative 6; both lines cross x, y axes; do not pass through origin; intersect at (negative 4.1, 18.2). Both lines extend from bottom right to upper left quadrants.
Answers
Answer:
-4.1
Step-by-step explanation: