An engineer wishes to determine the width of a particular electronic component. If she knows that the standard deviation of all components is 2.2 mm, how many of these components should she consider to be 80% sure of know the mean will be within 0.3 mm? Group of answer choices 1080 126 10 80 Way more than any of these answers
Answers
Answer:
The correct option is;
80
Step-by-step explanation:
The standard deviation of the components = 2.2 mm
The difference in the mean = 0.3
The level of confidence (power)= 80%
The formula for finding the sample size is given as follows;
\(n = \dfrac{2 \times \left [ (a + b)^2 \right ] \times \sigma ^2}{\left (\mu_1 - \mu_2\right )^2}\)
Where;
μ₁ - μ₂ = Is the difference in the mean = 0.3
a = The α multiplier = 0.05
b = The power multiplier = 0.8
σ = The standard deviation
n = The sample size
By substituting in the values, we have;
\(n = \dfrac{2 \times \left [ (0.05 + 0.8)^2 \right ] \times 2.2 ^2}{\left (2.2\right )^2} = 77.7\)
n ≈ 8
Rounding up to the next 10th gives;
n = 80
Therefore, the correct sample size should be about 80
Related Questions
Bob is quite proud of the 600-square-foot garage he’s included in his new home. According to national standards, how can he include the garage square footage in his total?
Answers
The method for including the garage square footage in the total depends on national standards, with some including it in the total and others excluding it.
When including the garage square footage in the total square footage of a home, there are different ways to do it depending on the national standards used.
Generally speaking, there are two main methods:
Including the garage in the total square footage, or excluding the garage from the total square footage.
If the garage is included in the total square footage, then Bob would add the square footage of the garage (600 square feet) to the square footage of the living spaces in the home (e.g., bedrooms, bathrooms, kitchen, living room, etc.).
This would give him the total square footage of the home, including the garage.
This method is commonly used in some areas of the United States.
On the other hand, if the garage is excluded from the total square footage, then Bob would only count the square footage of the living spaces in the home.
This method is commonly used in other areas of the United States, as well as in other countries.
It is important to note that the method used to calculate the total square footage can affect the perceived value of the home, as well as the taxes and insurance premiums associated with it.
Therefore, it is important for Bob to consult with a local real estate professional or appraiser to determine the most appropriate method for his area.
For similar question on national standards.
https://brainly.com/question/28455336
#SPJ11
A store buys 6 sweaters for $30 and sells them for $132. How much profit does the store make per sweater?
Answers
Answer:
$17
Step-by-step explanation:
$30/6- 5
$132/6-22
22-5
17
Two equal ide of a triangle are each 4m le than three time the third ide. Write down the dimenion of the triangle, if it perimeter i 55m
Answers
9 m, 23 m, and 23 m are the triangle's measurements.
What is meant by triangle's measurement?The total of a triangle's three inner angles is always 1800. Any two sides of a triangle can have a sum of lengths that is always greater than the length of the third side. Half of a triangle's area is equal to the sum of its base and height. Any triangle's three angles add up to a whole 180 degrees.Wisconsin University's Brian McCall A 45° 45° 90° triangle is a particular kind of isosceles right triangle in which the two legs are congruent and the non-right angles are both 45°. The hypotenuse or missing legs of 45 45 90 triangles can frequently be determined using the Pythagorean theorem.To learn more about triangle's measurement, refer to:
https://brainly.com/question/29611530
#SPJ4
which one is this? i need for a friend so they can help me

Answers
Answer:
The answer would be line AB
If l bisects (Line Over DE) at point R, DR = 2y + 9, and RE = 3y – 1, then find DE
Answers
Using the Bisector Theorem, the length of DE is 4y + 13 if we bisect (Line Over DE) at point R, DR = 2y + 9, and RE = 3y – 1.
Since l bisects DE at point R, we can use the segment bisector theorem, which states that the ratio of the lengths of the two segments is equal to the ratio of the lengths of the two other segments:
DR/RE = DE/ER
Substituting DR = 2y + 9 and RE = 3y - 1, we get:
(2y + 9)/(3y - 1) = DE/ER
Since R is the midpoint of DE, we have ER = DR = 2y + 9. Substituting this into the equation above, we get:
(2y + 9)/(3y - 1) = DE/(2y + 9)
Cross-multiplying, we get:
DE = (2y + 9)²/(3y - 1)
Expanding the numerator, we get:
DE = (4y² + 36y + 81)/(3y - 1)
Simplifying the expression, we get:
DE = 4y + 13
Learn more about bisector theorem at
https://brainly.com/question/10433817
#SPJ4
Un vendedor de celulaes tiene una meta diaria de venta si al momento lleva el Q.2,000.00 de la meta que equivale el 20%
Answers
Answer:
Sales goal, S = Q. 10,000
Step-by-step explanation:
Let the daily sales goal be S.Given the following data;
Amount sold = Q. 2,000.00Percentage of the sales goal = 20%To find his daily sales goal;
\( \frac {20}{100} * S = 2000 \)
\( 0.2 * S = 2000 \)
Dividing both sides by 0.2, we have;
\( S = \frac {2000}{0.2} \)
Sales goal, S = Q. 10,000
HELP PLEASE ILL GIVE 50 POINTS PLEASE DUE AT 11:59 WHERE I LIVE I HAVE AN HOUR!!!
i need a conclusion paragraph to the question - Was Abby Sunderland too young to sail solo? - SAYING THAT SHE WAS!
pleaseee the best conclusion will get brainliest!!!!!!!!!!
i am aware the subject is math accident
Answers
Answer:
Step-by-step explanation:
In conclusion, it can be argued that Abby Sunderland was too young to sail solo. Despite her ambitious and determined nature, her lack of experience and maturity put her at a significant risk during her solo sailing journey. The fact that she had to be rescued twice during her attempt highlights the dangers of attempting such a feat at such a young age. While it is admirable to have the courage to pursue one's dreams, it is important to consider the potential consequences and weigh them against the potential benefits. In this case, it can be argued that the risks far outweighed the potential rewards.
Please help me solve for X
I'll give brainlyest




Answers
Answer:
1. x = 8
2. x = 12
3. x = 11
4. x = 6
Step-by-step explanation:
1.
102 + 102 = 204
360 - 204 = 156
156 / 2 = 78
78 = 10x - 2
78 + 2 = 10x
80 = 10x
80 / 10 = x
x = 8
2.
81 = 7x - 3
81 + 3 = 7x
84 = 7x
84 / 7 = x
x = 12
3.
77 = 6x + 11
77 - 11 = 6x
66 = 6x
66 / 6 = x
x = 11
4.
115 + 115 = 230
360 - 230 = 130
130 / 2 = 65
65 = 8x + 17
65 - 17 = 8x
48 = 8x
48 / 8 = x
x = 6
SECTION A (20 MARKS) QUESTION 1 (a)Identify the relevant population for the below foci, and suggest the appropriate sampling design to investigate the issues, explaining why they are appropriate. Wherever necessary identify the sampling frame as well. 10 marks A public relations research department wants to investigate the initial reactions of heavy soft- drink users to a new all-natural soft drink'. (b) What type of sampling design is cluster sampling? What are the advantages and disadvantages of cluster sampling? Describe a situation where you would consider the use of cluster sampling. 10 marks
Answers
a) The relevant population is the heavy soft-drink users in the given case, and the appropriate sampling design that should be used is stratified random sampling. The list of all heavy soft-drink users is the sampling frame.
b) Cluster sampling refers to a sampling design where population is divided into naturally occurring groups and a random sample of clusters is chosen.
The advantages are efficient, easy to perform, and used when the population is widely dispersed. The disadvantages are sampling errors, have lower level of precision, and have the standard error of the estimate.
a) The relevant population for the public relations research department to investigate the initial reactions of heavy soft-drink users to a new all-natural soft drink is heavy soft-drink users. The appropriate sampling design that can be used to investigate the issues is stratified random sampling.
Stratified random sampling is a technique of sampling in which the entire population is divided into subgroups (or strata) based on a particular characteristic that the population shares. Then, simple random sampling is done from each stratum. Stratified random sampling is appropriate because it ensures that every member of the population has an equal chance of being selected.
Moreover, it ensures that every subgroup of the population is adequately represented, and reliable estimates can be made concerning the entire population. The list of all heavy soft-drink users can be the sampling frame.
b) Cluster sampling is a type of sampling design in which the population is divided into naturally occurring groups or clusters, and a random sample of clusters is chosen. The elements within each chosen cluster are then sampled.
The advantages of cluster sampling are:
Cluster sampling is an efficient method of sampling large populations. It is much cheaper than other types of sampling methods.Cluster sampling is relatively easy to perform compared to other methods of sampling, such as simple random sampling.Cluster sampling can be used when the population is widely dispersed, and it would be difficult to cover the entire population.The disadvantages of cluster sampling are:
Cluster sampling introduces sampling errors that could lead to biased results.Cluster sampling has a lower level of precision and accuracy compared to other types of sampling methods.Cluster sampling increases the standard error of the estimate, making it difficult to achieve the desired level of statistical significance.A situation where cluster sampling would be appropriate is in investigating the effects of a new medication on various groups of people. In this case, the population can be divided into different clinics, and a random sample of clinics can be selected. Then, all patients who meet the inclusion criteria from the selected clinics can be recruited for the study. This way, the study will be less expensive, and it will ensure that the sample is representative of the entire population.
Learn more about Stratified random sampling:
https://brainly.com/question/20544692
#SPJ11
Simplify the expression by combining like terms:
k3+ m + m - k3 +Ka+ K2
Answers
Explanation:
k3 + m + m - k3 + Ka + K2
= 2m + Ka + K2
Dave dropped an object partway up his rock climb. If the object took exactly 2 seconds to hit the ground how high did he climb?
Write a quadratic formula and solve.
Answers
Dave climbed to a height of 4 meters before dropping the object. Note that this assumes that Dave dropped the object straight down and did not throw it horizontally. If he threw it horizontally, then the calculation would be more complicated and would require additional information.
We can use the kinematic equation for vertical motion under constant acceleration due to gravity to solve this problem:
y = yo + voy*t + 1/2*a*t^2
where y is the final height, yo is the initial height (in this case, the height where Dave dropped the object), voy is the initial velocity (which is zero), a is the acceleration due to gravity (-9.8 m/s^2), and t is the time it takes for the object to hit the ground (2 seconds).
Substituting the given values into the equation, we get:
y = yo + 1/2*a*t^2
y = yo + 1/2*(-9.8 m/s^2)*(2 s)^2
y = yo + 19.6 m
Therefore, the height that Dave climbed is equal to the initial height of the object plus 19.6 meters.
To solve for the initial height, we would need more information. However, we can set up a quadratic equation to represent the problem:
-4.9h^2 = -19.6h
where h is the initial height in meters. We can simplify this equation by dividing both sides by -h:
4.9h = 19.6
Solving for h, we get:
h = 4 meters
To learn more about equation visit:
brainly.com/question/10413253
#SPJ11
Find the value of x. Round to the
nearest tenth.
26
12
X
X = [?]
![Find the value of x. Round to thenearest tenth.2612XX = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/Ou7DgfLpEtRbbjMNMDRMd0ZMD81Ra7kN.png)
Answers
Answer:
y = 4x - 2
y = -x + 3
Step-by-step explanation:
The area of a rectangle is 36 units^2
The length is 9, and the width is Va.
What is the value of x?
What is the width of the rectangle?
Answers
Answer:
The width is 4
Step-by-step explanation:
the length times the with is the area
since the area is 36
9 times x = 36
so
since 9 x 4 = 36,
the width is 4
Find sin20 if sin 0 = 3; 90° < 0 < 180°
Answers
Answer:
\(\sin 2 \theta = -\dfrac{4\sqrt 5}{9}\)
Step-by-step explanation:
\(\text{Given that,}\\\\~~~~~~\sin \theta = \dfrac 23\\\\\implies \sin^2 \theta = \left( \dfrac 23 \right)^2\\\\\implies 1- \cos^2 \theta = \dfrac 49 \\\\\implies \cos^2 \theta = 1 - \dfrac 49 \\\\\implies \cos^2 \theta = \dfrac 59\\\\\implies \cos \theta = \pm\sqrt{\dfrac 59} \\\\\implies \cos \theta = \pm \dfrac{\sqrt 5 }3\\\\\text{Since}~ 90^\circ < \theta < 180^{\circ},~\text{the angle lies in 2nd quadrant}\left(\cos \theta ~\text{is negative}\right).\\\\\)
\(\text{So,}~ \cos \theta = - \dfrac{\sqrt 5 }{3}\\\\\text{Now,}\\\\\sin 2\theta = 2\sin \theta \cos \theta \\\\\\~~~~~~~~=2 \cdot \dfrac 23 \cdot \left( -\dfrac{\sqrt 5}{3} \right)\\\\\\~~~~~~~~=-\dfrac{4\sqrt 5}{9}\)
\(\textbf{Quadrant rule:}\\\\\)

On what interval is the graph increasing?
On what interval is the graph decreasing?
Does the graph have a relative maximum or relative minimum? If so, what is it?
Points -
(-3,-2)
(-2,0)
(-1,2)
(0,4)
(1,2)
(2,0)
(3,-2)

Answers
The answer is, On the interval (-3,-2) to (0,4), is the graph increasing.
On (0,4) to (3,-2) interval is the graph decreasing.
the graph have a relative maximum at (0,4).
What is graph?In mathematics, the graph of a function f is the set of ordered pairs, where {\displaystyle f(x)=y.} In the common case where x and f(x) are real numbers, these pairs are Cartesian coordinates of points in two-dimensional space and thus form a subset of this plane.
here, we have,
from the given graph we get,
On the interval (-3,-2) to (0,4), is the graph increasing.
On (0,4) to (3,-2) interval is the graph decreasing.
the graph have a relative maximum at (0,4).
To learn more on graph click:
brainly.com/question/17267403
#SPJ1

Enter your answer and show all the steps that you use to solve this problem in the space provided.
write an expression for the area of the shaded region in its simplest form. show all of your steps.
Answers
The area of the shaded region in its simplest form x^2 +23x +49
First, we find the area of the rectangle as though the small square was not cut out of it
A = (x+10) (2x+5)
Foil
2x^2 +5x+20x+50
2x^2 +25x+50
Then we find the area of the small square
A = (x+1) (x+1)
FOIL
x^2 +x+x+1
x^2 +2x+1
Then we subtract the small square from the large rectangle to find the area of the shaded region
2x^2 +25x+50 - (x^2 +2x+1)
Distribute the minus sign
2x^2 +25x+50 - x^2 -2x-1
x^2 +23x +49
Know more about equations at:
brainly.com/question/26310043
#SPJ4
Hey Guys! I have so good answers. I still have no brainliests. If I answer your question, and if its correct, please mark me brainliest. You get points if you respond to this question; 10 points.
Answers
I want to give a Brainliest to you. Friends??
a sphere of radius r inches is sliced by a plane that is d inches from the center. in terms of r and d, what is the radius of the circle of intersection?
Answers
The cross-sectional area will be π*(y^2-x^2) as area of a circle with radius r is π*r^2.
What is equations?There are many different ways to define an equation.The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions.For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign. Mathematical algebraic equations typically have one or more variables.A linear equation may have more than one variable. A linear equation is an equation in which the highest power of the variable is always 1.This is a second-order equation. In quadratic equations, at least one of the variables should be raised to exponent 2.Hence, The cross-sectional area will be π*(y^2-x^2) as area of a circle with radius r is π*r^2.
learn more about equations click here:
brainly.com/question/25976025
#SPJ4
prove or disprove: if proju(v) = proju(w) then (v − w) ⊥ u.
Answers
Therefore, (v - w) is orthogonal to u, which implies that the statement "if proju(v) = proju(w) then (v − w) ⊥ u" is true.
How the statement "if proju(v) = proju(w) then (v − w) ⊥ u" is true?The statement "if proju(v) = proju(w) then (v − w) ⊥ u" is true if and only if u is orthogonal to the projection of (v-w) onto the subspace spanned by u.
Assume that proju(v) = proju(w)Since proju(v) and proju(w) are the projections of v and w onto the subspace spanned by u, we can rewrite the statement as "if the projections of v and w onto the subspace spanned by u are equal, then (v - w) is orthogonal to u".
Prove that (v - w) is orthogonal to u if and only if the projection of (v - w) onto the subspace spanned by u is the zero vector.Let proj_u(v - w) be the projection of (v - w) onto the subspace spanned by u. We know that (v - w) can be decomposed as (v - w) = proj_u(v - w) + (v - w - proju(v - w)).
Note that (v - w - proju(v - w)) is orthogonal to the subspace spanned by u, since proju(v - w) is the closest vector in the subspace to (v - w). Therefore, (v - w) is orthogonal to u if and only if proju(v - w) = 0, which is equivalent to saying that the projection of (v - w) onto the subspace spanned by u is the zero vector.
Use the above result to prove or disprove the statement.Assuming that proju(v) = proju(w), we have:
proju(v - w) = proju(v) - proju(w) = proju(v) - proju(w) = 0
Therefore, (v - w) is orthogonal to u, which implies that the statement "if proju(v) = proju(w) then (v − w) ⊥ u" is true.
In conclusion, we have proven that if the projections of v and w onto the subspace spanned by u are equal, then (v - w) is orthogonal to u.
Learn more about orthogonal
brainly.com/question/2292926
#SPJ11
The tables show the attendances at volleyball games and basketball games at a school during the year.
Express the difference in the measures of center as a multiple of the measure of variation. Round your answers to the nearest tenth.
The difference in the means is about (blank) to (blank) times the MAD.
Solve for blanks
Answers
a) Compare the populations using measures of center and variation. Mean and MAD of vollyball game attendence are 86, 19.6 respectively. Mean and MAD of basketball game attendence are 185, 17.7 respectively.
b) Difference in the measures of center as a -4.6 to 5.1 multiple of the measure of variation. The difference in the means is about -4.6 to 5.1 times the MAD.
We have two tables consists attendances at volleyball games and basketball games at a school during the year. See the above figure carefully. Now, Compare the populations using measures of center and variation : As we know mean of data is calculated by dividing the sum of data values to the number of data values. Here, Sum of vollyball attendence values, ∑xᵢ = 1720
Number of days = 20
So, mean of vollyball game attendence
= 1720/20 = 86
Sum of basketball ball attendence values, ∑yᵢ = 3700
Number of days = 20
So, mean of basketball ball game attendence = 3700/20 = 185
Now, measure absolute deviations, MAD
MAD of vollyball game attendence is
= [∑( mean of vollyball game attendence - attendance values (i))]/number of days
= 392/20 = 19.6
MAD of basketball ball game attendence is = [∑( mean of basketball ball game attendence - attendance values (i))]/number of days
= 354/20 = 17.7
b) Now, we check the relation between difference in the measures of center as a multiple of the measure of variation.
A : vollyball game attendence
B : basketball game attendence
difference in the measures of center
= Mean (A) - Mean(B) or Mean(B) - Mean (A)
measure of variation, MAD(A) , MAD(B)
[Mean (A) - Mean (B)]/MAD(A)
= ( 86 - 185)/19.6
= -4.643 ~ -4.6
[Mean (B) - Mean (A)]/MAD(B)
= ( 185 - 86)/17.7
= 91/17.7 = 5.1412 ~ 5.1
Hence, difference in the means is about -4.6 to
5.1 times the MAD.
For more information about Measure of variance, visit :
https://brainly.com/question/28420527
#SPJ4
Complete question :
The above tables show the attendances at volleyball games and basketball games at a school during the year. Volleyball Game Attendance Basketball Game Attendance 112 95 84106 62 68 75 88 93 127 98 117 60176 141 152 181 198 21 49 5485 74 88 132 5 202 190 173 155 169 188 195 4 179 163 186 184207 219 228
a) Compare the populations using measures of center and variation.
b) Express the difference in the measures of center as a multiple of the measure of variation. Round your answers to the nearest tenth. The difference in the means is about (blank) to (blank) times the MAD.


How long would it take R20000 invested today at a simple interest rate of 9% p.a. to reach an investment goal of R30000.
A Approximately 5.6 years
B Approximately 6.1 years
C Approximately 4.7 years
D Approximately 5.1 years
Answers
\(~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 30000\\ P=\textit{original amount deposited}\dotfill & \$20000\\ r=rate\to 9\%\to \frac{9}{100}\dotfill &0.09\\ t=years \end{cases} \\\\\\ 30000 = 20000[1+(0.09)(t)] \implies \cfrac{30000}{20000}=1+0.09t\implies \cfrac{3}{2}=1+0.09t \\\\\\ \cfrac{3}{2}-1=0.09t\implies \cfrac{1}{2}=0.09t\implies \cfrac{1}{2(0.09)}=t\implies 5.6\approx t\)
somebody please help im giving 20 points and a brainliest !

Answers
Answer:
Initial is $26000
It's representing decay.
9.1% change each year.
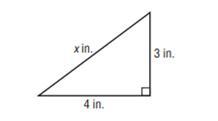
course 3 chapter 5 triangles and the pythagorean theorem answer key
Answers
In the given right triangle, the perimeter is 12 in.
According to the Pythagorean theorem, in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the length of the two legs (a and b). Hence,
c^2 = a^2 + b^2
In the given triangle,
c = x in
a = 3 in
b = 4 in
Hence,
x^2 = 3^2 + 4^2
x^2 = 9 + 16
x^2 = 25
x = √25
x = 5
The perimeter of a geometric shape is the sum of all its side. Hence,
Perimeter = 3 + 4 + 5 = 12 in
Note: The question is incomplete. The complete question probability is: Using the Pythagorean theorem, find the perimeter of the triangle.
Learn more about Pythagorean theorem:
https://brainly.com/question/28981380
#SPJ4
Identify whether the function graphed has na odd or even degree and a positive are negative leading cooefficient

Answers
To determine if the degree of the function is odd or even we need to look at the extrema of the graph. If both points to the same side, it is, if X goes to positive infinity or to negative infinity, to both direction Y of the graph is going to the same direction, it means that the degree os even. Otherwise, when the extrema are pointing in different directions, it means the degree is odd.
In the present graph, the degree is odd, because the graph has different directions for each extrema.
To determine the signal to the leading coeficient, we check the direction Y is going to increasing values of X. If Y goes positive, the leading coeficient is positive, if it is negative, the leading coeficiente is negative.
In the present graph, the leading coeficient is positive, because for increasing values of X we have increasi
I WILL GIVE BRAINLIEST!!!!!!
Write in complete sentences to explain what a budget is, how to make one, and how to balance it.
Answers
Write and solve an inequality that represents the values of x, in feet.
The perimeter is less than 16 feet.
Answers
Answer:
x < 16 ft
Step-by-step explanation:
Perimeter = x
If it is less than 16, the equation is:
x < 16
-Chetan K
Mathematics, Probability question

Answers
Answer: 2 is the probability i think
Given that D(x) = 2x, select all of the following that are true statements.
D( x) is a direct variation.
O D( x) is a function.
D( X) is a rule for the set of points (5, 10), (6, 12) and (-2,-4).
O xls the dependent variable.
D(6) = 3
Answers
You welcome
what is the smallest positive integer which when divided by 4, 5, 8 and 9 leaves remainder 3, 4, 7 and 8, respectively?
Answers
X = 40c + 39 = 40(4) + 39 = 199 is the required smallest positive integer.
The smallest positive integer which when divided by 4, 5, 8 and 9 leaves remainder 3, 4, 7 and 8, respectively is 539.
The given equation isx ≡ 3 (mod 4)x ≡ 4 (mod 5)x ≡ 7 (mod 8)x ≡ 8 (mod 9)
By the first condition,x = 4a + 3
where a is any positive integer.
Substituting in the second condition,4a + 3 ≡ 4 (mod 5)⇒ 4a ≡ 1 (mod 5)⇒ a ≡ 4 (mod 5)
Let a = 5b + 4 (where b is any positive integer)
Substituting this in x = 4a + 3, we get
x = 4(5b + 4) + 3 ⇒ x = 20b + 19
Now, substituting this in the third condition,20b + 19 ≡ 7 (mod 8)⇒ 4b ≡ 4 (mod 8)⇒ b ≡ 1 (mod 2)Let b = 2c + 1
Substituting this in x = 20b + 19,x = 20(2c + 1) + 19 ⇒ x = 40c + 39
Finally, substituting this in the fourth condition,40c + 39 ≡ 8 (mod 9)⇒ 4c ≡ 5 (mod 9)
We know that the modular inverse of 4 modulo 9 is 7.
Multiplying both sides by 7,7(4c) ≡ 7(5) (mod 9)⇒ 28c ≡ 35 (mod 9)⇒ c ≡ 4 (mod 9)
Hence,x = 40c + 39 = 40(4) + 39 = 199 is the required smallest positive integer.
for such more question on integer
https://brainly.com/question/929808
#SPJ11
if 1 and -3 are the zeroes of the polynomial xcube - axsquare - 13x + b find the values of a and b
Answers
Step-by-step explanation:
f(x) = x³ - ax² - 13x + b.
f(1) = 1³ - a(1)² - 13(1) + b = 0
=> 1 - a - 13 + b = 0, b - a - 12 = 0.
f(-3) = (-3)³ - a(-3)² - 13(-3) + b = 0
=> - 27 - 9a + 39 + b = 0, 12 - 9a + b = 0.
Therefore, b - a - 12 = 12 - 9a + b. 8a = 24, a = 3.
=> b - (3) - 12 = 0, b = 15.