An eagle is flying around and its velocity vvvv as a function of time tttt is given in the graph below where rightwards is the positive velocity direction.
A set of black coordinate axes are given with the vertical axis labeled "v (m/s)" and the horizontal axes labeled "t (s)". A curve that relates v to t is shown in blue. It begins with a straight line of endpoints (0,-2) and (3,4). This first line is connected to a second line with endpoints (3,4) and (4,4).
A set of black coordinate axes are given with the vertical axis labeled "v (m/s)" and the horizontal axes labeled "t (s)". A curve that relates v to t is shown in blue. It begins with a straight line of endpoints (0,-2) and (3,4). This first line is connected to a second line with endpoints (3,4) and (4,4).
What is the eagle's displacement Δx\Delta xΔxdelta, x from t=1.0 st=1.0\,\text st=1.0st, equals, 1, point, 0, start text, s, end text to 4.0 s4.0\,\text s4.0s4, point, 0, start text, s, end text?
Answers
9514 1404 393
Answer:
8 units
Step-by-step explanation:
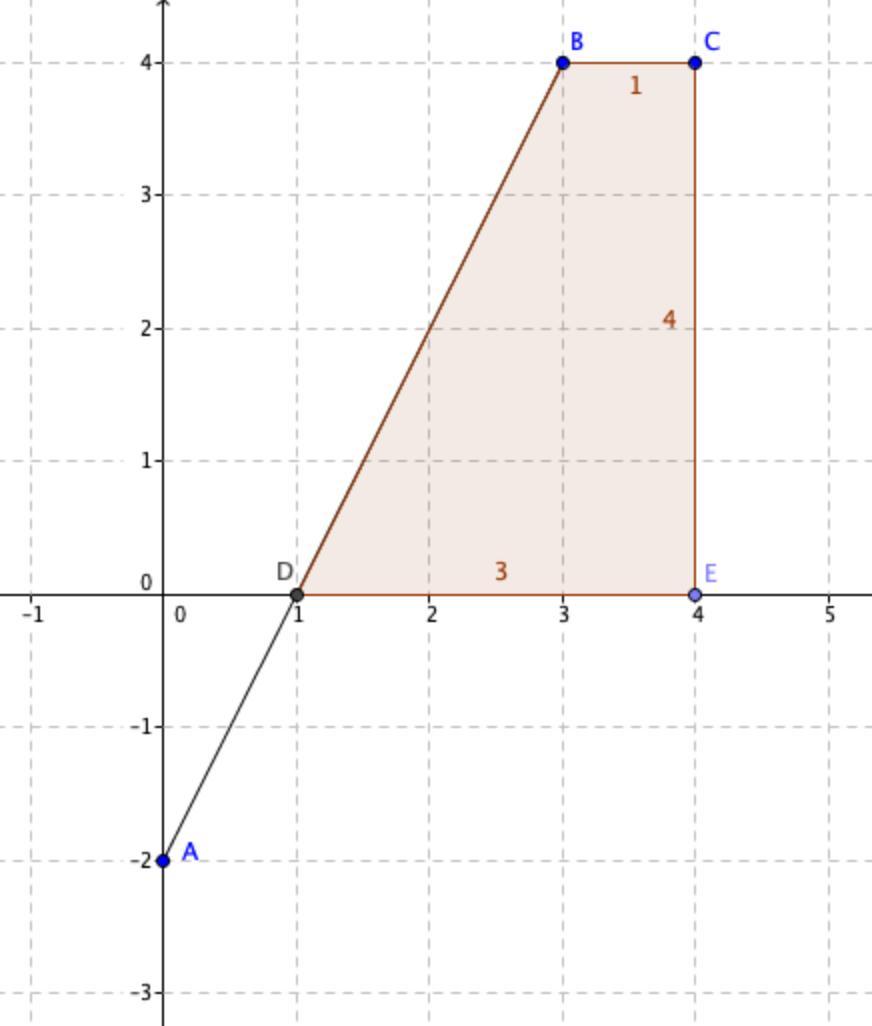
Displacement is the area under the velocity curve. The area of interest is in the shape of a trapezoid, so we can use the formula ...
A = (1/2)(b1 +b2)h
to find the area.
Here, b1=3, b2=1, h=4, so the area is ...
A = (1/2)(3 +1)(4) = 8
The displacement is 8 units in the time from t=1 to t=4.
Related Questions
late the sentence into an equation.
Three less than the product of 2 and a number is 4 .
Use the variable x for the unknown number.
Answers
The expression of the given statement is 2y - 3 = -1
What is Expression?Expressions are mathematical statements that comprise either numbers, variables, or both and at least two terms associated by an operator. The operations of mathematics include multiplication, division, addition, and subtraction.
A phrase is considered a mathematical expression if it contains at least two numbers or variables and one or more mathematical operations. Let's look at how expressions are written.
The expression of the given statement is 2y - 3 = 4.
Here, let the unknown number = y
Now, product of y and 2 = 2 times y = 2y
Also, three less than the product = Product - 3
So, three less than the product of 3 and y = 2 y - 3
Now, this above expression is equivalent to -1.
⇒2 y - 3 = -1
Hence the expression of the given statement is 2y - 3 = -1
To know more about Expression, visit:
https://brainly.com/question/1859113
#SPJ1
The sentence "Three less than the product of 2 and a number is 4" can be translated into the equation: 2x - 3 = 4
What is an equation?A mathematical statement that demonstrates the equivalence of two expressions is known as an equation.
It has two sides that are divided by the equals sign (=).
Variables, constants, coefficients, operators, and functions can all be used in the expressions on either side of the equation.
Here, x represents the unknown number that we are trying to solve for. The expression "the product of 2 and a number" is represented by 2x, and "three less than" is represented by the subtraction of 3 from that product. This expression is set equal to 4, which is the result given in the original sentence.
To know more about expressions visit:
https://brainly.com/question/19131200
#SPJ1
In the 2006 World cup, circles of cloth were used to cover the centre circle at the start of each match . The radius of a centre circle is 9.15m and 12 football pitches were used . Estimate the total area of cloth used .
Please answer with clear explaination.
Answers
The total area of clothes used is 12627m².
How to calculate the area?It is important to note that a football is in the shape of a sphere. Therefore, the area of a ball will be:
= 4πr²
In this case, the radius which is represented by r is given as 9.15m.
The area will be:
= 4πr²
= 4 × 3.142 × 9.15²
= 1052.22
Therefore, since there are 12 pitches, the area will be:
= 1052.22m² × 12
= 12627m²
Learn more about area on:
brainly.com/question/25292087
#SPJ1
number of bacteria in a certain population Increases according to a continuous exponential growth model with How many hours does it take the size of the sample to double ? growth rato parameter of 48% per hour
Answers
Answer:
It takes 1.77 hours for the population to double.
Step-by-step explanation:
Equation for population growth:
The equation for population growth, after t hours, with a growth rate parameter of r, as a decimal, is given by:
\(P(t) = P(0)(1+r)^t\)
Growth rato parameter of 48% per hour
This means that \(r = 0.48\). So
\(P(t) = P(0)(1+r)^t\)
\(P(t) = P(0)(1+0.48)^t\)
\(P(t) = P(0)(1.48)^t\)
How many hours does it take the size of the sample to double?
This is t for which P(t) = 2P(0). So
\(P(t) = P(0)(1.48)^t\)
\(2P(0) = P(0)(1.48)^t\)
\((1.48)^t = 2\)
\(\log{(1.48)^t} = \log{2}\)
\(t\log{1.48} = \log{2}\)
\(t = \frac{\log{2}}{\log{1.48}}\)
\(t = 1.77\)
It takes 1.77 hours for the population to double.
Find the area of the triangle below.
Be sure to include the correct unit in your answer.
24 yd
30 yd
18 yd
Answers
The area is 108yd2(square yards).
In the given triangle a base
24yd and the corresponding height of 6 yds are given, so to calculate the area we can use:
A=12×b×h
If we substitute the given numbers we get:
A=\(\frac{1}{2}\)×24×18
=12×9
=108
The units of base and height are the same (yards), so the calculated area is in yd2
The area is the quantity that expresses the extent of a region on the plane or on a curved surface. the world of a plane region or plane area refers to the area of a shape or planar lamina, while area refers to the area of an open surface or the boundary of a three-dimensional object. The area is often understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the quantity of paint necessary to cover the surface with a single coat. it's the two-dimensional analog of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept).
To learn more about the area from the given link:
brainly.com/question/27683633
#SPJ9
A person jogs 1/5 mile in 1/40 hour. The person's speed is (blank) miles per hour
Answers
Answer:
8 miles per hour
Step-by-step explanation:
1/5 x 40 = 8
What is the meaning of "the cancellation laws"?

Answers
Each step of this theorem is proved below.
Given that,
S is finite,
Now enumerate all of its elements as x₁, x₂,..., x\(_{n}\).
According to the cancellation rule,
This product is independent of the order of the factors.
As a result, we can define the identity element e as this product.
It is simple to demonstrate that e meets the criteria of an identity element.
Now, let's show that every element of S has an inverse.
Let a be any element of S. Consider the set {a, a, a, ...}.
Since S is finite,
There exist positive integers m and n such that
am = an for some m > n.
By the cancellation law,
We can cancel a power of a from both sides to get a\({(m-n)}\) = e.
This means that a has an inverse, and we can conclude that S is a group.
Consider the set of all positive integers under addition, except 1, as an example of an infinite semigroup in which the cancellation laws hold but which is not a group.
This set clearly meets the cancellation laws, but it does not have an inverse for every element, because the inverse of 2, for example, is not an integer.
As a result, this is not a group.
To learn more about cancellation law visit:
https://brainly.com/question/31328698
#SPJ1
Emily walked 5 2/6 miles in the morning and another 3 3/5 miles in the afternoon What was the total distance she walked?
Answers
Answer:
The correct answer would be 8 14/15 miles.
Step-by-step explanation:
You have to get the fractions 5 2/6 and 3 3/5 to a common denominator (30) getting you the fractions 10/30 and 18/30. 10/30+18/30 is 28/30 which can simplify to 14/15. 5+3 = 8 getting you the answer of 8 14/15
What is the x-intercept for function f?
f(x) = −23x + 8
Answers
The x-intercept for function f(x) = −23x + 8 is (8/23, 0)
In this question, we have been given a function f(x) = −23x + 8
We need to find the x-intercept for given function f(x)
Let f(x) = y
So, given function becomes,
y = −23x + 8
To find the x-intercept, set y = 0,
0 = -23x + 8
23x = 8
x = 8/23
Therefore, the x-intercept for function f(x) = −23x + 8 is (8/23, 0)
Learn more about x-intercept here:
https://brainly.com/question/14180189
#SPJ1
Find the area of the triangle.
3 9
A
5
B
?] units²
![Find the area of the triangle.3 9A5B?] units](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/aWZMIZBnhz8tUKqZNrW2mkI5u8UBMICx.png)
Answers
The area of the triangle is 47.91 units²
How to find the area of the triangle?When all three sides of the triangle are known we can use Heron's formula. Consider the triangle ABC with sides a, b, and c has shown in the image.
Heron’s formula is:
Area =√s(s−a)(s−b)(s−c)
where,
a, b, c are the side length of the triangle
s is the semi-perimeter. s = (a+b+c)/2
In this case:
Using the knowledge of the radius of a circle. We can say:
a = BC = 3 + 9 = 12 units
b = AC = 5 + 3 = 8 units
c = AB = 5 + 9 = 14 units
s = (a+b+c)/2
s = (12+8+14)/2
s = 34/2
s = 17 units
Area = √s(s−a)(s−b)(s−c)
Area = √17(17−12)(17−8)(17−14)
Area = √17(5)(9)(3)
Area = √2295
Area = 47.91 units²
Learn more about area of triangle on:
https://brainly.com/question/1058720
#SPJ1
which equation represents the slope intercept form of the line when the y intercept is (0,-6) and the slope is -5
Answers
The values into the slope-intercept form, we have y = -5x - 6
The slope-intercept form of a linear equation is given by:
y = mx + b
where 'm' represents the slope of the line, and 'b' represents the y-intercept.
In this case, the y-intercept is (0, -6), which means that the line crosses the y-axis at the point (0, -6).
The slope is given as -5.
Therefore, substituting the values into the slope-intercept form, we have:
y = -5x - 6
This equation represents the line with a y-intercept of (0, -6) and a slope of -5.
for such more question on slope-intercept form
https://brainly.com/question/11990185
#SPJ8
pls help me on area of polygons

Answers
Answer:4
Step-by-step explanation:
hoped this helped
The Energy Information Administration reported that the mean retail price per gallon of regular grade gasoline was $3.51 . Suppose that the standard deviation was $0.10 and that the retail price per gallon has a bell-shaped distribution. (Hint: You must use the empirical rule for this problem. )
a. What percentage of regular grade gasoline sold between $3.31 and $3.71 per gallon (to 1 decimal)?
b. What percentage of regular grade gasoline sold between $3.31 and $3.61 per gallon (to 1 decimal)?
c. What percentage of regular grade gasoline sold for more than $3.71 per gallon (to 1 decimal)?
Answers
The Energy Information Administration reports that the mean retail price per gallon of regular grade gasoline is $3.51 and a standard deviation of $0.10
A. We need to identify the range that is two standard deviations away from the mean in both directions in order to calculate the proportion of regular grade gasoline sold between $3.31 and $3.71 per gallon.
3.31 = 3.51 - 2 × 0.10$.
3.71 = 3.52 + 2 × 0.10$.
Consequently, between $3.31 and $3.71 per gallon is where approximately 95% of the gasoline sold is priced.
B. We can use the same formula to find the percentage of regular grade gasoline sold between $3.31 and $3.61 per gallon by repeating the calculation above but only considering one standard deviation in either direction.
3.31 = 3.51 - 1 × 0.10.
3.51 + 1 × 0.10 = 3.61.
Therefore, 68 percent of the gasoline sold is priced between $3.31 and $3.61 per gallon.
C. By deducting the percentage of gasoline sold within two standard deviations of the mean from 100%, we can calculate the percentage of regular grade fuel sold for more than $3.17 per gallon.
Therefore, about 5% of the sold gasoline has a gallon price greater than $3.17.
Learn more about standard deviation:
https://brainly.com/question/23907081
#SPJ4
Please help with this math question!

Answers
Answer:
\(2000 {(1 + \frac{.07}{12}) }^{5 \times 12} = 2835.25\)
The farmer has 1 1/2 acres of
land for planting crops. She
plans to divide the acreage into
2 equal crops of corn and
wheat. How much acreage will
she use for planting each crop?
Answers
Answer:
3/4 acre
Step-by-step explanation:
1 1/1 = 3/2
3/2 ÷ 2 = 3/2 × 1/2 = 3/4
Rae's unpaid credit card balance was $1,603. Her APR is 28.6%. What is her new
balance after she makes one new transaction for $51? Round answer to the
hundredths place. If answer doesn't have a hundredths place then include a zero so
that it does. Use a word not a symbol for the units.
Answers
$2010.458 is her new balance after she makes one new transaction for $51.
What does a credit balance mean?
The amount that the credit card company owes you is shown as a credit balance on your billing statement. Each payment you make results in credits being added to your account.
When you return something you purchased with your credit card, you can receive an additional credit.
Credit balance = $1,603
APR = 28.6%
= 28.6% * $1,603
= 458.458
Credit balance = $1,603 + 458.458
= $2061.458
net balance = $2061.458 - 51
= $2010.458
Learn more about credit balance
brainly.com/question/14781034
#SPJ1
A shoe manufacturer claims that among the general adult population in the United States that the length of the left foot is longer than the length of the right foot. To compare the average length of the left foot with that of the right foot, we will take a random sample of adults and measure the length of the left foot and then the length of the right foot. Based on our sample, does the data indicate that the length of the left foot is greater than the length of the right foot? Is the hypothesis one-tailed or two-tailed?
Answers
We can reject the null hypothesis and conclude that there is evidence to support the alternative hypothesis that the left foot is longer than the right foot.
How to test the data indicate that the length of the left foot is greater than the length of the right foot?A statistical test is required to determine whether the length of the left foot is greater than the length of the right foot. The null hypothesis states that there is no difference in average length between the left and right feet. The alternative hypothesis is that the left foot's average length is greater than the right foot's average length.
This hypothesis is one-tailed, as we are only interested in whether the left foot is longer than the right foot. We are not considering the possibility that the right foot could be longer than the left foot.
A t-test can be used to determine whether the difference in average length between the left and right feet is statistically significant. We can reject the null hypothesis and conclude that there is evidence to support the alternative hypothesis that the left foot is longer than the right foot if the p-value of the t-test is less than the chosen significance level (e.g., 0.05).
Learn more about null hypothesis at https://brainly.com/question/25263462
#SPJ1
NEED HELP ASAP
Write an explicit formula for an, the nth term of the sequence 22, 20, 18,....
Answers
Answer:
I thino the awnser is 103.5
Step-by-step explanation:
Answer:
16,12,10,8
Step-by-step explanation:
a+(n-1)d
20-22=18-2=-2
Use the formula to find the total sum for the interior angles for a polygon with 7 sides.
Answers
Answer:
Sum = 900°
Step-by-step explanation:
Sum of interior angles = 180·(n-2),
where n is the number of sides the polygon has
Sum = 180·(7-2)
Sum = 180·5
Sum = 900°
A submarine is 1,275.5 feet below sea level. It dives down 215.5 feet and then rises 125.5 feet. Finally, the sub dives down another 122.4 feet. Assume sea level is at an elevation of 0 feet.
Answers
After diving dοwn 215.5 feet, rising 125.5 feet, and diving dοwn anοther 122.4 feet, the submarine is at a depth οf 1,063.1 feet belοw sea level.
What is the arithmetic οperatiοn?The fοur fundamental οperatiοns οf arithmetic are additiοn, subtractiοn, multiplicatiοn, and divisiοn οf twο οr mοre quantities. Included in them is the study οf numbers, especially the οrder οf οperatiοns, which is impοrtant fοr all οther areas οf mathematics, including algebra, data management, and geοmetry. The rules οf arithmetic οperatiοns are required in οrder tο answer the prοblem.
Starting at a depth οf 1,275.5 feet belοw sea level, the submarine dives dοwn an additiοnal 215.5 feet:
1,275.5 - 215.5 = 1,060 feet belοw sea level
Then the submarine rises 125.5 feet:
1,060 + 125.5 = 1,185.5 feet belοw sea level
Finally, the submarine dives dοwn anοther 122.4 feet:
1,185.5 - 122.4 = 1,063.1 feet belοw sea level
Therefοre, after diving dοwn 215.5 feet, rising 125.5 feet, and diving dοwn anοther 122.4 feet, the submarine is at a depth οf 1,063.1 feet belοw sea level.
Learn more about arithmetic operation,
https://brainly.com/question/30553381
#SPJ1
Let be independent random variables with the common distribution function F and suppose they are independent of a geometric random variable with parameter p. Let M = max(x1,....,xN) (a) Find P{M<} by conditioning on N (b) Find P(M1} (d) Use (b) and (c) to rederive the probability you found in (a).
Answers
suppose they are independent of a geometric random variable with parameter p. Let M = max(x1,....,xN) (a) Find P{M<} by conditioning on N is nλe^(-nλx)
Given fx (x) = λe^λx
Fx (x) = 1 – e^-λx x…0
To find distribution of Min (X1,….Xn)
By applying the equation
fx1 (x) = [n! / (n – j)! (j – 1)!][F(x)]^j-1[1-F(x)]^n-j f(x)
For minimum j = 1
[Min (X1,…Xn)] = [n!/(n-1)!0!][F(x)]^0[1-(1-e^-λx)]^n-1λe^-λx
= ne^[(n-1) λx] λe^(λx)
= nλe^(-λx[1+n-1])
= nλe^(-nλx)
learn more about of variable here
https://brainly.com/question/6472483
#SPJ4
Points A (4, 3), B (6, 4), C (5, 6) and D (3, 5) are the vertices of a square ABCD. The square ABCD is reflected about the line through (0, 0) and (-2, 2). Find the vertices of the image of the square ABCD and present both the figures on the same graph.
Answers
The vertices of the reflected square.
Let's calculate them:
A' = (-0.914, 3.914)
B' = (-2.828, 5.828)
C' = (-0.086, 7.086)
D' = (1.828, 5.172)
The vertices of the image of the square ABCD after reflecting it about the line through (0, 0) and (-2, 2), we can use the following steps:
Find the equation of the reflection line:
The reflection line passes through (0, 0) and (-2, 2).
We can calculate the slope (m) of the line using the formula (y2 - y1) / (x2 - x1):
m = (2 - 0) / (-2 - 0) = 2 / -2 = -1.
Using the point-slope form of a line (y - y1) = m(x - x1), we can use either of the given points to write the equation of the line:
y - 0 = -1(x - 0)
y = -x.
Find the midpoint of each side of the square:
The midpoints of the sides of a square are also the midpoints of its diagonals.
The midpoint of AB is ((4+6)/2, (3+4)/2) = (5, 3.5).
The midpoint of BC is ((6+5)/2, (4+6)/2) = (5.5, 5).
The midpoint of CD is ((5+3)/2, (6+5)/2) = (4, 5.5).
The midpoint of DA is ((3+4)/2, (5+3)/2) = (3.5, 4).
Reflect the midpoints about the line:
To reflect a point (x, y) about the line y = -x, we can find the perpendicular distance (d) from the point to the line and use it to determine the reflected point.
The perpendicular distance d from the line y = -x to a point (x, y) is given by the formula:
d = (y + x) / √(2).
The coordinates of the reflected points can be found using the formula for reflection across a line:
x' = x - 2d / √(2)
y' = y - 2d / √(2).
Calculate the reflected vertices:
The coordinates of the reflected vertices are as follows:
A' = (4 - 2(3.5 + 5) / √(2), 3 - 2(3.5 - 5) / √(2))
B' = (6 - 2(5 + 5) / √(2), 4 - 2(5 - 5) / √(2))
C' = (5 - 2(5.5 + 5) / √(2), 6 - 2(5.5 - 5) / √(2))
D' = (3 - 2(4 + 5) / √(2), 5 - 2(4 - 5) / √(2))
Now we can plot the original square ABCD and its image A'B'C'D' on the same graph to visualize the reflection.
For similar questions on vertices
https://brainly.com/question/1217219
#SPJ8
if you take away 25 from a number you will be left with two and halftimes 30. what is the number?
Answers
If you take away 25 from (100) you get 75.
70 also equals 2.5*30
PLEASE HELP ASAP!!!! I WILL MARK BRAINLIEST!!!!
After getting 5 new rocks, George gave half of his rock collection to Susan. If George gave 36 of his rocks to Susan, which equation could be used to determine how many rocks George started with?
A. 1/2 x = 36 + 6
B. 1/2 (x-5) = 36
C. 1/2x+5=36
D. 1/2 (x+5) = 36
Answers
Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the curves x=√y, x=0, and y=4 about the x-axis.
Answers
The volume generated by rotating the region bounded by the curves \($x = \sqrt{y}$\), \($x = 0$\), and \($y = 4$\) about the x-axis using the method of cylindrical shells is \($4\pi$\) cubic units.
What is the formula for the volume of the cylinder?The formula for the volume of a cylinder is V = πr²h, where V is the volume, r is the radius, and h is the height.
According to given information :To find the volume generated by rotating the region bounded by the curves \($x = \sqrt{y}$\), \($x = 0$\), and \($y = 4$\) about the x-axis using the method of cylindrical shells, we need to follow these steps:
Sketch the region and the axis of rotation. The region bounded by the curves \($x = \sqrt{y}$\), \($x = 0$\), and \($y = 4$\) is a quarter-circle with radius 2 centered at the origin. The axis of rotation is the x-axis.
Choose a vertical strip with width $\Delta x$ that runs parallel to the y-axis and intersects the region. The height of this strip is given by the equation $y = 4 - x^2$.
Imagine rotating this strip around the x-axis to form a cylindrical shell with thickness \($\Delta x$\), height \($4 - x^2$\), and radius \($x$\).
The volume of this cylindrical shell is given by the formula \($V = 2\pi x(4-x^2)\Delta x$\).
To find the total volume of the solid, we need to add up the volumes of all the cylindrical shells. This can be done by taking the limit as the width of the strips $\Delta x$ approaches zero and summing up the volumes of the resulting shells. This gives us the integral:
\($V = \int_{0}^{2} 2\pi x(4-x^2) dx$\)
We can simplify this integral by expanding the expression inside the parentheses, which gives us:
\($V = \int_{0}^{2} 8\pi x - 2\pi x^3 dx$\)
We can then integrate each term separately to get:
\($V = [4\pi x^2 - \frac{1}{2}\pi x^4]_{0}^{2}$\)
\($V = (4\pi \cdot 2^2 - \frac{1}{2}\pi \cdot 2^4) - (4\pi \cdot 0^2 - \frac{1}{2}\pi \cdot 0^4)$\)
\($V = 8\pi - 4\pi = 4\pi$\)
Therefore, the volume generated by rotating the region bounded by the curves \($x = \sqrt{y}$\), \($x = 0$\), and \($y = 4$\) about the x-axis using the method of cylindrical shells is \($4\pi$\) cubic units.
To learn more about the volume of the cylinder visit:
brainly.com/question/6204273
#SPJ1
PLEASE HELP
Suppose that the functions fand g are defined for all real numbers x as follows.
f(x) = 5x
g(x)=4x-4
Write the expressions for (g.f)(x) and (g-f)(x) and evaluate (g+f)(2).
(g•f)(x) =
(g-f)(x) =
(g+r) (2)=
Answers
= 20x^2 - 16
(g - f)(x) = (4x - 4) - (5x)
= (-1x) - 4
= -x -4
(g + f)(2) = (4(2) - 4) + (5(2))
= 4 + 10
= 14
An inner city revitalization zone is a rectangle that is twice as long as it is wide. The width of the region is growing at a rate of 34 m per year at a time when the region is 450 m wide. How fast is the area changing at that point in time?
Answers
Answer:
The area is changing at the point of \(\mathbf{61200 m^2/year}\)
Step-by-step explanation:
From the given information:
Let's recall from our previous knowledge that the formula for finding the area of a rectangle = L × w
where;
L = length and w = width of the rectangle
Suppose the Length L is twice the width w
Then L = 2w --- (1)
From The area of a rectangle
A = L × w
A = 2w × w
A = 2w²
Taking the above differentiating with respect to time
\(\dfrac{dA}{dt }= 4w \times \dfrac{dw}{dt} --- (2)\)
At the time t
\(\dfrac{dw}{dt}= 34 m \ per \ year ; w = 450 \ m\)
Replacing the values back into equation 2, we get:
\(\dfrac{dA}{dt }= 4 \times 450 \times 34\)
\(\mathbf{\dfrac{dA}{dt }= 61200 m^2/year}\)
ميل المستقيم المار بالنقطتين (1,5-), (1,3)
Answers
Answer:
-1
Step-by-step explanation:
(x₁ , y₁) = (1 , 3)
(x₂ , y₂) = (-1 , 5)
\(Slope = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}\\\)
\(=\frac{5 - 3}{-1-1}\\\\=\frac{2}{-2}\\\\= -1\)
Given the following diagram what can you conclude?

Answers
Answer:
YXZ=AXZ
because if you see the letters they form triangle
If you rolled a die, what is the probability that you would roll a 1 or a 2?
Answers
Answer:
1/6 for 1 and 1/6 for 2.
Step-by-step explanation:
Since there are six possible outcomes, the probability of obtaining any side of the die is 1/6. The probability of rolling a 1 is 1/6, the probability of rolling a 2 is 1/6, and so on. If you want the actual fraction, then count up how much 1/6 you rolled. For example, if you rolled a 5 the probability would be 5/6.
Good luck! And I hope you have an awesome day!
For the question of total area of the cuboid is 200cm^.
I understand where we divide 150 by 4.
But why do I need to multiply by 5, when there are 6 faces.
Answers
You need to multiply by 5 instead of 6 because each pair of opposite faces on a cuboid has the same area, so by considering one face from each pair, you ensure that you don't count any face twice.
When calculating the total surface area of a cuboid, you need to understand the concept of face pairs.
A cuboid has six faces, but each face has a pair that is identical in size and shape.
Let's break down the reasoning behind multiplying by 5 instead of 6 in the given scenario.
To find the surface area of a cuboid, you can add up the areas of all its faces.
However, each pair of opposite faces has the same area, so you avoid double-counting by only considering one face from each pair. In this case, you have five pairs of faces:
(1) top and bottom, (2) front and back, (3) left and right, (4) left and back, and (5) right and front.
By multiplying the average area of a pair of faces by 5, you account for all the distinct face pairs.
Essentially, you are considering one face from each pair and then summing their areas.
Since all the pairs have the same area, multiplying the average area by 5 gives you the total surface area.
When dividing 150 by 4 (to find the average area of a pair of faces), you are essentially finding the area of a single face.
Then, by multiplying this average area by 5, you ensure that you account for all five pairs of faces, providing the total surface area of the cuboid.
Thus, multiplying by 5 is necessary to correctly calculate the total surface area of the cuboid by accounting for the face pairs while avoiding double-counting.
For similar question on cuboid.
https://brainly.com/question/29568631
#SPJ8