An amusement park ride is made up of a large circular frame that holds 50 riders. The
circumference of the frame is about 138 ft. What is the diameter of the ride? Round to the nearest
tenth.

Help Please​

Answer:

There are missing and incorrectly placed commas.

There are missing quotation marks.

Step-by-step explanation:

Answer:

A. There are missing quotation marks.

C. There are missing and incorrectly placed commas.

Step-by-step explanation:

edge2021

Answer:

150

Step-by-step explanation:

Answer:

Step-by-step explanation:

Given the expression cos(3x-π) = -√3/2, we are to find the values of x that represent the solutions to the equation.

cos(3x-π) = -√3/2

take inverse cos of both sides

cos⁻¹[cos(3x-π)] = cos⁻¹[-√3/2]

3x-π = cos⁻¹[-√3/2]

3x-π = -30°

since 180° = π rad

Hence;

3x- 180° = -30°

3x =  -30°+ 180°

3x = 150°

x = 150°/3

x = 50°

Since cos is negative in the first second and 3rd quadrant;

3x-180° = -30°

In the second quadrant;

3x-180° = 180-30

3x - 180 = 150

3x = 150+180

3x = 330

x = 110°

In the third quadrant;

3x-180° = 270+30

3x - 180 = 300

3x = 300+180

3x = 480

x = 480/3

x = 160

Answer:

input: $200,5% Output: 10

Step-by-step explanation:

Answer:

n = 3

Step-by-step explanation:

Given

4n = 2n + 6 ( subtract 2n from both sides )

2n = 6 ( divide both sides by 2 )

n = 3

The solution is, n = 3.

Subtraction is the process of taking away a number from another. It is a primary arithmetic operation that is denoted by a subtraction symbol (-) and is the method of calculating the difference between two numbers.

here, we have,

Given

4n = 2n + 6 ( subtract 2n from both sides )

2n = 6 ( divide both sides by 2 )

n = 3

To learn more on subtraction click:

brainly.com/question/2346316

#SPJ5

Answer:

$600...

↓↓↓↓↓

Step-by-step explanation:

25x 24 = 600

(a) To solve for R(x) < 0, we need to find the values of x that make the rational function negative. We can do this by analyzing the sign of each factor in the numerator and denominator.

First, set each factor equal to zero and solve for x:

2x^2 + 3x - 5 = 0 (equation 1)

2x - 5 = 0 (equation 2)

x - 3 = 0 (equation 3)

x + 2 = 0 (equation 4)

Next, determine the sign of each factor for different intervals on the number line. By considering the significant changes between the intervals, we can identify the regions where R(x) is negative.

(b) To find the asymptotes, we examine the denominator of the rational function. In this case, the denominator is (2x - 5)(x + 2). To find the vertical asymptotes, we set the denominator equal to zero and solve for x. In this case, x = 2/5 and x = -2 are the vertical asymptotes.

There are no horizontal or slant asymptotes in this rational function since the degree of the numerator (2) is less than the degree of the denominator (3).

Learn more about rational function here:- brainly.com/question/29098201

#SPJ11

The series ∑5^n/n! converges absolutely by the ratio test

The ratio test is a convergence test that can be used to determine the convergence or divergence of a series of the form ∑a_n, where a_n is a sequence of non-zero real numbers. The test is based on the following idea: if the limit of the ratio of consecutive terms, lim(n → ∞) |a_(n+1)/a_n|, is less than 1, then the series converges absolutely; if the limit is greater than 1, then the series diverges; and if the limit is equal to 1 or does not exist, then the test is inconclusive.

To apply the ratio test to the series ∑5^n/n!, we first need to compute the limit of the ratio of consecutive terms:

r = lim(n → ∞) |5^(n+1)/(n+1)!| * |n!/5^n|

To simplify this expression, we can use the fact that n! = n(n-1)(n-2)...21 and 5^n = 55*...*5 (n times) have a common factor of 5, so we can cancel them out:

r = lim(n → ∞) |5/(n+1)|

Now, as n approaches infinity, the denominator of the fraction n+1 grows without bound, while the numerator remains fixed at 5. Therefore, the limit of the ratio is 0:

r = lim(n → ∞) |5/(n+1)| = 0

Since r is less than 1, we can conclude that the series ∑5^n/n! converges absolutely by the ratio test.

Learn more about convergence

brainly.com/question/31756849

#SPJ11

Answer:

The median is 33.5

Step-by-step explanation:

In order to solve for a median it would either be the middle or it would be the average of the middle if there are even amount of numbers. First you would put them in order. 12 17 28 31 36 54 55 and 71. This would mean the the middle number would be 31 and 36. Since you can't have two medians you would find the average of the two so add 31 and 36 which would be equal to 67 then divide by 2 which would equal to 33.5.

The median of numbers 17, 12, 54, 36, 71, 28, 31, 55 is 33.5.

The median of a set of numbers is the middle value when the numbers are arranged in ascending or descending order.

To find the median of the given numbers, we first need to arrange them in ascending order:

12 17 28 31 36 54 55 71

Since there are an even number of numbers (8), the median will be the average of the two middle values, which are 31 and 36.

To find the average, we add the two numbers and divide by 2:

(31 + 36) / 2 = 67 / 2 = 33.5

Therefore, the median of the given numbers is 33.5.

Learn more about median of numbers in https://brainly.com/question/26177250

#SPJ11

The value of the given triple integral is 486π/5.

What is volume?

A volume is simply defined as the amount of space occupied by any three-dimensional solid. These solids can be a cube, a cuboid, a cone, a cylinder, or a sphere. Different shapes have different volumes.

To evaluate the triple integral ∫∫∫B(x²+y²+z²)² dv using spherical coordinates,

we need to express the integrand and the volume element in terms of spherical coordinates and determine the limits of integration.

In spherical coordinates, the integrand is given by:

f(ρ, θ, φ) = (ρ²)² = ρ⁴

The volume element in spherical coordinates is:

dV = ρ² sin(φ) dρ dθ dφ

The limits of integration for the triple integral are:

0 ≤ ρ ≤ 3 (since B is the ball with center the origin and radius 3)

0 ≤ θ ≤ 2π (since θ ranges over the full circle)

0 ≤ φ ≤ π (since φ ranges over the upper hemisphere)

Therefore, we have:

∫∫∫B(x²+y²+z²)² dv

= ∫₀³ ∫₀²π ∫₀ᴨρ⁴ sin(φ) dφ dθ dρ (substituting in the expression for f(ρ, θ, φ) and dV)

= ∫₀³ ∫₀²π [-ρ⁴ cos(φ)] from φ=0 to φ=π dθ dρ (evaluating the integral with respect to φ)

= ∫₀³ ∫₀²π 2ρ⁴ dθ dρ (since cos(0) - cos(π) = 2)

= ∫₀³ 2πρ⁴ dρ (integrating with respect to θ)

= (2π/5) [ρ⁵] from ρ=0 to ρ=3 (integrating with respect to ρ)

= (2π/5) [3⁵ - 0⁵]

= (2π/5) (243)

= 486π/5

Therefore, the value of the given triple integral is 486π/5.

To know more about volume visit:

https://brainly.com/question/463363

#SPJ4

The median is 25.5, and it represents the typical age of the runners.

The median of a set of numbers is the middle value when the numbers are arranged in ascending or descending order.

In this case, the ages of the 12 runners are:

14, 15, 16, 19, 22, 24, 27, 27, 30, 31, 31, 32

To find the median, which is average of the sixth and seventh values

= 24 +27/2

=  25.5  is the median.

Therefore, the median is 25.5, and it represents the typical age of the runners.

Learn more about median here:

brainly.com/question/28060453

#SPJ1

Answer:

25.5

Step-by-step explanation:

Hence, the plant will be adequate for 10 more years (to the nearest year).

Given, Rate of input to the plant = 200 gallons per day per person

Population of the city = 400,000

Let the population of the city 10 years ago be x gallons per day per person

Then, population of the city 5 years ago = x+ (400000-5000)

= x+ 395000

Thus, rate of input to the plant 10 years ago = 200x gallons per day

After 10 years, population will increase by 5000 and become 405000 people.

Therefore, rate of input to the plant after 10 years = 405000 × 200

= 81,000,000 gallons per day

Now, the plant with capacity of 100 MGD = 100×1000×365×24 gallons per year

= 876,000,000 gallons per year

Thus, the present plant would be adequate for = 876,000,000 ÷ 81,000,000

= 10.81 years

To know more about gallons visit:

https://brainly.com/question/31702678

#SPJ11

Answer:

enter the step by step answer u did and then add the number the match and enter them in the box and u shall be done

Step-by-step explanation:

Answer:

  3 and 1/2 half-cups

Step-by-step explanation:

We are asked to find the number of half-cups that will equal 1 3/4 cups.

__

Let the desired number be represented by n. Then we require ...

  n × 1/2 = 1 3/4 . . . . some number of 1/2-cups will give 1 3/4 cups

Using a common denominator, we have ...

  n × 2/4 = 7/4

Multiplying by the inverse of the coefficient of n gives ...

  n × 2/4 × 4/2 = 7/4 × 4/2

  n = 7/2 = 3 1/2 . . . . . simplify

That is, Donna can measure 1 3/4 cups of sugar by using her 1/2-cup measure 3 times, and filling it half-full for the final 1/4 cup she needs.

She needs 3 1/2 half-cups to get the correct amount.

Using the formula of surface area to calculate the height and using the formula for volume , The answer is 24.98 \(cm^{3}\) .

A cone is a three-dimensional geometric structure with a smooth transition from a flat base—often but not always circular—to the point at the top, also known as the apex or vertex.

The required formula are :

\(SA = \pi r (r + \sqrt {h^{2} + r ^ {2}})\)  (Surface Area)

\(V = \pi r^{2} \frac {h}{3}\) (Volume)

radius = 3 cm

Area= 66 \(cm^{2}\)

\(SA = \pi r (r + \sqrt {h^{2} + r ^ {2}})\)

h = 2.65 cm

\(V = \pi r^{2} \frac {h}{3} = \pi * 3^{2} * \frac {2.65}{3}\)

=24.98 \(cm^{3}\)

To learn more about volumes visit:

https://brainly.com/question/13338592

#SPJ4

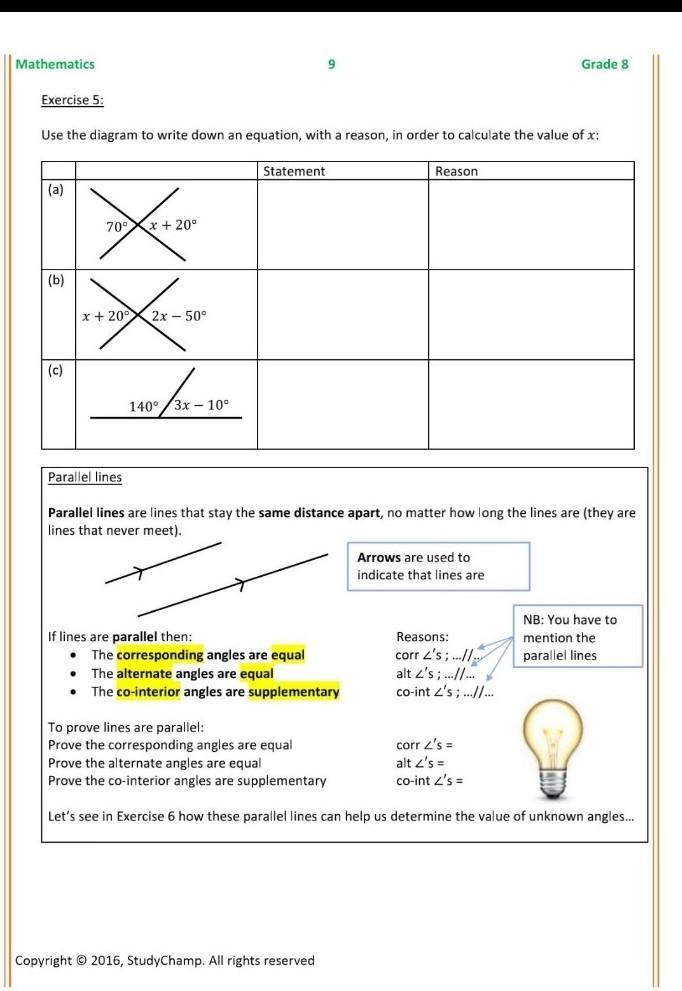
Answer:

Step-by-step explanation:

a) x + 20  = 70                 Vertically opposite angles are congruent

b) 2x - 50 = x + 20           Vertically opposite angles are congruent

c) 3x - 10  + 140 = 180           Linear pair

Answer:

(a) 70= x+20 (vertical angles are equal)

70 - 20=x

50=x

(b) x +20 = 2x -50 (vertical angles are equal)

20 + 50 = 2x - x

70 = x

(c) 140 +3x -10=180 (angles on the straight line)

130 +3x = 180

3x = 180 - 130

3x = 50

x= 50/3

The value of ∫ f(x) dx over the interval [3, 5] is 7. none of the option is correct.

To find the value of ∫ f(x) dx, we need to evaluate the integral of the function f(x) over a given interval. In this case, the function f(x) is defined piecewise:

f(x) = 2 for x < 3

f(x) = x - 1 for x ≥ 3

Let's find the integral of f(x) over a specific interval. We'll consider the interval [3, 5] for this example.

∫ f(x) dx = ∫ [2 for x < 3] + ∫ [x - 1 for x ≥ 3]

Since the lower limit of integration is 3, we'll consider the second part of the piecewise function for the interval [3, 5]:

∫ [x - 1 for x ≥ 3] = ∫ (x - 1) dx from 3 to 5

Now, let's evaluate this integral:

∫ (x - 1) dx = (\(1/2)x^2 - x\) evaluated from 3 to 5

= [\((1/2)(5)^2 - 5] - [(1/2)(3)^2 - 3\)]

= (1/2)(25 - 5) - (1/2)(9 - 3)

= (1/2)(20) - (1/2)(6)

= 10 - 3

= 7

Therefore, the value of ∫ f(x) dx over the interval [3, 5] is 7.

Since the given options for the answer are not specific to any interval, we cannot determine the exact value of the integral without knowing the interval. If there is a specific interval provided, we can evaluate the integral accordingly.

For more suc questions on interval visit:

https://brainly.com/question/30460486

#SPJ8

Answer is 60 % is the percentage of boys studying German .

So, for this one, you must first determine the number of French students.

Simple method:

\(\frac{1}{9}\)  is 270 divided by 9, which equals 30, hence  \(\frac{2}{9}\)of 270 is 60. The result of multiplying \(\frac{1}{9}\) by 2 to get \(\frac{2}{9}\) is 60.

French is being studied by 60.

When you apply this to the French to Spanish ratio of 3:7, you get 3 and 60 on the same side. In order to get to 60, you must multiply 3 by 20. (or divide 60 by 20 to get 3).

Therefore, 20 is the number you use to apply the same formula to the other side of the ratio.

To reach 140, multiply 7 by 20 (or 7 by 10, then multiply that number by 2).

Spanish is being studied by 140.

After subtracting the French and Spanish from the overall number, you are left with 70 German speakers at 270-140-60.

42 of these 70 are males. 28 females are produced by 70-42. The percentage of males studying German is \(\frac{42}{70}\). This is equivalent to \(\frac{6}{10}\), and you multiply a fraction by 10 to convert it to a percentage (\(\frac{60}{100}\) in this case).

Additionally, 60% is equal to \(\frac{60}{100}\)  .

Your response is thus 60%.

For such more questions on Percentage problems:

brainly.com/question/16797504

#SPJ4

The encryption method that combines a random value with the plain text to produce the cipher text is: One-time pad.

The one-time pad encryption technique is a form of symmetric encryption where a random key, known as the one-time pad, is combined with the plain text using a bitwise XOR operation. The one-time pad should be at least as long as the plain text and should never be reused.

In this method, each character of the plain text is combined with a corresponding character from the one-time pad, resulting in the cipher text. The one-time pad acts as a random key stream, making the encryption extremely secure if implemented correctly.

Steganography is a different technique that involves hiding information within other seemingly innocuous data, such as images or audio files, without necessarily encrypting it.

Transposition is a method of encryption where the characters of the plain text are rearranged or shuffled without changing the actual characters themselves.

Elliptic Curve is not an encryption method but rather a mathematical framework used in public-key cryptography systems, such as Elliptic Curve Cryptography (ECC), which provide secure communication channels but do not involve combining random values with the plain text to produce the cipher text.

Therefore, the correct answer is: One-time pad.

To learn more about One time pad

https://brainly.com/question/14859740

#SPJ11

Answer:

(h, k). (2,0)

Answer:

rs 60

1200/20=60......

Answer:

0.2025 or 20.25%

Step-by-step explanation:

The problem says the probability of ONE person having a Dog is 45%

This is 0.45 in decimal form

But what are the chances TWO random people BOTH have Dogs. The chances would decrease!

To find the probability, you need to multiply the probability of one person by the probability of another person. They both have the same probability of having a Dog.

This looks like:

0.45 (person 1)  × 0.45 (person 2) = 0.2025

The number of times 0.45 is in the equation above is the same number as the people in the problem!

Answer:

B

Step-by-step explanation:

susuusjakaajjajajajaajajaj

To find the percentage of all students who like science but not humanities, we need to subtract the percentage of students who chose both science and humanities from the percentage of students who chose science only. 30% of all students like Science but not Humanities.

So, the percentage of students who like science but not humanities is:

41% (students who chose science) - 11% (students who chose both science and humanities) = 30%

Therefore, 30% of all students like science but not humanities.

To find the percentage of students who like Science but not Humanities, we need to subtract the percentage of students who chose both from the percentage who chose Science. Here's the step-by-step explanation:

1. The percentage of students who chose Science: 41%
2. The percentage of students who chose both Science and Humanities: 11%
3. Subtract the percentage of students who chose both from the percentage who chose Science: 41% - 11% = 30%

So, 30% of all students like Science but not Humanities.

Learn more about percentage at: brainly.com/question/29306119

#SPJ11

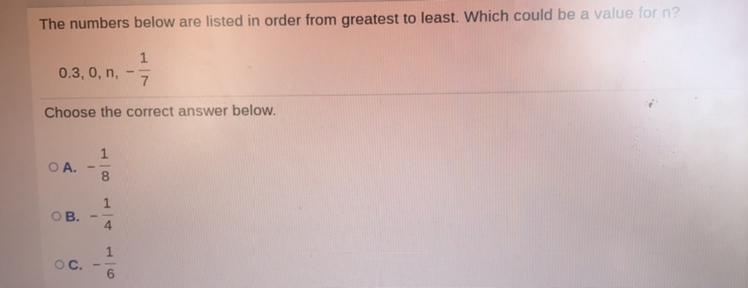
Answer:

-

Step-by-step explanation:

Answer:

-1/8

Step-by-step explanation:

In the negative number line whatever is closest to 0 is greater

-1/8 is -0.125

-1/4 is -0.25

-1/6 is -0.166666667

To find the gradient field of the function f(x,y,z) = ln(2x^2) + 2ln(y^2) + 3ln(z^2), we need to find the partial derivatives of f with respect to x, y, and z. The gradient field of f is given by: F(x,y,z) = (2/x)i + (4/y)j + (6/z)k

∂f/∂x = 4x/2x^2 = 2/x

∂f/∂y = 4y/ y^2 = 4/y

∂f/∂z = 6z/ z^2 = 6/z

So the gradient vector of f is given by:

∇f(x,y,z) = (2/x)i + (4/y)j + (6/z)k

where i, j, and k are the unit vectors in the x, y, and z directions, respectively.

Therefore, the gradient field of f is given by:

F(x,y,z) = (2/x)i + (4/y)j + (6/z)k

Note that the gradient field is a vector field, meaning that at each point in the domain of f, it assigns a vector that points in the direction of the maximum increase of f at that point

Learn more about vector at: brainly.com/question/29740341

#SPJ11

Answer:

The answer is 36

Step-by-step explanation:

=16-4(-5)

=16-(-20)

=36

Answer:

The cubes dimensions are

9 units × 9 units × 9 units

Step-by-step explanation:

Volume (V) = a³

so reverse that and take the cube root of 729

that gives you 9.

hope this helps!

The dimensions of the tank with minimum  weight  is height= 7 and width and length= 14.

The minimum surface area implies that the tank has minimum weight.

Given that the base is square, its width is equal to its length.

Let x= the base width and length of the tank.

Let h = the height .

We are given the volume of the tank that is 1372 ft^3. The formula is given by

V = hx^2

We're given that V = 1,372 ft^3, so

hx^2 = 1,372

h = 1,372 / x^2  ----------(equation 1)

Surface area can be calculated using the below given formula.

A = x^2 + 4xh

Substituting the value of euation 1, h in A, we get,

A = x^2 + 4x(1,372 / x^2)

= x^2 + 5,488 / x

To get the minimum surface area to get the minimum weight, we need to differentiate  A with respect to x and equate it to zero.

dA/dx = 2x - 5,488 / x^2 = 0

2x^3 - 5,488 = 0

x =\(\sqrt[3]{\frac{5,488}{2} }\)

x= 14

We got the value of x, we substitute the value in equation 1, we get the value of h.

h = 1,372 / 14^2

h= 7

So, the dimensions of the tank with minimum weight are width and length is 14 and height is 7.

To learn more on surface area here:

https://brainly.com/question/2835293#

#SPJ4

Continuous on. f(x)=x21x+2 is an illustration of a rational function (the fraction of two polynomials).

A rational function is any function that can be formally stated as an algebraic fraction in which both the numerator and the denominator are polynomials. The coefficients of the polynomials may appear in any field K and need not be rational values. A function that measures two polynomials in comparison. As a ratio, it is "rational" because one is divided by the other. Write the number in decimal form before determining whether it is rational or irrational if you are required to do so. The number is rational if it comes to an end. You should search for a recurring pattern of digits if it goes on forever. The number is irrational if there is no pattern that repeats itself.

Determine the continuous of the function.

Continuous on.

Learn more about rational function here

https://brainly.com/question/1851758

#SPJ4

The function f(x) = (x^2 - 1)/(x + 2) is a rational function that is continuous for all values of x except x = -2. This is because division by zero is undefined, and the denominator of the function becomes zero at x = -2.

The given function f(x) = (x^2 - 1)/(x + 2) is a rational function, which is a fraction of two polynomials. To check the continuity of the function, we need to find any values of x that make the denominator equal to zero since division by zero is undefined. In this case, the denominator becomes zero at x = -2, so the function is discontinuous at x = -2. Therefore, f(x) is continuous for all values of x except x = -2. This means that the function is defined and has a well-defined output value for every input value, except when x is equal to -2.

Learn more about polynomials here: brainly.com/question/11536910

#SPJ4