Alexander found the means to MAD ratio of 2 data sets to be 2. 1
What can he conclude Bout the distributions?
Answers
Alexander can conclude that the inconstancy (spread) of the information in one dataset is twice as much as the changeability of the information within the other dataset.
The mean absolute deviation (MAD) could be a degree of inconstancy that depicts the normal separation between each information point and the cruelty of the dataset. The bigger the Frantic esteem, the more spread out the information is. The proportion of the implies to MADs of two datasets can be utilized to compare their spread.
In this case, the proportion of implies to MADs is 2.1. This implies that the cruelty of one dataset is 2.1 times bigger than the Frantic of that dataset, whereas the cruelty of the other dataset is as if it were 1 times bigger than its Frantic. Hence, the dataset with the bigger proportion (2.1) encompasses a bigger spread (inconstancy) compared to the other dataset.
To learn about mean absolute deviation visit:
https://brainly.com/question/10528201
#SPJ4
Related Questions
15 + ax/5=10 solve for x
Answers
Answer:
25/4
Step-by-step explanation:
I just did it and got It right on M period
The value of x = -25/ a
What is the solution for an equation?The solution of an equation refers usually to the values of the variables involved in that equation which if substituted in place of those variable would give a true mathematical statement.
WE have been given an equation 15 + ax/5=10. we need to solve for x
15 + ax/5=10
Subtract 10 from, both side then
15 - 10+ ax/5=10 -10
15 - 10+ ax/5= 0
5 + ax/5= 0
Now subtract ax/5 on both side we get
5 = -ax/5
Cross multiplication;
25 = -ax
Therefore, the value of x = -25/ a
Learn more about solving equations here:
https://brainly.com/question/13072448
#SPJ2
Please help me. I will mark brainliest

Answers
Answer:
Step-by-step explanation:
Please help me thank youu

Answers
Answer:
(2,-3)
Step-by-step explanation:
-6/-3 = 2 and 18/-6 = -3
Yesterday the temperature at noon was 15.1°F. By midnight, it had dropped by
24.2°F. What was the temperature at midnight?
Answers
Answer:
-9.1 degrees at midnight
Step-by-step explanation:
15.1 - 24.2 = -9.1 degrees
Describe a situation with an output of area in square feet that can be modeled using the function f(x)

Answers
Step-by-step explanation: The area of a rectangular garden can be represented by the function
f(x) = x(2x + 5)
Find the area if the length, x, is 3 feet.
2. Discounts - You go to the store the next day and the $28.62 shirt is on sale for 15%
off, how much is the shirt before tax?
Answers
Answer:
a = 15 /100 * 28.62 = 4293 /1000
= 4.293
Hope this helps! :)
Find the remaining zeros of f using the given information about the polynomial.
Then write the linear factorization of the polynomial. Degree 4;
zeros: 3i, square root {7}
Answers
Answer:
noloce necesito puntos
one thousand dollars is deposited in a savings account where the interest is compounded continuously. after 6 years, the balance will be $1370.55 . when will the balance be $1711.03 ? round to the nearest tenth of a year.
Answers
If the balance will be $1370.55 after 6 years, then The balance will be $1711.03 after approximately 14.3 years.
The formula for calculating the balance in a continuously compounded account is:
\(A = Pe^{rt}\)
Where:
A = final balance
P = principal (initial deposit)
e = Euler's number (approximately 2.71828)
r = annual interest rate
t = time in years
We know that the initial deposit is $1000 and the balance after 6 years is $1370.55, so we can use these values to solve for the annual interest rate:
\(1370.55 = 1000*e^{6r}\)
⇒ \(ln(\frac{1370.55}{1000}) = 6r\)
⇒ \(r = \frac{ln(\frac{1370.55}{1000})}{6}\)
⇒ \(r = 0.0345\)
Now we can use the same formula to find out when the balance will be $1711.03:
\(1711.03 = 1000*e^{(0.0345*t)}\)
⇒ \(ln(\frac{1711.03}{1000}) = 0.0345*t\)
⇒ \(t = \frac{ln(\frac{1711.03}{1000})}{0.0345}\)
⇒ t = 14.3 years.
To know more about interest
brainly.com/question/28792777
#SPJ4
Simplify the given polynomials. Then, classify each by its degree and number of terms.

Answers
Expression 1:
Degree: 2
Number of terms: 3
It is quadratic.
Expression 2:
Degree: 1
Number of terms: 2
It is a binomial.
Expression 3:
Degree: 0
Number of terms: 1
It is constant.
We have,
Expression 1: (3x - 1/4)(4x + 8)
Expanding the expression using the distributive property:
= 3x x 4x + 3x x 8 - (1/4) x 4x - (1/4) x 8
= 12x² + 24x - (4/4)x - 2
= 12x² + 24x - x - 2
= 12x² + 23x - 2
The degree of this expression is 2 because the highest power of x is 2.
There are 3 terms in this expression.
Expression 2:
(5x² + 7x) - (1/2) (10x² - 4)
Distributing the negative sign inside the parentheses:
= 5x² + 7x - (1/2)(10x²) + (1/2)(4)
= 5x² + 7x - 5x² + 2
= 7x + 2
The degree of this expression is 1 because the highest power of x is 1.
There are 2 terms in this expression.
Expression 3:
3(8x² + 4x - 2) + 6(-4x² - 2x + 3)
Expanding and simplifying each term:
= 3 x 8x² + 3 x 4x + 3 x (-2) + 6 x (-4x²) + 6 x (-2x) + 6 x 3
= 24x² + 12x - 6 - 24x² - 12x + 18
= (24x² - 24x²) + (12x - 12x) + (-6 + 18)
= 0x² + 0x + 12
= 12
The degree of this expression is 0 because there is no x term.
There is 1 term in this expression.
Thus,
Expression 1:
Degree: 2
Number of terms: 3
It is quadratic.
Expression 2:
Degree: 1
Number of terms: 2
It is a binomial.
Expression 3:
Degree: 0
Number of terms: 1
It is constant.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
i really need to know this or imma fail!!!!!!!

Answers
The answer to the simplified expression 4⁹/4³ in index form is derived to be equal to 4⁶
How to simplify fraction of numbers in index formTo simplify a fraction written in index form, you can first express the numbers in prime factorization form by writing both the numerator and denominator as a product of prime factors. Identify common prime factors in the numerator and denominator and cancel them out. Then write the remaining factors as a product in index form.
Given the fraction 4⁹/4³, we can simplify as follows:
4⁹/4³ = (4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4)/(4 × 4 × 4)
we can cancel out (4 × 4 × 4) from both the numerator and denominator, living us with;
4⁹/4³ = 4 × 4 × 4 × 4 × 4 × 4
4⁹/4³ = 4⁶
Therefore, the answer to the simplified expression 4⁹/4³ in index form is derived to be equal to 4⁶
Read more about index here:https://brainly.com/question/15361818
#SPJ1
The table shows the number of miles driven over time.

Answers
solve the literal equation for y.
117. y - 2x = 14
Answers
Answer:
y = 14 + 2x
Step-by-step explanation:
pleas help with this question
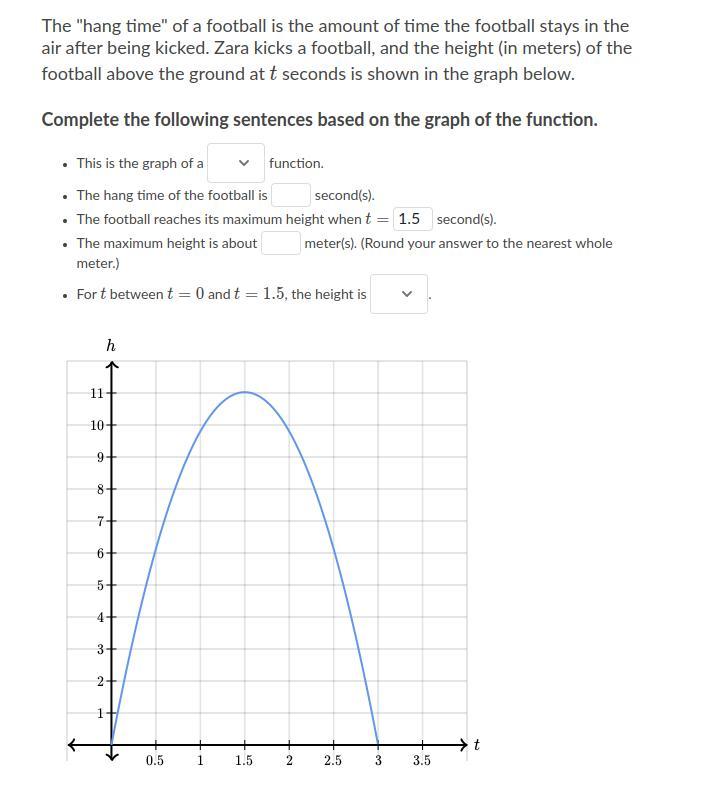
Answers
Answer:
Look in the explanation
Step-by-step explanation:
This is the graph of a parabolic function
The hang time is 3 seconds
The maximum height is about 11 meters
for t between t=0 , t=1.5, the height is increasing
If z=(x+y)e^y and x=3t and y=1- t2, find the following derivative using the chain rule. Enter your answer as a function of t.
dz/dt =
Answers
The derivative dz/dt can be found by applying the chain rule. Let's first substitute the given expressions for x and y into the equation for z:
z = (x + y)e^y
z = (3t + 1 - t^2)e^(1 - t^2)
Now, we can differentiate z with respect to t using the chain rule. The chain rule states that if u = f(g(t)), then du/dt = f'(g(t)) * g'(t).
Applying the chain rule to the given equation, we have:
dz/dt = d((3t + 1 - t^2)e^(1 - t^2))/dt
To differentiate this expression, we need to consider the derivative of each term. Let's break it down:
1. The derivative of 3t with respect to t is simply 3.
2. The derivative of 1 with respect to t is 0 since it is a constant.
3. The derivative of -t^2 with respect to t is -2t.
4. The derivative of e^(1 - t^2) with respect to t can be found using the chain rule again.
For the fourth term, let's define u = 1 - t^2. The derivative of u with respect to t is du/dt = -2t. Now, we have:
dz/dt = (3 + 0 - 2t)e^(1 - t^2) + (3t + 1 - t^2)d(e^(1 - t^2))/dt
Using the chain rule once more, we differentiate e^(1 - t^2) with respect to u:
d(e^(1 - t^2))/du = e^(1 - t^2) * d(1 - t^2)/dt
The derivative of 1 - t^2 with respect to t is -2t. Substituting this back into our expression, we get:
dz/dt = (3 + 0 - 2t)e^(1 - t^2) + (3t + 1 - t^2)(-2t)e^(1 - t^2)
Simplifying the expression, we have:
dz/dt = (3 - 2t)e^(1 - t^2) - 2t(3t + 1 - t^2)e^(1 - t^2)
Therefore, the derivative dz/dt is given by (3 - 2t)e^(1 - t^2) - 2t(3t + 1 - t^2)e^(1 - t^2), where e represents the exponential function.
To learn more about derivatives click here: brainly.com/question/29144258
#SPJ11
What is the area of a hexagon with an apothem of 24 m?
Answers
Answer:
Area of Hexagon = 1,995 m² (Approx.)
Step-by-step explanation:
Given:
Length of apothem = 24 m
Number of total sides = 6
Find:
Area of Hexagon
Computation:
Side = a[2tan(180/n)]
Side = 24[2tan(180/6)]
Side = 24[2tan(30)]
Side = 27.71 m (Approx.)
Area of Hexagon = [3√3a²]/2
Area of Hexagon = [3(1.732)(27.71)²]/2
Area of Hexagon = [3(1.732)(767.8441)]/2
Area of Hexagon = 3989.71794 / 2
Area of Hexagon = 1994.8589
Area of Hexagon = 1,995 m² (Approx.)
What is the distance from (−5, −19) to (−5, 32)? HELPP
13 units
51 units
−13 units
−51 units
Answers
The distance between the given coordinates (−5, −19) and (−5, 32) is given by 51 units.
Let us consider the coordinates of two given points be,
(x₁ , y₁ ) = ( -5 , -19 )
(x₂ , y₂ ) = (-5 , 32 )
Distance formula between two points is equals to,
Distance = √ ( y₂ - y₁)² + ( x₂ - x₁ )²
Substitute the values of the coordinates we have,
⇒ Distance = √ ( 32 - (-19))² + ( -5- (-5) )²
⇒ Distance = √ (32 +19)² + (-5 + 5)²
⇒ Distance = √ 51² + 0²
⇒ Distance = 51 units.
Therefore, the distance between the two points is equal to 51 units.
Learn more about distance here
brainly.com/question/31628069
#SPJ1
Simplify fully
a) 12x5 + 3x2
b) 15y = 3y2
Please

Answers
Answer:
I think the a. is 4x^3 and b. is 5y^5
Zontini the Amazing Hypnotist is hypnotizing a volunteer at a performance by
swinging a pocket watch back and forth in front of her face. The pocket watch's
current distance from center in centimetres in terms of time is modelled by the
equation d(s) = 7 sin(360s). If Zontini the Amazing Hypnotist were to swing the watch
twice as fast, covering the same distance, how would the equation change?
Answers
Answer:
The equation will change by an increase in the angular frequency of motion by a factor of 2 to become d(s) = 7·sin(720s)
Step-by-step explanation:
The given oscillatory motion equation of the swinging pocket watch is d(s) = 7sin(360s)
The general equation of simple harmonic motion is x = A·sin(ω₁t + ∅)
Comparing, we have;
x = d(s)
A = 7
ω₁t = 360
∅ = 0
The period of oscillation = The time to complete a cycle = 2·π/ω₁
Therefore;
ω₁ = 2·π/T₁
When the cycle or the watch swing rate is doubled, the time taken to compete one cycle is halved and the new period, T₂ = T₁/2
ω₂ = 2·π/T₂ = 2·π/(T₁/2) = 4·π/T₁ = 2ω₁
The equation becomes;
x = A·sin(ω₂t) = A·sin(2ω₁t) which gives;
d(s) = 7·sin(2 × 360s) = 7·sin(720s)
The equation will change by the doubling of the angular frequency of the motion
The lyric, "Historians research more than just the word of one/To learn all sides of history" most closely means that
Which?

Answers
Answer:
I would say C
Step-by-step explanation:
I said C because when people look for information they look at different sources instead of just one.
what is f(x) = 2 ∗ 5−x
Answers
x=10 if you are looking for the x value
Step-by-step explanation:
A cell phone plan costs $ 28.90 per month for 400 minutes of talk time. It costs an additional $ 0.05 per minute for each minute over 400 minutes. To get e-mail access, it costs 20% of the price for minutes of talk time. Your bill, which includes e-mail, is the same each month for 7 months. The total cost for all 7 months is $273.91. Write and solve an equation to find the number of minutes of talk time you use each month.
Equation: 273.91 = 7 (0.05m + 28.90 + 0.20(28.90))
Please find the solution.
Answers
The number of minutes of talk time used each month is 89. The solution has been obtained by using linear equation.
What is a linear equation?
The linear equation has a degree of 1. It is evident that there are no variables in linear equations with exponents greater than one. This graph's equation produces a straight line.
We are given that a cell phone plan costs $ 28.90 per month for 400 minutes of talk time and the related information.
Let m be the number of minutes of talk time
From this, we get an equation as
273.91 = 7 (0.05m + 28.90 + 0.20(28.90))
On solving the equation, we get
⇒273.91 = 7 (0.05m + 28.90 + 5.78)
⇒273.91 = 0.35m + 202.3 + 40.46
⇒273.91 = 0.35m + 242.76
⇒0.35m = 31.15
⇒m = 89
Hence, the number of minutes of talk time used each month is 89.
Learn more about linear equation from the given link
brainly.com/question/30092358
#SPJ1
You are the manager of a firm that sells its product in a competitive market at a price of $60. Your firm's cost function is C = 50 + 3Q2. Your firm's maximum profits are: the answer is $250.
Answers
For the given cost function, the maximum profit is $250.
What is profit maximization?
According to the firm theory, a company is founded with the intention of maximizing profits.
A company must run at the lowest possible cost while maximizing revenues in order to accomplish this.
When marginal costs and marginal revenue are identical, profits are maximized.
Profit = Total revenue - total costTotal revenue = Selling price - quantity soldTotal cost = Fixed cost + variable cost1. Determine the profit maximizing output.
For a firm in a competitive market, the marginal revenue is equal to the price (MR = P)
Get the MC by differentiating the total cost with respect to the quantity (Q)
C = 50 + 3Q^2
dC / dQ =6Q
MC = 6Q
Profit will be maximized when: MR = MC
MR = MC
60 = 6Q
Q =10
This is the profit maximizing output.
2. To get the maximum profits substitute this value into the equation:
Profit = Total revenue - Total cost
Profit = (P*Q) - (50 + 3Q^2)
Profit = (60*10) - (50 + 3*10^2)
Profit = 600 - 350
Profit = 250
Hence, for the given cost function, the maximum profit is $250.
To know more about profit maximization, click on the link
https://brainly.com/question/13464288
#SPJ4
Would like to know how to solve step by step in depth.No idea how to solve this help!

Answers
Solution:
y=mx^2-5x-2
To find x-intercepts we must equal y to zero:
y=0→mx^2-5x-2=0
This is a quadratic equation, and we can solve it using the quadratic formula:
ax^2+bx+c=0; a=m, b=-5, c=-2
x=[-b +- sqrt( b^2-4ac) ] / (2a)
x=[-(-5) +- sqrt( (-5)^2-4(m)(-2) ) ] / (2(m))
x=[5 +- sqrt(25+8m)] / (2m)
This equation doesn't have solution (no x-intercepts) if:
25+8m<0
This is an inequality. Solving for m: Subtracting 25 both sides of the inequality:
25+8m-25<0-25
8m<-25
Dividing both sides of the inequality by 8:
(8m) / 8 < (-25) / 8
m<-25/8
Answer: The graph of y=mx^2-5x-2 have no x-intercepts for m<-25/8
Use Inverse Laplace Transformation to convert s-domain to time-domain function for the following functions
a)
F(s) = \(\large{\frac{2e^{-0.5s}}{s^2-6s+9}}\)
\(f(t)=\) ....
b)
F(s) = \(\large{\frac{s-1}{s^2-3s+2}}\)
\(f(t)=\) .....
c)
F(s) = \(\large{\frac{s-1}{s^2+s-2}}\)
\(f(t)=\) ....
d)
F(s) = \(\large{\frac{e^{-s}(s-1)}{s^2+s-2}}\)
\(f(t)=\) ....
Answers
The inverse Laplace transform of F(s) is:
\(f(t) = e^(-t)\)
How did we get the value?To find the inverse Laplace transform of each function, we need to express them in terms of known Laplace transforms. Here are the solutions for each function:
a)
\(F(s) = \large{\frac{2e^{-0.5s}}{s^2-6s+9}}\)
To find the inverse Laplace transform, we first need to factor the denominator of F(s). The denominator factors as (s - 3)². Therefore, we can rewrite F(s) as:
\(F(s) = \large{\frac{2e^{-0.5s}}{(s-3)^2}}\)
Now, we know that the Laplace transform of eᵃᵗ is 1/(s - a). Therefore, the inverse Laplace transform of
\(e^(-0.5s) \: is \: e^(0.5t).\)
Applying this, we get:
\(f(t) = 2e^(0.5t) * t \\
b) F(s) = \large{\frac{s-1}{s^2-3s+2}}\)
We can factor the denominator of F(s) as (s - 1)(s - 2). Now, we rewrite F(s) as:
\(F(s) = \large{\frac{s-1}{(s-1)(s-2)}}\)
Simplifying, we have:
\(F(s) = \large{\frac{1}{s-2}}\)
The Laplace transform of 1 is 1/s. Therefore, the inverse Laplace transform of F(s) is:
\(f(t) = e^(2t) \\
c) F(s) = \large{\frac{s-1}{s^2+s-2}}
\)
We factor the denominator of F(s) as (s - 1)(s + 2). The expression becomes:
\(F(s) = \large{\frac{s-1}{(s-1)(s+2)}}\)
Canceling out the (s - 1) terms, we have:
\(F(s) = \large{\frac{1}{s+2}}\)
The Laplace transform of 1 is 1/s. Therefore, the inverse Laplace transform of F(s) is:
\(f(t) = e^(-2t) \\
d) F(s) = \large{\frac{e^{-s}(s-1)}{s^2+s-2}}\)
We can factor the denominator of F(s) as (s - 1)(s + 2). Now, we rewrite F(s) as:
\(F(s) = \large{\frac{e^{-s}(s-1)}{(s-1)(s+2)}}\)
Canceling out the (s - 1) terms, we have:
\(F(s) = \large{\frac{e^{-s}}{s+2}}\)
The Laplace transform of
\(e^(-s) \: is \: 1/(s + 1).\)
Therefore, the inverse Laplace transform of F(s) is:
\(f(t) = e^(-t)\)
learn more about inverse Laplace transform: https://brainly.com/question/27753787
#SPJ4
Find the Surface area of the trapezoid
please help
show work

Answers
Answer:
259.5
Step-by-step explanation:
8.1*12=97.2
Area of trapiezium = 1/2(b+a)h
(2.8+8.1)=10.9
10.9*3/2=16.35
16.35*2=32.7
2.8*12=33.6
33.6+32.7+97.2=163.5
4*12*2=96
163.5+96=259.5
Determine the coordinates of the vertices of the rectangle to compute the area of the rectangle using the distance formula (round to the nearest integer). A) 39 units2 B) 52 units2 C) 64 units2 D) 78 units2
Answers
Answer:
78
Step-by-step explanation:
I just got it right
Of the 4 students who owned a TI calculator, 2 had graphing calculators. Estimate the proportion of students who do not own a TI graphing calculator. 2 Incorrect: Your answer is incorrect.
Answers
Based on the given information, we can estimate that out of the total population of students, 2 out of 4 students (or 50%) own graphing TI calculators so it can be estimated that the proportion of students who do not own a TI graphing calculator is 50%.
To estimate the proportion of students who do not own a TI graphing calculator, we can use the information provided that out of the 4 students who owned a TI calculator, 2 had graphing calculators. Since we know that all graphing calculators are TI calculators, we can assume that the 2 students with graphing calculators are included in the total count of students who own TI calculators. Therefore, the remaining 2 students who own TI calculators must have non-graphing calculators.
Based on this information, we can estimate that out of the total population of students, 2 out of 4 students (or 50%) own non-graphing TI calculators. Therefore, we can estimate that the proportion of students who do not own a TI graphing calculator is 50%.
It's important to note that this is an estimation based on the limited information provided. To obtain a more accurate estimate, a larger sample size or more comprehensive data would be needed. Additionally, this estimation assumes that the sample of 4 students is representative of the entire student population in terms of calculator ownership. If there are any biases or limitations in the sampling method or if the sample is not representative, the estimate may not accurately reflect the true proportion of students who do not own a TI graphing calculator.
Learn more about estimate here:
brainly.com/question/30876115
#SPJ11
Please check my work!

Answers
Hi, so for A. You need to rewrite 19 as -19
And for B. You need to rewrite 15 as -15
Otherwise everything seems correct
Find the area of the figure. (Sides meet at right angles.)
13 m
5 m
3 m
5 m
2 m
2 m
5 m
5 m

Answers
2) 3x3=9
3)5x5=25
All= 25+9+25 = 59m
The area of the figure is 59 m².
What is a square?Square is a two-dimensional figure that has four sides and all four sides are equal.
The area of a square is side²
We have,
The figure has three squares.
Two similar squares and one square.
Similar square:
Side = 5 m
Another square:
Side = 3 m
Now,
Area of the figure.
= Area of the similar square + Area of the another square
= 2 x side² + side²
= 2 x 5² + 3²
= 2 x 25 + 9
= 50 + 9
= 59 m²
Thus,
The area of the figure is 59 m².
Learn more about squares here:
https://brainly.com/question/22964077
#SPJ2
1. An investor deposits $1000 in an account that promises an annual interest rate of 5%,
compounded at the end of each year. How much will be in the account after seven years?
Answers
Answer:
$1,407.10
Step-by-step explanation:
1000(1.05)^7 = 1.05^7 ≈ 1.40710 * 1000 = $1,407.10