According to Boyle's Law, if the temperature of a confined gas is held fixed, then the product of the pressure P and the volume V is a constant, suppose that, for a certain gas, PV=800 where P is measured in pounds per square inch and V is measured in cubic inches. Answer the following: (this is calculus)
A) Find the average rate of change of P as V increases from 200in^3 to 250in^3.
B) Express V as a function of P and show that the instantaneous rate of change of V with respect to P is inversely proportional to the square of P.
Answers
If PV = 800, then P can be written as a function of V,
P(V) = 800 / V
(a) The average rate of change of P as V increases from 200 to 250 in³ is then
(P (250) - P (200)) / (250 in³ - 200 in³) = (3.2 lb/in² - 4lb/in²) / (50 in³)
... = -0.016 (lb/in²)/in³
(Or -0.016 lb/in⁵, but I figure writing the rate as (units of pressure) per (unit volume) makes more sense.)
(b) We can also write V as a function of P :
V(P) = 800 / P
Take the derivative:
V'(P) = - 800 / P²
which immediately demonstrates that V'(P) ∝ 1 / P², as required. (The fish-looking symbol, ∝, means "is proportional to".)
If differentiating is supposed to be more involved, you can use the limit definition:
\(V'(P)=\displaystyle\lim_{h\to0}\frac{V(P+h)-V(P)}h\)
\(V'(P)=\displaystyle\lim_{h\to0}\frac{\frac{800}{P+h}-\frac{800}P}h\)
\(V'(P)=\displaystyle\lim_{h\to0}\frac{\frac{800P-800(P+h)}{P(P+h)}}h\)
\(V'(P)=\displaystyle800\lim_{h\to0}\frac{-\frac h{P(P+h)}}h\)
\(V'(P)=\displaystyle-800\lim_{h\to0}\frac1{P(P+h)}=-\dfrac{800}{P^2}\)
Part(a): The average rate of change of \(\frac{dP}{dV}\) is \(-0.0164 lb/in^{2}\)
Part(b): The required answer is \(\frac{dV}{dP} \infty \frac{1}{P^{2}}\)
Part(a):
Given,
\(PV=800\)
Differentiating the above equation with respect to \(V\).
\(\frac{dP}{dV}=-\frac{P}{V}\)
Now, at \(V=200 in^{3}\) and \(P=4 lb/in^2\)
At \(V=250 in^3\) and \(P=\frac{80}{25} lb/in^2\)
Hence, we can write,
\(\frac{dP}{dV}\) at \(V=200\) we get,
\(\frac{-1}{200}=\frac{-1}{50}\)
Again \(\frac{dP}{dV}\) at \(V=250\) we get,
\(\frac{-80}{25\times 250}\)
So, the average rate of change of \(\frac{dP}{dV}\) is,
\(\frac{-\frac{1}{50}- \frac{8}{25\times25} }2\\=-\frac{1}{100}-\frac{1}{625}\\=-0.0164 lb/in^2\)
Part(b):
Given,\(PV=800\) then,
\(V=\frac{800}{P}\)
Now,\(\frac{dV}{dP} =-\frac{800}{P^2}\)
Then the above implies,
\(\frac{dV}{dP} \infty \frac{1}{P^{2}}\)
Learn more:https://brainly.com/question/12817429
Related Questions
Write down all the prime numbers between 41
Answers
Answer: Step-by-step explanation:
List of prime numbers before 41 (including 41 itself): 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41.
Hello I need help with question 11 ! I will give you a great rating! Please help, I’m not sure how to do this. Also this is not a quiz this is practice
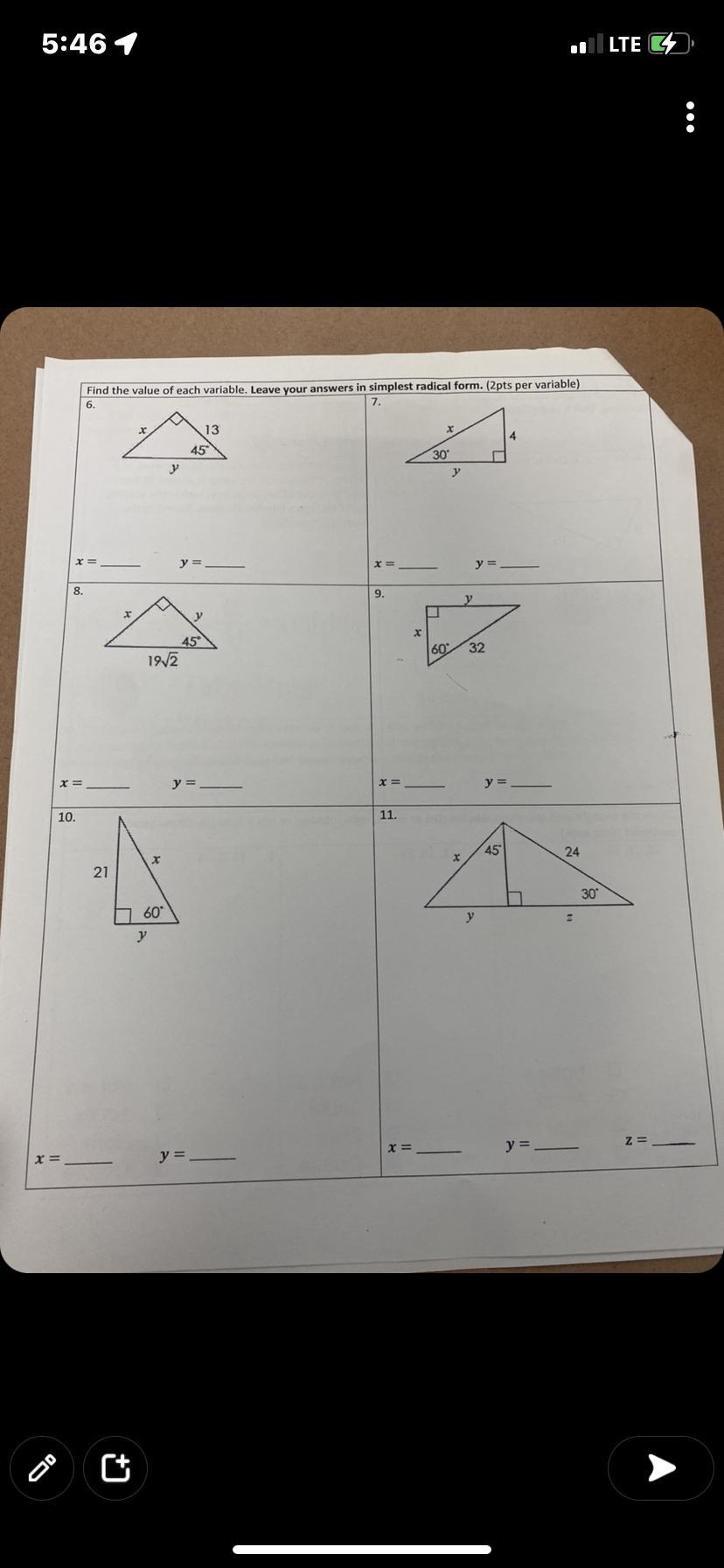
Answers
Solution:
Given the ΔABC as shown below:
To evaluate the value of x, y, and z,
Let's begin with z.
Step 1: In the ΔBCD, identify the sides.
Thus, in the triangle BCD,
\(\begin{gathered} BC\Rightarrow hypotenuse \\ BD\Rightarrow opposite \\ DC\Rightarrow adjacent \end{gathered}\)Step 2: Evaluate the value of z, using trigonometric ratios.
From trigonometric ratios,
\(\begin{gathered} sin\text{ }\theta=\frac{opposite}{hypotenuse} \\ cos\text{ }\theta=\frac{adjacent}{hypotenuse} \\ tan\text{ }\theta=\frac{opposite}{adjacent} \end{gathered}\)Thus, we have
\(\begin{gathered} cos\text{ }\theta=\frac{adjacent}{hypotenuse} \\ where \\ \theta\Rightarrow\angle C=30 \\ adjacent\Rightarrow DC=z \\ hypotenuse\Rightarrow BC=24 \\ thus, \\ cos\text{ 30=}\frac{z}{24} \\ cross-multiply, \\ z=24\times cos\text{ 30} \\ =24\times\frac{\sqrt{3}}{2} \\ \Rightarrow z=12\sqrt{3} \end{gathered}\)To evaluate the values of x and y, we need to first evaluate the value of BD.
Thus,
\(\begin{gathered} \sin\theta=\frac{opposite}{hypotenuse} \\ where \\ \theta=30 \\ opposite=BD \\ hypotenuse=BC=24 \\ thus, \\ \sin30=\frac{BD}{24} \\ cross-multiply, \\ BD=24\times sin\text{ 30} \\ =24\times\frac{1}{2} \\ \Rightarrow BD=12 \end{gathered}\)Thus, to evaluate the value of x,
step 1: In the ΔABD, identify the sides of the triangle.
Thus, in the triangle ABD,
\(\begin{gathered} hypotenuse\Rightarrow AB \\ opposite\Rightarrow AD \\ adjacent\Rightarrow BD \end{gathered}\)Step 2: Evaluate the value of x, using trigonometric ratios.
From trigonometric ratios,
\(\begin{gathered} cos\text{ }\theta=\frac{adjacent}{hyptenuse} \\ where \\ \theta\Rightarrow\angle B=45 \\ adjacent\Rightarrow BD=12 \\ hypotenuse\Rightarrow AB=x \\ thus, \\ cos\text{ 45 = }\frac{12}{x} \\ cross-multiply, \\ x\times cos\text{ 45 = 12} \\ \Rightarrow x\times\frac{\sqrt{2}}{2}=12 \\ divide\text{ both sides by }\frac{\sqrt{2}}{2}, \\ x=12\times\frac{2}{\sqrt{2}}=\frac{24}{\sqrt{2}} \\ rationalize\text{ the denominator of the surd,} \\ x=\frac{24\sqrt{2}}{\sqrt{2}}\times\frac{\sqrt{2}}{\sqrt{2}}=\frac{24\sqrt{2}}{2} \\ \Rightarrow x=12\sqrt{2} \end{gathered}\)To evaluate the value of y,
In the triangle ABD, using trigonometric ratios,
\(\begin{gathered} \tan\theta=\frac{opposite}{adjacent} \\ where \\ \theta=45 \\ opposite\Rightarrow AD=y \\ adjacent\Rightarrow BD=12 \\ thus, \\ \tan45=\frac{y}{12} \\ cross-multiply, \\ y=12\times\tan45 \\ =12\times1 \\ \Rightarrow y=12 \end{gathered}\)Hence, the values of x, y and z are
\(\begin{gathered} x=12\sqrt{2} \\ y=12 \\ z=12\sqrt{3} \end{gathered}\)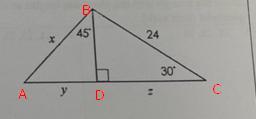
ap calculus problem
no need full detail solution

Answers
The Taylor series for f(x) = e^2x at x = 1 is option D. Σ2ⁿ e²ˣ/n! (x - 1)ⁿ
How did we get the value?The Taylor series for a function f(x) centered at x = a is given by:
f(x) = f(a) + f'(a)(x-a)/1! + f''(a)(x-a)^2/2! + f'''(a)(x-a)^3/3! + ...
f'(a), f''(a), f'''(a), ... depict the first, second, third, and higher derivatives of f(x) evaluated at x = a.
In this case:
f(x) = e^(2x)
The first derivative is:
f'(x) = 2e^(2x)
The second derivative is:
f''(x) = 4e^(2x)
The third derivative is:
f'''(x) = 8e^(2x) etc.
Finding the Taylor series for f(x) = e^(2x) at x = 1, evaluate each derivative at x = 1:
f(1) = e^(2)
f'(1) = 2e^(2)
f''(1) = 4e^(2)
f'''(1) = 8e^(2) etc.
Plug these values into the Taylor series formula:
f(x) = f(1) + f'(1)(x-1)/1! + f''(1)(x-1)^2/2! + f'''(1)(x-1)^3/3! + ...
f(x) = e^(2) + 2e^(2)(x-1)/1! + 4e^(2)(x-1)^2/2! + 8e^(2)(x-1)^3/3! + ...
Simplify:
f(x) = e^(2) + 2e^(2)(x-1) + 2e^(2)(x-1)^2 + 4e^(2)(x-1)^3/3 + ...
Therefore, the Taylor series for f(x) = e^(2x) at x = 1 is: Σ2ⁿ e²ˣ/n! (x - 1)ⁿ which is option D.
learn more about Taylor series: https://brainly.com/question/28168045
#SPJ1
The graph below represents which of the following functions?

Answers
Answer:
D
Step-by-step explanation:
The correct answer is D, try graphing them on desmos.
Which ordered pair is a solution of the equation shown? A.-3/4,- 1/2 B. 0,3/4 C.4/3, 1/2 D. 4, 3/2
pls hurry = 50 point
Answers
Answer:
the answer is b, c, d, a, respectively
I WILL MARK U BRAINLIEST IF U DO THIS CORRECTLY!!!!!! ATTACHMENT BELOW

Answers
Answer:
210
Step-by-step explanation:
If each floor was 14 ft, and they want 15 floors, you would do 14 x 15, which equals 210
What is the Total number of Outcomes for a family of 3 with having boys and girls?
Answers
There are 8 possible outcomes, all equally likely (if we assume each gender is equally likely). Hence the choice is 3/8. We can also think about it in at least one more way: You identified all the possible ways to get 2 boys and one girl.
Does anyone know this?

Answers
Answer:
i think c or b I D K
Step-by-step explanation:
Find the area of the composite figure below.
2 ft
2 ft
6 ft
4 ft
8 ft
22 ft2
30 st²
36 ft²
38 ft
Answers
Answer:
A = 139.25
Step-by-step explanation:
There was 3/5 of a gallon of paint in the bucket. Dr. Wu used 2/5 of that. How much paint was left?
Answers
Answer:
1/5
Step-by-step explanation:
equation: 3/5-2/5=x
we can multiply the whole equation by 5 so that we can easily subtract the numbers
3-2=1
now we divide it by 5 so that we get our number in a fraction
after we divide we get 1/5
What is the complementary angle of CFB

Answers
Step-by-step explanation:
CFB reads as twenty five degrees
complementary angle will add to it to sum 90 degrees = sixty five degrees
angle CFD is sixty five degrees
A line passes through the point (2,−4) and has a slope of 1/2. What is the y-coordinate of the point on the line when x = 8?
A. −1
B. 7
C. −2
D. 8
E. 5
Answers
The y-coordinate of the point on the line when x = 8 is -1
What are linear equations?Linear equations are equations that have constant average rates of change. Note that the constant average rates of change can also be regarded as the slope or the gradient
What is the y-coordinate of the point on the line when x = 8?The given parameters are
Slope, m = 1/2
Point, (x1, y1) = (2, -4)
The linear equation is calculated as
y = m(x - x1) + y1
So, we have
y = 1/2(x - 2) - 4
When x = 8, we have
y = 1/2(8 - 2) - 4
Evaluate
y = -1
Hence, the y-coordinate of the point on the line when x = 8 is -1
Read more about linear equations at
https://brainly.com/question/1884491
#SPJ1
need help with this ASAP
!!!!!!!!!!!!!!!!!!!!!!!!

Answers
The fence in dead center is about 399 feet from the third base.
What is the Pythagorean Theorem?The Pythagorean Theorem states that in the case of a right triangle, the square of the length of the hypotenuse, which is the longest side, is equals to the sum of the squares of the lengths of the other two sides.
Hence the equation for the theorem is given as follows:
c² = a² + b².
In which:
c > a and c > b is the length of the hypotenuse.a and b are the lengths of the other two sides (the legs) of the right-angled triangle.For the triangle in this problem, we have that:
The sides are d ft and 90 ft.The hypotenuse is of 409 ft.Hence the distance is obtained as follows:
d² + 90² = 409²
\(d = \sqrt{409^2 - 90^2}\)
d = 399 ft.
More can be learned about the Pythagorean Theorem at brainly.com/question/30203256
#SPJ1
The sum of three numbers is 49. The second number is five less than three times the third number. If the first number is twice the amount of the third number, what is the value of the second number?
Answers
Answer:
(x, y, z) → (18, 22, 9)
Step-by-step explanation:
sum of three numbers is 49
x + y + z = 49
second number is 5 less than three times the third number
y = 3z - 5
first number is twice amount of third number
x = 2z
set of equations
x + y + z = 49
y = 3z - 5
x = 2z
plug in 2nd and 3rd equation into first
(2z) + (3z - 5) + z = 49
combine like terms
2z + 3z - 5 + z = 49
6z - 5 = 49
add 5 to both sides
6z = 54
divide by 6
z = 9
plug z into 2nd and 3rd equations
y = 3(9) - 5
y = 27 - 5
y = 22
x = 2(9)
x = 18
check:
18 + 22 + 9 = 49
(x, y, z) → (18, 22, 9)
A cylinder has a height of 16 inches and a diameter of 34 inches. What is its volume? Use ≈ 3.14 and round your answer to the nearest hundredth.
Answers
We are given that:
Height of cylinder = 16 inches Diameter of cylinder = 34 inches We have to use π = 3.14Ⳙ⳽ⲓⲛⳋ ⳨ⲟⲅⲙⳙⳑɑ:
Since, cylinder has circular ends , it's volume is given by the formula:
\( \quad\hookrightarrow\quad {\pmb{\sf { \pi r^2 h }} }\)
Ⲧⲏⲉⲅⲉ⳨ⲟⲅⲉ:
\( \quad :\implies\quad \sf {V = \pi r^2 h }\)
\( \quad :\implies \quad \sf { V =\pi\left( \cancel{\dfrac{34}{2}}\right)^2\times 16}\)
\( \quad :\implies\quad \sf {V = 3.14 \times (17)^2 \times 16 }\)
\( \quad :\implies\quad \sf { V = 3.14\times 289 \times 16}\)
\( \quad :\implies \quad{\pmb{ \sf {V = 14,519.36}} }\)
ㅤㅤ ㅤㅤ~Hence, the volume of given cylinder is 14,519.36 cube inches.
please i’ll fail if i don’t get this right. please i’ll give brainlyist The current temperature of 15°F below zero is 18°F below the high temperature of the day. What is the high temperature for the
day?
OA. 5°F
ов. 33°F
OC. 3°F
OD. 33°F
Answers
Answer:
I think its C
Step-by-step explanation:
BRUH NO ONE EVER ANSWERS MY QUESTONS UNTIL A MONTH OR WEEKS LATER WHEN I DONT NEED IT
3u^2+v=69 which values of u and v make it true
A. u=-5 and v=-7
B. u=5 and v=7
C. u=-5 and v=6
D. u=-5 and v=-6
Answers
Answer:
B hope this helped
Step-by-step explanation:
You received a Score Of 3.4 on your annual review. Merit increases are given out starting at 0.5% at a score of 2.6 and it goes up 1% every 0.4 points. So, I will be receiving an increase of what?
Answers
Based on your annual review score of 3.4, you would receive a merit increase of 2.5%.
To determine the merit increase based on your annual review score of 3.4, we need to calculate the increase increment based on the given scale.
First, we need to determine the number of 0.4-point increments between your score of 3.4 and the baseline score of 2.6, which is the starting point for merit increases. The difference is 3.4 - 2.6 = 0.8.
Since the merit increases go up by 1% for every 0.4 points, we divide the difference of 0.8 by 0.4 to find the number of 0.4-point increments:
0.8 / 0.4 = 2
So, there are 2 increments of 0.4 points.
Next, we calculate the merit increase percentage. The baseline increase is 0.5%, and it increases by 1% for each 0.4-point increment. Since we have 2 increments, the increase percentage would be:
0.5% + 2 * 1% = 0.5% + 2% = 2.5%
Therefore, based on your annual review score of 3.4, you would receive a merit increase of 2.5%.
It's important to note that this calculation assumes a linear progression of merit increases based on the given criteria. The actual merit increase policy may vary depending on company practices and policies.
For more such question on annual review score visit:
https://brainly.com/question/28641970
#SPJ8
What is the area of the square that measures 3.1 m on each side
Answers
The area of the square with a side length of 3.1 meters is 9.61 square meters.
To find the area of a square, we need to multiply the length of one side by itself. In this case, the square has a side length of 3.1 m.
Area of a square = side length × side length
Substituting the given side length into the formula:
Area = 3.1 m × 3.1 m
To perform the calculation:
Area = 9.61 m²
It's worth noting that when calculating the area, we are working with squared units. In this case, the side length is in meters, so the area is expressed in square meters (m²). The area represents the amount of space enclosed within the square.
Remember, to find the area of any square, you simply need to multiply the length of one side by itself.
The area of the square with a side length of 3.1 meters is 9.61 square meters.
For more such questions on square
https://brainly.com/question/27307830
#SPJ8
5x + 4 = 3x + 10 how would you solve for the value of x? How would you prove your solution is correct? How would you prove another value is incorrect? Explain in as much detail as possible.
Answers
5x+3=3x+10 the first thing we're going to do it to subtract 3 from both sides which would look like this
5x+3-3x=10 (the minus because it changed place)
from 5x and 3x we get 2x so the next step is 2x=10-3 which is 7
so now we have
2x=7
x=7/2
Answer:
x=3
Step-by-step explanation:
5x+4 = 3x+10
2x = 6
therefore, x = 3
Verification:
5 * 3 + 4 = 3 * 3 + 10
15+4 = 9+10
19=19
Therefore, LHS= RHS
Hence Proved!
Find LN, given that M lies between L and N, LM = 22 and MN = 6
Answers
Answer:
LN=28
Step-by-step explanation:
If the distance between L and M is 22 and the distance between M and N is 6, and M is between L and N, you would add 22+6 and get 28
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
Determine whether u and v are orthogonal.
u = (-1,3,-1) v = (2,-1,5)
Answers
===================================================
Explanation:
We compute the dot product. This is where we multiply corresponding coordinates and add the products.
If
u = (a,b,c)
v = (d,e,f)
then
u dot v = a*d + b*e + c*f
If the result of the dot product is zero, then the vectors are orthogonal.
---------------
So,
u dot v = a*d + b*e + c*f
u dot v = -1*2 + 3*(-1) + (-1)*5
u dot v = -2-3-5
u dot v = -10
The result is nonzero.
It tells us that these vectors are not orthogonal.
The two vectors do not form a 90 degree angle.
What is the vertex of the graph of the function f(x) = x2 + 8x − 2 ? (−4, 18) (0, -2) (-8, -2) (−4, −18)
Answers
Answer:
(−4, −18)
Step-by-step explanation:
f(x) = x^2 + 8x - 2
⇒ CONVERT TO VERTEX FORM
≥ f(x) = (x + 4)^2 - 16 - 2
≥ f(x) = (x + 4)^2 - 18
⇒ VERTEX IS AT:
≅ ((−4, −18))
Answer:
The answer is D......
Step-by-step explanation:
This pattern follows the rule add 7, then subtract 3. What are the next two numbers?
19, 23, 27, ________, ________
Group of answer choices
31, 35
31, 38
34, 35
Answers
31 and 35.
Sure hope this helps you
A fast food restaurant was selling 7 boxes of chicken nuggets for $25.90.
A competing restaurant was selling 3 boxes of chicken fingers for $11.07.
Which food has a higher unit price?
Answers
the axis of symmetry for the graph of the function f(x)=1/4x2+bx+10 is x=6 what is the vale of 6?
Answers
Considering the vertex of the quadratic equation, it is found that the value of b is of b = 3.
What is the vertex of a quadratic equation?A quadratic equation is modeled by:
y = ax^2 + bx + c
The vertex is given by:
\((x_v, y_v)\)
In which:
\(x_v = -\frac{b}{2a}\)\(y_v = -\frac{b^2 - 4ac}{4a}\)The axis of symmetry is of \(x = x_v\). In this problem, we have that a = 0.25 and x_v = 6, hence:
b/2a = 6.
b/0.5 = 6
b = 6 x 0.5
b = 3.
The value of b is of b = 3.
More can be learned about the vertex of a quadratic equation at https://brainly.com/question/24737967
#SPJ1
suppose six of these people are men, and the other six are women. in how many ways can they join hands for a circle dance, assuming they alternate in gender around the circle
Answers
Twelve people join hands for a circle dance.In how many ways can they do this? Suppose six of these people are men, and the other six are women. In how many ways can they join hands for a circle dance, assuming they alternate in gender around the circle
Answer:
86400 ways
Step-by-step explanation:
Since the circle can be rotated, the number of ways to arrange a distinct number of n objects in a circle will be (n−1)!.
Now, if we rotate the circle with the six women, we will see that there are 5! ways with which they can be placed in the circle.
After picking the places for the women, we will now fill each gap between two women with a man.
We have 6 men. Thus, number of ways to arrange the men is 6!
Thus,number of ways they can join hands for a circle dance, assuming they alternate in gender around the circle = 5! × 6! = 86400 ways
Whoever helps i will be forever grateful u saved my future thanks so much ily

Answers
1. The probability of obtaining a difference of 4 is 1/18.
2. The probability of obtaining a difference of 5 is 1/36
3. The most likely number for the difference is 0.
What are the probabilities?The probabilities are calculated as follows:
Probability = number of expected outcomes/number of possible outcomesa) The probability of obtaining a difference of 4:
There are 2 ways to obtain a difference of 4: spinning 4 and 0 and spinning 5 and 1.
the number of expected outcomes = 2.
the number of possible outcomes is 6 x 6 = 36
probability of obtaining a difference of 4 = 2/36 or 1/18
b) The probability of obtaining a difference of 5:
There is only 1 way to obtain a difference of 5; spinning 5 and 0.
probability of obtaining a difference of 5 = 1/36
c) From the above calculations, the difference with the highest probability is 0, with a probability of 1/9. So, the most likely number for the difference is 0.
Learn more about probability at: https://brainly.com/question/24756209
#SPJ1
Graduation gift of $5,000 average 2.5% interest on the principal. 5. Say you were 18 yrs old when you deposited the money. How much money will be in the account when you withdraw it at the age of 66 years old, assuming it is compounded annually?