Academy sports equipment sore is having a sale on bike helmets and water bottles. One bike club purchased 10 helmets and 2 water bottles for $155. Another bike club purchased 12 helmets and 3 water bottles for $189. Write and solve a system of equations to determine the cost each a helmet and water bottle?
Answers
Answer:
10h + 2b = 155
12h + 3b = 189
Step-by-step explanation:
Hope this helps :D
Related Questions
Peyton wanted to buy a new game. The game costs $65.00 before sales tax. If the sales tax is 8%, how much will she pay for the game?
Answers
Answer:
73
Step-by-step explanation:
please use R programing to solve this problem. and then we can
use sigma=1 for solve this problem.
Weighted least squares method intends to correct for unequal variance in linear re- gression. We can set the weights parameter in the 1m () function to specify the weights of variance. When the weight
Answers
The summary of the model using summary(model), which will provide information about the regression coefficients, standard errors, t-values, and p-values.
To solve the problem using R programming and the weighted least squares method, we can utilize the lm() function with specified weights. Here's an example code snippet to demonstrate the process:
# Define the number of licensed drivers (X) and the number of cars (Y)
drivers <- c(5, 5, 2, 2, 3, 1, 2)
cars <- c(4, 3, 2, 2, 2, 1, 2)
# Create weights based on the assumption of equal variance (sigma = 1)
weights <- rep(1, length(drivers))
# Perform weighted least squares regression
model <- lm(cars ~ drivers, weights = weights)
# Print the summary of the model
summary(model)
In the code snippet above, we first define the vectors drivers and cars to represent the number of licensed drivers (X) and the number of cars (Y) for the houses in your neighborhood.
Next, we create the weights vector and set it to a constant value of 1 for each observation, assuming equal variance (sigma = 1) for all data points.
Then, we use the lm() function to perform the weighted least squares regression. The formula cars ~ drivers specifies that we want to predict the number of cars based on the number of drivers. We pass the weights argument to the function to assign the specified weights to each observation.
Finally, we print the summary of the model using summary(model), which will provide information about the regression coefficients, standard errors, t-values, and p-values.
Running this code will give you the results of the weighted least squares regression analysis, taking into account the specified weights.
Learn more about regression here
https://brainly.com/question/25987747
#SPJ11
1) Consider a circle of radius 5 miles with an arc on the circle of length 3 miles. What would be the measure of the central angle that subtends that arc
Answers
Answer:
Given that a circle of radius 5 miles has an arc of length 3 miles.
The central angle of the arc can be found using the formula:\(\[\text{Central angle} = \frac{\text{Arc length}}{\text{Radius}}\]\)
Substitute the given values into the formula to get:\(\[\text{Central angle} = \frac{3}{5}\]\)
To get the answer in degrees, multiply by 180/π:\(\[\text{Central angle} = \frac{3}{5} \cdot \frac{180}{\pi}\]\)
Simplify the expression:\(\[\text{Central angle} \approx 34.38^{\circ}\]\)
Therefore, the measure of the central angle that subtends the arc of length 3 miles in a circle of radius 5 miles is approximately 34.38 degrees.
Central angle: https://brainly.com/question/1525312
#SPJ11
A mathematical combination of numbers and letters that result in the desired answer is called a:_________
Answers
A mathematical combination of numbers and letters that result in the desired answer is called an algebraic expression.
Expression:
An expression contains minimum of two terms containing numbers or variables, or both, connected by an operator in between. The mathematical operators can be of addition, subtraction, multiplication, or division.
Given:
A mathematical combination of numbers and letters that result in the desired answer is called.
Here we need to find the term that is suitable for this definition.
Here the answer is algebraic expression.
Basically, the algebraic expression is the combinations of variables , numbers, and at least one arithmetic operation.
For example,
2x + 3y = 5
Where
x and y are variables
2,3 are coefficients of ax and y
5 is the constant
+ and = are the arithmetic operators.
To know more about Expressions here
https://brainly.com/question/13947055
#SPJ4
how to solve 1.6 ×0.215
Answers
Answer:
35.344
Step-by-step explanation:
what does the equation x 2 y 2 = 4 correspond to if a) x, y are the only variables being considered, b) x, y, z are the only variables being considered.
Answers
The equation x² y² = 4 corresponds to a hyperbola when only considering x and y as variables. When considering x, y, and z as variables, the equation corresponds to a two-sheeted hyperboloid.
a) When only x and y are the variables being considered, the equation x² y² = 4 corresponds to a circle in the xy-plane. The circle has a center at the origin (0,0) and a radius of 2.
b) If x, y, and z are the only variables being considered, the equation x² y² = 4 still represents a circle in the xy-plane, but it becomes a cylinder along the z-axis. This cylinder has a center on the z-axis and a radius of 2, extending infinitely along the z-axis.
To know more about hyperbola visit:
https://brainly.com/question/27799190
#SPJ11
You have a mortagege of $275,000
after down payment with an interest
rate of 3% for 30 years.
What does P, r,n, and t are equal to?

Answers
Answer:
Our calculator limits your interest deduction to the interest payment that would be paid on a $1,000,000 mortgage. Interest rate: Annual interest rate for this
Step-by-step explanation:
how do I find the area of the composite figure?
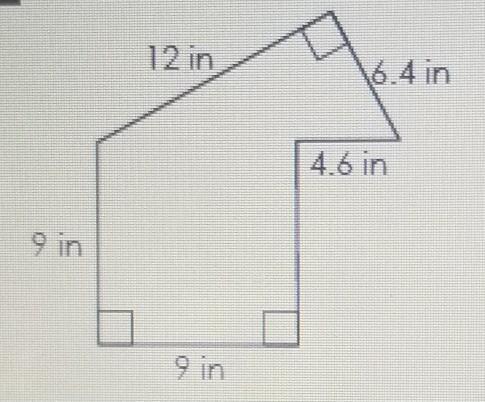
Answers
A = 119.4in^2
hope it's helpful ❤❤❤❤
THANK YOU.

how many sequences of 0s and 1s of length 19 are there that begin with a 0, end with a 0, contain no two consecutive 0s, and contain no three consecutive 1s? (2019 amc 10 b)
Answers
There are 65, 19-bit sequences of 0s and 1s that start with a 0 and end with a 0 that exist.
Explain the term sequences?A grouping of numbers in such a specific order is known as a sequence. On the other perspective, a series is described as the accumulation of a sequence's constituent parts.Any subsequent 0 in the sequence must come exactly two or three spots down from the previous one.
We begin at point 1 and finish at position 19 in this instance.
That is, we advance along the line a whole of 18 positions.
In order to achieve 18, we must add all series consecutive 2s and 3s.
There are numerous methods for doing this:
Case 1: There is just one possible arrangement for nine 2s.
Case 2: Two 3s with six 2s - thus ⁸C₂ ways = 28 ways
Case 3: Four 3s with three 2s - thus ⁷C₄ ways = 35 ways
Case 4: Six 3s - Only 1 way to arrange.
Thus, the number of arrangements = 1 + 28 + 35 + 1 = 65 .
Therefore ,the total possible number of the sequence that cane be made is 65 .
To know more about the sequences, here
https://brainly.com/question/7882626
#SPJ4
A wallet contains 2 quarters and 3 dimes. Clara selects one coin from the wallet, replaces it, and then selects a second coin. Let A = {the first coin selected is a quarter}, and let B = {the second coin selected is a dime}. Which of the following statements is true?
a. A and B are dependent events, as P(B|A) = P(B).
b. A and B are dependent events, as P(B|A) ≠ P(B).
c. A and B are independent events, as P(B|A) = P(B).
d. A and B are independent events, as P(B|A) ≠ P(B).
Answers
Therefore, the correct statement is d. A and B are independent events, as P(B|A) ≠ P(B).
To determine whether events A (the first coin selected is a quarter) and B (the second coin selected is a dime) are dependent or independent, we need to compare the conditional probability P(B|A) with the probability P(B).
Let's calculate these probabilities:
P(B|A) is the probability of selecting a dime given that the first coin selected is a quarter. Since Clara replaces the first coin back into the wallet before selecting the second coin, the probability of selecting a dime is still 3 out of the total 5 coins in the wallet:
P(B|A) = 3/5
P(B) is the probability of selecting a dime on the second draw without any information about the first coin selected. Again, since the wallet still contains 3 dimes out of 5 coins:
P(B) = 3/5
Comparing P(B|A) and P(B), we see that they are equal:
P(B|A) = P(B) = 3/5
According to the options given:
a. A and B are dependent events, as P(B|A) = P(B). - This is incorrect as P(B|A) = P(B) does not necessarily imply independence.
b. A and B are dependent events, as P(B|A) ≠ P(B). - This is also incorrect because P(B|A) = P(B) in this case.
c. A and B are independent events, as P(B|A) = P(B). - This is incorrect because P(B|A) = P(B) does not imply independence.
d. A and B are independent events, as P(B|A) ≠ P(B). - This is the correct statement because P(B|A) ≠ P(B).
To know more about independent events,
https://brainly.com/question/16229941
#SPJ11
Dorothy is trying to estimate 20. She uses this table of values:
Square 4.02 4.12 4.22 4.32 4.42 4.52
Value
16.0 16.8 17.6 18.5 19.4 20.3
Square 4.62 4.72 4.82 4.92 5.02
Value
21.2 22.1 23.0 24.0 25.0
What should she do next to find 20 to the nearest hundredth?
O A. She should estimate that 20 is 4.50.
B. She should find the average of 4.4 and 4.5.
O C. She should find the squares of numbers between 4.5 and 4.6.
D. She should find the squares of numbers between 4.4 and 4.5.

Answers
Answer:
D
Step-by-step explanation:
im taking the test for math on apex
Answer:
Step-by-step explanation:
The nice correct answer is D your welcome
18 1 point Suppose a random sample of 84 men has a mean foot length of 26.9 cm with a standard deviation of 2.1 cm. What is an 95% confidence interval for this data? 24.8 to 29 21.52 to 32.28 24.905 t
Answers
A confidence interval is an estimate of an unknown population parameter. It is a range of values, derived from a statistical model, that contains the true value of the parameter with a certain degree of confidence.
In the given problem, we are supposed to find a 95% confidence interval for the data.
We are given the following data:
Sample size \((n) = 84 Mean (x) = 26.9 cm\)
Standard deviation \((s) = 2.1 cm\)
Confidence level = 95%
To find the 95% confidence interval, we will use the formula:
Confidence interval \(= x ± z * (s / sqrt(n))\)
Here, x is the sample mean, s is the sample standard deviation, n is the sample size, and z is the z-score corresponding to the given confidence level. For a 95% confidence level, the z-score is 1.96 (approx.)
Let's put the given values in the formula:
Confidence interval \(= 26.9 ± 1.96 * (2.1 / sqrt(84))\) Simplifying this expression, we get:
Confidence interval = 26.9 ± 0.4548
Hence, the 95% confidence interval for the given data is
\((26.9 - 0.4548, 26.9 + 0.4548)\)
which gives us the range of \((26.4452, 27.3548)\).
To know more about confidence interval visit:
https://brainly.com/question/32546207
#SPJ11
ANSWER ASAP!
what is the value of a₁₇ if a₁₃=26 and the recursive form of a geometric sequence is aₙ=1/2aₙ₋₁
please answer with atleast some detail
Answers
The 17th term of the geometric sequence given in the problem is:
\(a_{17} = \frac{13}{8}\)
What is a geometric sequence?A geometric sequence is a sequence in which the result of the division of consecutive terms is always the same, called common ratio q.
The nth term of a geometric sequence is given by:
\(a_n = a_1q^{n-1}\)
In which \(a_1\) is the first term.
As a function of the mth term, the nth term can also be given as follows:
\(a_n = a_mq^{n - m}\)
In this problem, we have that:
\(a_{13} = 26, q = \frac{1}{2}\)
Hence the 17th term is:
\(a_{17} = a_{13}q^{4}\)
\(a_{17} = 26 \times \frac{1}{16}\)
\(a_{17} = \frac{13}{8}\)
More can be learned about geometric sequences at https://brainly.com/question/11847927
#SPJ1
Which of the equations are linear equations? Explain reasoning.
5x − 4y = 3
3x + 3y = 2
2x2−4y2=11
Answers
Answer:
5x - 4y = 3 and 3x + 3y = 2 are linear equations.
Step-by-step explanation:
Linear equations:
Linear equations are algebraic equations with highest power of the variable 1.
So, 5x - 4y = 3 and 3x + 3y = 2 are linear equations.
f-1(x) = (3х – 5)2 + 12
Answers
Answer:
i think its 3 if im not mistaken
Step-by-step explanation:
What is the slope of the line that passes through the points (7, -4) and (7, 0)? Write your answer in simplest form.
Answers
Answer:
Step-by-step explanation:
x1=7 ,y1=-4 ,x2=7 ,y2=0
By using Two-points form:
\(\frac{y-y_{1}}{y_{2}-y_{1} } =\frac{x-x_{1} }{x_{2}-x_{1} }\)
Substitute values:
\(\frac{y+4}{0+4} =\frac{x-7}{7-7}\)
\(\frac{y+4}{4} =\frac{x-7}{0}\)
4(x-7)=0(y+4)
4(x-7)=0
x-7=0
x-7=0 is the line parallel to y-axis at point x=7.
If you need to ask any question, please let me know.
Suppose you calculated a paired-samples t test, with 30 pairs of scores. Mean mean difference is 6 and the standard error is 2.1. What is the .95 confidence interval
Answers
This means that we can be 95% confident that the true population means difference lies between 1.7075 and 10.2925.
Confidence interval = Mean difference ± (t-value × standard error)
Substituting the given values into the formula, we get:
Confidence interval = 6 ± (2.045 × 2.1)
Confidence interval = 6 ± 4.2925
A confidence interval is a statistical concept used to estimate the range of values in which a population parameter is likely to fall. It is calculated using sample data and is used to provide an estimate of the true population parameter.
The confidence interval is a range of values that is constructed around a point estimate, such as the sample mean or proportion. This range is based on the level of confidence chosen by the researcher, typically 90%, 95%, or 99%. For example, a 95% confidence interval means that if we were to repeat the sampling process many times, we would expect the true population parameter to fall within the range of values calculated for 95% of those samples.
To learn more about Confidence intervals visit here:
brainly.com/question/24131141
#SPJ4
What is the degree of each polynomial 4m2-3m6+5m4
Answers
The answer to the given question about degree of polynomial is polynomial 4m² - 3m⁶ + 5m⁴ has a degree of 6.
The degree of a polynomial is the highest power of the variable in the polynomial. In the given polynomial 4m² - 3m⁶ + 5m⁴, the highest power of the variable 'm' is 6, which is the degree of the polynomial. Therefore, the degree of the polynomial 4m² - 3m⁶ + 5m⁴ is 6. Polynomials are algebraic expressions consisting of one or more terms involving variables with non-negative integer exponents. The degree of a polynomial is the highest power of the variable in the polynomial. The degree of a polynomial is an essential concept in algebra, as it helps to determine the behavior of the polynomial under various operations such as addition, subtraction, multiplication, and division. A polynomial of degree n can have at most n distinct roots or solutions. The degree of a polynomial is also used to determine the end behavior of the polynomial function. The higher the degree of the polynomial, the more complex its behavior can be.
To learn more about polynomial function click here
brainly.com/question/12914312
#SPJ4
Solve the following difference equation where x(k) is a discrete unit step input and y(k) is the system output.
y(k) − y(k − 1) + 0.24y(k − 2) = x(k) + x(k + 1)
Answers
the solution to the given difference equation is y(k) = \(0.2^k\) - 2.4 * \(1.2^k\)
To solve the given difference equation, we can use the Z-transform method. Let's denote the Z-transform of a function y(k) as Y(z), and the Z-transform of x(k) as X(z).
Applying the Z-transform to the given equation and using the properties of linearity, time shifting, and the Z-transform of the unit step function, we have:
z²Y(z) - zY(z) + 0.24Y(z) = (z + 1)X(z)
Next, we can rearrange the equation to solve for Y(z):
Y(z)(z² - z + 0.24) = (z + 1)X(z)
Dividing both sides by (z² - z + 0.24), we get:
Y(z) = (z + 1)X(z) / (z² - z + 0.24)
Now, we need to find the inverse Z-transform of Y(z) to obtain the time-domain solution y(k). To do this, we can use partial fraction decomposition and lookup tables to find the inverse Z-transform.
The denominator of Y(z), z² - z + 0.24, can be factored as (z - 0.2)(z - 1.2). We can then rewrite Y(z) as:
Y(z) = (z + 1)X(z) / [(z - 0.2)(z - 1.2)]
Now, we perform partial fraction decomposition to express Y(z) as:
Y(z) = A / (z - 0.2) + B / (z - 1.2)
To find the values of A and B, we can multiply both sides of the equation by the common denominator:
(z - 0.2)(z - 1.2)Y(z) = A(z - 1.2) + B(z - 0.2)
Expanding and equating coefficients, we have:
z²Y(z) - 1.4zY(z) + 0.24Y(z) = Az - 1.2A + Bz - 0.2B
Now, we can equate the coefficients of corresponding powers of z:
Coefficient of z²: 1 = A
Coefficient of z: -1.4 = A + B
Coefficient of z⁰ (constant term): 0.24 = -1.2A - 0.2B
Solving these equations, we find A = 1, B = -2.4.
Substituting these values back into the partial fraction decomposition equation, we have:
Y(z) = 1 / (z - 0.2) - 2.4 / (z - 1.2)
Now, we can use the inverse Z-transform lookup tables to find the inverse Z-transform of Y(z):
y(k) = Z⁻¹{Y(z)} = Z⁻¹{1 / (z - 0.2) - 2.4 / (z - 1.2)}
The inverse Z-transform of 1 / (z - 0.2) is given by the formula:
Z⁻¹{1 / (z - a)} = \(a^k\)
Using this formula, we get:
y(k) = \(0.2^k\) - 2.4 * \(1.2^k\)
Therefore, the solution to the given difference equation is y(k) = \(0.2^k\) - 2.4 * \(1.2^k\)
Learn more about Z-transform method here
https://brainly.com/question/14979001
#SPJ4
The effectiveness of a blood-pressure drug is being investigated. An experimenter finds that, on average, the reduction in systolic blood pressure is 60.2 for a sample of size 812 and standard deviation 20.8. Estimate how much the drug will lower a typical patient's systolic blood pressure (using a 80% confidence level). Enter your answer as a tri-linear inequality accurate to one decimal place (because the sample statistics are reported accurate to one decimal place). <μ< Answer should be obtained without any preliminary rounding.
Answers
Using a sample size of 812, a standard deviation of 20.8, and an 80% confidence level, the estimated range for the reduction in systolic blood pressure caused by the drug is approximately 59.3 to 61.1 units.
Using the given sample size, standard deviation, and confidence level, we can estimate the reduction in systolic blood pressure caused by the drug. The estimated range for the reduction is given as a trilinear inequality, without preliminary rounding.
To estimate the reduction in systolic blood pressure caused by the drug at a confidence level of 80%, we can use a confidence interval. The formula for the confidence interval is:
CI = X(bar) + or - Z * (σ/√n)
Where:
- X(bar) is the sample mean (average reduction in systolic blood pressure),
- Z is the z-score corresponding to the desired confidence level (80% confidence corresponds to a z-score of approximately 1.282),
- σ is the standard deviation of the sample (20.8),
- n is the sample size (812).
Plugging in the values, we can calculate the confidence interval as:
CI = 60.2 + or - 1.282 * (20.8/√812)
Simplifying the expression, we find:
CI = 60.2 ± 1.282 * 0.729
Calculating the values, we have:
CI = 60.2 + or - 0.935
Therefore, the estimated range for the reduction in systolic blood pressure caused by the drug, at an 80% confidence level, is approximately 59.3 to 61.1. This means that we can estimate with 80% confidence that the drug will lower a typical patient's systolic blood pressure by an amount between 59.3 and 61.1 units.
To learn more about standard deviation click here: brainly.com/question/29115611
#SPJ11
FIND THE VOLUME OF EACH FIGURE THANK UUU

Answers
Answer:
32
Step-by-step explanation:
help please this is due rn

Answers
37 A grocery store clerk arranged 72 boxes of pasta on 3 shelves. If he placed the same number of boxes on each shelf, how many boxes did he place on
each shelf?
Answers
Answer:
24.
Step-by-step explanation:
The answer to this can be found by dividing 72 by 3.
72 divided by 3 = 24.
IT'S DUE TODAY please some1 help me on this one.
In ΔQRS, s = 5.2 inches, ∠S=129° and ∠Q=30°. Find the length of r, to the nearest 10th of an inch.
Answers
Answer:
Q+R+S=180
30°+R+129°=180
R=180-159
R=21..
is the answer
A recent study was funded to explore if there was an association between cell phone use the prostate cancer. A random cohort of males was sampled who aged from 25 to 85 years old. We found that among the 5,643 men who had prostate cancer, 1,749 had high cell phone usage (as opposed to low/normal cell phone usage), while among the 11,234 men who did not have prostate cancer, 3,439 had high cell phone usage.
a) Calculate the point estimate of the odds ratio and interpret it.
b) Is there an association with cell phone usage and prostate cancer? In other words, conduct a hypothesis test to determine if the odds ratio significantly differ from 1?
Answers
a) The point estimate of the odds ratio is approximately 1.021. This means that the odds of having prostate cancer among individuals with high cell phone usage are about 1.021 times the odds of having prostate cancer among individuals with low/normal cell phone usage.
b) Based on the significance level chosen (e.g., α = 0.05), if the calculated chi-square value is greater than the critical chi-square value, we reject the null hypothesis and conclude that there is a significant association between cell phone usage and prostate cancer.
a) To calculate the point estimate of the odds ratio, we use the following formula:
Odds Ratio = (ad/bc)
Where:
a = Number of individuals with both prostate cancer and high cell phone usage (1,749)
b = Number of individuals without prostate cancer but with high cell phone usage (3,439)
c = Number of individuals with prostate cancer but low/normal cell phone usage (5,643 - 1,749 = 3,894)
d = Number of individuals without prostate cancer and low/normal cell phone usage (11,234 - 3,439 = 7,795)
Substituting the values, we have:
Odds Ratio = (1,749 * 7,795) / (3,439 * 3,894)
= 13,640,755 / 13,375,866
≈ 1.021
Interpretation:
The point estimate of the odds ratio is approximately 1.021. This means that the odds of having prostate cancer among individuals with high cell phone usage are about 1.021 times the odds of having prostate cancer among individuals with low/normal cell phone usage.
However, further analysis is needed to determine if this difference is statistically significant.
b) To determine if the odds ratio significantly differs from 1, we can conduct a hypothesis test using the chi-square test.
The null hypothesis (H0) states that there is no association between cell phone usage and prostate cancer, while the alternative hypothesis (Ha) states that there is an association.
The test statistic for the chi-square test is calculated as:
Chi-square = [(ad - bc)^2 * (a + b + c + d)] / [(a + b)(c + d)(b + d)(a + c)]
Using the given values, we can substitute them into the formula:
Chi-square = [(1,749 * 7,795 - 3,439 * 3,894)^2 * (1,749 + 3,439 + 3,894 + 7,795)] / [(1,749 + 3,439)(3,894 + 7,795)(3,439 + 7,795)(1,749 + 3,894)]
After calculating the numerator and denominator, the test statistic is obtained. This value is then compared to the chi-square distribution with one degree of freedom to determine its significance.
Based on the significance level chosen (e.g., α = 0.05), if the calculated chi-square value is greater than the critical chi-square value, we reject the null hypothesis and conclude that there is a significant association between cell phone usage and prostate cancer.
Otherwise, if the calculated chi-square value is less than the critical chi-square value, we fail to reject the null hypothesis, indicating no significant association.
Unfortunately, without the specific chi-square value calculated, a definitive conclusion cannot be interpreted.
To know more about chi-square refer here :
https://brainly.com/question/31871685
#SPJ11
let the ratio of two numbers x+1/2 and y be 1:3 then draw the graph of the equation that shows the ratio of these two numbers.
Answers
Step-by-step explanation:
since there is no graph it's a bit hard to answer this question, but I'll try. I can help solve the equation that represents the ratio of the two numbers:
(x + 1/2)/y = 1/3
This can be simplified to:
x + 1/2 = y/3
To graph this equation, you would need to plot points that satisfy the equation. One way to do this is to choose a value for y and solve for x. For example, if y = 6, then:
x + 1/2 = 6/3
x + 1/2 = 2
x = 2 - 1/2
x = 3/2
So one point on the graph would be (3/2, 6). You can choose different values for y and solve for x to get more points to plot on the graph. Once you have several points, you can connect them with a line to show the relationship between x and y.
(Like I said, it was a bit hard to answer this question, so I'm not 100℅ sure this is the correct answer, but if it is then I hoped it helped.)
Use the distributive property to expand 0.05(50 + 40).
Answers
Answer:
4.5
Step-by-step explanation:
Here's what I found on google about distributive property:
To “distribute” means to divide something or give a share or part of something. According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.
Now for the math-
distribute the numbers- 0.05(50)+0.05(40)
solve- 0.05*50= 2.5
0.05*40= 2
2.5+2= 4.5
Hope this helps
Answer:
0.05(50)+0.05(40)
Step-by-step explanation:
Please help with this math problem!!! Will give brainliest!!! :)
A cylindrical grain silo has just been built. The diameter of the silo is 15 feet and the height is 25 feet. How many cubic feet of grain can the silo hold? Round to 2 decimal places.
Answers
Step-by-step explanation:
Use the formula for the volume of a cylinder
volume = pi r^2 h diameter = 15 ft so r, radius = 7.5 feet h = 25 ft
volume = pi * ( 7.5)^2 * 25 = 4417.86 ft^3
The logarithm form of 5^3 =125 is equal to
a. log5 125 = 3 b. log5 125 = 5
c. log3 125 = 5 d. log5 3 = 3
Answers
The correct logarithm form is: a. log5 125 = 3
Question is about finding the logarithm form of 5³ = 125 using the given options.
The correct logarithm form is:
a. log5 125 = 3
Here's the step-by-step explanation:
1. The exponential form is given as 5³= 125.
2. To convert it to logarithm form, you have to express it as log(base) (argument) = exponent.
3. In this case, the base is 5, the argument is 125, and the exponent is 3.
4. Therefore, the logarithm form is log5 125 = 3.
To learn more about logarithm
https://brainly.com/question/12603491
#SPJ11
using dijkstra’s algorithm, find the sink tree rooted at vertex 7.
Answers
Dijkstra's algorithm calculates the shortest path from vertex 7 to all other vertices in the graph, forming a tree structure where vertex 7 is the root.
Dijkstra's algorithm is a graph traversal algorithm used to find the shortest path between two vertices in a weighted graph. To find the sink tree rooted at vertex 7, we can apply Dijkstra's algorithm starting from vertex 7. The algorithm proceeds by iteratively selecting the vertex with the smallest distance from the current set of vertices and updating the distances to its adjacent vertices.
Starting from vertex 7, we initialize the distance of vertex 7 as 0 and the distances of all other vertices as infinity. Then, we explore the adjacent vertices of vertex 7 and update their distances accordingly. We repeat this process, selecting the vertex with the smallest distance each time, until we have visited all vertices in the graph.
The result of applying Dijkstra's algorithm to find the sink tree rooted at vertex 7 is a tree structure that represents the shortest paths from vertex 7 to all other vertices in the graph. Each vertex in the tree is connected to its parent vertex, forming a directed acyclic graph. This sink tree provides a clear visualization of the shortest paths and their corresponding distances from vertex 7 to each vertex in the graph.
Learn more about acyclic graph here:
https://brainly.com/question/31861982
#SPJ11