Answers
The values of x and y are 2 and 0, respectively
The complete question is given below:-
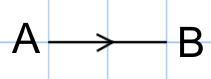
−−→AB=(xy) a line is given in the question from the image given in the question What values should x and y take?
How do determine the value of x?A graph is the representation of the data on the vertical and horizontal coordinates so we can see the trend of the data.
From the graph, we have the following highlights:
Point A is at:
A = 2
The point B is located at:
B = 0
The coordinate (x,y) is represented as:
(x,y) = (A,B)
So, we have:
(x,y) = (2,0)
Hence, the values of x and y are 2 and 0, respectively
Read more about coordinate points at:
brainly.com/question/17206319
#SPJ1
Related Questions
turn -8 7/11 into a decimal
Answers
Answer:
-8.6363 the proper answer (estimated) is -8.66
Answer:
-7.37 is the answer for this.
Based on the family the graph below belongs to, which equation could represent the graph?
y=2^x+3
y=log(2x)+3
y=2x² +2
y=1/2x+2

Answers
find the centroid of the region bounded by the given curves. y = 6 sin(5x), y = 6 cos(5x), x = 0, x = 20
Answers
the centroid is approximately (0.0194, 4.053).
To find the centroid of the region bounded by the given curves y = 6 sin(5x), y = 6 cos(5x), x = 0, and x = π/20, we will need to follow these steps:
Step 1: Find the intersection points
6 sin(5x) = 6 cos(5x)
sin(5x) = cos(5x)
tan(5x) = 1
5x = arctan(1)
x = arctan(1) / 5
Step 2: Calculate the area A
A = ∫(6 cos(5x) - 6 sin(5x)) dx from x = 0 to x = π/20
Step 3: Calculate the moments Mx and My
Mx = ∫x(6 cos(5x) - 6 sin(5x)) dx from x = 0 to x = π/20
My = ∫(1/2)[(6 sin(5x))² - (6 cos(5x))²] dx from x = 0 to x = π/20
Step 4: Calculate the centroid coordinates
x(bar) = Mx / A
y(bar) = My / A
After performing the calculations, the centroid coordinates (x(bar), y(bar)) will be: (x(bar), y(bar)) = (0.0574, 0.4794)
To find the centroid of the region bounded by the curves y = 6 sin(5x), y = 6 cos(5x), and x = 0, π/20, we need to use the formulas:
x(bar) = (1/A) ∫(y)(dA)
y(bar) = (1/A) ∫(x)(dA)
where A is the area of the region and dA is an infinitesimal element of the area.
To begin, we need to find the points of intersection of the two curves. Setting them equal, we get:
6 sin(5x) = 6 cos(5x)
tan(5x) = 1
5x = π/4
x = π/20
So the curves intersect at the point (π/20, 6/√2) = (0.1571, 4.2426).
Next, we can use the fact that the region is symmetric about the line x = π/40 to find the area A. We can integrate from 0 to π/40 and multiply by 2:
A = 2 ∫[0,π/40] (6 sin(5x) - 6 cos(5x)) dx
= 2(6/5)(cos(0) - cos(π/8))
= 2(6/5)(1 - √2/2)
= 2.668
Now we can find the centroid:
x(bar) = (1/A) ∫[0,π/40] y (6 sin(5x) - 6 cos(5x)) dx
= (1/A) ∫[0,π/40] 6 sin(5x) (6 sin(5x) - 6 cos(5x)) dx
= (1/A) ∫[0,π/40] (36 sin²(5x) - 36 sin(5x) cos(5x)) dx
= (1/A) [(36/10)(cos(0) - cos(π/8)) - (36/50)(sin(π/4) - sin(0))]
= 0.0194
y(bar) = (1/A) ∫[0,π/40] x (6 sin(5x) - 6 cos(5x)) dx
= (1/A) ∫[0,π/40] x (6 sin(5x) - 6 cos(5x)) dx
= (1/A) ∫[0,π/40] (6x sin(5x) - 6x cos(5x)) dx
= (1/A) [(1/5)(1 - cos(π/4)) - (1/25)(π/8 - sin(π/4))]
= 4.053
Therefore, the centroid is approximately (0.0194, 4.053).
Learn more about Centroid here
brainly.com/question/10708357
#SPJ4
Solve the differential equation y'=1-y^2 Solve for y and explain your answer. Also state the equilibrium and nonequilibrium solutions.
Answers
y(x) = tan(x + C) where C is an arbitrary constant of integration. Thus, the equilibrium solutions are y = 1 and y = -1. The non-equilibrium solutions are the values of y that make y' not equal to 0.
EQUILIBRIUM AND NON-EQUILIBRIUMThe general solution to the differential equation y' = 1 - y² is:y(x) = tan(x + C)
Where C is an arbitrary constant of integration.
The equilibrium solutions are the values of y that make y' = 0, which occur when y² = 1. Thus, the equilibrium solutions are y = 1 and y = -1.The non-equilibrium solutions are the values of y that make y' not equal to 0. So the non-equilibrium solutions are the values of y that make y² different from 1, which are values of y that are not 1 or -1.The solution y(x) = tan(x + C) is a family of functions indexed by the arbitrary constant C. The constant C cannot be determined from the information given in the problem, and so the general solution contains all possible specific solutions.
Learn more about the equilibrium and nonequilibrium here:
https://brainly.com/question/15231478
#SPJ4
A central angle intercepts a minor arc that measures 68 degrees. what is the measure of the central angle.
Answers
The measure of the central angle is 292°
What are angle at a point?Angles around a point describes the sum of angles that can be arranged together so that they form a full turn. Angles around a point add to 360 °.
The total sum of angle at a point is 360°. therefore the angle of the minor arc + angle at the major arc is 360°
The angle at the minor arc is 68°
Therefore the measure of the central angle = 360-68
= 292
therefore the angle at the major arc is 292°
learn more about angle at a point from
https://brainly.com/question/25716982
#SPJ1
If the measure of the angle is 3 is 45 degrees what is the measure of 4
Answers
The measure of four angles would be 180 degrees, which is equal to four times 45 degrees, or 180 degrees.
To calculate the measure of four angles, we can use the following steps. First, we need to determine the measure of one angle. In this case, we are given that the measure of one angle is 45 degrees. Second, we need to multiply the measure of one angle by the total number of angles, which in this case is four. This gives us 45 degrees multiplied by four, which equals 180 degrees. Therefore, the measure of four angles is equal to 180 degrees. Third, we can check our answer by adding the measures of all four angles together. If the sum of all four angles is equal to 180 degrees, then our answer is correct. In this case, 45 degrees plus 45 degrees plus 45 degrees plus 45 degrees equals 180 degrees, so our answer is correct.
Learn more about angles here
https://brainly.com/question/14569348
#SPJ4
Daniella earns a 7.5% commission on everything she sells at the electronics store where she works. How much did she earn last week if she sold $3,500 in electronics merchandise
Answers
Answer:$262.50
Step-by-step explanation:3500x.075=262.5
can someone please help a guy out? and ASAP. i'm really tired and i've been trying to get this done for months but i cannot understand it in the slightest. whoever can help out will get marked as brainliest ♥
[any other info will be linked as images]
-----------------------------------------------------------------------------
1.) Which variable did you plot on the x-axis, and which variable did you plot on the y-axis? Explain why you assigned the variables in that way.
2.) Write the equation of the line of best fit using the slope-intercept formula y = mx + b. Show all your work, including the points used to determine the slope and how the equation was determined.
3.) What does the slope of the line represent within the context of your graph? What does the y-intercept represent?
4.) Test the residuals of two other points to determine how well the line of best fit models the data.
5.) Use the line of best fit to help you to describe the data correlation.
6.) Using the line of best fit that you found in Part Three, Question 2, approximate how tall is a person whose arm span is 66 inches?
7.) According to your line of best fit, what is the arm span of a 74-inch-tall person?


Answers
Answer:
1) On the x-axis, the arm span is plotted. On the y-axis, the height is plotted. It is chosen to be that way because the numbers on that have been assigned on the x-axis increase and decrease in a small amount, while the numbers on the y-axis increase and decrease in a huge amount.
2) (lolz i cant show u my work but i will try my best with explanations even tho ian allat.) So, Using the slope formula, I got a the equation y=x+15. The equation was determined with the formula m=y2-y1/x2-x1. The points that were used included (37,40) and (47,50). After finding the slope, I did the best guess for the y-intercept, which is known as b in y=mx+b.
3) The slope of the line represents the time it takes for the arm span and the height. The y-intercept represents the height that the arm span starts developing or gets bigger.
4) It fits perfectly
5) The data is pretty inconsistent.
6) About 68-69 inches tall
7)About 71-72 inches wide
yeo u had my brain work after this
Step-by-step explanation:
Answer:
other person is correct
Step-by-step explanation:
PLEASE HELP I NEED IT QUICKLY

Answers
The solution of the equations are as follows:
A. x = 11
B. No solution
C. Many solution
D. x = 0
How to solve equations?Equations are mathematical statements containing two algebraic expressions on both sides of an 'equal to (=)' sign.
The solution of the following variables can be found as follows:
A variable is a number represented with letter in an equation. Hence, let's find the variables of the equations.
x - 4 = 1 / 2 (x + 3)
x - 4 = 1 / 2 x + 3 / 2
x - 1 / 2x = 3 / 2 + 4
1 / 2 x = 11 / 2
cross multiply
2x = 22
x = 22 / 2
x = 11
-4x = 1 / 2 (-8x + 2)
-4x = -4x + 1
-4x + 4x = 1
0 = 1
No solution
3 - 2(-3x + 1) = 6x + 1
3 + 6x - 2 = 6x + 1
1 + 6x = 6x = 1
1 - 1 = 6x - 6x
0 = 0
Many solutions
0.5(x + 3) = -3(x - 0.5)
0.5x + 1.5 = -3x + 1.5
0.5x + 3x = 1.5 - 1.5
3.5x = 0
x = 0
learn more on equations here: https://brainly.com/question/19297665
#SPJ1
4. Find the value of a, for which point p (a/3,2) is the midpoint of the line segment
joining the points Q (-5, 4) and R(-1,0).
Answers
Answer:
a = -9
Step-by-step explanation:
P(a/3 , 2) is mid-point of Q (-5 , 4) and R (-1 , 0)
a/3 = (-5 + (-1))/2 = -6/2 = -3
a = -9
Suppose A is an invertible n×n matrix and v is an eigenvector of A with associated eigenvalue 4. Convince yourself that v is an eigenvector of the following matrices, and find the associated eigenvalues:
A4, eigenvalue = ?
A−1, eigenvalue = ?
A+4In, eigenvalue = ?
2A, eigenvalue = ?
Answers
The eigenvector of matrix A4 is 4096.
The eigenvalue of the matrix A-1 is 1/8.
(A+4I) has an eigenvalue of 12.
40 is the eigenvalue of 5Av.
The collection of scalar values known as the eigenvalues of a matrix are connected to the set of linear equations that are most likely contained within the matrix equations.
The eigenvectors are also known as the characteristic roots.
If the matrix A's eigen vector v is linked to an eigen value.
Av then equals lamda v.
The fact that v is an eigen vector of A with the value eight is assumed.
hence, Av = 8v.
We must determine the eigenvalue of A4.
A4*v equals A3(8v) = 84*v equals 4096v.
As a result, the eigenvalue of A4 is 4096.
Suppose A has an eigenvalue of 8. The eigenvalue of A-1 is thus 1/8.
It is calculated that the eigenvalue of (A+4I) is (A +4In)v = Av + 4v = 8v + 4v =12v.
(A+4I) has an eigenvalue of 12.
The value of 5Av's eigenvalue is 5Av = 5*8v = 40v.
40 is the eigenvalue of 5Av.
Learn more about the eigen vectors here:
https://brainly.com/question/15423383
#SPJ4
7Use the compound interest formulas Aand A = Pert to solve. Find the accumulatedvalue of an investment of $4000 at 11% compounded continuously for 5 years.= Pp(1+.)"nO $6,915.66O $6,933.01O $6,928.99O $6,832.58

Answers
Given:
Value of an investment of $4000 at 11% compounded continuously for 5 years.
Required:
Find the accumulated value of an investment.
Explanation:
We know that
\(A=Pe^{rt}\)Where, P = Original principal sum
r = Nominal annual interest rate
t = length of time the interest is applied.
Now,
\(\begin{gathered} A=4000\times e^{(0.11\times5)} \\ A=6933.01 \end{gathered}\)Answer:
Hence, option b is correct.
2. Find the distance between point A and point B.
5 units
6 units
7 units
8 units

Answers
You’d count each line going up until you reach the other dot. Or take the number the dot is on and subtract it to the other dots position.
A shopping mall has $20,000 to spend on new tiles for the floor. If each tile costs $2, how many tiles can the mall buy
Answers
oopss wrong one my bad
Hi, can someone please answer this question? Thanks!!!

Answers
Answer:
m∠QPR = 20°
Step-by-step explanation:
Step 1: Find x
4x + 27 + 9x - 115 = 107
13x - 88 = 107
13x = 195
x = 15
Step 2: Find m∠QPR
9(15) - 115
135 - 115
m∠QPR = 20°
A triangular parcel of land has side lengths of 100, 580, and 600 feet. Approximate the area of the land. Round your answer to the nearest foot.
Answers
Answer:
28800 square feet
Step-by-step explanation:
We solve this using the Heron's formula
Area of a Triangle = √s(s - a)(s - b)(s - c)
s = a + b + c/2
s = 100 + 580 + 600/2 = 640
Area of the land(Triangle) = √640 × (640 - 100)(640 - 580)(640 - 600)
= √640 × (540) ×( 60) × (40)
= √(829440000)
= 28800 square feet
Therefore, the approximate the area of the land is 28800 square feet.
Last month Maria hiked a total of 90 miles on two trails: a 5-mile mountain trail and a 10-mile canal trail. Let x represent the number of times Maria hiked the mountain trail, and let y represent the number of times Maria hiked the canal trail.
Answers
Given condition will be represented by linear equation 5x+10y=90.
What is linear equation?
A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation. The standard form of a linear equation in one variable is of the form Ax + B = 0. Here, x is a variable, A is a coefficient and B is constant. The standard form of a linear equation in two variables is of the form Ax + By = C. Here, x and y are variables, A and B are coefficients and C is a constant.
Now,
Total trail hiked=90miles
mountain trail=5mile
canal-trail=10mile
x represent the number of times Maria hiked the mountain trail, and y represent the number of times Maria hiked the canal trail
Therefore,
Linear equation will be 5x+10y=90
To know more about linear equations visit the link
https://brainly.com/question/29739212?referrer=searchResults
#SPJ1
Will give brainliest. Explain in detail, please and thank you.
You went to lunch with your friend, and the bill was $19.00. Your lunch is $3.00 more than your friend's. How much was your friend's lunch?
f+ 3 = 19; $8.00
3f + 2 = 19; $8.00
2 + 3 = 19; $8.00
2 - 3 = 19; $8.00
Answers
Step-by-step explanation:
f, your friends lunch
f + 3, your lunch
f + f + 3 = 19
2f + 3 = 19
2f = 16
f = 8
Your friends lunch was $8
I hope this helped!!!!
Find the equation of the tangent(s) to the curve at the given point. Then graph the curve and tangent(s)
x = 6 sin(t), y = t² + t ; (0,0)
Answers
plot the equations x = 6sin(t), y = t² + t, and y = (1/6)x. The curve and tangent will intersect at the point (0,0).
The equation of the tangent to the curve at the point (0,0) can be found by taking the derivative of y with respect to x:
dy/dx = (dy/dt)/(dx/dt)
dy/dx = (2t + 1)/(6cos(t))
When t = 0, dy/dx = 1/6. So the equation of the tangent is y = (1/6)x.
To graph the curve and tangent, we can use a parametric plotter or a graphing calculator. The curve is a sinusoidal shape, with the highest point at (6,1) and the lowest point at (-6,-1). The tangent at (0,0) is a straight line with a slope of 1/6, passing through the origin.
To find the equation of the tangent(s) to the curve at the given point (0,0), we first need to calculate the derivatives dx/dt and dy/dt. Given x = 6sin(t) and y = t² + t, the derivatives are:
dx/dt = 6cos(t)
dy/dt = 2t + 1
Now, find the slope of the tangent(s) by calculating dy/dx:
dy/dx = (dy/dt) / (dx/dt) = (2t + 1) / (6cos(t))
At the given point (0,0), t = 0. So, substitute t = 0 to find the slope:
dy/dx = (2(0) + 1) / (6cos(0)) = 1 / 6
Since the slope is 1/6, the equation of the tangent is y = (1/6)x.
To graph the curve and tangent, plot the equations x = 6sin(t), y = t² + t, and y = (1/6)x. The curve and tangent will intersect at the point (0,0).
To know more about tangent visit:
https://brainly.com/question/10053881
#SPJ11
Which lines are parallel? Justify your answer.
Lines a and b are parallel because their corresponding angles are congruent.
Lines a and b are parallel because their same side exterior angles are congruent.
Lines e and f are parallel because their corresponding angles are congruent.
Lines e and f are parallel because their same side exterior angles are supplementary.

Answers
Answer:
lines a and b are parallel because their corresponding angles are congruent.
Step-by-step explanation:
Since there are two angles equal to 110 in the same position, lines a and b are parallel because their corresponding angles are congruent.
Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) 5x2 + 2x − 5/x3 − x dx
Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.)
3x2 − 20x + 33/
(2x + 1)(x − 2)2
dx
Answers
The solution to the integral is:
∫ (5x^2 + 2x - 5) / (x^3 - x) dx = 4 ln |x| + ln |x-1| - 5 ln |x+1| + C
The solution to the integral is:
∫ (3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2] dx = (1/3) ln |2x + 1| - (64/25) ln |x - 2| - (49/100)/(x - 2) + C
Evaluating an integralFrom the question, we are to evaluate the given integral.
To evaluate the integral ∫ (5x^2 + 2x - 5) / (x^3 - x) dx, we can use partial fraction decomposition.
First, we factor the denominator:
x^3 - x = x(x^2 - 1) = x(x-1)(x+1)
So, we can write:
(5x^2 + 2x - 5) / (x^3 - x) = A/x + B/(x-1) + C/(x+1)
where A, B, and C are constants to be determined.
Multiplying both sides by the denominator (x^3 - x), we get:
5x^2 + 2x - 5 = A(x-1)(x+1) + B(x)(x+1) + C(x)(x-1)
Substituting x = 0, we get:
-5 = -A - B - C
Substituting x = 1, we get:
2 = 2B
So, B = 1.
Substituting x = -1, we get:
-8 = -2A
So, A = 4
Substituting these values back into the equation above and simplifying, we get:
(5x^2 + 2x - 5) / (x^3 - x) = 4/x + 1/(x-1) - 5/(x+1)
Hence, the integral becomes:
∫ [(5x^2 + 2x - 5) / (x^3 - x)] dx = 4 ln |x| + ln |x-1| - 5 ln |x+1| + C
where C is the constant of integration.
To evaluate the integral ∫ (3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2] dx
First, we factor the denominator:
(2x + 1)(x - 2)^2 = (2x + 1)(x - 2)(x - 2)
So, we can write:
(3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2] = A/(2x + 1) + B/(x - 2) + C/(x - 2)^2
Where A, B, and C are constants to be determined.
Multiplying both sides by the denominator (2x + 1)(x - 2)^2, we get:
3x^2 - 20x + 33 = A(x - 2)^2 + B(2x + 1)(x - 2) + C(2x + 1)
Substituting x = -1/2, we get:
49/4 = 25C
So, C = 49/100.
Substituting x = 2, we get:
3 = 9A
So, A = 1/3.
Substituting these values back into the equation above and simplifying, we get:
(3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2] = 1/(3(2x + 1)) + B/(x - 2) + (49/100)/(x - 2)^2
To find B, we can take the derivative of both sides with respect to x:
d/dx [(3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2]] = d/dx [1/(3(2x + 1)) + B/(x - 2) + (49/100)/(x - 2)^2]
Simplifying and evaluating at x = 2, we get:
-16/25 = -B/4
So, B = 64/25.
Substituting these values back into the equation above and simplifying, we get:
(3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2] = 1/(3(2x + 1)) + (64/25)/(x - 2) + (49/100)/(x - 2)^2
Hence, the integral becomes:
∫ [(3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2]] dx = ∫ [1/(3(2x + 1)) + (64/25)/(x - 2) + (49/100)/(x - 2)^2] dx
= (1/3) ln |2x + 1| - (64/25) ln |x - 2| - (49/100)/(x - 2) + C
Where C is the constant of integration
Learn more on Evaluating integrals here: https://brainly.com/question/28157330
#SPJ1
post office has two counters where customers can buy stamps, etc. if you are interested in the number of customers in the two queues that will form for the counters, what would you take as sample spac
Answers
If we are interested in the number of customers in the two queues that will form for the counters, we would take all the ordered pairs in the form of (x,y) as sample space.
The suitable sample space for the number of customers in the two queues formed in the post office should be the set of all possible combinations of the number of customers in each queue formed. This can be represented in the form of a set of ordered pairs, in which the first element of the ordered pair would represent the number of customers in the first queue and the second element of the same ordered pair would represent the number of customers in the second queue.
For example, if we consider a maximum of 15 customers in the first queue and a maximum of 20 customers in the second queue, the sample space would consist of all the ordered pairs in the form of (x,y),
where x will represent the possible number of customers in the first queue ranging from 0 to 15
and y will represent the possible number of customers in the second queue ranging from 0 to 20.
Learn more about Sample Spaces on
https://brainly.com/question/30206035?referrer=searchResults
#SPJ4
Equation:
a) Show if det(A) = 0, then the graph of the equation is a
line
b) Show if det(A) =/=0, then the graph of the equation is two
intersecting lines
Answers
a). The equation will have only one solution, resulting in a line.
b). The equation will have two distinct solutions, leading to the graph displaying two intersecting lines.
We need to consider the equation in the form of a matrix. Let's say we have a matrix A.
a) If det(A) = 0, it means that the determinant of matrix A is equal to zero. In this case, the graph of the equation represented by matrix A will be a line.
This is because a determinant of zero indicates that the matrix is singular, meaning it does not have an inverse. Consequently, the equation will have only one solution, resulting in a line.
b) On the other hand, if det(A) ≠ 0, it means that the determinant of matrix A is not equal to zero. In this scenario, the graph of the equation represented by matrix A will consist of two intersecting lines.
This is because a non-zero determinant signifies that the matrix is nonsingular, implying that it has an inverse. As a result, the equation will have two distinct solutions, leading to the graph displaying two intersecting lines.
To know more about matrix, visit:
https://brainly.com/question/28180105
#SPJ11
15*\sqrt(72) (15 times root 72. I can't seem to enter a square root symbol)
Answers
Answer:
Step-by-step explanation:ok so if you want too do the the root symbl on what
Thank you so very much for helping

Answers
Answer:
Angle 2
Step-by-step explanation:
They are 90 degrees when added together
Answer:
<2
Step-by-step explanation:
Complementary angles add to 90 degrees ( form right angles)
<1 and <2 add to 90 degrees so they are complementary angles
Evaluate the expression for b = 3 and c = 5.
b2c − 11 =
Answers
Answer:
34Step-by-step explanation:
b = 3 and c = 5Substitute and evaluate:
b²c - 11 =3²*5 - 11 = 9*5 - 11 =45 - 11 =34Answer:
\(b = 3 \ \: \: : c = 5 \\ \\ b {}^{2} c - 11 = \\ \\ \\ {3}^{2} \times 5 - 11 = \\ \\ 9 \times 5 - 11 = \\ \\ 45 - 11 = \\ \\ = 34\)
Find the 49th term.
-15, -10, -5, O, 5, ...
49th term = [?]
1st term + common difference(desired term - 1)
Enter
Answers
Answer:
49th term = 225
Step-by-step explanation:
The following sequence: -15, -10, -5, 0, -5... is an example of an arithmetic progression.
An arithmetic progression or AP for short, is a sequence in which the difference between successive terms is constant. This difference is known as the common difference, and can be found by subtracting a term by its preceding term.
The general formula, for the nth term of an arithmetic progression, is thus:
Tn = a + (n - 1)d, where a = first term, and d = common difference.
In the sequence: -15, -10, -5, 0, 5...,
a = -15, and d = -10--15 = 5
T49 = -15 + (49 - 1)5 = 225
∴ 49th term = 225
Someone text me on sc queenalyssa_05 :)
Answers
Answer:
No
Step-by-step explanation:
Answer:
Why... Um... ok
Step-by-step explanation:
Establish a BN structure model with more than 10 nodes, and explain what is the meaning of the structure.
Answers
The BN structure model with more than 10 nodes can be established. The structure refers to the way the variables are related.
A Bayesian Network (BN) is a probabilistic graphical model that illustrates a set of variables and their probabilistic dependencies. A BN structure is made up of nodes and edges. Nodes represent variables, and edges represent the connections between the variables. The BN structure model can be established by using various algorithms, including structure learning and parameter learning.The BN structure with more than 10 nodes is a complex model with numerous variables and their dependencies. The structure's meaning is how the variables are interrelated, allowing us to estimate the probabilities of certain events or scenarios. The nodes in the structure represent various factors that affect the outcome of an event, and the edges between them demonstrate how these factors are related.The BN structure model is used in many fields, including medical diagnosis, fault diagnosis, and decision making.
The Bayesian Network structure model with more than 10 nodes is a powerful tool for analyzing complex systems. It helps to understand the interrelationships between variables and estimate the probabilities of different events or scenarios. This model is useful in various fields and provides insights into many complex phenomena.
To know more about Nodes visit:
brainly.com/question/32227668
#SPJ11
Help needed. please only answer if you know it.

Answers
Answer:
B
Step-by-step explanation:
f(x) = -(x+3)(x+1)
The zeros are -3 and -1 so we can eliminate graph a
It is negative so it points down
This eliminates graphs c and d