Abby drew a scale drawing to represent her living room. The drawing is rectangular. The longer sides measure 40.5 centimeters and the shorter sides measure 34.5 centimeters.
Abby decides she wants the drawing to be smaller. She will reduce it by a scale factor of 13.
What will be the measure of the shorter sides?
Select from the drop-down menu to correctly complete the statement.
The measure of the shorter sides will be
Choose...
cm.
Answers
The measure of the shorter sides is 3.1 cm and 2.6 cm.
ScalingScaling is used to increase or decrease the size of an object or figure by a factor k.
Given a length of 40.5 cm and width of 34.5 cm.
A smaller rectangle is created by reducing the rectangle by a scale factor of 13 hence:
New length = 40.5/13 = 3.1 cm
New width = 34.5/13 = 2.6 cm
The measure of the shorter sides is 3.1 cm and 2.6 cm.
Find out more on scaling at: https://brainly.com/question/810373
Answer:
11.5
Step-by-step explanation:
Glen... even with a tutor you are incorrect. the only options you can pick are:
11.5
13.5
18.75
and 11.5 if correct for k12
Related Questions
If i have 2 lemons and i give 1 away. how many do i have now?
Answers
.....................................
how do you
Evaluate. 6×(11−6)÷2=
Answers
6x(11-6)divided by 2= 15
PLSSS HELPPPP I NEEED THIS

Answers
Answer:
6. Inverse
7. Direct
8.
a. 21
b. '10, '12
c. Inverse
9.
a. 3000
b. 6000
c. Month 9 (January)
Step-by-step explanation:
Janissa bought 50 cupcake cases for baking. She used 2/5 of the cases to bake vanilla cupcakes. She then used 5/6 of the remaining cases to bake chocolate cupcakes. How many cupcake cases does Janissa have left?
Answers
Jessica has 5 cupcake cases left.
First, divide 50 into groups of five. Next, subtract two groups of five from 50. Third, divide the remaining cases into groups of six. Finally, subtract 5 groups of six from the remains from the last subtraction equation.
The number of cupcake cases that Janissa has left will be 5.
What is Algebra?The analysis of mathematical representations is algebra, and the handling of those symbols is logic.
Janissa bought 50 cupcake cases for baking.
She used 2/5 of the cases to bake vanilla cupcakes. Then the number of vanilla cupcakes will be
⇒ 50 x 2 / 5
⇒ 20 vanilla cupcakes
Then the remaining cupcake cases will be
⇒ 50 - 20
⇒ 30 cupcake cases
She then used 5/6 of the remaining cases to bake chocolate cupcakes. Then the number of chocolate cupcakes will be
⇒ 30 x 5 / 6
⇒ 25 chocolate cupcakes
Then the remaining cupcake cases will be
⇒ 30 - 25
⇒ 5 cupcake cases
Then the number of cupcake cases that Janissa has left will be 5.
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ2
Simplify 9 – 3(4x – 18) + 6x
Answers
The expression is simplified to 7(-x + 9)
What are algebraic expressions?
Algebraic expressions are expressions composed of variables, terms, factors, constants and coefficients.
They are also made up of mathematical or arithmetic operations
Given the expression;
9 – 3(4x – 18) + 6x
expand the bracket
9 - 12x + 54 + 6x
collect like terms, we have;
-12x + 5x + 54 + 9
Add or subtract like terms
-7x + 63
Factor out 7
7(-x + 9)
Thus, the expression is simplified to 7(-x + 9)
Learn more about algebraic expressions here:
https://brainly.com/question/4344214
#SPJ1
write the decimal number in standard form. eight hundred three and one hundred thirty-three thousands
Answers
The standard form of the given decimal number is 803,133.
The given decimal number in words is "eight hundred three and one hundred thirty-three thousands". We have to write this decimal number in standard form. So, let's do it below.
The standard form of a decimal number is the way it's written normally, such as 3,040.00 instead of 3.04 × 103. To write the decimal number in standard form, we have to represent it in the form of a sum of its place values, which have a power of ten (10).
Therefore the standard form of the given decimal number is 803,133.
To learn more about standard form of a decimal number visit : https://brainly.com/question/17136267
#SPJ11
Assume that this proportion is true for ALL children (e.g. that this proportion applies to any group of children), and that the remainder of the questions in this section apply to selections from the population of ALL children. b) If 8 children are chosen, the probability that exactly 4 would draw the nickel too small is: c) If 8 children are chosen at random, the probability that at least one would draw the nickel too small is:
Answers
The probability that at least one child would draw the nickel too small is: P(X ≥ 1) = 1 - P(X = 0).
b) To find the probability that exactly 4 children would draw the nickel too small, we can use the binomial probability formula. The formula is: P(X = k) = (nCk) * (p^k) * (q^(n-k)), where n is the number of trials, k is the number of successes, p is the probability of success, and q is the probability of failure.
In this case, n = 8 (as 8 children are chosen), k = 4 (as exactly 4 children drawing the nickel too small), p = 0.15 (as the probability of a child drawing the nickel too small), and q = 1 - p = 1 - 0.15 = 0.85.
So, the probability that exactly 4 children would draw the nickel too small is: P(X = 4) = (8C4) * (0.15^4) * (0.85^(8-4)).
c) To find the probability that at least one child would draw the nickel too small, we can use the complement rule. The probability of at least one success is equal to 1 minus the probability of no success.
The probability of no success (all children drawing the nickel of the right size) is given by: P(X = 0) = (8C0) * (0.15^0) * (0.85^8).
Therefore, the probability that at least one child would draw the nickel too small is: P(X ≥ 1) = 1 - P(X = 0).
to learn more about probability.
https://brainly.com/question/31828911
#SPJ11
A photographer charges
$
45.50
per hour. How much does the photographer charge for
5
hours of work?
Answers
Answer:
$227.50
Step-by-step explanation:
45.50*5=227.50
Answer:
45.50 times 5=227.5
Step-by-step explanation:
A Speedboat increases in speed uniformly from 20m/s to 30m/s for 12.2 s. What is the acceleration of the speedboat?
Answers
Answer:
0.82 m/s^2
Step-by-step explanation:
Given data
initial velocity=20m/s
Final velocity= 30m/s
Time = 12.2s
Applying the formula
a= v-u/t
a= 30-20/12.2
a= 10/12.2
a= 0.819
a=0.82 m/s^2
i need help please hurry.

Answers
The equation of height of each pyramid inside the cube is,
⇒ h = 2V / B
The equation that represent the volume of each pyramid is,
⇒ V = LWH / 3
The equation that represent the volume of each pyramid if the height of each pyramid is h and area of the base is B,
⇒ V = 1/3 (B × h)
Given that;
To find the formula for height and volume of pyramid.
Now, We know that;
The equation of height of each pyramid inside the cube is,
⇒ h = 2V / B
And, The equation that represent the volume of each pyramid is,
⇒ V = LWH / 3
And, The equation that represent the volume of each pyramid if the height of each pyramid is h and area of the base is B,
⇒ V = 1/3 (B × h)
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
Line r passes through the points (1,1) and (8,9) . line s is perpendicular to r what is the slope of line s?
Answers
Answer: \(\frac{-7}{8}\)
Step-by-step explanation:
First, we will need to find the slope of line r.
\(\displaystyle \frac{y_{2} -y_{1} }{x_{2} -x_{1}} =\frac{9-1}{8-1}=\frac{8}{7}\)
Next, we know that perpendicular slopes are negative reciprocals of one another. To find the slope of line s, we will find the negative reciprocal of line r's slope.
\(\displaystyle \frac{8}{7} \rightarrow \frac{-7}{8}\)
Can someone help me solve this please?
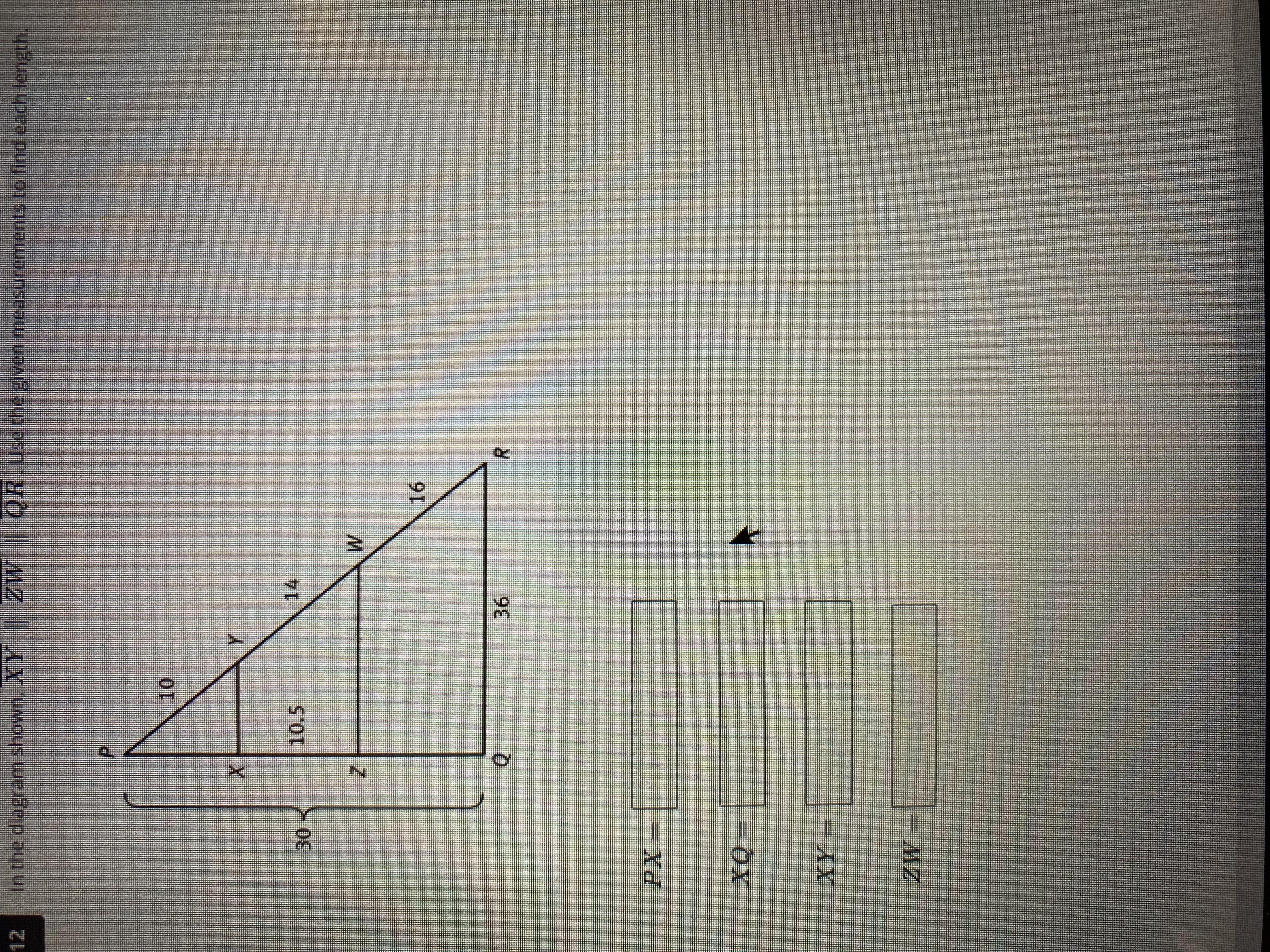
Answers
The segment lengths for this triangle are given as follows:
PX = 7.5.XQ = 22.5.XY = 9.ZW = 21.6. What are similar triangles?Similar triangles are triangles that share these two features given as follows:
Congruent angle measures.Proportional side lengths.There are three triangles in this problem, all of which are similar.
PQR.PZW.PXY.The length of segment PX can be obtained with triangles PQR and PXY, as follows:
PX/30 = 10/40
PX/30 = 1/4
4PX = 30
PX = 7.5.
The length of segment XQ is found applying the segment addition postulate, as follows:
PQ + XQ = 30
7.5 + XQ = 30
XQ = 22.5.
The length of segment XY can also be obtained with the similarity of triangles PXY and PQR, as follows:
XY/36 = 10/40
XY/36 = 1/4
4XY = 36
XY = 9.
The length of segment ZW is obtained with the similarity of triangles PZW and PQR, as follows:
ZW/36 = 24/40
ZW/36 = 0.6.
ZW = 36 x 0.6
ZW = 21.6.
More can be learned about similar triangles at brainly.com/question/14285697
#SPJ1
Which of the following is a true statement? a) -11 >-8 b) -11 < -8 c) -11 = -8 d) -11 = -8
Answers
The true statement is b) -11 < -8. This means that -11 is less than -8, and the value of -11 is smaller. When comparing negative numbers, the larger the absolute value, the smaller the number itself.
These symbols are used to indicate the relationship between two numbers and are denoted by >, <, and =, respectively.
In conclusion, understanding the concepts of greater than, less than, and equal to is an important part of mathematics and is useful in many real-world situations. By knowing the true statement, you can make accurate comparisons and solve problems more effectively.
to know more about true statement refer here
https://brainly.com/question/10705953#
#SPJ11
jeans bedroom is 14 feet by 12 feet, the cost for carpet is $29.65 per square yard. this includes installation
Answers
Answer:
Roughly $553.57
Step-by-step explanation:
14ft*12ft = 168 square ft
168 square ft*(1/9) ~ 18.67 square yd
18.67*$29.65 ~ $553.57
Which of the following lists of ordered Pairs is a function?

Answers
Answer: B
Step-by-step explanation:
trust me the answer is B if the answer is not reported me
What is the inverse

Answers
Answer:this is the answer

Answer:
\(f^{-1}(x)=3x-6\)
Step-by-step explanation:
Let's replace \(f(x)\) with \(x\) and replace \(x\) with \(f^{-1}(x)\) ad solve.
\(x=1/3*f^{-1}(x)+2\)
\(x-2=1/3*f^{-1}(x)\)
\(f^{-1}(x)=3(x-2)\).
\(\boxed{f^{-1}(x)=3x-6}\)
: A study found that the mean waiting time to see a physician at an outpatient clinic was 40 minutes with a standard deviation of 28 minutes. Use Excel to find the probability in each case. (Round your answers to 4 decimal places. ) More than an hour's wait Less than 20 minutes At least 10 minutes
Answers
The standard deviation of wait time is 13.8564.
The length of time patients must wait to see a doctor in a local clinic is uniformly distributed between 25 minutes and 73 minutes. We have to find the standard deviation of the wait time.
The square root of the variance of a random variable, sample, statistical population, data collection, or probability distribution is its standard deviation.
The standard deviation in statistics is a measure of the degree of variation or dispersion in a set of values.
A low standard deviation implies that the values are close to the set's mean, whereas a high standard deviation shows that the values are spread out over a larger range.
S² = (73 - 25)²/12
S² = (48)²/12
S² = 192
S = √192
S = 13.8564
Hence, The standard deviation of wait time is 13.8564.
To learn more about standard deviation, visit :
brainly.com/question/13905583
#SPJ4
complete question:
the length of time patients must wait to see a doctor in a local clinic is uniformly distributed between 25 minutes and 73 minutes. what is the standard deviation of wait time? group of answer choices
at a sale, costs were sold for $10 each. if the coats originally cost $20 each, what percentage of its original price was a coat sold for?
Answers
How many lines of symmetry does a hexagon have that will reflect it onto itself?
Answers
A regular hexagon has six lines of symmetry to map onto itself using reflections.
The number of lines of symmetry a hexagon have that will reflect it onto itself is 6.
The given shape is hexagon.
A line of symmetry is the line that divides a shape or an object into two equal and symmetrical parts.
A hexagon has six lines of symmetry. Each line of symmetry is a line that divides the hexagon into two equal halves that are reflections of one another. When all six lines of symmetry are present, the hexagon can be reflected over itself.
Therefore, the number of lines of symmetry a hexagon have that will reflect it onto itself is 6.
Learn more about line of symmetry here:
https://brainly.com/question/30963765.
#SPJ6
3 ft, 4 ft, 6 ft 1 5 in, 12 in, 13 in 25 cm, 31 cm, 40 cm
Which one in would make a right angle in a triangle
Answers
Answer: . . . . . . Step-by-step explanation:
Two lines are intersecting. What is the value of x? Enter your answer in the box.
(x + 23)
(2x + 4)°
Answers
Answer:
x = 19
Step-by-step explanation:
To find the value of x, you set the equations as equal to each other:
\(x+23 = 2x+4\)
Then you simplify:
\(23 = 2x + 4 - x\\23 = x + 4\\23-4 = x\\19=x\)
how many ways are there to choose a half dozen donuts from 10 varieties a) if there are no two donuts of the same variety. so you need to select 6 varieties without replacement from 10 varieties: c(10,6) b) if there are at least two varieties.
Answers
a) There are 210 ways no two donuts of the same variety; and
b) There are 10⁶ ways at least two varieties.
a) If there are no two donuts of the same variety:Suppose that there are 10 varieties of donuts. You have to select half a dozen or 6 varieties from these 10 varieties without repetition. This means that you cannot choose the same variety twice.
There are a total of 10 varieties to choose from. Therefore, the number of ways you can choose 6 varieties is given by the combination of 10 choose 6. This is represented as:
\($$\begin{aligned}\text{Combination of 10 choose 6}&=\frac{10!}{(10-6)!6!} \\ &=\frac{10 \times 9 \times 8 \times 7 \times 6 \times 5}{4 \times 3 \times 2 \times 1 \times 6 \times 5} \\ &=210\end{aligned}$$\)
Therefore, there are 210 ways to choose half a dozen donuts if there are no two donuts of the same variety.
b) If there are at least two varietiesSuppose that there are 10 varieties of donuts. You have to select half a dozen or 6 varieties from these 10 varieties with repetition. This means that you can choose the same variety twice, thrice, or more.
There are 10 varieties to choose from. Therefore, the number of ways you can choose half a dozen donuts is given by 10⁶ = 1,000,000 ways.
Therefore, there are 1,000,000 ways to choose half a dozen donuts if there are at least two varieties.
To know more about the "combination": https://brainly.com/question/4658834
#SPJ11
A shoemaker sold a pair of for $245.99 if the buyer a $300.00 bill, how much will the buyer receive in change?
*two decimal places don't forget your $ sign. Example: $50.00 NOT 50*
Answers
Answer:
$54.01
Step-by-step explanation:
All you have to do is $300.00-$245.99 .
Find the matrix P that orthogonally diagonalizes A. Compute P-¹ AP. A = [3 2 4]
[2 0 2]
[4 2 3]
Answers
To orthogonally diagonalize matrix A, we need to find a diagonal matrix D and an orthogonal matrix P such that A = PDP^T, where D contains the eigenvalues of A and P contains the corresponding eigenvectors. the final result is:
P^-1AP = [(2√6)/3 0 0]
[0 0 0]
[0 0 -2√6/3]
Let's go through the steps to find P and D:
Step 1: Find the eigenvalues λ of matrix A by solving the characteristic equation |A - λI| = 0.
|3-λ 2 4|
| 2 -λ 2| = (3-λ)(-λ)(3-λ) + 2(2)(2-λ) - 4(2-λ) = 0
|4 2 3-λ|
Simplifying the determinant equation, we get:
(λ-1)(λ-6)(λ+1) = 0
Solving the equation, we find three eigenvalues: λ1 = 1, λ2 = 6, λ3 = -1.
Step 2: For each eigenvalue, find the corresponding eigenvector.
For λ1 = 1:
(A - λ1I)X = 0
|2 2 4| |x1| |0|
|2 -1 2| |x2| = |0|
|4 2 2| |x3| |0|
Solving this system of equations, we find the eigenvector X1 = (1, -2, 1).
Similarly, for λ2 = 6, we find X2 = (2, 1, 2), and for λ3 = -1, we find X3 = (2, -1, 2).
Step 3: Normalize the eigenvectors to make them unit vectors.
Normalizing X1, X2, and X3, we get:
X1' = (1/√6)(1, -2, 1)
X2' = (1/3)(2, 1, 2)
X3' = (1/3)(2, -1, 2)
Step 4: Construct the orthogonal matrix P using the normalized eigenvectors.
P = [X1' X2' X3']
= [(1/√6) (1/3) (1/3)
(-2/√6) (1/3) (-1/3)
(1/√6) (2/3) (2/3)]
Step 5: Construct the diagonal matrix D using the eigenvalues.
D = [λ1 0 0
0 λ2 0
0 0 λ3]
= [1 0 0
0 6 0
0 0 -1]
Finally, we can compute P^-1AP:
P^-1AP = [(1/√6) (-2/√6) (1/√6)]
[(1/3) (1/3) (-1/3)]
[(1/3) (2/3) (2/3)]
* [3 2 4]
[2 0 2]
[4 2 3]
* [(1/√6) (-2/√6) (1/√6)]
[(1/3) (1/3) (-1/3)]
[(1/3) (2/3) (2/3)]
Multiplying these matrices, we get:
P^-1AP = [(2√6)/3 0 0]
[0 0 0]
[0 0 -2√6/3]
Therefore, the final result is:
P^-1AP = [(2√6)/3 0 0]
[0 0 0]
[0 0 -2√6/3]
To know more about orthogonally diagonalize, click here: brainly.com/question/31970381
#SPJ11
Si una llave entrega 32 litros en 5 minutos . cuantos tardara dicha llave en llenar 288 litros? porfa es urgente:c
Answers
The time required to fill 288 liters of water would be 288/6.4 = 45 minutes.Therefore, the time taken by the key to fill 288 liters of water is 45 minutes.
The given data in the problem is that a key delivers 32 liters of water in 5 minutes. We are required to calculate how much time it will take to fill 288 liters of water.So, let's proceed with the solution,Step 1: We need to find out how many liters of water is filled in one minute. We can use the unitary method to solve the problem. We know that 32 liters of water is filled in 5 minutes. Hence, in one minute, the amount of water filled would be32/5 = 6.4 litersStep 2: Now, we need to find the time required to fill 288 liters of water. Again, we can use the unitary method. We have found out that the amount of water filled in one minute is 6.4 liters. Therefore, the time required to fill 288 liters of water would be 288/6.4 = 45 minutes.Therefore, the time taken by the key to fill 288 liters of water is 45 minutes.
Learn more about time :
https://brainly.com/question/28050940
#SPJ11
x² - y² Let f(x, y) = x Y 0 Which of the following is/are correct? P. The domain of f(x,y) is R2 Q. lim f(x, y) exists. (x,y) →(0,0) R. f(x,y) is continuous at (0, 0). OQ and R OP, Q. and R OP only OP and Q Q only (x, y) = (0,0) (x, y) = (0,0)
Answers
all three statements P, Q, and R are correct.
To determine whether statements P, Q, and R are correct, we'll examine each one separately:
P: The domain of f(x, y) is R²
To find the domain of f(x, y), we need to identify any restrictions on x and y. In this case, we see that the function is undefined when x = y because it results in division by zero. Thus, the domain of f(x, y) is all points in R² except (0, 0). Therefore, statement P is correct.
Q: lim(x, y)→(0,0) f(x, y) exists
To determine if the limit exists as (x, y) approaches (0, 0), we need to evaluate the function along different paths and check if the limit is the same regardless of the path chosen.
Let's consider the limit along the path y = x:
lim(x, y)→(0,0) f(x, y) = lim(x, x)→(0,0) (x² - x²)/(x - x) = lim(x, x)→(0,0) 0/0
Here, we encounter an indeterminate form of 0/0, indicating that further evaluation is needed. By simplifying the expression, we get:
lim(x, y)→(0,0) f(x, y) = lim(x, x)→(0,0) 0 = 0
The limit is equal to 0, regardless of the chosen path. Hence, the limit exists as (x, y) approaches (0, 0). Therefore, statement Q is correct.
R: f(x, y) is continuous at (0, 0)
For a function to be continuous at a point, the following conditions need to be satisfied:
1. The function must be defined at that point (0, 0) - which it is.
2. The limit of the function as (x, y) approaches (0, 0) must exist - we established in statement Q that the limit is 0.
Both conditions are met, indicating that f(x, y) is continuous at (0, 0). Therefore, statement R is correct.
In summary, all three statements P, Q, and R are correct.
Learn more about limit here
https://brainly.com/question/32513969
#SPJ4
Complete question is below
Let f(x, y) = { (x² - y²)/(x-y) (x,y)≠(0,0)
= { 0 , (x, y) = (0, 0)
Which of the following is/are correct?
P The domain of f(x,y) is R²
Q lim(x, y)→(0,0) f(x, y) exists
R f(x,y) is continuous at (0,0)
the z value for a 97.8% confidence interval estimation is
Answers
The z value for a 97.8% confidence interval estimation is determined as 2.29.
What is the z value for a 97.8% confidence?The z value for a 97.8% confidence interval estimation is calculated as follows;
The find the Z score, go to a Z lookup table which is found in a textbook or on an internet source. z table is created to give the possibility in a one-tailed analysis.
A confidence interval is a two-tailed examination, in order to prepare the z score for 97.8%, look up the probability of 98.9%.
The value of 98.9% is
= (0.978 + 1 )/ 2
= 0.989 or 98.9%.
This implies that the z score of the date is 2.29.
Learn more about z-score here: https://brainly.com/question/28000192
#SPJ1
suppose a research firm conducted a survey to determine the mean amount steady smokers spend on cigarettes during a week. a sample of 140 steady smokers revealed that the population mean is $20. the population standard deviation is $7. what is the probability that a sample of 140 steady smokers spend between $19 and $21? rev: 05 09 2022 qc cs-304733 multiple choice 0.4545 0.0455 0.9090 1.0000
Answers
To find the probability that a sample of 140 steady smokers spend between $19 and $21, we can use the standard normal distribution.
First, we need to calculate the standard error of the mean (SEM) using the formula SEM = \(σ / √n\), where σ is the population standard deviation and n is the sample size. In this case, \(σ\)= $7 and n = 140. So, SEM = $7 / \(√140\).
Next, we need to convert the values $19 and $21 to z-scores using the formula z = \((x - μ)\)/ SEM, where x is the value, μ is the population mean, and SEM is the standard error of the mean. For $19, z = ($19 - $20) / SEM, and for $21, z = ($21 - $20) / SEM.
Using z-scores, we can find the probabilities associated with each z-score using a standard normal distribution table or a calculator. In this case, we want to find the probability that z is between the two z-scores.
Finally, we subtract the lower probability from the higher probability to find the probability that a sample of 140 steady smokers spend between $19 and $21.
To know more about deviation visit:
https://brainly.com/question/31835352
#SPJ11
Show that the process X(t):=e t/2
cos(W(t)),0≤t≤T, is a martingale w.r.t. any filtration for Brownian motion and represent it as an Itô process on any time interval [0,T],T>0.
Answers
A stochastic process X(t) is called a martingale if the expected value of X(t) given all information available up to and including time s is equal to the value of X(s).
Thus, to show that the process X(t):=e^(t/2)cos(W(t)), 0 ≤ t ≤ T is a martingale w.r.t. any filtration for Brownian motion, we need to prove that E(X(t)|F_s) = X(s), where F_s is the sigma-algebra of all events up to time s.
As X(t) is of the form e^(t/2)cos(W(t)), we can use Itô's lemma to obtain the differential form:dX = e^(t/2)cos(W(t))dW - 1/2 e^(t/2)sin(W(t))dt
Taking the expectation on both sides of this equation gives:E(dX) = E(e^(t/2)cos(W(t))dW) - 1/2 E(e^(t/2)sin(W(t))dt)Now, as E(dW) = 0 and E(dW^2) = dt, the first term of the right-hand side vanishes.
For the second term, we can use the fact that sin(W(t)) is independent of F_s and therefore can be taken outside the conditional expectation:
E(dX) = - 1/2 E(e^(t/2)sin(W(t)))dt = 0Since dX is zero-mean, it follows that X(t) is a martingale w.r.t. any filtration for Brownian motion.
Now, let's represent X(t) as an Itô process on the interval [0,T]. Applying Itô's lemma to X(t) gives:
dX = e^(t/2)cos(W(t))dW - 1/2 e^(t/2)sin(W(t))dt= dM + 1/2 e^(t/2)sin(W(t))dt
where M is a martingale with M(0) = 0.
Thus, X(t) can be represented as an Itô process on [0,T] of the form:
X(t) = M(t) + ∫₀ᵗ 1/2 e^(s/2)sin(W(s))ds
Hence, we have shown that X(t) is a martingale w.r.t. any filtration for Brownian motion and represented it as an Itô process on any time interval [0,T], T > 0.
To know more about martingale visit:
brainly.com/question/32735198
#SPJ11
What are the first four terms of a sequence where he rule is 7(n+2)?
Answers
Answer:
Step-by-step explanation:
for n=1 it is 7(1+2)=21
for n=2 it is 7(2+2)=28
for n=3 it is 7(3+2)=35