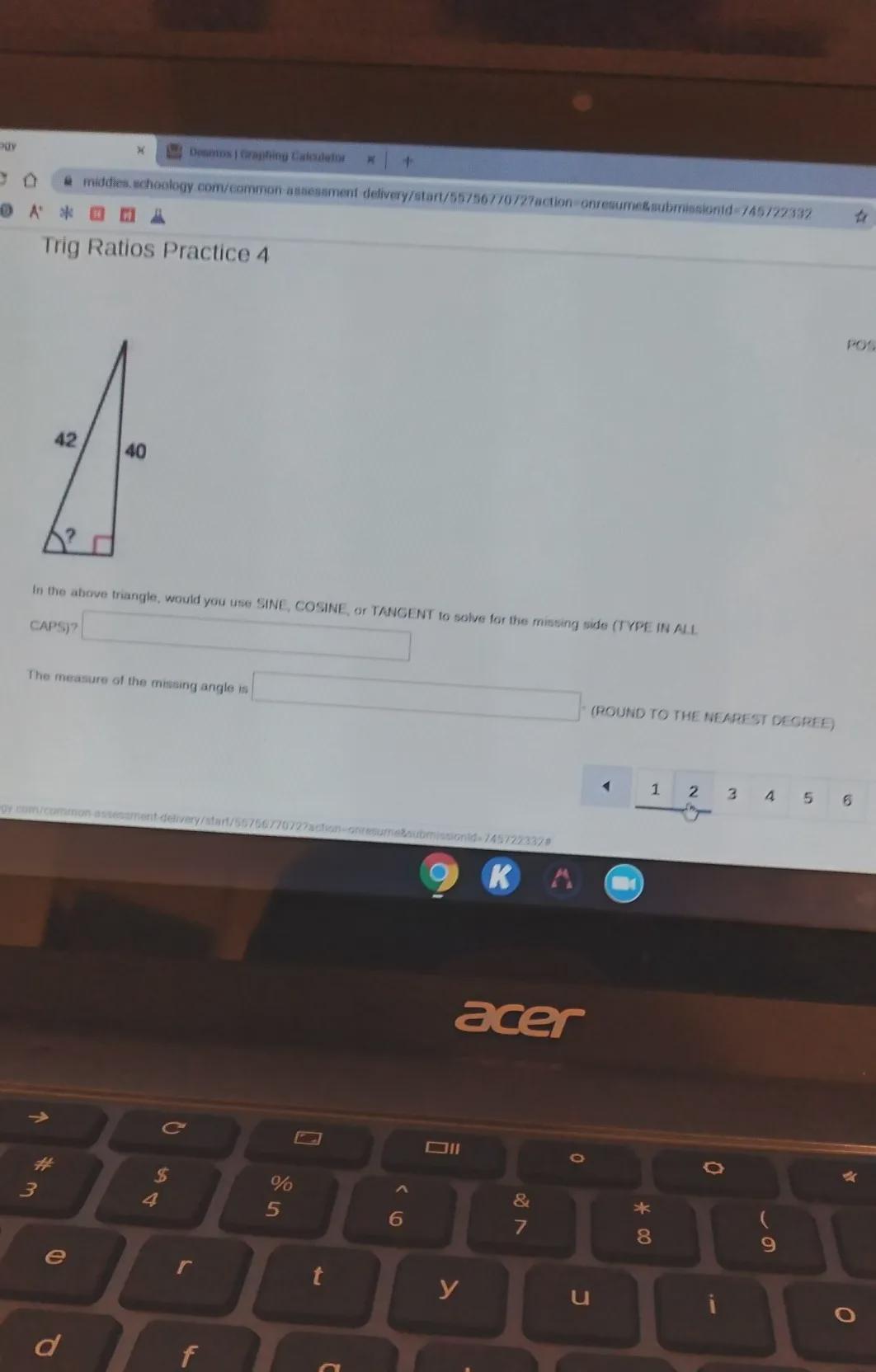
• A* * * * X Trig Ratios Practice 4 POSSIBLE POINT 42 40 In the above triangle, would you use SINE, COSINE, or TANGENT to solve for the missing side (TYPE IN ALL CAPS)? The measure of the missing angle is (ROUND TO THE NEAREST DEGREE). 1 2 3 4 5 6 7 8

x = (12 ± √(-16)) / 4,The solutions would be complex numbers.

To solve quadratic equations of the form ax2 + bx + c = 0, use the quadratic formula. For this situation, your condition is as of now as a quadratic condition, with a = 2, b = - 12, and c = 20.

The quadratic formula is:

x = (-b ± √\((b^2 - 4ac)\)) / 2a

Plugging in the values for a, b, and c, we get:

x = (-(-12) ± √\(((-12)^2 - 4(2)(20)))\) / 2(2)

Simplifying the expression inside the square root:

x = (12 ± √\((144 - 160)\)) / 4

x = (12 ± √(-16)) / 4

Since the square foundation of a negative number is definitely not a genuine number, this condition has no genuine arrangements. Complex numbers would provide the answers.

know more about complex number visit :

https://brainly.com/question/20566728

#SPJ1

The tangent at any point of a circle is perpendicular to the radius through the point of contact by showing that line PQ coincides with the radius OP.

Let us assume that we have a circle with center O and radius r.

Let P be any point on the circle .

And let Q be the point of intersection of the tangent to the circle at P and the radius OP,

To prove that PQ is perpendicular to OP.

First, we observe that OP is a radius of the circle and therefore its length is r.

Since PQ is tangent to the circle at point P,

It is perpendicular to the radius drawn from the center of the circle to point P.

As the tangent to a circle is perpendicular to the radius drawn to the point of contact.

This implies, angle QOP is a right angle.

Next, triangle OPQ is a right triangle with right angle at Q.

By the Pythagorean Theorem, we have,

OP²= OQ² + PQ²

Substituting r for OP and noting that OQ = r since Q is on the radius. we have,

⇒ r² = r²+ PQ²

Subtracting r² from both sides, we get,

⇒ PQ² = 0

This implies that PQ = 0,

In other words, that point Q coincides with point P.

PQ is a line that coincides with the radius OP.

And since angle QOP is a right angle, we can conclude that PQ is perpendicular to OP.

Therefore, it is proved that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

learn more about tangent here

brainly.com/question/270661

#SPJ1

The above question is incomplete, the complete question is:

Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

For the given graph related to savings on y-axis and time on x-axis, the constant of proportionality is equal to 4, and the equation representing the relationship between the savings and the time is given by y = 4x.

As given in the question,

From the graph,

y-axis represents the savings in dollars

x-axis represents the time in seconds

Let us consider savings represents by y and time represents by x.

Form the graph we can see that,

When x = 10 ⇒ y = 40

when x = 15 ⇒ y = 60

Graph represents the straight line so it is linear function.

y = 40

⇒ y= 4(10)

⇒ y= 4x

⇒y ∝ x

⇒Constant of proportionality 'k' = 4

Now, for the equation consider two coordinates on the graph,

(x₁ , y₁) = (10, 40)

(x₂ , y₂) = (15, 60)

( y-y₁)/ (x-x₁) = (y₂ -y₁) / (x₂ - x₁)

⇒( y- 40)/(x-10) = (60 -40)/ (15-10)

⇒ y-40 = 4(x-10)

⇒y = 4x

Therefore, for the given graph related to savings on y-axis and time on x-axis, the constant of proportionality is equal to 4, and the equation representing the relationship between the savings and the time is given by y = 4x.

Learn more about proportionality here

brainly.com/question/22620356

#SPJ1

Answer:(a) The rate of decay is 14.4% per day, which can be written as a decimal by dividing by 100: r = 0.144.

(b) The formula for continuous decay is given by:

A = A₀ * e^(-rt)

where A is the remaining amount of the substance after time t, A₀ is the initial amount, r is the rate of decay, and e is the mathematical constant approximately equal to 2.71828.

Plugging in the given values, we get:

A = 140 * e^(-0.144*15)

A = 140 * e^(-2.16)

A ≈ 47.23

Therefore, after 15 days, approximately 47.23 mg of the radioactive substance will be left, rounded to two decimal places.

Step-by-step explanation:

The perimeter of the circular figure is P = 36.85 feet

A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “center”. Every line that passes through the circle forms the line of reflection symmetry. Also, the circle has rotational symmetry around the center for every angle

The circumference of circle = 2πr

The area of the circle = πr²

where r is the radius of the circle

The standard form of a circle is

( x - h )² + ( y - k )² = r²,

where r is the radius of the circle and (h,k) is the center of the circle.

Given data ,

Let the perimeter of the figure be represented as P

Now , the perimeter of the figure P = perimeter of circle + perimeter of lengths of sides

The total lengths of sides = ( 3 + 3 + 3 + 3 + 3 + 3 ) feet

The total lengths of sides = 18 feet

And , the circumference of circle = 2πr

The diameter of the circle d = 12 feet - 6 feet

The diameter of the circle d = 6 feet

So , the radius of the circle r = d/2 = 3 feet

And , the circumference of circle = 2 x π x 3

The circumference of circle = 6π

So , perimeter of the figure P = ( 6π + 18 ) feet

Perimeter of the figure P = 36.849 feet

Hence , the perimeter of the figure is 36.85 feet

To learn more about circle click :

https://brainly.com/question/28391204

#SPJ1

The value of y is 48.

To find the value of y in this scenario, we need to use the fact that the angle bisector of ∠JSL splits it into two congruent angles.

Let's denote one of these congruent angles as ∠HSL and the other as ∠LSJ. Since ∠JSL is bisected, we have:

m∠JSL = m∠HSL + m∠LSJ

Given that m∠JSL = (4y - 10)° and m∠HSL = m∠LSJ = ∠HSJ = (y + 43)°, we can substitute these values into the equation:

4y - 10 = (y + 43) + (y + 43)

Simplifying the equation:

4y - 10 = 2y + 86

Subtracting 2y from both sides:

2y - 10 = 86

Adding 10 to both sides:

2y = 96

Dividing both sides by 2:

y = 48

Therefore, the value of y is 48.

For more questions on value of y

https://brainly.com/question/28896476

#SPJ8

Answer: T'=(-1,-1), U'=(-3,-1), V'=(-1,-4)

Step-by-step explanation:

Answer:

\(\boxed {\boxed {\sf A.\ r=0.17454}}\)

Step-by-step explanation:

The correlation coefficient helps us understand the relationship between variables.

A positive correlation is a positive number. A negative correlation is a negative number.

We can automatically eliminate choices B and D because they are negative, but we are looking for a positive correlation.

A number closer to 1 indicates a strong correlation. If the number is closer to 0, it's weak.

The two choices left are:

C is very close to 1, so it's a strong correlation.

We want to find the weak one, which must be A because it is closer to 0.

Answer:

a) 2. 4pi (in) , 4pi  

  3. 8pi , 16pi

  4. 16pi, 64pi

  5. 32 pi  ,  256pi

Step-by-step explanation:

b) when radius increase , the areas and circumferences increase to

circumference = 2 pi * radius ; so if you double the radius , circumference will be double

area = pi * radius * radius ; if you double the radius , area will be 2^2 or 4 times

c) circumference will be triple and

area will be 3^2 or 9 times

Area=l×w

Function:-

\(\\ \sf\longmapsto (l*w)(x)\)

\(\\ \sf\longmapsto l(x)*w(x)\)

\(\\ \sf\longmapsto (x+24)(x+16)\)

\(\\ \sf\longmapsto x^2+40x+384\)

Answer:

Step-by-step explanation:

81: 360*100 =

(81*100): 360 =

8100: 360 = 22.5

By analyzing the graph and evaluating the objective function at each vertex of the feasible region, we can find the optimal solution, which is the vertex that maximizes the objective function z = 3x + y.

To find the optimal solution of the given problem using the graphical method, we need to plot the feasible region determined by the given constraints and then identify the point within that region that maximizes the objective function.

Let's start by graphing the constraints:

1. Plot the line 2x - y = 5. To do this, find two points on the line by setting x = 0 and solving for y, and setting y = 0 and solving for x. Connect the two points to draw the line.

2. Plot the line -x + 3y = 6 using a similar process.

3. The x-axis and y-axis represent the constraints x ≥ 0 and y ≥ 0, respectively.

Next, identify the feasible region, which is the region where all the constraints are satisfied. This region will be the intersection of the shaded regions determined by each constraint.

Finally, we need to identify the point within the feasible region that maximizes the objective function z = 3x + y. The optimal solution will be the vertex of the feasible region that gives the highest value for the objective function. This can be determined by evaluating the objective function at each vertex and comparing the values.

Note: Without a specific graph or additional information, it is not possible to provide the precise coordinates of the optimal solution in this case.

For more such questions on graph

https://brainly.com/question/19040584

#SPJ8

Answer:

\(a_{n}\) = 8\(a_{n-1}\) ; a₁ = - 2

Step-by-step explanation:

a recursive formula in a geometric sequence allows a term to be found by multiplying the preceding term by the common ratio r

here r = \(\frac{a_{2} }{a_{1} }\) = \(\frac{-16}{-2}\) = 8 , then

\(a_{n}\) = 8\(a_{n-1}\) ; a₁ = - 2

9514 1404 393

Answer:

  m∠QPR = 94°

Step-by-step explanation:

Given:

  m∠QPS = 180°

  m∠QPR = 7x -4°

  m∠RPS = 9x -40°

Find:

  m∠QPR

Solution:

  m∠QPR + m∠QPR = 180°

  (7x -4°) +(9x -40°) = 180°

  16x = 224° . . . . . . . . . . . . . add 44°

  x = 14° . . . . . . . . . . . . . divide by 16

  m∠QPR = 7x -4° = 7(14°) -4°

  m∠QPR = 94°

Answer:

The equation of this line is y = -4.

Answer:

y=-4

Step-by-step explanation:

zero slope m=0

y-y1=m(x-x1)

y-(-4)=0(x-(-9))

y+4=0

y=-4

2z ÷ [z – (z – 4)]

Sub z=8 into the expression

2(8) ÷ [8 – (8 – 4)] = 16 ÷ 4

                             = 4

Answer: gurl you think i know

Step-by-step explanation:

The angle between the two forces of 560 N and 222 N is 80.96°

The resultant of two vectors P and Q refer to the magnitudes of the vectors and it can be expressed by the formula \(\mathbf{R = \sqrt{P^2 +Q^2 +2PQ cos \theta }}\)

Now, using the above equation, we can easily determine the angle between the forces of the two vectors as follows:

\(\mathbf{634 = \sqrt{560^2 +222^2 + 2(560 \times 222) \ Cos \theta }}\)

\(\mathbf{401956 =313600 +49284 + 248640 \ Cos \theta }}\)

\(\mathbf{401956 -313600 -49284 = 248640 \ Cos \theta }}\)

\(\mathbf{39072= 248640 \ Cos \theta }}\)

\(\mathbf{ Cos \theta = \dfrac{39072}{248640}}}\)

\(\mathbf{Cos \theta =0.1571}\)

\(\mathbf{ \theta =80.96^0}\)

Therefore, we can conclude that the angle between the forces is 80.96°

Learn more about the resultant of two vectors here:

https://brainly.com/question/19802988

Answer:

20+2=22

Step-by-step explanation:

When you go down by 2, then use the Inverse Operation to add it up.

The length of the tile Candace is designing is 3 /2 meters.

The rectangular tiles he is designing has the following dimension:

width = 3/5 meters

area = 9/10 meters

The length of the tiles Candace is designing can be calculated below:

area of a rectangle = lw

where

l = length

w  = width

Therefore,

9/10 = 3/5 l

cross multiply

9 × 5 = 3 × 10l

45 = 30l

divide both sides by 30

45 / 30 = l

l = 9 / 6 = 3 / 2 meters

length = 3 / 2 meters

learn more: https://brainly.com/question/23272398?referrer=searchResults

The truck driver would deliver 105 packages in a 7 hours day

An equation is an expression that shows how numbers and variables are related to each other using mathematical operators.

Let y represent the number of packages delivered by the truck driver in x hours. Using the point (1, 15) and (4, 60). Hence, the equation is:

y - 15 = [(60-15)/(4-1)](x - 1)

y = 15x

For a 7 hour day (x = 7):

y = 15(7) = 105

The driver would deliver 105 packages in 7 hours

Find out more on equation at: https://brainly.com/question/29174899

#SPJ1

Answer:

2520

Step-by-step explanation:

There are 7 letters in MCHNLRN and they can be arranged into 7 ways:

7! = 5040 ways in total

However, the letter 'N' is repeated so we have to divide it by 2.

5040 ÷ 2 = 2520 ways

Answer:

2,520 ways

Step-by-step explanation:

MCHNLRN has 7 letters with one repetition.

therefore, =7!/2!

=2,520 ways

Step-by-step explanation:

Team A time is    1 garden / ( 1 garden/ 2 hr + 1 garden/4 hr) = 1 1/3 hr

Team B =   1 / ( 1/3 + 1/3) =  1 1/2 hr

Team A wins !

"The correct answer is option A." The missing coordinates of point Q are (a, c/2).We are given the coordinates of points P and N as (0, c) and (2a, 0), respectively. We are also given that point Q lies on the same line as points P, Q, and N. We need to find the missing coordinates of point Q.

Since point Q lies on the same line as P, Q, and N, its x-coordinate must be halfway between the x-coordinates of points P and N. That is, the x-coordinate of Q is:

x-coordinate of Q = (x-coordinate of P + x-coordinate of N) / 2

x-coordinate of Q = (0 + 2a) / 2 = a

So, we know that the x-coordinate of point Q is a.

To find the y-coordinate of point Q, we can use the fact that point Q lies on the same line as point P, which has coordinates (0, c). The equation of the line passing through P and N is:

y - c = (0 - c) / (2a - 0) * (x - 0)

Simplifying this equation gives:

y - c = -c/2a * xy = -c/2a * x + c

Substituting x = a in this equation gives:

y = -c/2a * a + cy = -c/2 + cy = c/2

So, we know that the y-coordinate of point Q is c/2.

For such more questions on missing coordinates:

https://brainly.com/question/27481419

#SPJ11

Answer:

1

Hope this helps sorry I'm not really good at explaining math, cause when I do nobody understands.

On solving the provided question, we can say that -  95 confidence interval Z alpha 2 = 1.96, CI = (4.1 , 53.9)

The z critical value is 1.96 for a test with a 95% confidence level (e.g. = 0.05). The z critical value is 5.576 for a test with a 99% confidence level (for instance, with = 0.01).

The two red tails represent the alpha level split by two. Finding the z-score for an alpha level for a two-tailed test is what is meant when a question asks you to determine z alpha/2. The confidence interval may be subtracted from 100% to calculate alpha, which is connected to confidence levels.

for 95% confidence,

\(Z_{\frac{\alpha }{2} }\) = 1.96

CI = (5279 - 5250) ± 1.96\(\sqrt{\frac{140^2}{395} + \frac{210^2}{395} } \\\)

CI = (4.1 , 53.9)

To know more about Z alpha 2 visit:

https://brainly.com/question/19168390

#SPJ4

The solutions to the equation \($x^2 = 6 - x$\) are \($x = -3$\) and \(x = 2$.\)

What is square of a number?

The square of a number is the result of multiplying the number by itself. In mathematical notation, the square of a number "\(x\)" is written as "\(x^2\)".

Let's call the number we are looking for "x".

According to the problem statement, we have:

\($$x^2 = 6 - x$$\)

We can rearrange this equation to get:

\($$x^2 + x - 6 = 0$$\)

Now, we can factor the left-hand side of this equation:

\($$(x + 3)(x - 2) = 0$$\)

So, either \($x + 3 = 0$\) or \(x - 2 = 0$.\) Solving for x in each case gives us:

\($$x = -3 \text{ or } x = 2$$\)

Therefore, the solutions to the equation \($x^2 = 6 - x$\) are \($x = -3$\) and \(x = 2$.\)

To learn more about square of a number visit:

https://brainly.com/question/27307830

#SPJ1

Complete Question

A milling process has an upper specification of 1.68 millimeters and a lower specification of 1.52 millimeters. A sample of parts had a mean of 1.6 millimeters with a standard deviation of 0.03 millimeters. what standard deviation will be needed to achieve a process capability index f 2.0?

Answer:

The value required is  \(\sigma = 0.0133\)

Step-by-step explanation:

From the question we are told that

   The upper specification is  \(USL = 1.68 \ mm\)

    The lower specification is  \(LSL = 1.52 \ mm\)

     The sample mean is  \(\mu = 1.6 \ mm\)

     The standard deviation is  \(\sigma = 0.03 \ mm\)

Generally the capability index in mathematically represented as

             \(Cpk = min[ \frac{USL - \mu }{ 3 * \sigma } , \frac{\mu - LSL }{ 3 * \sigma } ]\)

Now what min means is that the value of  CPk is the minimum between the value is the bracket

          substituting value given in the question

           \(Cpk = min[ \frac{1.68 - 1.6 }{ 3 * 0.03 } , \frac{1.60 - 1.52 }{ 3 * 0.03} ]\)

=>      \(Cpk = min[ 0.88 , 0.88 ]\)

So

         \(Cpk = 0.88\)

Now from the question we are asked to evaluated the value of  standard deviation that will produce a  capability index of 2

Now let assuming that

         \(\frac{\mu - LSL }{ 3 * \sigma } = 2\)

So

         \(\frac{ 1.60 - 1.52 }{ 3 * \sigma } = 2\)

=>    \(0.08 = 6 \sigma\)

=>     \(\sigma = 0.0133\)

So

        \(\frac{ 1.68 - 1.60 }{ 3 * 0.0133 }\)

=>      \(2\)

Hence

      \(Cpk = min[ 2, 2 ]\)

So

    \(Cpk = 2\)

So    \(\sigma = 0.0133\) is  the value of standard deviation required