A wheel with a 50 cm radius is rotating at a rate of 5 radians/sec. What is the linear speed of a point on its rim in meters per minute?
Answers
The linear speed of the wheel is 150 m/min
The given parameters;
radius of the wheel, r = 50 cm = 0.5 m
angular speed, ω = 5 rad/s
The linear speed of the wheel in meter per second is calculated as follows;
\(v = \omega r\)
where;
v is the linear speed of the wheel
Substitute the given values and solve for v;
v = 0.5 x 5
v = 2.5 m/s
The linear speed in meter per minutes is calculated as;
\(v = 2.5 \frac{m}{s} \times \frac{60 \ s}{ 1 \min} = 150 \ m/min\)
Thus, the linear speed of the wheel is 150 m/min
Learn more here: https://brainly.com/question/16645415
Related Questions
A school keeps track of the percentage of scholars who pack lunch versus buy lunch. On Monday, 80% of scholars packed lunch. On Tuesday, 70% of the scholars who packed lunch do so again, and 50% of those who bought lunch on Monday pack lunch on Tuesday. Assume all scholars either pack lunch or buy lunch. Find the percent change in the number of scholars who bought lunch from Monday to Tuesday, and indicate whether this was an increase or decrease.
Answers
Answer:
Increase by 10% of students that bought lunch.
Step-by-step explanation:
I think the percent change was by 10%. Because 10% of those students who packed lunched on Monday did not pack lunch on Tuesday, and assuming that they either buy or pack it that means that 10% more students bought lunch.
The Fahrenheit temperature readings on 66 Spring mornings in New York City are
summarized in the table below. Construct and label a frequency histogram of the data
with an appropriate scale.
Temp (°F) Number of Days.
30-39
2
40-49
26
50-59
28
60-69
8
70-79
2
Graph answer Click and drag to make a rectangle. Click a rectangle to delete it.
Answers
To construct a frequency histogram based on the given temperature data, we will use the temperature ranges as the x-axis and the number of days as the y-axis.
The temperature ranges and their corresponding frequencies are as follows:
30-39: 2 days
40-49: 26 days
50-59: 28 days
60-69: 8 days
70-79: 2 days
To create the histogram, we will represent each temperature range as a bar and the height of each bar will correspond to the frequency of days.
Using an appropriate scale, we can label the x-axis with the temperature ranges (30-39, 40-49, 50-59, 60-69, 70-79) and the y-axis with the frequency values.
Now, we can draw rectangles (bars) on the graph, with the base of each rectangle corresponding to the temperature range and the height representing the frequency of days. The height of each bar will be determined by the corresponding frequency value.
For such more question on frequency
https://brainly.com/question/254161
#SPJ8
Harper is starting a printing business. She purchases plain t-shirts for $5 dollars each and spends $150 for printing equipment She decides to sell printed shirts for $10 each. How many t-shirts does Harper need to sell so that the amount of money she spends to start her business and the amount of money she earns are the same.
Answers
Answer:
30
Step-by-step explanation:
150/5 = 30
30+30+30+30+30 = 150
Ty received 3/5 of his CDs as gifts. If he has 60 CDs, how many were gifts?
Answers
Answer:
36 CDs were gifts-------------------
3/5 part of 60 CD's were gifts.
That makes:
3/5 * 60 = 180/5 = 36 CDsplease tell me how this done with steps so I can do this on my own as well

Answers
Answer:
6
Step-by-step explanation:
Because J is the midpoint of KL, it means that KJ ans JL are equal.
Think about it like this:
What is the midpoint (or halfway point) of 4 and 8? The answer is 6, you would do 4 + 8 which is 12 and divide it by 2. There is an equal distance of 2 between 4 and the midpoint, and midpoint and 8. In the same way, JL is also 6Hope this helps!
Step-by-step explanation:
the midpoint of a line splits the line into 2 equally long parts.
therefore, JI must be equally long to KJ.
x = 6
and with KJ = 6 and JI = 6, then KI = KJ + JI = 6+6 = 12
Write the equation of the line in fully simplified slope-intercept form.

Answers
The equation of the line in fully simplified slope-intercept form is y = 1/2x + 4
How to determine the equation of the lineFrom the question, we have the following parameters that can be used in our computation:
The graph
On the graph, we have the following points
(0, 4) and (-8, 0)
A linear equation is represented as
y = mx + c
Using the point (0, 4), we have
4 = 0 * m + c
So, we have
c = 4
Using the point (-8, 0), we have
0 = -8 * m + 4
So, we have
m = 1/2
So, we have
m = 1/2 and c = 4
Recall that we have
y = mx + c
This gives
y = 1/2x + 4
Hence, the equation is y = 1/2x + 4
Read more about linear equation at
https://brainly.com/question/14323743
#SPJ1
Two trains leave stations 416 miles apart at the same time and travel toward each other. One train travels at 85 miles per hour while the other travels at 75 miles per hour. How long will it take for the two trains to meet?
Answers
About 5 hours it will take
Answer:
2.6 hours
Step-by-step explanation:
75+85
160x/160= 416/160
=2.6
Which data set contains an outlier?
A. {15, 15, 15, 16, 16, 17, 18}
B. {45, 46, 47, 47, 49, 49}
C. {9, 10, 10, 11.4, 12.1, 12.6}
D. {16, 42, 45, 45, 46, 48}
Answers
The data set which contains an outlier from the given answer choices is; Choice D; {16, 42, 45, 45, 46, 48}.
What is an outlier?An outlier in a set of data values is a data value which differs significantly from other data points and hence, tends to affect the mean of such set of data values significantly.
On this note, choice D is the set of data values which contains an outlier.
Read more on outliers;
https://brainly.com/question/2749543
#SPJ1
Can someone please help me (giving brainliest to whoever is right)
Answers
use prime factorization for 600
Answers
Answer: 2^3 x 3 x 5^2
Step-by-step explanation:
All we have to do is divide 600
alright
Chopping off the two zeros:
6x100
Factoring 6:
2x3x100
Factoring 100:
2x3x10x10:
Factoring both 10s:
2x3x2x5x2x5
2^3 x 3 x 5^2
Therefore, we have factored 600 into 2^3 x 3 x 5^2
Twelve of the last 16 winners of the school science fair have been seventh grade students. Mona placed 3 red marbles and 1 green marble in a bag to create a simulation to predict whether future science fair winners will be seventh graders. According to Mona’s model, what is the probability that the next 4 winners will all be seventh grade students?
Answers
Answer:
what is the determinant of human value
-5/8 - (-4/3)
Pls help

Answers
Answer:
Step 1 of 2: Subtract.
Subtract
(
negative 5 over 8
−
5
8
) − (
negative 4 over 3
−
4
3
) =
17 over 24
17
24
Step 1 of 2: Subtract, sub-step a: Subtract a negative.
Subtract a negative
negative 5 over 8
−
5
8
− (
negative 4 over 3
−
4
3
) =
negative 5 over 8
−
5
8
+
4 over 3
4
3
Subtracting a negative is the same as adding a positive.
Step 1 of 2: Subtract, sub-step b: Find common denominator.
Find common denominator
negative 5 over 8
−
5
8
+
4 over 3
4
3
= −
( 5 × 3 ) over ( 8 × 3 )
5 × 3
8 × 3
+
( 4 × 8 ) over ( 3 × 8 )
4 × 8
3 × 8
=
negative 15 over 24
−
15
24
+
32 over 24
32
24
24 is the least common multiple of denominators 8 and 3. Use it to convert to equivalent fractions with this common denominator.
Step 1 of 2: Subtract, sub-step c: Add.
Add
negative 15 over 24
−
15
24
+
32 over 24
32
24
=
(
negative 15
−15 + 32 ) over 24
negative 15
−15 + 32
24
=
17 over 24
17
24
Answer:
The answer would be 17/24
Step-by-step explanation:
1. Common denominator is going to be 24. 3(-5/8) - 8(-4/3)
2. Next multiply. -15/24 + 32/24
3. After addition you get 17/24 or 0.7
Mr guny deposits $45900 in a savings account that pays 1.5% interest compounded quarterly. find the first quarter's interest find the first quarter's balance
Answers
If we use m compounded per year Bt will be to:
\(\begin{gathered} B_t=B_0(1+\frac{r}{m})^{mt} \\ I_t=B_t-B_0 \end{gathered}\)Where:
B0 = deposits = $45900
r = compound yearly interest rate = 1.5% = 0.015
t = years
m = 4
The first quarter's interest
We have following:
\(\begin{gathered} B_t=45900\cdot(1+\frac{0.015}{4})^{4\cdot\frac{3}{12}} \\ B_t=45900\cdot(1+\frac{0.015}{4})^1 \\ B_t=46072.13 \end{gathered}\)Then:
\(I_{1th\text{ quarter}}=46072.125-45900=172.13\)Answer: The interest in first quarter is $172.13
The first quarter's balance
The balance is Bt, therefore:
Answer: The balance after first quarter is $46,072.13
What is the measure of angle B?

Answers
Answer:
58 degrees
Step-by-step explanation:
find x first
8x+2 + 6x + 80 = 180
14x + 82 = 180
14x = 98
x = 7
then substitute it back into the angle measure of B
angle b = 8x + 2
8(7) + 2 = 58
The slope of a line is ¾. A different line passes through the points (6, 3) & (-1, 5). Are the lines parallel? Why or why not?

Answers
Answer:
B. They are not parallel because their slopes are not equal.
Step-by-step explanation:
Find the slope of the line that runs through points (6, 3) and (-1, 5):
\( slope (m) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{5 - 3}{-1 - 6} \)
\( slope (m) = \frac{2}{-7} = -\frac{2}{7} \)
Since the slope of the line that passes through points (6, 3) and (-1, 5) is not the same with line that has a slope of ¾, therefore, both lines cannot be parallel.
The answer is "B. They are not parallel because their slopes are not equal."
The formula V equals 1.225 √a is used to estimate how far a person can see on a clear day,where V is the visibility in miles and A is the altitude in feet. What is Ty's visibility if out the upper window of a building with a altitude of 1,602 feet? Round your answer to the nearest whole number.
Answers
Ty's visibility if out the upper window of a building with an altitude of 1,602 feet is 49.
What is altitude?
The height of an object in relation to a planet's or a natural satellite's surface, like sea level or land. the degree to which a celestial body is elevated above the horizon.
Here, we have
Given
The formula V = 1.225 √a is used to estimate how far a person can see on a clear day, where V is the visibility in miles and A is the altitude in feet.
We have to find Ty's visibility out the upper window of a building with an altitude of 1,602 feet.
We know that
V = 1.225 √a
a = 1,602 feet.
V = 1.225 √1602
V = 49
Hence, Ty's visibility out the upper window of a building with an altitude of 1,602 feet is 49.
To learn more about the altitude from the given link
https://brainly.com/question/28786198
#SPJ1
I need help with this question please!! See attached
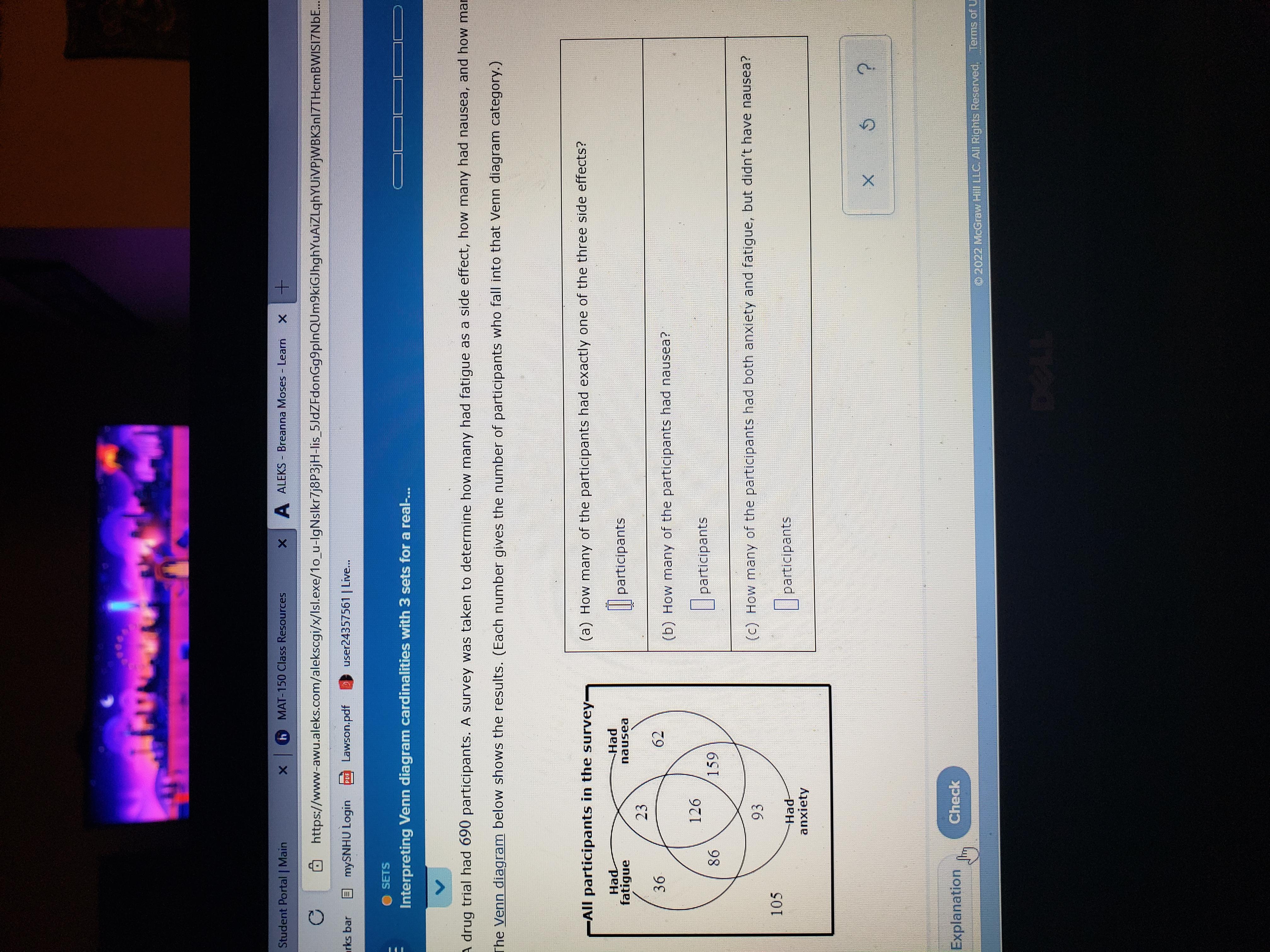
Answers
Answer:
(a) 191 had side effects
(b) 370 had nausea
(c) 86 had both anxiety and fatigue
Step-by-step explanation:
See attached. We look at the Venn diagram to answer the different questions.
If you are color blind let me know and I will mark the attachment more clearly.

A golf analyst claims that the standard deviation of the 18-hole scores for a golfer is stokes. State and in words and in symbols. Then determine whether the hypothesis test for this claim is left-tailed, right-tailed, or two-tailed. Explain your reasoning.
Answers
Answer:
Left tailed.
Step-by-step explanation:
A claim (alternative hypothesis) is set against the null hypothesis.
The claim (alternative hypothesis) of the golf analyst is that the standard deviation of the 18-hole scores for a golfer is less than 2.1 strokes
Ha: Sd< 2.1
The null hypothesis will be opposite of the alternate hypothesis
H0: sd ≥ 2.1
A test for which the entire rejection region is located in only one of the two tails - either left or right- is called one tailed test.
In the given example the acceptance region is located in the area greater or equal to 2.1 . The rejection region lies to the left and the acceptance region lies to the right.
As the rejection region lies to the left, it is a left tailed test.
Also if the alternative hypothesis contains equality less than it is left tailed.
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
4 ^-3 rewrite without an exponent
Answers
Answer:
(1/4)³
Step-by-step explanation:
Hope it helps you
Answer:
\(\frac{1}{64}\)
Step-by-step explanation:
Negative exponents means you bring the base to the denominator, which becomes a fraction.
\(4^{-3} \\=\frac{1}{4^{3}}\)
The question wants us to write without an exponent.
The \(4^{3} = 4 * 4* 4=64\)
So, it becomes:
\(\frac{1}{64}\)
A square garden has a length of (x+3) ft and a width of (x+2) ft. what is the perimeter and area of the garden?
Answers
Answer:
Perimeter:\(4x+10\) feet
Area:\(x^{2}+5x+6\) feet
Step-by-step explanation:
The perimeter is equal to 2*width +2*length. The width is x+2 and the length is x+3, therefore the perimeter is equal to 2x+4+2x+6 which equals 4x+10.
The area is equal to width*length
(x+3)(x+2)=\(x^{2}+2x+3x+6=x^{2}+5x+6\)
The diagram shows a scale drawing of the
side elevation of a building.
3 cm represents 1 m.
What is the width of the building in metres?
(Give your answer in meters).
Please answer, and no spam.

Answers
Answer:
The answer for the width of the building 5m
Step-by-step Explanation:
3cm=1m
15cm=x
cross multiply
x×3=15×1
3x=15
divide both sides by 3
3x/3=15/3x=5m
Write the following expression using the fewest possible terms. the expression quantity three fourths times t minus 5 plus two fifths times t end quantity minus quantity five eighths times t plus 17 end quantity
Answers
The required result if the given expression is \(11[\frac{t}{40}-2]\).
What is expression?
A finite combination of symbols that are well-formed in accordance with context-dependent principles constitutes an expression or mathematical expression.
Given the expression quantity three fourths times t minus 5 plus two fifths times t end quantity minus quantity five eighths times t plus 17 end quantity.
We write it in expression and we get
\(\frac{3}{4} \times t-5+\frac{2}{5} \times t-\frac{5}{8} \times t +17\)
Now
\(\frac{3}{4} \times t-5+\frac{2}{5} \times t-[\frac{5}{8} \times t +17]\\=\frac{3t}{4} +\frac{2t}{5} -\frac{5t}{8} -22\\=\frac{2t}{5}+\frac{6t-5t}{8}-22\\=\frac{2t}{5}+\frac{t}{8}-22\\=\frac{16t-5t}{40}-22\\=\frac{11t}{40}-22\\=11[\frac{t}{40}-2]\)
Therefore, the required result if the given expression is \(11[\frac{t}{40}-2]\).
To learn more about expression from the given link
https://brainly.com/question/723406
#SPJ1
don't use the answer above this one, its wrong.
y=2x + 4
-7x + 6y=14 substitution
Answers
Answer:
Below
Step-by-step explanation:
y=2x + 4
-7x + 6y=14 Sub in the value of y given in the first equation
-7x + 6 ( 2x+4) = 14
-7x + 12x + 24 = 14
5x = -10
x = -2 use this value in one of the equations to calculate y= 0
Use any of the methods to determine whether the series converges or diverges. Give reasons for your answer.
∑[infinity]n=17n2−4n+3
12+2n6
Answers
Answer:
It means \(\sum_{n=1}^\inf} = \frac{7n^2-4n+3}{12+2n^6}\) also converges.
Step-by-step explanation:
The actual Series is::
\(\sum_{n=1}^\inf} = \frac{7n^2-4n+3}{12+2n^6}\)
The method we are going to use is comparison method:
According to comparison method, we have:
\(\sum_{n=1}^{inf}a_n\ \ \ \ \ \ \ \ \sum_{n=1}^{inf}b_n\)
If series one converges, the second converges and if second diverges series, one diverges
Now Simplify the given series:
Taking"n^2"common from numerator and "n^6"from denominator.
\(=\frac{n^2[7-\frac{4}{n}+\frac{3}{n^2}]}{n^6[\frac{12}{n^6}+2]} \\\\=\frac{[7-\frac{4}{n}+\frac{3}{n^2}]}{n^4[\frac{12}{n^6}+2]}\)
\(\sum_{n=1}^{inf}a_n=\sum_{n=1}^{inf}\frac{[7-\frac{4}{n}+\frac{3}{n^2}]}{[\frac{12}{n^6}+2]}\ \ \ \ \ \ \ \ \sum_{n=1}^{inf}b_n=\sum_{n=1}^{inf} \frac{1}{n^4}\)
Now:
\(\sum_{n=1}^{inf}a_n=\sum_{n=1}^{inf}\frac{[7-\frac{4}{n}+\frac{3}{n^2}]}{[\frac{12}{n^6}+2]}\\ \\\lim_{n \to \infty} a_n = \lim_{n \to \infty} \frac{[7-\frac{4}{n}+\frac{3}{n^2}]}{[\frac{12}{n^6}+2]}\\=\frac{7-\frac{4}{inf}+\frac{3}{inf}}{\frac{12}{inf}+2}\\\\=\frac{7}{2}\)
So a_n is finite, so it converges.
Similarly b_n converges according to p-test.
P-test:
General form:
\(\sum_{n=1}^{inf}\frac{1}{n^p}\)
if p>1 then series converges. In oue case we have:
\(\sum_{n=1}^{inf}b_n=\frac{1}{n^4}\)
p=4 >1, so b_n also converges.
According to comparison test if both series converges, the final series also converges.
It means \(\sum_{n=1}^\inf} = \frac{7n^2-4n+3}{12+2n^6}\) also converges.
Solve each system by elimination.2x + 5y = -243x - 5y = 141. Which variable has an opposite pair? Type x or y2. Solve for x .3. Substitute the value x of into one of the original equations to solve for y .4. Write the solution as an ordered pair (x,y)( , )

Answers
The Solution:
Given the pair of equations below:
\(\begin{gathered} 2x+5y=-24 \\ 3x-5y=14 \end{gathered}\)We are asked to solve by the Elimination Method.
1. The variable that has an opposite pair is [variable y]
2. To solve for x, we shall add the corresponding terms in both equations together.
\(\begin{gathered} 2x+5y=-24 \\ +(3x-5y=14) \\ ------------ \\ 5x+0=-10 \\ 5x=-10 \end{gathered}\)Dividing both sides by 5, we get
\(\begin{gathered} \frac{5x}{5}=\frac{-10}{5} \\ \\ x=-2 \end{gathered}\)3. Substituting -2 for x in the first equation, to get the value of y.
\(\begin{gathered} 2x+5y=-24 \\ 2(-2)+5y=-24 \\ -4+5y=-24 \end{gathered}\)Bringing the like terms to one side, we get
\(\begin{gathered} 5y=-24+4 \\ 5y=-20 \end{gathered}\)Dividing both sides by 5, we get
\(\begin{gathered} \frac{5y}{5}=\frac{-20}{5} \\ \\ y=-4 \end{gathered}\)4. Writing the solution as an ordered pair, we have
\((x,y)=(-2,-4)\)Therefore, the correct answer is (-2 , -4)
This month my metro water services bill was $36.34 and my Madison Suburban Utilty District bill was $26.03. My total water bill was $
Answers
Total water bill for the month is $62.37.
It seems that you may have accidentally left out the total amount of your water bill.
The total amount by simply adding the amounts of the individual bills together:
Total water bill =\($36.34 + $26.03\)
= \($62.37\)
You have not provided enough information to determine your total water bill.
You have only given the amounts of your individual bills from Metro Water Services and Madison Suburban Utility District.
To find your total water bill, you simply need to add the two bills together.
So, the total amount you owe for water this month would be:
Total water bill = \($36.34 + $26.03\)
= \($62.37\)
It appears that you may have forgotten to include the full amount of your water bill by accident.
Simple addition of the separate bill amounts yields the following sum:
Water bill total = \($36.34 + $26.03\)
= \($62.37\)
Your total water bill cannot be calculated because not enough information has been given.
Only the amounts of your individual Metro Water Services and Madison Suburban Utility District bills have been provided.
You just need to combine the two invoices together to get your total water bill.
As a result, this month's total water bill for you would be:
Water bill total = \($36.34 + $26.03\)
= \($62.37\)
For similar questions on water bill
https://brainly.com/question/31119915
#SPJ11
Given that the sum of the first n terms of the provided series is 6560 determine the value of n (2,6,18,54....)

Answers
Answer:
n = 8
Step-by-step explanation:
The given sequence, 2, 6, 18, 54. . ., is a geometric sequence.
It has a common ratio of 3 => \( \frac{6}{2} = \frac{18}{6} = \frac{54}{18} = 3 \)
Thus, the sum of the first n terms of a geometric sequence is given as \(S_n = \frac{a_1(1 - r^n)}{1 - r}\)
Where,
\( a_1 \) = first term of the series = 2
r = common ratio = 3
\( S_n \) = sum of the first n terms = 6,560
Plug in the above values into the formula
\(6,560 = \frac{2(1 - 3^n)}{1 - 3}\)
\( 6,560 = \frac{2(1 - 3^n)}{-2} \)
\( 6,560 = \frac{1 - 3^n}{-1} \)
Multiply both sides by -1
\( -6,560 = 1 - 3^n \)
Subtract 1 from both sides
\( -6,560 - 1 = - 3^n \)
\( -6,561 = - 3^n \)
\( 6,561 = 3^n \)
Evaluate
\( 3^8 = 3^n \)
3 cancels 3
\( 8 = n \)
The value of n = 8
<1 and <2 form a linear pair. The measure of <2 is six more than twice the measure of <1. Find the measure of <2
Answers
Answer:
122 Degrees
Step-by-step explanation:
Since we are given that angle 1 and 2 make a linear pair:
angle 1 + angle 2 = 180 degrees ----------------------------(1)
We have also been told that angle 2 is 6 more than twice the measure of angle 1
Which means: angle 2 = (2*angle1) + 6 -------------------(2)
From putting the value of angle 2 in (1) from (2)
angle 1 + 2*angle 1 + 6 = 180
3*angle 1 = 174
angle 1 = 58 degrees -----------------------(3)
From (1) and (3):
angle 2 + 58 = 180
angle 2 = 122 degrees
Therefore, the measure of angle 2 is 122 degrees
Which box-and-whisker plot represents this data: 6,9, 13, 13, 18, 20, 24, 25, 26, 28, 30, 30?
Answers
Check the pictures for the answer



