a truck is traveling at a speed of 42 miles per hour.which function gives the number of miles driven in t hours?

Given:

The figure of circle E. \(m\angle ABD=(11x-3)^\circ,m\angle ACD=(8x+15)^\circ\).

To find:

The measure of arc AD.

Solution:

We know that the inscribed angles on the same arc are congruent and their measures are equal.

\(\angle ABD\) and \(\angle ACD\) are inscribed angles on the same arc AD. So,

\(m\angle ABD=m\angle ACD\)

\(11x-3=8x+15\)

\(11x-8x=3+15\)

\(3x=18\)

\(x=6\)

Now,

\(m\angle ABD=(11x-3)^\circ\)

\(m\angle ABD=(11(6)-3)^\circ\)

\(m\angle ABD=(66-3)^\circ\)

\(m\angle ABD=63^\circ\)

We know that the intercepted arc is always twice of the inscribed angle.

\(m(Arc(AD))=2\times m\angle ABD\)

\(m(Arc(AD))=2\times 63^\circ\)

\(m(Arc(AD))=126^\circ\)

Therefore, the measure of arc AD is 126 degrees.

Answer:

Step-by-step explanation:

28/4 is the radius of the half circle which is 7

if the whole thing was a rectangle the area would be

28 * 24 = 672

area of a half circle is A = pi * r^2/2

pi is also 22/7

A = 22/7 * 7^2/2 -> 22/7 * 49/2 -> 77

2 half circles' area is 77*2 = 154

672 - 154 = 518

The time the airplane will arrive at its destination is; 12:30 pm

The relationship between distance, time and speed is;

Speed = Distance/time

Now, we are given;

Distance = 1375 miles

Speed = 550 miles per hour

Thus;

Time = Distance/Speed

Time taken = 1375/550

Time taken = 2.5 hours

Thus, if he leaves by 10 am, then the time to arrive is;

10 am + 2.5 hours = 12:30 pm

Read more about Distance and Time at;https://brainly.com/question/26046491

#SPJ1

Answer:

A. h = h₀ + u·t - 1/2·g·t²

B. 30.9 m

C. 4.73 seconds

2. A. h = h₀ + u·t - 1/2·a·t²

B. 67.8 m

C. Approximately 25.73 seconds

3. A. h = h₀ + u·t - 1/2·g·t²

B. 31.38 m

C. Approximately 5.142 seconds

D. Approximately 32.9 m

Step-by-step explanation:

The given parameters are;

The initial height of the ball, h₀ = 15 m

The upward velocity with which the ball is thrown, u = 20 m/sec.

The acceleration due to gravity, g = 9.8 m/s²

A. The relation between the height, h, and the time, t, after the ball is released is given as follows;

h = h₀ + u·t - 1/2·g·t²

B. The height of the ball after 3 seconds is given by substitution as follows;

At t = 3 seconds, h = 15 + 20 × 3 - 1/2 × 9.8 × 3² = 30.9

The height of the ball, h, after 3 seconds is h = 30.9 m

C. The time the ball takes to hit the ground = 2 × The time it takes to maximum height + The time it takes the ball to fall with an initial velocity of 20 m/sec for 15 m height

The time it takes to maximum height, \(t_{max}\), is given as follows;

v = u - g·\(t_{max}\)

Where;

v = The final velocity = 0 at maximum height

Therefore, we have;

0 = 20 - 9.8 × \(t_{max}\)

∴ \(t_{max}\) = 20/9.8 ≈ 2.0408

The time it takes to maximum height, \(t_{max}\) ≈ 2.0408 seconds

The time it takes the ball to fall with an initial velocity of 20 m/sec for 15 m height, \(t_{15}\) is  given as follows;

v₂² = u₂² + 2·g·h₀

v₂² = 20² + 2×9.8×15 = 694

v₂ = √694 ≈ 26.344 m/s

v₂ ≈ 26.344 m/s

From, v₂ = u₂ + g·\(t_{15}\), we have;

26.344 = 20 + 9.8×t

9.8·\(t_{15}\) = 26.344 - 20 = 6.344

∴ \(t_{15}\) = 6.344/9.8 ≈ 0.647

The ball will hit the ground after 2 × \(t_{max}\)  + \(t_{15}\) ≈ 2 × 2.0408 + 0.647 ≈ 4.7286

The ball will hit the ground after approximately 4.7286 ≈ 4.73 seconds

2. When the ball is thrown upward from the Moon, we have;

The acceleration due to gravity on the moon, a = 1.6 m/s², therefore, we have;

A. The relation between the height, h, and the time, t, after the ball is released is given as follows;

h = h₀ + u·t - 1/2·a·t²

B. The height of the ball after 3 seconds is given by substitution as follows;

At t = 3 seconds, h = 15 + 20 × 3 - 1/2 × 1.6 × 3² = 67.8

The height of the ball, h,  thrown on the Moon, after 3 seconds is h = 67.8 m

C. The time the ball takes to hit the ground = 2 × The time it takes to maximum height + The time it takes the ball to fall with an initial velocity of 20 m/sec for 15 m height

The time it takes to maximum height, \(t_{max}\), is given as follows;

v = u - a·\(t_{max}\)

Where;

v = The final velocity = 0 at maximum height

Therefore, we have;

0 = 20 - 1.6 × \(t_{max}\)

∴ \(t_{max}\) = 20/1.6 = 12.5

The time it takes to maximum height, \(t_{max}\) = 12.5 seconds

The time it takes the ball to fall with an initial velocity of 20 m/sec for 15 m height, \(t_{15}\) is  given as follows;

v₂² = u₂² + 2·a·h₀

v₂² = 20² + 2×1.6×15 = 448

v₂ = √448 ≈ 21.166 m/s

v₂ ≈ 21.166 m/s

From, v₂ = u₂ + a·\(t_{15}\), we have;

21.166 = 20 + 9.8×t

1.6·\(t_{15}\) = 21.166 - 20 = 1.166

∴ \(t_{15}\) = 1.166/1.6 ≈ 0.72785

The ball will hit the ground after 2 × \(t_{max}\)  + \(t_{15}\) ≈ 2 × 12.5 + 0.72875 = 25.72875 ≈ 27.73

The ball will hit the ground after approximately 25.73 seconds

3. The height from which the ball is kicked, h₀ = 1 m

The initial velocity of the ball, u = 25 m/sec

The acceleration due to gravity, g = 9.8 m/s²

The relationship between the height, h and the time, t after the ball is released, is given as follows;

h = h₀ + u·t - 1/2·g·t²

B. The height of the ball after 2 seconds is given as follows;

At t = 2, h = 1 + 25 × 2 - 1/2 × 9.81 × 2² = 31.38

The height of the ball, after 2 seconds, h = 31.38 m

C. The time it takes the ball to hit the ground is given by the following kinematic equation, as follows;

h = h₀ + u·t - 1/2·g·t²

At the ground level, h = 0, therefore, we have;

0 = 1 + 25·t - 4.9·t²

Therefore, by the quadratic formula, we have;

t =  (-25  ± √(25² - 4×(-4.9)×1))/(2 × -4.9)

Therefore, t ≈ 5.142, or t ≈ -0.03969

Given that the time is a natural number, we have, t ≈ 5.142 seconds

D. The maximum height, \(h_{max}\) the ball reaches is given as follows;

From the kinematic equation, v² = u² - 2·g·h,

Where;

v = 0 at maximum height

h = The height the ball reaches above the initial height, we have;

0² = u² - 2·g·h

u² = 2·g·h

h = u²/(2·g) = 25²/(2 × 9.8) ≈ 31.888

\(h_{max}\) = h₀ + h = 1 + 31.888 ≈ 32.9

The maximum height the ball reaches, \(h_{max}\) ≈ 32.9 m

The hexadecimal number 0x3d is equal to 61 in decimal (base 10).

To convert the hexadecimal number 0x3D to decimal (base 10), we need to understand the positional system of both bases. In hexadecimal, each digit represents a power of 16, starting from the rightmost digit. The digits range from 0 to 9, and then from A to F, where A represents 10 and F represents 15, In hexadecimal (base 16) representation, each digit can have values from 0 to 15. The digits from 0 to 9 represent their respective values, and the letters A to F represent the values 10 to 15.

To convert 0x3d to decimal, we can break down the number as follows:

0x3d = (3 * 16^1) + (13 * 16^0)

Simplifying the expression:

0x3d = (3 * 16) + 13

0x3d = 48 + 13

0x3d = 61

learn more about hexadecimal here:

https://brainly.com/question/28875438

#SPJ11

To describe the transformations performed on f(x) = 3^x to get g(x) = -2(3)^x + 4, we can analyze the changes in the equation.

Reflection over the x-axis:

The negative sign in front of the term 2(3)^x indicates a reflection over the x-axis. This means that the graph of g(x) is a reflection of f(x) about the x-axis.

Stretch by a factor of 2:

The coefficient 2 in front of the term (3)^x represents a vertical stretch. It stretches the graph vertically by a factor of 2. This means that the points on the graph of g(x) are twice as far from the x-axis compared to the corresponding points on the graph of f(x).

Shift up 4:

The term + 4 at the end of the equation indicates a vertical shift of 4 units upwards. This means that the graph of g(x) is shifted 4 units above the graph of f(x).

Combining these transformations, the correct description would be:

D. Reflection over the x-axis, stretch by a factor of 2, shift up 4.

Note: Choices C and D are not complete descriptions of the transformations since they do not mention the stretch factor of 2.

To know more about the equation indicates:- https://brainly.com/question/21052119

#SPJ11

The value of the given expression [\(87^3+ 13^3/87^2 -87 * 13 + 13^2\)] by simplifying the numerator and denominator using suitable identities is 100.

We will first calculate the numerator:

As  (\(a^3\) + \(b^3\)) = (a + b)(\(a^2\) - ab + \(b^2\)) :

\(87^3\) + \(13^3\) = (87 + 13)(\(87^2\) - \(87 * 13\) + \(13^2\))

= 100(\(87^2\) - 87 * 13 + \(13^2\))

Now, calculate the denominator:

\(87^2 - 87 * 13 + 13^2\)

As,(\(a^2 -2ab +b^2\)) =\((a - b)^2\):

\(87^2 - 87 * 13 + 13^2 = (87 - 13)^2\)

\(= 74^2\)

So by solving the equation further:

\((87^3+13^3) / (87^2- 87 * 13+13^2) = 100*(87^2- 87 *13 + 13^2)/(87^2 - 87 * 13 + 13^2)\)

As we can see the numerator and denominator are the same expressions (\(87^2 - 87 * 13 + 13^2\)). so, they cancel each other:

\((87^3 + 13^3) / (87^2 - 87 * 13 + 13^2) = 100\)

So, the value of the given expression is 100.

To know more about the expression:-

https://brainly.com/question/14083225

Answer:

6

Step-by-step explanation:

\(\sf 4-(-2)=4+2=\bf{6}\)

The answer is 6.

SOLUTION-

plotting on number line-

Know more about number line click here:

https://brainly.com/question/25230781

#SPJ2

the fund will be depleted after 11 payments.

To find out after how many payments the fund will be depleted, we need to determine the number of payments using the future value formula for an ordinary annuity.

The formula for the future value of an ordinary annuity is:

FV = P * ((1 + r)ⁿ - 1) / r

Where:

FV is the future value (total amount in the fund)

P is the payment amount ($5,294)

r is the interest rate per period (3.24% per annum compounded monthly)

n is the number of periods (number of payments)

We want to find the number of payments (n), so we rearrange the formula:

n = log((FV * r / P) + 1) / log(1 + r)

Substituting the given values, we have:

FV = $47,500

P = $5,294

r = 3.24% per annum / 12 (compounded monthly)

n = log(($47,500 * (0.0324/12) / $5,294) + 1) / log(1 + (0.0324/12))

Using a calculator, we find:

n ≈ 10.29

Since we need to round to the next payment, the fund will be depleted after approximately 11 payments.

Therefore, the fund will be depleted after 11 payments.

Learn more about future value here

https://brainly.com/question/30787954

#SPJ4

Answer:

0.315 per lb

Step-by-step explanation:

Answer:

A Rational

Step-by-step explanation:

Because 200 can be represented as 200/1, it shows that it can be made into a fraction unlike irrational numbers.

The F ratio in a completely randomized ANOVA is a) MSTR/MSE.

The F ratio in ANOVA is a measure of the variability between groups compared to the variability within groups. MSTR (mean square treatment) represents the variability between groups, while MSE (mean square error) represents the variability within groups.

The F ratio is the ratio of MSTR to MSE. A high F ratio indicates that the variability between groups is larger than the variability within groups, suggesting that there is a significant difference between at least two of the group means.

In contrast, a low F ratio suggests that there is little difference between group means, and any observed differences may be due to chance. Therefore, the F ratio is an essential statistic in ANOVA for determining the significance of the observed differences between groups.

For more questions like ANOVA click the link below:

https://brainly.com/question/23638404

#SPJ11

a). The difference between the two population means is estimated at a location to be 2.7.

b). 49 different possible outcomes make up the t distribution. The margin of error at 95% confidence is 1.7.

c). The range of the difference between the two population means' 95% confidence interval is (0.0, 5.4).

d). The (0.0, 5.4) represents the 95% confidence interval for the difference among the two population means.

The variability or spread in a set of data is commonly measured by the standard deviation. The deviation between the values in the data set and the mean, or average, value, is measured. A low standard deviation, for instance, denotes a tendency for data values to be close to the mean, whereas a high standard deviation denotes a larger range of data values.

Using the equation \(x_1-x_2\), we can determine the point estimate of the difference between the two population means. In this instance, we calculate the point estimate as 2.7 by taking the mean of Sample

\(1(x_1=22.8)\) and deducting it from the mean of Sample \(2(x_2=20.1)\).

With the use of the equation \(df=n_1+n_2-2\), it is possible to determine the degrees of freedom for the t distribution. In this instance, the degrees of freedom are 49 because \(n_1\) = 20 and \(n_2\) = 30.

We must apply the formula to determine the margin of error at 95% confidence \(ME=t*\sqrt[s]{n}\).

The sample standard deviation (s) is equal to the average of \(s_1\) and \(s_2\) (3.4), the t value with 95% confidence is 1.67, and n is equal to the

average of \(n_1\) and \(n_2\) (25). When these values are entered into the formula, we get \(ME=1.67*\sqrt[3.4]{25}=1.7\).

Finally, we apply the procedure to determine the 95% confidence interval for the difference between the two population means \(CI=x_1-x_2+/-ME\).

The confidence interval's bottom limit in this instance is \(x_1-x_2-ME2.7-1.7=0.0\) and the upper limit is \(x_1+x_2+ME=2.7+1.7=5.4\).

As a result, the (0.0, 5.4) represents the 95% confidence interval for the difference among the two population means.

To know more about standard deviations  click-

brainly.com/question/475676

#SPJ1

Answer:

joe mama 4life...... .....

the answer is 300020004000300002000010000043

Answer:

37x - 16y

Step-by-step explanation:

I added a photo of my solution

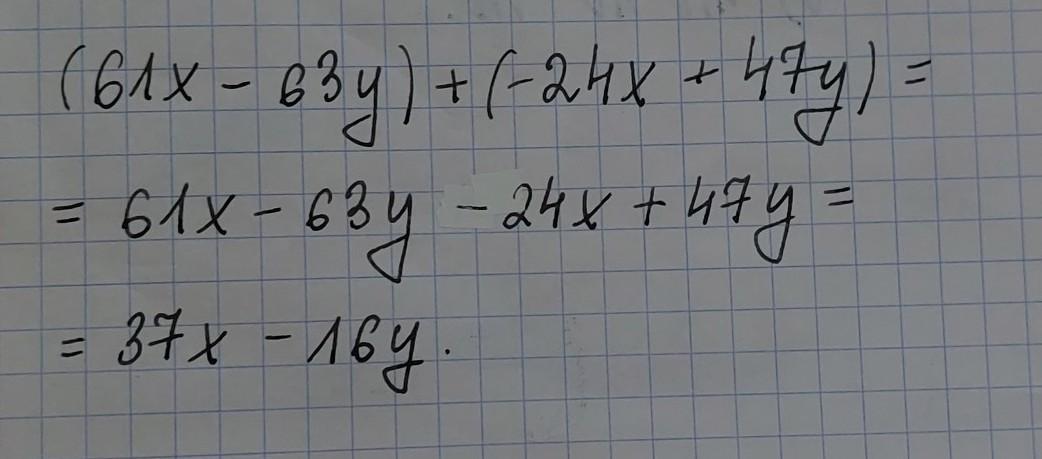
Answer:

Step-by-step explanation:

61x + 63y + -24x + 47y

Write the following equations in the form ax+b.

a) 4x+7+2x+5

Combine like terms: 4x+2x and 7+5

We get, 6x+12, which matches the form ax+b.

b) 4x-7+2x-5

Combine like terms: 4x+2x and -7-5

We get, 6x-12, which matches the form ax+b.

c) 4x-7-2x-5

Combine like terms: 4x-2x and -7-5

We get, 2x-12, which matches the form ax+b.

Answer:

Last answer is correct

Step-by-step explanation:

Parallel lines never meets...is the correct answer.

You should invest $22,627.84 if you want to receive payments of $3,000 at the end of each year for 10 years, with the first payment 3 years from now, if the money is compounded at 5% annually.

To solve this problem, we can use the present value formula for an ordinary annuity: PV = PMT * [1 - (1 + r)^-n] / r

Where:

PV = present value

PMT = periodic payment

r = interest rate

n = number of payments

In this case, we have:

PV = unknown

PMT = $3,000

r = 5%

n = 10 years (first payment in 3 years, so there are 10 payments after that)

Plugging these values into the formula,

we get:

PV = $3,000 * [1 - (1 + 0.05)^-10] / 0.05

PV = $22,627.84

Therefore, you should invest $22,627.84 if you want to receive payments of $3,000 at the end of each year for 10 years, with the first payment 3 years from now, if the money is compounded at 5% annually.

To know more about rate click here

brainly.com/question/14018365

#SPJ11

Answer:

13,849 books.

Step-by-step explanation:

The equation would be (69,678 - 430)/4 =  13,849

No solve this you have to multiply the cost per acre by the total are you want to plant:

It'll cost $73.3 to plant 2/3 of the acre.

There are 9 questions on the test.

Let, the number of multiple-choice questions on the test = m

the number of essay questions on the test = s

m + s = 26  .......(1)

So, We are also told that multiple choice is worth 3 points each, so the total number of points for m questions will be 3m.

As essays are worth 8 points each, so the total number of points for s questions will be 8s.

3m + 8s = 123 .......(2)

Now we will use the substitution method to solve a system of linear equations.

From equation (1) we will get,

m = 26 -s

Substituting this value in equation (2) we will get,

3 * (26- s) + 8s =123

78 - 3s + 8s = 123

5s = 123 -78

5s = 45

s = 45/5 = 9

So, there are 9 questions on the test.

Read more about the substitution method:

https://brainly.com/question/22340165

#SPJ4

The complete question is:

Ada’s history teacher wrote a test for the class.

The test is 26 questions long and is worth 123 points.

Ada wrote two equations, where m represents the

number of multiple choice questions on the test, and

s represents the number of essay questions on the test.

m+s= 26

3m + 8s = 123

How many essay questions are on the test?

The Poisson distribution is applied to events where the probability of occurrence of a certain number of events in a fixed interval of time, space, or distance is small but not necessarily "very small". False.

The Poisson distribution is used to model events that occur randomly and independently over a continuous or discrete interval of time, space, or distance, such as the number of phone calls received at a call center in an hour, the number of cars passing through a toll booth in a given time period, or the number of emails received per day. The Poisson distribution is characterized by a discrete probability mass function that describes the probability of a certain number of events occurring in a given interval, and it is widely used in probability theory and statistics for modeling events with low to moderate occurrence rates.

Learn more about “  probability of occurrence  “ visit here;

https://brainly.com/question/28320298

#SPJ4

The poisson distribution is applied to events for which the probability of occurrence over a given span of time, space, or distance is very small.

Given statement is False.

Because, The Poisson distribution is applied to events for which the probability of occurrence over a given span of time, space, or distance is not necessarily very small, but rather where the events occur randomly and independently at a constant average rate.

The Poisson distribution models the number of events that occur in a fixed time interval or within a certain area or volume of space, assuming that the events occur independently of each other and at a constant average rate. It is used in many fields, such as biology, physics, economics, and engineering, to model the occurrence of rare or common events.

The Poisson distribution has several important properties, including:

Its mean is equal to λ, and its variance is also equal to λ.

It is a discrete distribution, meaning that it models only whole numbers of events.

It is often used to model rare or unusual events, but can also be used for events that occur frequently, as long as they occur independently at a constant average rate.

For similar question on poisson distribution.

https://brainly.com/question/9123296

#SPJ11

(a) The average velocity for the time period beginning with t=2t=2 and

(1) lasting 0.5 seconds: -40 ft/s

(2) lasting 0.1 seconds: -88.4 ft/s

(3) lasting 0.05 seconds: -67.2 ft/s

(4) lasting 0.01 seconds: -64.36 ft/s

(b) The instantaneous velocity when t=2 is -24 ft/s.

(a) To find the average velocity for a given time period, we need to find the displacement during that time period and divide it by the duration of the time period.

(1) For the time period lasting 0.5 seconds, the initial time is t=2 and the final time is t=2.5. The displacement during this time period is:

\(y(2.5) - y(2) = (402.5 - 162.5^2) - (402 - 162^2) = -20 ft\)

The duration of the time period is 0.5 seconds. Therefore, the average velocity is:

average velocity = displacement / duration = -20 / 0.5 = -40 ft/s

(2) For the time period lasting 0.1 seconds, the initial time is t=2 and the final time is t=2.1. The displacement during this time period is:

\(y(2.1) - y(2) = (402.1 - 162.1^2) - (402 - 162^2) = -8.84 ft\)

The duration of the time period is 0.1 seconds. Therefore, the average velocity is:

average velocity = displacement / duration = -8.84 / 0.1 = -88.4 ft/s

(3) For the time period lasting 0.05 seconds, the initial time is t=2 and the final time is t=2.05. The displacement during this time period is:

\(y(2.05) - y(2) = (402.05 - 162.05^2) - (402 - 162^2) = -3.36 ft\)

The duration of the time period is 0.05 seconds. Therefore, the average velocity is:

average velocity = displacement / duration = -3.36 / 0.05 = -67.2 ft/s

(4) For the time period lasting 0.01 seconds, the initial time is t=2 and the final time is t=2.01. The displacement during this time period is:

\(y(2.01) - y(2) = (402.01 - 162.01^2) - (402 - 162^2) = -0.6436 ft\)

The duration of the time period is 0.01 seconds. Therefore, the average velocity is:

average velocity = displacement / duration = -0.6436 / 0.01 = -64.36 ft/s

(b) To find the instantaneous velocity when t=2, we need to find the derivative of the position function y(t) and evaluate it at t=2:

\(y(t) = 40t - 16t^2\)

y'(t) = 40 - 32t

y'(2) = 40 - 32(2) = -24 ft/s

Therefore, the instantaneous velocity when t=2 is -24 ft/s.

To know more about velocity, refer to the link below:

https://brainly.com/question/14509300#

#SPJ11

Answer:

Step-by-step explanation:  ma th w a y  b^2 t C^

Answer:

x = 15

Step-by-step explanation:

Using the Altitude- on- Hypotenuse theorem

(leg of large Δ )² = (part of hypotenuse below it ) × ( whole hypotenuse )

x² = 9 × (9 + 16) = 9 × 25 = 225 ( take square root of both sides )

x = \(\sqrt{225}\) = 15

Answer:

I did this quickly, so please check the logic.

I find x = 15

Step-by-step explanation:

See attached image.  Note that I've defined 3 triangles and their Pythagorean equations.  I also define a third line, RQ, as z.  Rearrange the equations and substitute in a way that allows elimination of all variables except x.

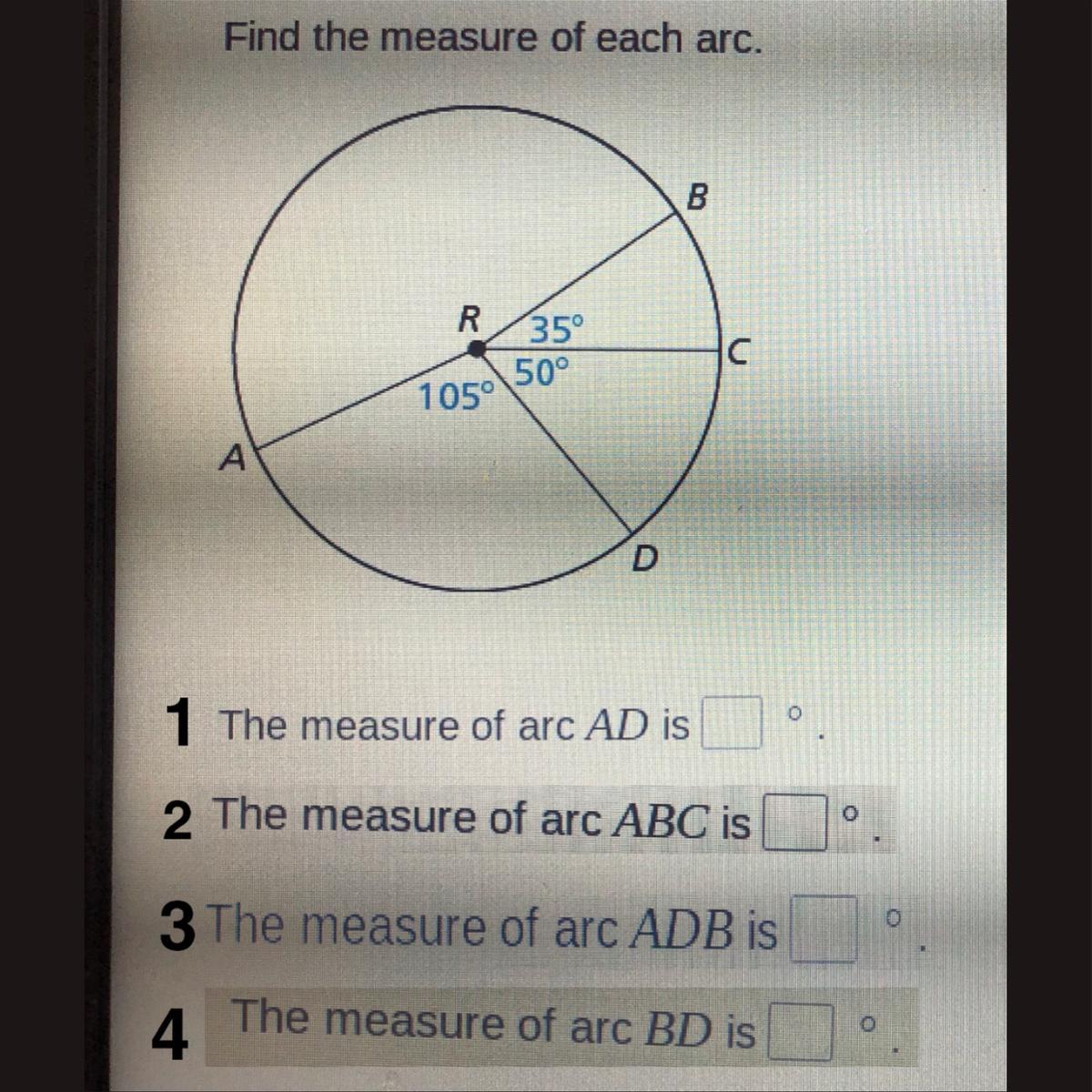
Answer:

See below

Step-by-step explanation:

The measure of all the arcs can be obtained by using 'Central angle and its corresponding arc theorem'.

1. The measure of arc AD is \( \boxed {105}\degree \)

2. The measure of arc ABC is \( \boxed {205}\degree \)

3. The measure of arc ADB is \( \boxed {190}\degree \)

4. The measure of arc BD is \( \boxed {85}\degree \)

The correct answer is D. setne 23 47. Based on the provided information, I understand that you have a comparison function in C code and its corresponding assembly code. You are asked to fill in the blanks by selecting the appropriate instructions based on the given values of a and b and the status flags SF, OF, ZF, and CF. Let's go through the options:

A. setg 47 23: This option is incorrect because setg is used to set a byte to 1 if the Greater flag (ZF=0 and SF=OF) is set, but the given values of a and b are 47 and 23, respectively, so it does not satisfy the condition for setg to be set.

B. setl 23 47: This option is incorrect because setl is used to set a byte to 1 if the Less flag (SF≠OF) is set, but the given values of a and b are 23 and 47, respectively, so it does not satisfy the condition for setl to be set.

C. sete 23 23: This option is incorrect because sete is used to set a byte to 1 if the Zero flag (ZF=1) is set, but the given values of a and b are 23 and 23, respectively, so it does not satisfy the condition for sete to be set.

D. setne 23 47: This option is correct. setne is used to set a byte to 1 if the Zero flag (ZF=0) is not set, which means the values of a and b are not equal. In this case, the given values of a and b are 23 and 47, respectively, so they are not equal, and setne should be used.

Therefore, the correct answer is D. setne 23 47

To know more about byte visit-

brainly.com/question/32309440

#SPJ11

\(answer \\ (3x - 5)(2x + 2) \\ solution \\ {6x}^{2} - 4x - 10 \\ = {6x}^{2} - (10 - 6)x - 10 \\ = {6x}^{2} - 10x + 6x - 10 \\ = 2x(3x - 5) + 2(3x - 5) \\ = (3x - 5)(2x + 2) \\ hope \: it \: helps\)

Answer:

x = 1⅔ or -1

Step-by-step explanation:

6x² -4x - 10

a=6, b=-4, c=-10, ac= -60

factors -10 & 6

6x² + 6x - 10x -10 =0

(6x² + 6x) - (10x - 10) =0

6x(x +1) - 10(x+1) =0

(6x-10)(x+1)=0

6x-10=0 or. x+1=0

6x= 10 or x= -1

x= 10/6 or. x= -1

x=1⅔ or x= -1

Marshall is wondering whether he can participate in the LLP again next year. The statement that is true is "He can participate in the LLP again, but only to the extent that his existing LLP balance is less than $20,000.

The Lifelong Learning Plan is a program that helps Canadian residents finance their post-secondary education through their registered retirement savings plans (RRSP). If an individual is attending school full-time, they can withdraw up to $10,000 a year from their RRSP under the program, or up to $20,000 in total. There are certain rules that must be followed by an individual participating in the LLP. For example, withdrawals must be made within four years of enrolling in an eligible educational program, and repayments must begin within the same period.

Here are the statements: Provided he repays his LLP balance in full by the end of this year, Marshall can participate in the LLP again next year.Marshall can only participate in the LLP once over his lifetime. However, his wife can make a LLP withdrawal from her RRSP on his behalf. He can participate in the LLP again, but only to the extent that his existing LLP balance is less than $20,000. He can only participate in the LLP a second time if he repays his LLP balance in full and waits 5 years before he returns to school.The correct statement is: He can participate in the LLP again, but only to the extent that his existing LLP balance is less than $20,000.

To know more about balance visit:

https://brainly.com/question/27154367

#SPJ11