A trapezoid has bases of lenghts 28 and 37. Find the trapezoids height if its area is 16
Answers
Answer:
0.49 ( Rounded to the hundredths place)
Step-by-step explanation:
The formula for a trapezoid's area is:
A = 1/2( b1 + b2)h
So let's plug in our digits:
16 = 1/2(28 + 37)h or 16 = 1/2(37 + 28)h
We add what is in the parathensis by following PEMDAS:
16 = 1/2(65)h
Then, multiply 1/2 (or 0.5) x 65
That equals 32.5. Now, divide both sides of the equation by 32.5. That cancels out on the right side, so we need to do 16/32.5. That equals ~0.49
Related Questions
Grace started her own landscaping business. She charges $16 an hour for mowing lawns and $25 for pulling weeds. In September she mowed lawns for 63 hours and pulled weeds for 9 hours. How much money did she earn in September?
Show your work
Answers
Answer:
$1,233
Step-by-step explanation:
Answer:
$1,233
Step-by-step explanation:
$16 an hour for mowing
$25 for pulling weeds
September - she mowed lawns for 63 hours and pulled weeds for 9 hours.
16(63) + 25(9) = $1,233
A person's muscle mass is expected to decrease with age. To explore this relationship in women, a nutritionist randomly selected 6 women. The results follow: X is age, and Y is a measure of muscle mass. X Y
43 106 47 97
41 106
47 92 48 92
46 113 Answer the following questions: 1. Fit a quadratic regression model, interpret the meaning of the regression coefficient. (2 Marks) [use R program to solve (X'X)^-1] 2. Test whether the quadratic term can be dropped from the regression model use a = 0.05. (2 Marks) [Hint: MSE = 47.086, SSR(x,x^2) = 230.74 and SSR(x) = 135.03] 3. Express the fitted regression function obtained in (1) in terms of the original variable X (1 Mark)
Answers
1. The quadratic regression model is \(Y = b0 + b1X + b2X^2\) . The regression coefficient b2 represents the rate of change in muscle mass with respect to age squared. 2. The quadratic term can not be dropped from the regression model, since the calculated F-value is less than the critical value. 3. The fitted regression function in terms of the original variable X is \(Y = 87.017 + 0.241X - 0.002X^2\).
To determine the quadratic regression model follow these steps:
1. Using R program, the quadratic regression model:
\(Y = b0 + b1X + b2X^2\)
where Y is the muscle mass, X is the age.
The regression coefficients are:
b0 = 283.962
b1 = -14.501
b2 = 0.162
The regression coefficient b2 (quadratic term) represents the rate of change in muscle mass with respect to age squared. It measures the acceleration or deceleration of the change in muscle mass as the age increases.
2. Using the F-test.
\(F = [SSR(x,x^2) - SSR(x)] / [(k - 1) * MSE]\)
where k = number of coefficients = 3 (b0, b1, b2).
MSE = Mean Squared Error = 47.086
\(SSR(x,x^2), SSR(x) =\) Sum of Squares due to Regression with both X and \(X^2\) as predictors = 230.74, due to Regression with only X as predictor = 135.03
Therefore,
\(F = [230.74 - 135.03] / [(3 - 1) * 47.086] = 2.214\)
Using a significance level the critical value for F-test is 5.143.
Since the calculated F-value (2.214) is less than the critical value (5.143), we fail to reject the null hypothesis. Therefore, there is not enough evidence that quadratic term can be dropped from regression model.
3. The fitted regression function in terms of the original variables:
\(Y = 87.017 + 0.241X - 0.002X^2\)
where X is the age and Y is the measure of muscle mass.
Know more about regression model here:
https://brainly.com/question/29657622
#SPJ11
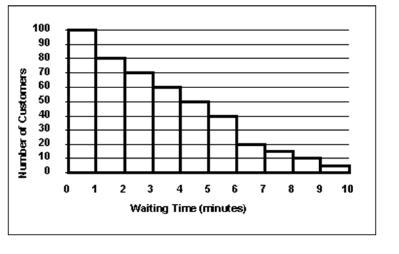
The staff of Mr. Wayne Wertz, VP of Operations at Portland Peoples Bank, prepared a frequency histogram of waiting time for walk-in customers. Approximately how many walk-in customers waited at least 6 minutes? (Note the position of the labels on the x-axis — the first column is the number of customers who waited 1 minute and the last column is the number of customers who waited 10 minutes)
Answers
The number of people who waited at least 6 minutes is given as follows:
50 people.
What is shown by the histogram?The height of each bin of the histogram represents the number of observations of the data-set in the desired interval.
The desired outcomes for this problem are given as follows:
Between 6 and 7 minutes: 20 people.Between 7 and 8 minutes: 15 people.Between 8 and 9 minutes: 10 people.Between 9 and 10 minutes: 5 people.Hence the number of people who waited at least 6 minutes is given as follows:
20 + 15 + 10 + 5 = 50 people.
More can be learned about histograms at brainly.com/question/25983327
#SPJ1
Function 1: Alan starts with $30 this week. He spends $5.30 per week. Let y be the amount remaining as a function of the number of weeks, X. 0 30 1 24.70 2 19.40 3 14.1
Answers
Answer:
y = 30 - 5.30x
Step-by-step explanation:
y-intercept: 30
slope: 5.30x
Just plug in the amount of weeks on x, and then subtract from 30.
PLEASE HELP COMPARING RATIOS

Answers
Answer:
8 minutes per customer in Restaurant One.
6 minutes per customer in Restaurant Two.
7 minutes per customer in Restaurant Three.
Restaurant Two had the fastest service.
Method:
I divided the time it took – for example – 48 divided by 6. I would do this because I wanted to find out each person took (6 people), and the amount of time it took for each person to get their food. I would use division for this problem because I am finding how much each person took out of the whole time.
Answer
The 2nd restaurant is the fastest
Step-by-step explanation:
I. Compare Time per Customers
When 1st restuarant = 48/6 = 9
2nd restuarant = 42/7 = 6
3rd restuarant = 63/9 = 7
Given if in 1 min, I can serve 20 customers = 1/20 = 0.05
in 1 min, He can serve 10 customers = 1/10 = 0.1
See the different? I can serve better than him.
So The answer is the 2nd restuarant.
Hope that help :D
The sum of the measures of the angles below is 180º.
(2x - 10)
X° (x + 10)
What is the measure of each angle? Write and solve an equation.

Answers
Sum of three angles=180°
\(\\ \rm\hookrightarrow x+x+10+2x-10=180\)
\(\\ \rm\hookrightarrow 4x=180\)
\(\\ \rm\hookrightarrow x=45\)
x+10=552x-10=80Round each fraction to help you estimate the solution for the following equation:1/6 + 5/6 = ____A. 0B. 1/2C. 1D. 2
Answers
The estimation of the equation 1/6 + 5/6 is 1 (option C).
For rounding a fraction to the nearest whole number, use the "rounding half up" rule if necessary.
To estimate the solution for the equation 1/6 + 5/6, we can round each fraction to the nearest whole number.
The fraction 1/6 is closer to 0 than it is to 1, so we will round it to 0.
The fraction 5/6 is closer to 1 than it is to 0, so we will round it to 1.
Now we can estimate the solution for the equation as follows:
0 + 1 = 1
Therefore, the estimated solution for the equation 1/6 + 5/6 is 1.
The correct answer is C. 1.
Learn more about rounding fractions here:
https://brainly.com/question/26623700
#SPJ11
factor out the gcf 12y³+10y²
Answers
Answer:
Find the prime factors of each term in order to find the greatest common factor (GCF).
2y^2
Factoring out the greatest common factor (GCF)To factor the GCF out of a polynomial, we do the following: Find the GCF of all the terms in the polynomial. Express each term as a product of the GCF and another factor. Use the distributive property to factor out the GCF.
Step-by-step explanation:
Hope it is helpful.....
The table shows how the length of a fish
changes over time.
Find the relationship between x, the time in
years, and y, the length in centimeters

Answers
Answer:
\(y=4.5\times x\)
Step-by-step explanation:
Solving;
\(y=4.5\times x\)
when x=3,
\(y=4.5\times3=13.5\) centimeters
when x=4
\(y=4.5\times4=18\) centimeters
when x=7
\(y=4.5\times7=31.5\) centimeters
when x=10
\(y=4.5\times10=45\) centimeters
Question content area top
Part 1
Find the value of x. 29
31
x
Question content area bottom
Part 1
x
enter your response here
(Round to the nearest tenth as needed. )
Help me solve thisView an example Get more help
Answers
the value of x is 29. Using the midpoint formula, we can find the value of x. The midpoint of 29 and 31 is the average of the two numbers:
midpoint = (29 + 31)/2 = 30
Since x is the midpoint of 30 and 31, we can set up an equation:
(x + 31)/2 = 30
Solving for x, we get:
x + 31 = 60
x = 29
Therefore, the value of x is 29.
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
To know more about midpoint formula, visit: brainly.com/question/30242987
#SPJ4
A ball is thrown vertically upward. Its height h(t) after t second-is h(t)=100t-16t². a) Find the velocity and acceleration at 1 seconds. b) What is the ball's height when it is going down at rate of 10 feet per second? c) When the ball was speeding up? Explain. 7 Find the derivative of fand then find the domains of fand f'if f(x)=ln(9x-x³)
Answers
a) Velocity at 1 second: 68 ft/s ,Acceleration at 1 second: -32 ft/s² b) Height when the ball is going down at a rate of 10 ft/s: Approximately 151.5625 ft. c) The ball never speeds up during its motion.
a) To find the velocity and acceleration at 1 second, we need to differentiate the height function h(t) with respect to time.
Given: h(t) = 100t - 16t²
Velocity (v(t)) is the derivative of height with respect to time:
v(t) = dh(t)/dt
Differentiating h(t) with respect to t:
dh(t)/dt = d(100t - 16t²)/dt = 100 - 32t
To find the velocity at 1 second, substitute t = 1 into the velocity equation:
v(1) = 100 - 32(1) = 100 - 32
= 68 ft/s
Acceleration (a(t)) is the derivative of velocity with respect to time:
a(t) = dv(t)/dt
Differentiating v(t) with respect to t: dv(t)/dt = d(100 - 32t)/dt = -32
To find the acceleration at 1 second, substitute t = 1 into the acceleration equation: a(1) = -32 ft/s²
b) To find the ball's height when it is going down at a rate of 10 feet per second, we need to find the time (t) when the velocity (v(t)) is equal to -10 ft/s. We can set up the equation: v(t) = -10
Substituting the expression for v(t) from earlier: 100 - 32t = -10
Rearranging the equation: 32t = 110
Solving for t: t = 110/32 ≈ 3.4375 seconds
To find the height at t = 3.4375 seconds, substitute this value into the height equation:
h(3.4375) = 100(3.4375) - 16(3.4375)² ≈ 343.75 - 192.1875 ≈ 151.5625 ft
Therefore, the ball's height when it is going down at a rate of 10 feet per second is approximately 151.5625 feet.
c) The ball is speeding up when the velocity (v(t)) is increasing. To determine when this occurs, we need to find the critical points of the velocity function.
Setting the derivative of v(t) equal to zero:
dv(t)/dt = -32 = 0
Solving for t: -32 = 0 (No solution)
Since there are no solutions to dv(t)/dt = 0, the velocity function does not have any critical points. This means the velocity is always decreasing (due to the negative acceleration of -32 ft/s²) and the ball is always slowing down. Therefore, the ball never speeds up during its motion.
Learn more about derivative here: https://brainly.com/question/32963989
#SPJ11
what amount of fuel reserve must be carried on a day vfr flight?. minutes about how many gallons would that be for a piper archer? gallons
Answers
Answer:
For a day VFR flight in a Piper Archer, you would need a fuel reserve of approximately 5 gallons.
Step-by-step explanation:
The amount of fuel reserve that must be carried on a day VFR (Visual Flight Rules) flight, the FAA requires a minimum fuel reserve of 30 minutes at cruising speed for day VFR flights. To calculate the gallons needed for a Piper Archer, follow these steps:
1. Determine the fuel consumption rate of the Piper Archer at cruising speed, which is typically around 10 gallons per hour (GPH).
2. Divide the required fuel reserve minutes (30) by the minutes in an hour (60): 30 / 60 = 0.5 hours.
3. Multiply the fuel consumption rate (10 GPH) by the required fuel reserve time in hours (0.5 hours): 10 * 0.5 = 5 gallons.
Therefore, for a day VFR flight in a Piper Archer, you would need a fuel reserve of approximately 5 gallons.
learn more about "fuel reserve":-https://brainly.com/question/31663770
#SPJ11
Linear Inequality Word Problems A widget manufacturer starts their business off by spending $200 to design a new product. They plan to sell that product for $50 each. How many products will they need to sell to make a profit of no less than $200?
Answers
Answer:
4 or 8, depending on how you interpret the questions
Step-by-step explanation:
In order to break even, they have to sell 4 widgets. In other words, to make back the $200 they spent on design, they have to sell 4 widgets. Anything over that is profit. This assumes the entire $50 selling price goes to profit (no other information was given).
x = number of widgets
50x ≥ 200
x ≥ 4
To make another $200 above the break even, they have to sell 4 more widgets for a total of 8.
when to use the one mean Z test for small samples of size less than 15
Answers
The one mean Z test can be used for small samples of size less than 15 when the population standard deviation is known.
The one-mean z-test is a hypothesis test that is used to test a hypothesis about the mean of a population when the population standard deviation is known, and the sample size is large (typically greater than 30).
When the sample size is small (less than 15), the one-mean z-test is not appropriate because the assumptions of the test may not be met.
When the sample size is small, we typically use a t-test instead of a z-test to test a hypothesis about the population mean.
Specifically, we use a one-sample t-test when the population standard deviation is unknown, and the sample size is small (typically less than 30).
The one-sample t-test uses a t-distribution to calculate the p-value and test the null hypothesis about the population mean.
It is important to note that the sample size of 15 is not a hard and fast rule for when to switch from the z-test to the t-test.
The decision of which test to use depends on the specific context and the assumptions of the test.
In general, if the population standard deviation is unknown and the sample size is small (less than 30), then we use the t-test. If the population standard deviation is known and the sample size is large (greater than 30), then we use the z-test.
For similar question on Z test:
https://brainly.com/question/15683598
#SPJ11
What expression is equivalent to: 4z x 2y
O 8 (z + y)
8zy
-8zy
O 8(xy)
Answers
Answer:
8 (z+y)
Step-by-step explanation:
Hope i helped you
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11
How do you translate coordinates?
Answers
To translate an entire triangle, find the coordinates of each of the triangle's vertices, add the horizontal translation then plot the three translated points.
Whenever an object is moved from one location to the next without changing its size, shape, or orientation, a translation takes place. If we know which way and how far the figure to be moved, we can draw the translation in the coordinate plane.
Use P′(x+a,y+b) to translate the point P(x,y), a unit to the right, and b unit up. Use P′(x−a,y−b) to translate the point P(x,y), a unit to the left and b unit to the lower.
There are some steps of translating the triangle:
Step 1: Find the coordinates of each of the triangle's vertices in step one.
Step 2: Add the horizontal translation value to each vertex's x-coordinate and the vertical translation value to each point's y-coordinate to translate each point. If the horizontal translation is to the left or the vertical translation is downward for these translations, add a negative number.
Step 3: Plot the three translated points and draw the triangle by drawing a straight line between each pair of points.
To learn more about translation of triangle link is here
brainly.com/question/3096197
#SPJ4
Determine whether line AB and line CD are parallel, perpendicular, or neither.
A(-6,-9), b8,19), C(0,-4), D(2,0)
please and thank you
Answers
Answer:
line AB is parallel to line CD
Step-by-step explanation:
Because they have the same gradient which is 2
Find the critical t-value that corresponds to 90% confidence. Assume 16 degrees of freedom. (Round to three decimal places as needed.)
Answers
1.746 is the critical t value that corresponds to 90% confidence.
To find the critical t-value that corresponds to 90% confidence with 16 degrees of freedom, follow these steps:
1. Determine the desired confidence level: 90%
2. Calculate the corresponding significance level (alpha) by subtracting the confidence level from 100%: 100% - 90% = 10%
3. Divide the significance level by 2 to get the value for a two-tailed test: 10% / 2 = 5%
4. Look up the critical t-value in a t-distribution table using the degrees of freedom (16) and the 5% value.
From the t-distribution table, the critical t-value for 16 degrees of freedom and 90% confidence is approximately 1.746.
So, the CRITICAL T VALUE that corresponds to a 90% CONFIDENCE level with 16 DEGREES FREEDOM is 1.746, rounded to three decimal places.
LEARN MORE ON CRITICAL T VALUE:
https://brainly.com/question/28159026
#SPJ11
Write the system x' = e³tx − 2ty +3 sin(t), y' = 8 tan(t) y + 3x − 5 cos (t) in the form d = P(t) [ * ] + ƒ (t). dty Use prime notation for derivatives and write a and à ʼ, etc., instead of æ(t), î '(t), or da. ]-[ = ][ +
Answers
The given system of equations x' = \(e^{(3t)}\)x - 2ty + 3sin(t), y' = 8tan(t)y + 3x - 5cos(t) can be written as:
\(\frac{d}{d t}=\left[\begin{array}{cc}e^{3 t} & 2 t \\-2 t & -e^{3 t}\end{array}\right]\left[\begin{array}{l}x \\y\end{array}\right]+\left[\begin{array}{c}3 \sin (t) \\-5 \cos (t)\end{array}\right]\)
The system of equations is given by:
x' = \(e^{(3t)}\)x - 2ty + 3sin(t)
y' = 8tan(t)y + 3x - 5cos(t)
To write the system in the desired form, we first rearrange the equations as follows:
x' - \(e^{(3t)}\)x + 2ty = 3sin(t)
y' - 3x - 8tan(t)y = -5cos(t)
Now, we can identify the coefficients and functions in the system:
P(t) = \(e^{3t}\)
q(t) = 2t
f₁(t) = 3sin(t)
f₂(t) = -5cos(t)
Using this information, we can rewrite the system in the desired form:
x' - P(t)x + q(t)y = f₁(t)
y' - q(t)x - P(t)y = f₂(t)
Thus, the system can be written as:
\(d=\left[\begin{array}{l}x^{\prime} \\y^{\prime}\end{array}\right]=\left[\begin{array}{cc}P(t) & q(t) \\-q(t) & -P(t)\end{array}\right]\left[\begin{array}{l}x \\y\end{array}\right]+\left[\begin{array}{l}f_1(t) \\f_2(t)\end{array}\right]\)
In the given notation, this becomes:
d = P(t) [ * ] + f(t)
where [ * ] represents the coefficient matrix and f(t) represents the vector of functions.
The complete question is:
"Write the system
x' = \(e^{(3t)}\)x - 2ty + 3sin(t)
y' = 8tan(t)y + 3x - 5cos(t)
in the form d/dt=P(t) [ * ] + ƒ (t).
Use prime notation for derivatives."
Learn more about equations:
https://brainly.com/question/22688504
#SPJ11
A variable expression consists of numbers, variables, and operations.
true or false
Answers
Answer:
True
Step-by-step explanation:
Last year frank had a total income of $58,800. he sold a house and made a profit of $27,940. he also had monthly income of $80 from investments. assuming frank works 25 hours per week and 52 weeks per year as an hourly employee, how much more an hour would frank had to have earned last year in order to have a total income of $59,970? a. $0.63 b. $0.72 c. $0.80 d. $0.90 please select the best answer from the choices provided a b c d
Answers
You had to earn $0.90 more an hour last year in order to have a total income of $59,970.
The correct option is D.
The unitary method is a method for solving a problem by the first value of a single unit and then finding the value by multiplying the single value.
Last year,
The Total income = $58,800
The Profit made by selling the house =$27,940
The Monthly income by investment = $80
The Yearly income by investment = 12(80) ( 1 year = $80)
= $960
Also, 25 hours per week and 52 weeks per year as an hourly employee.
Let x be your hourly wages.
Then, yearly income by working = 25 x 52 x X
= 1300x
As per the given,
1300x + 960 + 27,940 = 58,800
1300x = 29900
x = 23
In order to earn a total income of $59,970, we have
1300x + 960 + 27,940 = 59,970
x = 23.9
Difference = 23 -23.9= $ 0.90
Hence, You had to earn $0.90 more an hour last year in order to have a total income of $59,970.
Learn more about the unitary method here https://brainly.com/question/23423168
#SPJ4
Answer:
Step-by-step explanation:
the answer is d
Prove that if H is a normal subgroup of G of prime index p then for all K < G either (1) K < H or (ii) G = HK and |K : K n H|= p.
Answers
If H is a normal subgroup of G of prime index p then for all K < G either (i) K < H or (ii) G = HK and |K : K ∩ H|= p.
Consider H as a normal subgroup of G with index p, where p is a prime number.
Let K be an arbitrary subgroup of G.
Observe the double coset decomposition of K relative to H, which is the collection of double cosets of the form HaK, where a is an element of G.
The decomposition can be represented as:
G = ⨆ (HaK), where the union is over distinct double cosets.
Note that H(K ∩ H) is one of the double cosets in this decomposition.
Since H is normal in G, we have:
H(K ∩ H) = K(H ∩ K) = K ∩ H
Now, consider the index [K: K ∩ H].
By the Second Isomorphism Theorem, we know that:
[K : K ∩ H] = [KH : H]
Since H has prime index p in G, [KH: H] must be a divisor of p.
Thus, the possible values of [KH: H] are 1 or p.
If [KH: H] = 1, this implies that KH = H.
Since K is a subgroup of KH, we have K < H, which corresponds to case (i).
If [KH: H] = p, then we have:
|K: K ∩ H| = p
By the Second Isomorphism Theorem, this also implies that G = HK, which corresponds to case (ii).
Thus, we have shown that for all K < G, either (i) K < H or (ii) G = HK and |K: K ∩ H| = p.
Learn more about isomorphism:
https://brainly.com/question/29561611
#SPJ11
Mt. Young bought some hamburgers for his cookout. The price was $32,17, but, le found that hamburger parties were on special for $22.692. What was hubs DOcent Bio
A $3.20
B. 29.68%
OC45%
D. $87.25
Answers
A is too little
C is too much off
D is way too much
So B is your answer
7-4 skills practice solving logarithmic equations and inequalities1. 3x = log6 216 2. x - 4 = log3 243 3. log4 (4x - 20) = 54. log9 (3 - x) = log9(5x – 15) 5. log81 (x + 20) = log81 (6x) 6. log9 (3x2) = log9 (2x + 1)7. log4(x - 1) = log4(12) 8. log7(5 - x) = log7 (5) 9. logx (5x) = 2
Answers
Solution to given logarithmic equations and inequalities are;
x = 1
x = 9
x = 261
x = 10/3
x = 4
3x² - 2x - 1 = 0
x = 1 or x = -1/3
x = 13
x = 0
x = 0 or x = 5
How to evaluate each part of the qustion?1. 3x = log6 216
Using the definition of logarithm, we have:
\(6^{3x} = 216\)
\(6^{3x} = 6^3\)
3x = 3
x = 1
2. x - 4 = log3 243
Using the definition of logarithm, we have:
\(3^{x - 4} = 243\)
\(3^{x - 4} = 3^5\)
x - 4 = 5
x = 9
3. log4 (4x - 20) = 5
Using the definition of logarithm, we have:
4⁵ = 4x - 20
1024 = 4x - 20
4x = 1044
x = 261
4. log9 (3 - x) = log9(5x – 15)
Using the property of logarithms that states that if log a b = log a c, then b = c, we have:
3 - x = 5x - 15
20 = 6x
x = 10/3
5. log81 (x + 20) = log81 (6x)
Using the property of logarithms that states that if log a b = log a c, then b = c, we have:
x + 20 = 6x
20 = 5x
x = 4
6. log9 (3x²) = log9 (2x + 1)
Using the property of logarithms that states that if log a b = log a c, then b = c, we have:
3x² = 2x + 1
3x² - 2x - 1 = 0
7. Using the quadratic formula, we have:
x = (-(-2) ± √((-2)² - 4(3)(-1))) / (2(3))
x = (2 ± √(16)) / 6
x = (2 ± 4) / 6
x = 1 or x = -1/3
8. log4(x - 1) = log4(12)
Using the property of logarithms that states that if log a b = log a c, then b = c, we have:
x - 1 = 12
x = 13
9. log7(5 - x) = log7 (5)
Using the property of logarithms that states that if log a b = log a c, then b = c, we have:
5 - x = 5
x = 0
10. logx (5x) = 2
Using the definition of logarithm, we have:
x² = 5x
x² - 5x = 0
x(x - 5) = 0
x = 0 or x = 5
Note that x = 0 is not a valid solution, since log 0 is undefined. Therefore, the only solution is x = 5.
Learn more about logarithmic equations.
brainly.com/question/29094068
#SPJ11
What test to see if the difference between groups is statistically significant?
Answers
The level of significance, typically set at 0.05, is used to determine whether the observed difference is statistically significant or simply due to chance
To determine whether the difference between groups is statistically significant, you would typically use a hypothesis test such as a t-test, ANOVA (analysis of variance), or a chi-square test. These tests are used to compare the means or proportions of different groups and calculate the probability of obtaining the observed difference by chance. The level of significance, typically set at 0.05, is used to determine whether the observed difference is statistically significant or simply due to chance. To determine if the difference between groups is statistically significant, you can use a hypothesis test called the t-test. The t-test compares the means of two groups and takes into account the sample size and variance within each group. This test helps you determine if there is a significant difference between the groups or if the observed difference is due to random chance.
learn more about level of significance
https://brainly.com/question/13947717
#SPJ11
.........................
Answers
Answer:
.............................................
Answer:
......................................
The graph of y=f(x) is shown on the grid. The graph G is a translation of the graph y=f(x)

Answers
The translated function is:
G(x) = f(x) - 1
b) The maximum of y = 2*f(x) is the point (0, 8).
How to write the equation of the translated function?
We know that G(x) is a translation of f(x), and the graph of G(x) is the pink one.
We can see that it is 1 unit below f(x), then we have a translation of one unit downwards, so we can write:
G(x) = f(x) - 1
This is the rule for G(x).
b) If the maximum of f(x) is (0, 4), then:
f(0) = 4
The maximum of 2*f(x) is also at x = 0, we will get:
2*f(0) = 2*4 = 8
So the maximum here is (0, 8).
Learn more about translations:
https://brainly.com/question/24850937
#SPJ1
show that 3/5 is bigger than 4/9
Answers
Answer: 27/45 > 20/45
Step-by-step explanation:
You must make the denominator of each fraction equivalent while keeping the value of each individual fraction the same.
3/5 x (9/9) = 27/45
4/9 x (5/5) = 20/45
27/45 > 20/45
Answer: 27/45 > 20/45
Step-by-step explanation:
You must make the denominator of each fraction equivalent while keeping the value of each individual fraction the same.
3/5 x (9/9) = 27/45
4/9 x (5/5) = 20/45
27/45 > 20/45
The ratio of boy to girl who play kickball at rece i 6 to 2. There are 18 girl on the team. What i the nu
mber of boy who play kickball at rece?
Answers
The ratio of boy to girl who play kickball at race is 6 to 2. There are 18 girl on the team. the number of boys who play kickball at race is 12 boys.
The ratio of boy to girl who play kickball at race is 6 to 2
6 boys: 2 girls
Multiply the number of girls by the ratio:
18 girls x (6 boys / 2 girls) = 18 x 3 = 54
Subtract the number of girls from the total to get the number of boys:
54 - 18 = 36
Therefore, there are 12 boys who play kickball at race.
Learn more about ratio here
https://brainly.com/question/13419413
#SPJ4