a t-shirt at the mall has an origanal price of 35. if it is on sale for 30% off how much money will u save
Answers
Answer:
You will save $10.50
Step-by-step explanation:
Take 30% of 35:
35(0.30) = 10.5
Therefore, you will save $10.50
Additionally, the sale price would be $35 - $10.50 = $24.50
Answer:
15
Step-by-step explanation:
Related Questions
Question 6 Multiple Choice Worth 1 points)
(01.06 LC)
Solve x - 5y = 6 for x.
Answers
Answer:
x = 6+5y
Step-by-step explanation:
x - 5y = 6
Add 5y to each side
x - 5y+5y = 6+5y
x = 6+5y
Answer:
x = 6 + 5y
Step-by-step explanation:
x - 5y = 6
Solve for x.
x - 5y = 6
Add 5y to both side
x - 5y + 5y = 6 + 5y
x = 6 + 5y
What 98 x 8 divided by 2 and what is this game called

Answers
Answer:
392 and Overwatch I think
Step-by-step explanation:
Answer:
392 and overwatch, the other guy deleted his answer soo imma hop in here and put the answer.
Step-by-step explanation:
Peter has to spend $9000 on expenses each year. If that amount of money is 60% of his salary, then how much money does Peter make working as an administrator per year?
Answers
Answer:
Step-by-step explanation:
9000 is 60% of what number?
9000=0.6*X
9000/0.6=X
X=$15000
Please hurryyyyy !!!! What's the slope and y intercept of 4y = 2x - 12
Answers
Answer:
slop is 0.5 and intercept of y is -3
Answer:
½ is the slope,-3 is the intercept
Step-by-step explanation:
now to find the slope and intercept
we use the equation,
y=mx + c
where m is the slope
and c is the y intercept
so we compare 4y=2x-12 to the equation
but we first have to make y the subject of the equation in the question – 4y is already the subject –
y=2x-12/4
y=2x/4 -3
comparing...
we see that m is 2/4=½ c= -3
Choose the correct simplification of the expression −4x2(6x − 5x2 − 5). 20x4 24x3 20x2 −9x4 2x3 − 9x2 20x4 − 24x3 20x2 −20x4 24x3 − 20x2.
Answers
Answer: 20x4−24x3+20x2
Step-by-step explanation:
when simplifying you first distribute the -4x^2. This will result in -24x^3, 20x^4, and 20x^2
Answer:
20 x^4 - 24 x^3 + 20 x^2 is the only correct answer however not the best simplification.
Step-by-step explanation:
Simplify the following:
-4 x^2 (-5 x^2 + 6 x - 5)
Hint: Factor a minus sign out of -5 x^2 + 6 x - 5.
Factor -1 out of -5 x^2 + 6 x - 5:
-4 x^2×(-(5 x^2 - 6 x + 5))
Hint: Multiply -4 and -1 together.
-4 (-1) = 4:
Answer: 4 x^2 (5 x^2 - 6 x + 5)
Solve for n.
2/3 (1 + n ) = -1/2n
Answers
Answer: -4/7
Step-by-step explanation:
2/3 (1 + n ) = -1/2n
2/3 + 2/3n = -1/2n
Multiply both sides by 6
4 + 4n = -3n
4n + 3n = -4
7n = -4
Divide both sides by 7
n = -4/7
Answer:
Answer above its explained fully


according to the information that comes with a certain prescription drug, when taking this drug, there is a 23% chance of experiencing nausea (n) and a 52% chance of experiencing decreased sexual drive (d). the information also states that there is a 12% chance of experiencing both side effects. what is the probability of experiencing neither of the side effects?
Answers
the probability of experiencing neither side effect is 0.37 or 37%.let's denote the probability of experiencing nausea by P(n) and the probability of experiencing decreased sexual drive by P(d). We know that:
P(n) = 0.23
P(d) = 0.52
P(n ∩ d) = 0.12
We want to find the probability of experiencing neither side effect, which can be denoted by P(~n ∩ ~d), where ~n and ~d represent the complements of nausea and decreased sexual drive, respectively.
We can use the formula for the probability of the union of two events to find P(~n ∪ ~d):
P(~n ∪ ~d) = 1 - P(n ∪ d)
We know that P(n ∪ d) = P(n) + P(d) - P(n ∩ d), so we can substitute the given values to get:
P(n ∪ d) = 0.23 + 0.52 - 0.12 = 0.63
Therefore,
P(~n ∪ ~d) = 1 - 0.63 = 0.37
So the probability of experiencing neither side effect is 0.37 or 37%.
To learn more about probability click here:brainly.com/question/32117953
#SPJ11
Plsss Help Urgent!!! Which point represents the person who practiced the most and got the fastest time in a swim meet?
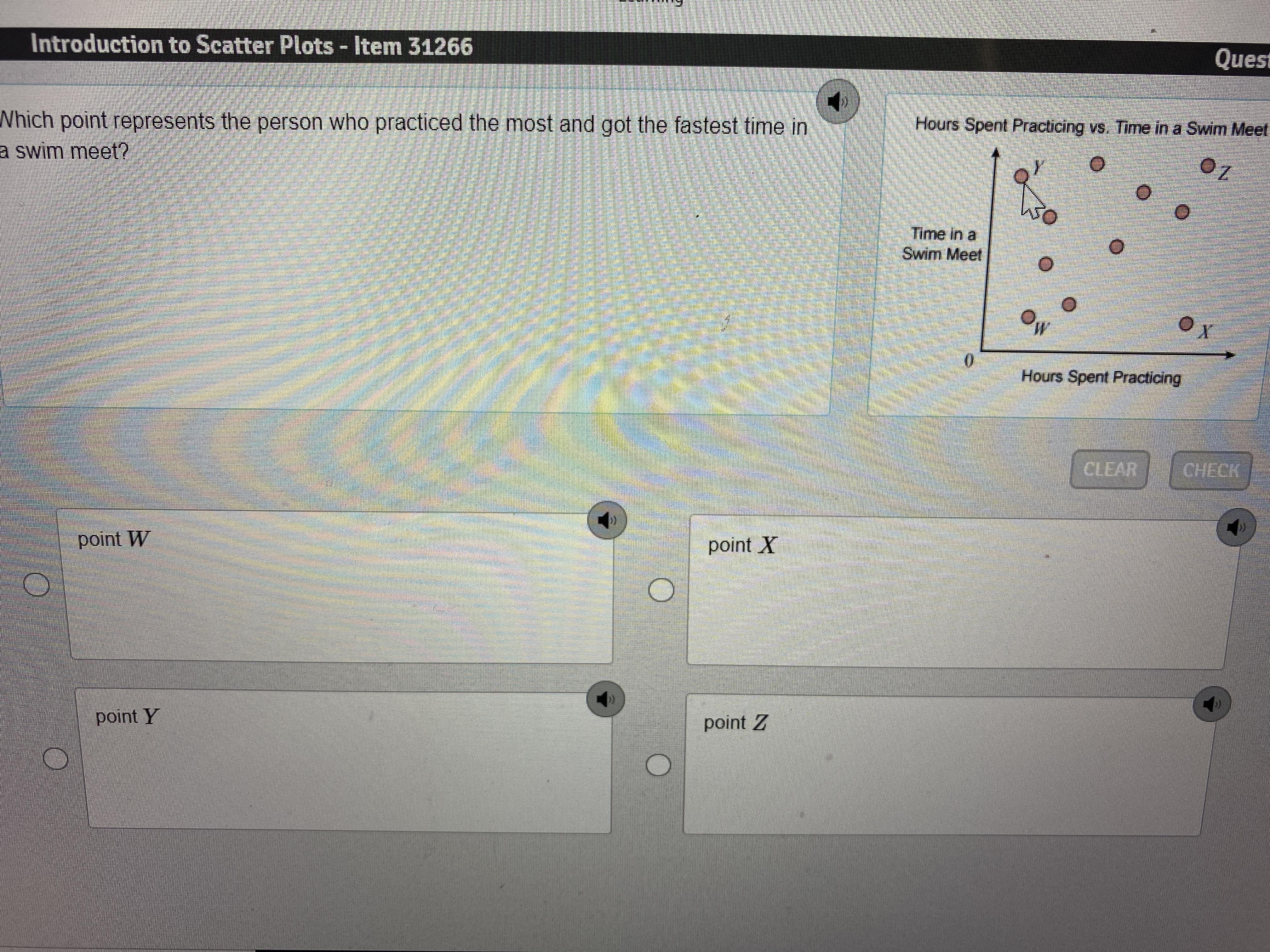
Answers
Answer:
Point X
Step-by-step explanation:
N is between M and P . MN = 17, NP= 3y , and MP = 5y + 9 . Find the measure of MP
Answers
Answer:
MP = 29
Step-by-step explanation:
5y + 9 = 3y + 17
2y = 8
y = 4
5(4) + 9 = 29
Which describe all decimal that te rational number
Answers
Explanation: Any decimal number that terminates or ends at some point is a rational number.
the starting number is $42.51 please help me with math

Answers
Answer:
The answer is a).
Step-by-step explanation:
$42.51 + $4.25 = $46.76
Use a familiar formula from geometry to find the length of the curve described and then confirm using the definite integral. r=5sinθ+7cosθ,0≤θ≤π. Area =
Answers
We have the, r = 5sinθ + 7cosθ. In order to find the length of the curve, we need to use a familiar formula from geometry.
A familiar formula from geometry is the formula for the length of an arc of a circle.
Let's start by first finding an expression for r².
\(We have,r = 5sinθ + 7cosθr² = (5sinθ + 7cosθ)²= 25sin²θ + 49cos²θ + 70sinθcosθ\)
\(Now, using the formula for the length of an arc of a circle, we have:L = ∫[0,π]√(r² + (dr/dθ)²) dθ\)
\(Putting the value of r² in the above equation, we have:L = ∫[0,π]√(25sin²θ + 49cos²θ + 70sinθcosθ + (dr/dθ)²) dθ\)
\(Differentiating r w.r.t. θ, we get,dr/dθ = 5cosθ - 7sinθ\)
\(We put this value in the above equation to get, L = ∫[0,π]√(25sin²θ + 49cos²θ + 70sinθcosθ + (5cosθ - 7sinθ)²) dθ\)
\(Simplifying the above expression, L = ∫[0,π]√(74 + 60sinθcosθ) dθ\)
\(Using the trigonometric identity, 2sinθcosθ = sin2θ, we have:L = ∫[0,π]√(74 + 30sin2θ) dθ\)
\(Now, we can substitute sin2θ = (1/2)(1 - cos2θ) to get:L = ∫[0,π]√(119 - 45cos2θ) dθ\)
\(Let's use a substitution, u = cos2θdu = -2sin2θ dθ\)
To integrate the above expression, we need to have an extra factor of 2sin2θ which we can obtain using the substitution above.
\(Hence, we have:L = ∫[1,-1]√(119 - 45u) (-1/2sinθ) duL = (-1/2) ∫[1,-1]√(119 - 45u) / √(1 - u²) du\)
\(Using the substitution, u = cosθ, we have:L = (-1/2) ∫[0,π]√(119 - 45cosθ) d(cosθ)L = (-1/2) ∫[0,π]√(119 - 45cosθ) dθ [Since cosθ is a decreasing function in [0,π]]\)
\(Now, we have,L = (-1/2) [F(π) - F(0)] where F(θ) = (2/3)[119sinθ - 15cosθ√(119 - 45cosθ) + 45cosθsinθ]\)
\(Putting the limits, we get, L = (-1/2) [(2/3)[119sin(π) - 15cos(π)√(119 - 45cos(π)) + 45cos(π)sin(π)] - (2/3)[119sin(0) - 15cos(0)√(119 - 45cos(0)) + 45cos(0)sin(0)]]L = (2/3)[119 + 15√74] = 108.03 (approx)\)
We can verify our answer using the definite integral.
Let's first find an expression for ds², where ds is the infinitesimal length of the curve.
\(We have,ds² = dr² + r²dθ² = (5cosθ - 7sinθ)²dθ² + (5sinθ + 7cosθ)²dθ²ds² = 74 + 60sinθcosθdθ²\)
\(Using this, we have, Area = ∫[0,π] ds = ∫[0,π] √(74 + 60sinθcosθ) dθ\)
This is the same integral that we obtained earlier.
Hence, the area is 108.03 (approx).
To know more about the word expression visits :
https://brainly.com/question/23246712
#SPJ11
The length of the curve is indeed \(\(\sqrt{74}\pi\)\), which matches our earlier result.
To find the length of the curve described by the polar equation
\(\(r = 5\sin(\theta) + 7\cos(\theta)\)\),
where \(\(0 \leq \theta \leq \pi\)\), we can use a familiar formula from geometry known as the arc length formula for polar curves.
The arc length formula for a polar curve is given by:
\($\[S = \int_{\theta_1}^{\theta_2} \sqrt{r^2 + \left(\frac{{dr}}{{d\theta}}\right)^2} d\theta\]\)
In this case, we have
\(\(r = 5\sin(\theta) + 7\cos(\theta)\)\)
so we need to calculate \(\(\frac{{dr}}{{d\theta}}\)\)
Differentiating (r) with respect to \(\(\theta\)\), we get:
\(\[\frac{{dr}}{{d\theta}} = \frac{{d}}{{d\theta}}(5\sin(\theta) + 7\cos(\theta))\]\)
\(\[= 5\cos(\theta) - 7\sin(\theta)\]\)
Now, we can substitute the values into the arc length formula:
\($\[S = \int_{0}^{\pi} \sqrt{(5\sin(\theta) + 7\cos(\theta))^2 + (5\cos(\theta) - 7\sin(\theta))^2} d\theta\]\)
Simplifying the expression inside the square root:
\(\[(5\sin(\theta) + 7\cos(\theta))^2 + (5\cos(\theta) - 7\sin(\theta))^2\]\)
\(\[= 25\sin^2(\theta) + 70\sin(\theta)\cos(\theta) + 49\cos^2(\theta) + 25\cos^2(\theta) - 70\sin(\theta)\cos(\theta) + 49\sin^2(\theta)\]\)
\(\[= 74\sin^2(\theta) + 74\cos^2(\theta)\]\)
\(\[= 74(\sin^2(\theta) + \cos^2(\theta))\]\)
\(\[= 74\]\)
Now, the integral becomes:
\($\[S = \int_{0}^{\pi} \sqrt{74} d\theta\]\)
Since \(\(\sqrt{74}\)\) is a constant, it can be moved outside the integral:
\($\[S = \sqrt{74} \int_{0}^{\pi} d\theta\]\)
Evaluating the integral:
\($\[S = \sqrt{74} [\theta]_{0}^{\pi}\]\)
\(\[S = \sqrt{74} (\pi - 0)\]\)
\(\[S = \sqrt{74}\pi\]\)
Therefore, the length of the curve described by the polar equation
\(\(r = 5\sin(\theta) + 7\cos(\theta)\) from \(\theta = 0\) to \(\theta = \pi\) is \(\sqrt{74}\pi\)\)
Confirming using the definite integral:
\($\[S = \int_{0}^{\pi} \sqrt{74} d\theta = \sqrt{74} [\theta]_{0}^{\pi} = \sqrt{74}(\pi - 0) = \sqrt{74}\pi\]\)
So, the length of the curve is indeed \(\(\sqrt{74}\pi\)\), which matches our earlier result.
To know more about length, visit:
https://brainly.com/question/30460787
#SPJ11
The projected year-end assets in a collection of trust funds, in trillions of dollars, where t represents the number of years since 2000, can be approximated by the following function where 0sts 50. A(t) = 0.00002841³ -0.00450² +0.0514t+1.89 a. Where is A(t) increasing? b. Where is A(t) decreasing? a. Identify the open intervals for 0sts 50 where A(t) is increasing. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. OA. The function is increasing on the interval(s) (Type your answer in interval notation. Round to the nearest tenth as needed. Use a comma to separate answers as needed.) OB. There are no intervals where the function is increasing.
Answers
The open interval where A(t) is increasing is (0.087, 41.288).
To find where A(t) is increasing, we need to examine the derivative of A(t) with respect to t. Taking the derivative of A(t), we get A'(t) = 0.00008523t² - 0.009t + 0.0514.
To determine where A(t) is increasing, we need to find the intervals where A'(t) > 0. This means the derivative is positive, indicating an increasing trend.
Solving the inequality A'(t) > 0, we find that A(t) is increasing when t is in the interval (approximately 0.087, 41.288).
Learn more about derivative here:
https://brainly.com/question/25324584
#SPJ11
Write the equation of the line that passes through the points (8, –1) and (2, –5) in standard form, given that the point-slope form is y + 1 = (x – 8).
Answers
Answer:
Ax + By = C is standard form.
y + 1 = (2/3)(x - 8)
distribute the (2/3)
y + 1 = (2/3)x - (16/3)
Multiply each term by 3 to clear the fractions.
3y + 3 = 2x - 16
Subtract 2x from both sides.
-2x + 3y + 3 = - 16
Subtract 3 from both sides.
-2x + 3y = - 19
Correct form typically has the leading coefficient as a positive number so multiply each term by - 1.
2x - 3y = 19
Step-by-step explanation:
Answer:
The answer is 2x + -3y = 19
Step-by-step explanation:
got it right on edge
What is the area of the triangle Please answer quick

Answers
Answer:
A = 25 in^2Step-by-step explanation:
\(area = \frac{1}{2} b \times h \\ area = \frac{1}{2} (10)(5) \\ area = 5 \times 5 \\ area = 25 \: {in}^{2} \)
I hope that is useful for you
The function y = 5.75 + 2.5(x - 2) can be used to determine cost in
dollars to rent a house of x square feet. What is the rate of change of
the cost in dollars with respect to the number of square feet?
Answers
The rate of change of the cost in dollars with respect to the number of square feet is; 2.5 dollars per square feet.
The function given, y = 5.75 + 2.5(x - 2) can be rewritten so as to resemble the equation of a straight line in slope-intercept form.
In essence, y = mx + cConsequently, the slope, m represents the rate of change of the cost in dollars with respect to the number of square feet.
The function y = 5.75 + 2.5(x - 2) on expansion then becomes;
y = 0.75 + 2.5xwhere, 2.5 is the slope and consequently, represents the rate of change of the cost in dollars with respect to the number of square feet.
Read more:
https://brainly.com/question/11884403
Alicia borrowed $3000 from a bike at a rate of 12% simple interest per year how much interest did she pay in four years
Answers
Answer:
$1440
Step-by-step explanation:
$3000 (12%) = 360
360 x 4 = 1440
Hope this helps!
2 (3)^3 + 5
And explain how you got it
Answers
Answer:
59
Step-by-step explanation:
3^3=27
2x27=54
27+54+5=59
Answer:
2 times 3 i 6 o 3 plus 5 equal 8
Step-by-step explanation:
beca you supoed to multiply ad divide
alg 1 adding/subtracting with rational expression

Answers
\(\qquad\qquad\huge\underline{{\sf Answer}}\)
Let's evaluate ~
As the denominator of both the terms is same, we can simply perform subtraction on numerator.
That is :
\(\qquad \sf \dashrightarrow \: \dfrac{a - 2}{ {a}^{2} + 7a + 6 } - \dfrac{5a - 6}{ {a}^{2} + 7a + 6 } \)
\(\qquad \sf \dashrightarrow \: \dfrac{a - 2 - (5a - 6)}{ {a}^{2} + 7a + 6 } \)
\(\qquad \sf \dashrightarrow \: \dfrac{a - 2 - 5a + 6}{ {a}^{2} + 7a + 6 } \)
\(\qquad \sf \dashrightarrow \: \dfrac{ - 4a + 4}{ {a}^{2} + 7a + 6 } \)
Answer:
-4a + 4/ a^2 + 7a +6
Find the slope of the line that goes through the points (9,-13) and (7,3).
Answers
hi
You have two points A ( X;Y) and B ( X ; Y)
slope is : ( Yb -Ya) / (Xb -Xa )
(3 - (-13) ) / ( 7 - 9) = (3 +13) / -2 = 16/-2 = - 16/2 = -8
slope is -8
Answer:
-8
Step-by-step explanation:
The slope formula is as follows:
m = y2 - y1 / x2 - x2
You would first plug in the points into the formula, and this is what you would get:
m = 3 - (-13) / 7 - 9
From there, because of additive inverse, the negative signs would become + signs.
m = 3 + 13 / 7 - 9
You would now add/subtract.
m = 16 / -2
And lastly, you would simplify.
m = 8/-1
8/-1 is the same thing as a slope of -8.
are the trigonometric functions odd, even, or neither odd nor even? select answers from the drop-down menus to correctly complete the statements. the function f(x)
Answers
The function f(x) is: neither old nor even
Trigonometric functions can be categorized as odd, even, or neither odd nor even based on their symmetry properties. Let's analyze each category:
Odd Functions: An odd function satisfies the condition f(-x) = -f(x) for all values of x. This means that if we reflect the graph of the function across the y-axis, it remains unchanged. In other words, the function is symmetric with respect to the origin (0,0).
Examples of odd trigonometric functions include sine (sin(x)) and tangent (tan(x)). When you plug in -x into these functions, you'll get the negation of the function's value at x.
Even Functions: An even function satisfies the condition f(-x) = f(x) for all values of x. This means that if we reflect the graph of the function across the y-axis, it remains unchanged. In other words, the function is symmetric with respect to the y-axis.
An example of an even trigonometric function is the cosine function (cos(x)). When you plug in -x into the cosine function, you'll get the same value as when you plug in x.
Neither Odd nor Even: Some trigonometric functions do not exhibit either odd or even symmetry. These functions do not satisfy the conditions for odd or even functions. Examples of trigonometric functions that are neither odd nor even include secant (sec(x)), cosecant (csc(x)), and cotangent (cot(x)). When you plug in -x into these functions, you won't get the negation or the same value as when you plug in x.
Therefore, the trigonometric functions can be categorized as odd, even, or neither odd nor even, depending on their symmetry properties.
Learn more about trigonometric function here, https://brainly.com/question/1143565
#SPJ11
Help pls. Solve the system of linear equations by substitution.

Answers
Answer:
(5, 3)
Step-by-step explanation:
\(x = 17 - 4y \\ y = x - 2\)
Substitute x into y:
\(y = (17 - 4y) - 2 \\ y = 15 - 4y \\ y + 4y = 15 \\ 5y = 15 \\ y = 3\)
Substitute y into x:
\(y = x - 2 \\ 3 = x - 2 \\ 3 + 2 = x \\ x = 5\)
Therefore your answer is (5, 3).
What postulate or theroem prove these triangles are congruent?

Answers
Answer:
The Answer To Your To Your Question Is SAS (Side-Angle-Side) Theroem
Answer:
Side angle side Theorem
Step-by-step explanation:
Find the product. (a2)(2a3)(a2 â€"" 8a 9) 2a7 â€"" 16a6 18a5 2a7 â€"" 16a6 â€"" 18a5 2a8 â€"" 16a7 18a6 2a12 â€"" 16a7 18a6
Answers
Suppose y varies inversely with x, and y = 49 when x = 17
. What is the value of x when y = 7 ?
Answers
Answer:
119 is the value of x when y = 7
Step-by-step explanation:
Since y varies inversely with x, we can use the following equation to model this:
y = k/x, where
k is the constant of proportionality.Step 1: Find k by plugging in values:
Before we can find the value of x when y = k, we'll first need to find k, the constant of proportionality. We can find k by plugging in 49 for y and 17 for x:
Plugging in the values in the inverse variation equation gives us:
49 = k/17
Solve for k by multiplying both sides by 17:
(49 = k / 17) * 17
833 = k
Thus, the constant of proportionality (k) is 833.
Step 2: Find x when y = k by plugging in 7 for y and 833 for k in the inverse variation equation:
Plugging in the values in the inverse variation gives us:
7 = 833/x
Multiplying both sides by x gives us:
(7 = 833/x) * x
7x = 833
Dividing both sides by 7 gives us:
(7x = 833) / 7
x = 119
Thus, 119 is the value of x when y = 7.
Jaylin solved this equation from the card sort:
15 – 7x= 3 + 5x
12 – 7x= 5x
12 = 12x
1= x
Is this correct?
Answers
Find the measure.
m \angle 5
Answers
The measurement of angle 5 is 101 degrees. This result is obtained by applying the properties of parallel lines and corresponding angles, as well as the fact that angles on a straight line add up to 180 degrees.
In the given figure, we have two parallel lines intersected by a transversal. When two parallel lines are cut by a transversal, the corresponding angles are congruent. Therefore, angle 6 is equal to 79 degrees.
Since angle 5 and angle 6 are situated on the same line, they form a linear pair, which means their sum is 180 degrees. By substituting the value of angle 6 as 79 degrees into the equation, we can solve for angle 5:
angle 5 + 79 degrees = 180 degrees
Subtracting 79 degrees from both sides, we get:
angle 5 = 180 degrees - 79 degrees
Simplifying, we find:
angle 5 = 101 degrees
Thus, the measurement of angle 5 is 101 degrees. This result is obtained by applying the properties of parallel lines and corresponding angles, as well as the fact that angles on a straight line add up to 180 degrees.
To know more about angle:
https://brainly.com/question/29588076
#SPJ4

After carrying out the operations below, what is the correct answer using the correct number of significant figures in the result? 13.7+0.027+8.221 21.921 22 21.9 21.92
Answers
The correct answer using the correct number of significant figures is 21.9.
To determine the correct answer with the appropriate number of significant figures, we need to consider the rules for significant figures.cThe result should be rounded to the fewest number of decimal places in any of the supplied integers whether adding or subtracting numbers.
In this case, the numbers being added have varying decimal places. 13.7 has one decimal place, 0.027 has three decimal places, and 8.221 has three decimal places.
To add these numbers, we align the decimal points and sum the values: 13.7 + 0.027 + 8.221 ------- 21.948
To follow the rule for significant figures, the least number of decimal places is one (from 13.7).
Therefore, the answer should be rounded to one decimal place.
Hence, the correct answer using the correct number of significant figures is 21.9.
Learn more about decimal at
https://brainly.com/question/30958821
#SPJ11
PART 1
John is saving money to buy a car. He takes $8,000 to the bank and opens an annual CD upon which the bank agrees to pay him 2% interest.
Principal = 8000
Term = 1 year
APR = 2% = 0.02
8000 x 0.02 = $160
8000 + 160 = $8,160
Beginning Balance
2% Interest
Ending Balance
$8,000.00
$160
$8,160
After one year, Michael earned $160 in interest on his initial deposit of $8,000, so his balance is now $8,160.
Calculate the Annual interest below (first image):
PART B:
Now, let’s say John leaves his money in the bank for four years. The term of the annual CD is four years, so he will be earning 2% interest per year for four years. Since this is an annual CD, interest will be added to the principal at the end of every year. This is called annual compounding. Complete the following table (2nd Image), filling in the cells for years 5 through 10.


Answers
John will earn an annual interest of $500 on a beginning balance of $10,000 at a rate of 5% per year. After one year, the ending balance will be $10,500. John earned $160 in interest after leaving his initial deposit of $8,000 in the bank for first year with annual compounding at a 2% interest rate. His ending balance was $8,160. The table shows his ending balance for years 5-10.
We can use the formula for simple interest to calculate the annual interest earned by John on a balance of $10,000 at a rate of 5% per year
Annual interest = (Principal x Rate x Time) / 100
where Principal is the beginning balance, Rate is the interest rate, and Time is the duration of investment in years.
Substituting the given values, we get
Annual interest = (10000 x 5 x 1) / 100 = $500
Therefore, the annual interest earned by John on a balance of $10,000 at a rate of 5% per year is $500.
Ending balance after one year = Beginning balance + Annual interest = $10,000 + $500 = $10,500.
since the term of the annual CD is four years, and John will leave his money in the bank for four years, we can calculate the ending balance at the end of each year using the formula above.
For year 5
P = $8,160
r = 0.02
n = 1
t = 1
A = $8,160 (1 + 0.02/1)^(1x1) = $8,324.80
For year 6
P = $8,324.80
r = 0.02
n = 1
t = 1
A = $8,324.80 (1 + 0.02/1)^(1x1) = $8,492.78
For year 7
P = $8,492.78
r = 0.02
n = 1
t = 1
A = $8,492.78 (1 + 0.02/1)^(1x1) = $8,664.28
For year 8
P = $8,664.28
r = 0.02
n = 1
t = 1
A = $8,664.28 (1 + 0.02/1)^(1x1) = $8,839.44
For year 9
P = $8,839.44
r = 0.02
n = 1
t = 1
A = $8,839.44 (1 + 0.02/1)^(1x1) = $9,018.34
For year 10
P = $9,018.34
r = 0.02
n = 1
t = 1
A = $9,018.34 (1 + 0.02/1)^(1x1) = $9,201.05
Therefore, the table for years 5 through 10 would look like
To know more about Annual interest:
https://brainly.com/question/30573341
#SPJ1

solve: x + 1 < 5
Me confused and need help
Answers
Answer: x < 4
Step-by-step explanation: You are trying to isolate the variable, x, so you have to subtract 1 on both sides of the inequality. Then, you are left with x < 4.