A survey of 7th and 8th grade students asked whether they were in favor of or against school uniforms. The two-way table below shows the results. To the nearest tenth of a percent, what percent of the 7th Grade students were in favor of wearing school uniforms
Answers
The percent of the 7th graders that are in favor of school uniforms is 42.857% which can be rounded as 42.9%.
The survey results show there are a total of 112 7th-grade students and from this total, the number of students that support school uniforms is 48.
Let's calculate the percentage 48 represents:
100% = 112x = 48x = 48 x 100 / 112 x = 4800 / 112x = 42. 857This means the percentage of 7th graders that support uniforms is 42.857% which can be rounded to
Learn more about percentage in: https://brainly.com/question/834969

Related Questions
If the variance of a probability was computed to be \( 4.8 \) grams, what is the standard deviation? a \( \quad 1.9 \) b \( \quad 2.2 \) c \( \quad 1.6 \) d \( \quad 0.6 \)
Answers
If the variance of a probability distribution is computed to be 4.8 grams, the standard deviation would be approximately 2.2 grams.
The standard deviation is the square root of the variance. In this case, the given variance is 4.8 grams. To find the standard deviation, we take the square root of the variance.
Using the formula, we have standard deviation = √variance. Plugging in the value of the variance, we get standard deviation = √4.8 ≈ 2.2 grams.
Therefore, the standard deviation of the probability distribution is approximately 2.2 grams, which corresponds to option b.
Learn more about variance here:
https://brainly.com/question/14116780
#SPJ11
4 + {−5 + [−3 + 4 + 2(−7 + 4) + 4] + 2}
7 + {−2 + [5 + 4(−3) + (−6 + 2) + (−3)]}
(−2) + {3 + [−4 + (3)] + 7} + (−5)
(−10) + {−7 + [−4 + 5(−9) + 5] + 8}
18 + 3{−4 + [−15 + 20 + (−3)] + (−9)}
−(−8 + 5) + {−4 + [−7 + (−9 − 5) + 3]}
− 9 + {−7 − 2[−(4 + 1) + (5 − 9)]} − 3
−1 − 3{6 − [4 + 2(−7 + 8) − 5] − 2}
−(−2) − {−(−7) + [−3 + (−5 − 2) + 6]}
−(−6 − 2) − 2{−4(−5) + 5[−3 + (−2)]}
6 − 2{−4 + 3[3 − 3(−8 − 5) + 14] − 7}
Me pueden ayudar por favor es urgente!!! y Buenas Noches ;)
Answers
Answer
it is 5 : )
Step-by-step explanation:
Given the following segment lengths find a length of the segment
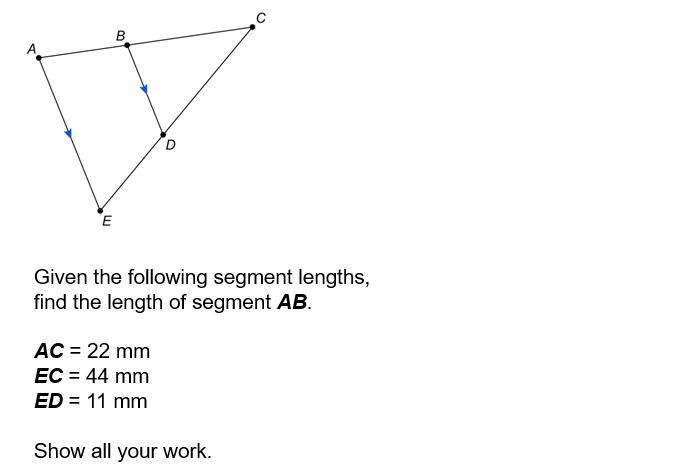
Answers
The length of the line segment AB is 11/2 mm.
What is a triangle?A triangle is a three-sided closed-plane figure formed by joining three noncolinear points.
Based on the side property triangles are of three types they are Equilateral triangle, Scalene triangle, and Isosceles triangle.
We know a line segment parallel to one side of a triangle divides the other two sides in the same ratio.
Therefore, AC/AB = EC/ED.
22/AB = 44/11.
2/AB = 4/11.
4AB = 22.
AB = 11/2.
learn more about triangles here :
https://brainly.com/question/14653505
#SPJ1
Find the final price after a discount of 15% and then a sales tax of 4.67%
a) a PlayStation 5 for 750
b) 3 pairs of Yeezys for 265
Answers
Solution: (a)
15% of 750 is 112.5 750-112.5=637.5 4.67% of 637.5 is 29.7712 637.5 + 29.7712 = 667. 27125
oncepts
What is the average of 4.2, 2.61, and 3.6?
Answers
Answer:
hope it helps
Step-by-step explanation:
answer is 3.47
4.2+2.61+3.6=10.41
10.41÷3=3.47
Security x has expected return of 9% and standard deviation of 18%. Security y has expected return of 12% and standard deviation of 21%. If the two securities have a correlation coefficient of 0. 4, what is their covariance?.
Answers
Their covariance is -0.0151
Given;
The expected return on security x is 9%, whereas the standard deviation is 18%. The expected return on security y is 12%, and the standard deviation is 21%. If the correlation between the two securities is 0.4
Security X:
Expected return E(Rx) = 9% = 0.09
Standard deviation (σx) = 18% = 0.18
Security Y:
Expected return E(Ry) = 12% = 0.12
Standard deviation (σy) = 21% = 0.21
and
Corr(X,Y) = -0.4
We know that,
Corr(X,Y) = Cov(X,Y)/ σx*σy
Substituting the above-given values, we get;
-0.4 = Cov(X,Y)/ 0.18*0.21
-0.4 = Cov(X,Y)/ 0.0378
Cov(X,Y) = -0.4*0.0378
Cov(X,Y) = -0.0151
Therefore, the covariance is -0.0151.
To learn more about covariance click here:
brainly.com/question/17137919
#SPJ4
Multiply (x-4)².
Please help me
Answers
⇒ x-4 is the term in this case there for the term (x-4) is squared meaning the term has to multiply itself twice.
\(=(x-4)(x-4)\\=x(x-4)-4(x-4)\\=x^{2} -4x-4x+16\\=x^{2} -8x+16\)
If you are still struggling on how to multiply out DM ASAP.
Extrema
The maximum height of the tennis ball is 3 feet higher during th
shot.
Answers
The height that the tennis ball attains from the ground while executing the present stroke is up to 34 feet.
How to solveAssuming the tennis ball reached a peak height of 25 feet in the previous shot, it is now expected to reach a peak height of 28 feet in the current shot as it has climbed an additional 3 feet from the previous peak.
Given that the tennis ball was launched from a height of six feet, its maximum elevation above the ground can be calculated by adding the height of its ascent, which is 28 feet, resulting in a total of 34 feet.
Thus, the height that the tennis ball attains from the ground while executing the present stroke is up to 34 feet.
Read more about maximum height here:
https://brainly.com/question/12446886
#SPJ1
The Complete Question
A tennis ball is shot straight up into the air from a height of 6 feet. If the maximum height it reaches during this shot is 3 feet higher than the previous shot, and the maximum height during the previous shot was 25 feet, what is the final maximum height of the tennis ball during the current shot?
(1)/(4p)(x-h)^(2)+k=0
Multiply the equation by 4p. Explain how different values of k affect the number of zeros of the polynomial. Consider k > 0, k = 0, and k < 0. Assume p > 0.
Answers
Answer:
Step-by-step explanation:
Given p>0, multiply the equation by 4p: (1/4p)*(x-h)^(2)+k=0
(x-h)^2+4kp = 0
k>0
4kp>0
(x-h)^2 = -4kp
So x has imaginary roots only. There is no real zeros of the polynomial.
k=0
4kp=0
(x-h)^2 = 0
x=h
So x has one real root and the polynomial has one zero
k<0
4kp<0
(x-h)^2 = -4kp
So x has two real roots and the polynomial has two real zeros.
Answer:
Step-by-step explanation:
Assume that and multiply the equation by 4p. Then you obtain the equation (x-h)^2+4pk=0.
1) If k>0, then 4pk>0 and the equation does not have real solutions and there is no zero.
2) If k=0, then 4pk=0 and . There is one solution x=h and there is one zero.
2) If k<0, then 4pk<0 and the equation has two different solutions and there are two zeros.
If ABC ~ AMN and AM = 6, MB = 4, AN = 8, then what is
the value of NC?

Answers
According to the question, the information provided makes it impossible to assess the value of NC?
Describe the tetrahedron.Tetrahedrons, also called triangle pyramids, are polyhedra with four trapezoidal faces, six edges that are level, and four vertex corners. The tetrahedron, which additionally happens to be the most straightforward of them all, is the only regular symmetric polygon with lower than five faces. The cylindrical structure at the base of the triangle is made of tetrahedra. If an object has four triangular-shaped faces, it is a tetrahedron. Regular Tetrahedrons are the ones that have equilateral triangle bases and isosceles triangle faces. A polyhedron has four sides.
Two comparable triangles, and ABC and AMN, are present in the given issue, because where "" indicates similarity.
The details are as follows:
AN = 8 AM = 6 MB = 4
We receive a request to determine NC's value.
The ratios of related sides are identical in similar triangles, which have proportionate sides. Using the equivalent ends of ABC and AMN, we can establish a ratio:
NC/AN = AB/AM
replacing the specified values:
AB/6 = NC/8
We can traverse-multiply and then use that result to solve for NC:
8 x AB 6 x NC 8 x AB 6 x NC
(Simplifying by dividing the two sides by 2) NC = (8AB)/6 NC = (4AB)/3
Since we do not have a specific value for AB or any additional information about the triangles, we cannot determine the exact value of NC. We can only express it in terms of AB, which is not provided in the given problem. Therefore, the value of NC cannot be determined with the information given.
To know more about tetrahedron visit:
https://brainly.com/question/17132878
#SPJ1
Es.
3
e
5. Andrew says that 60 is the greatest whole
number that rounds to 60. Is Andrew
correct? Explain your reasoning
Answers
Andrew is correct because 60 is the highest whole number that can round to 60. Any number higher than 60 will round up to a higher number. For example, 61 will round up to 70, and 62 will round up to 70. Therefore, 60 is the greatest whole number that rounds to 60.
The highest whole number is infinity, as there is no limit to how high a number can be. Whole numbers are all the numbers that are greater than or equal to 0, including 0 itself. The highest whole number is therefore infinity, as this is the highest possible number.
Learn more about the greatest whole number:
https://brainly.com/question/593507
#SPJ4

Use (8), ∫ t 0 f(τ) dτ = = ℒ−1 {F(s)/s}, to evaluate the given inverse transform. (Write your answer as a function of t.)
ℒ−1 {1/s^3(s − 1)}
Answers
Using the formula ∫ t 0 f(τ) dτ = ℒ−1 {F(s)/s}, we have:
∫ t 0 (1/τ^3) (1/(s-1)) ds
= ∫ t 0 (1/τ^3) (1/(s-1)) ds
= [(-1/2) (1/τ^3) e^(s-1)]_0^t
= (-1/2) [(1/t^3) e^(t-1) - (1/0^3) e^(0-1)]
= (-1/2) [(1/t^3) e^(t-1) - e^(-1)]
Therefore, the inverse Laplace transform of 1/s^3(s-1) is:
ℒ−1 {1/s^3(s-1)} = (-1/2) [(1/t^3) e^(t-1) - e^(-1)]
To evaluate the given inverse Laplace transform, ℒ^−1{1/s^3(s − 1)}, we can use the property (8), which states that ∫ t 0 f(τ) dτ = ℒ^−1{F(s)/s}. In this case, F(s) = 1/s^2(s - 1).
First, perform partial fraction decomposition on F(s):
1/s^2(s - 1) = A/s + B/s^2 + C/(s - 1)
Multiplying both sides by s^2(s - 1) to eliminate the denominators:
1 = A(s^2)(s - 1) + B(s)(s - 1) + Cs^2
Now, we will find the values of A, B, and C:
1. Setting s = 0: 1 = -A => A = -1
2. Setting s = 1: 1 = C => C = 1
3. Differentiating the equation with respect to s and setting s = 0:
0 = 2As + Bs - B + 2Cs
0 = -B => B = 0
Now we can rewrite F(s) using the values of A, B, and C:
F(s) = -1/s + 0/s^2 + 1/(s - 1)
Next, we can find the inverse Laplace transform of each term separately:
ℒ^−1{-1/s} = -1
ℒ^−1{0/s^2} = 0
ℒ^−1{1/(s - 1)} = e^t
Finally, combine these results and multiply by the unit step function u(t) to obtain the final answer:
f(t) = (-1 + 0 + e^t)u(t) = (e^t - 1)u(t)
Visit here to learn more about denominators : https://brainly.com/question/7067665
#SPJ11
If x = 11 , evaluate the following expression: x + 4
Answers
Answer:
Substitute x = 11 to x + 4, you get,
11 + 4 = 15
Thanks
\(x+4\) when x is equal to 11
Evaluate:
\((11)+4\)
\(=15\)
classify -t+4 and state its degree
Answers
Answer:
yes same
Step-by-step explanation:
Write a differential formula that estimates the change in volume of a sphere when the radius changes from
Answers
Answer:
d.
took the test
Step-by-step explanation:
describe how 20,000 and 2,000 related
Answers
Answer:
They both have 3 zero's both have the number 2
They both are numbers
a morning​ consult/politico poll of registered voters in july 2020 asked a standard polling question of whether the united states was headed in the​ right direction or was on the​ wrong track. ​% said that things are on the wrong track vs. ​% who said​ right direction. complete parts a and b.a) Calculate the margin of error for the proportion of all U.S. adults who think things are on the wrong track for 95% confidence. ME= 0.019 (Round to three decimal places as needed.) b) Explain what this margin of error means. Select the correct choice below and fill in the answer box within your choice. (Round to three decimal places as needed.) A. The probability that any given adult surveyed from the sample responded "Wrong Track" is____. B. One is 95% confident that the observed proportion of adults that responded "Wrong Track" is within___of the population proportion.C. One is 95% confident that the observed proportion of adults that responded "Wrong Track" is within_____of the sample proportion.D. The probability that any given adult surveyed from the population will respond "Wrong Track" is_____.
Answers
a) Margine of error for the proportion of all U.S. adults who think things are on the wrong track for 95% confidence is 0.019.
b) Correct answer is B. One is 95% confident that the observed proportion of adults that responded "Wrong Track" is within ±0.019 of the population proportion.
How to calculate the margin of error and assess the correct option?a) To calculate the margin of error for the proportion of all U.S. adults who think things are on the wrong track for 95% confidence, we can use the following formula:
ME = z√((p(1-p))/n)
Where:
z = the z-score associated with the desired level of confidence (in this case, 1.96 for 95% confidence)
p = the proportion of adults in the sample who said things are on the wrong track
n = the sample size
Using the percentages provided in the question, we can calculate the sample proportion:
p = % of adults who said things are on the wrong track / 100
p = % / 100 = %
So, p =
We don't have the sample size, but we can assume it's large enough (at least 30) to use the normal distribution approximation. Therefore, we can use the percentages directly to calculate the margin of error:
ME = 1.96√((0.490.51)/n)
ME = 1.96√(0.2499/n)
ME = 1.96(0.499/n¹/²)
ME = 0.019
Hence the margine of error is 0.019.
b) The margin of error means that if we were to conduct the same survey many times and calculate a 95% confidence interval for the proportion of all U.S. adults who think things are on the wrong track using each sample, we would expect the true population proportion to be within ±0.019 of the sample proportion in 95% of the intervals.
Therefore, the correct answer is B. One is 95% confident that the observed proportion of adults that responded "Wrong Track" is within ±0.019 of the population proportion.
Learn more about Margine of error.
brainly.com/question/29101642
#SPJ11
Glen mixes red bricks with yellow bricks when building sides of a brick house. The ratio is 3 pieces of red brick for every 7 pieces of yellow brick. If there are 28 pieces of yellow brick, how many pieces of red brick will there be?
Answers
Answer:
12 red bricks
Step-by-step explanation:
A potential is V(x,z) = 4bx^2+4az^3-3cz^3. Find E field
= 0. A b and c are positive
Answers
The electric field (E-field) associated with the given potential function V(x, z) = 4bx^2 + 4az^3 - 3cz^3 is E = -8bx i - (12az^2 - 9cz^2)j.
To find the electric field (E-field) associated with the given potential function, we need to calculate the negative gradient of the potential. The E-field is given by the following formula:
E = -∇V
Where ∇ is the gradient operator. In this case, the potential function V(x, z) is defined as:
V(x, z) = 4bx^2 + 4az^3 - 3cz^3
To calculate the E-field, we need to take the partial derivatives of V with respect to x and z and then apply the negative sign. Let's calculate each component separately:
Partial derivative with respect to x (dV/dx):
dV/dx = 8bx
Partial derivative with respect to z (dV/dz):
dV/dz = 12az^2 - 9cz^2
Now, we can write the E-field vector as:
E = -∇V = -(dV/dx)i - (dV/dz)j
Substituting the calculated partial derivatives, we have:
E = -8bx i - (12az^2 - 9cz^2)j
Therefore, the electric field (E-field) associated with the given potential function V(x, z) = 4bx^2 + 4az^3 - 3cz^3 is:
E = -8bx i - (12az^2 - 9cz^2)j
Note that the positive constants b and c are included in the E-field expression.
Learn more about electric field here
https://brainly.com/question/19878202
#SPJ11
A brown bear can run 44 meters in 4 seconds. At this rate, how far could a brown bear run in 20 seconds?
Answers
Answer:
220 meters
Step-by-step explanation:
20 seconds is 5 times larger than 4 seconds, so the distance it runs in 20 seconds should be 5 times longer than 44 meters
so:
20/4 = 5
since x is 5 times larger than 44, set up the equation
5 = x/44
multiply both sides by 44
x= 44 * 5 = 220 meters
Please help, it’s due tomorrow

Answers
Answer:
The largest interger that satisfies the equation is 3
Step-by-step explanation:
If we subtract 10 from each side, we get 7x<=21
Then, we divide 7 on each side to get x<=3.
So the largest interger to satisfy the equation is 3
(Btw, <= means less than or equal to)
Hope this helped you, and have a great day!
Answer:
x<=3
Step-by-step explanation:
minus 10 fom both sides
7x + 10-10<=31-10
restate as
7x<=21
divid both side by same factor
7x/7 and 21/7
restate as
x<=3
Can somebody help me please

Answers
Answer:
x = 5
Step-by-step explanation:
The inner and outer triangles are similar by the AA postulate then the ratios of corresponding sides are in proportion, that is
\(\frac{x}{2}\) = \(\frac{6+4}{4}\) = \(\frac{10}{4}\) = 2.5 ( multiply both sides by 2 to clear the fraction )
x = 5
Moon Software Inc. is planning to issue two types of 25-year, noncallable bonds to raise a total of $6 million, $3 million from each type of bond. First, 3,000 bonds with a 10% semiannual coupon will be sold at their $1,000 par value to raise $3,000,000. These are called "par" bonds. Second, Original Issue Discount (OID) bonds, also with a 25 -year maturity and a $1,000 par value, will be sold, but these bonds will have a semiannual coupon of only 7.75%. The OID bonds must be offered at below par in order to provide investors with the same effective yield as the par bonds. How many OID bonds must the firm issue to raise $3,000,000 ? Disregard flotation costs, and round your final answer up to a whole number of bonds.
3,776
3,096
3,927
2,870
4,456
Answers
Moon Software Inc. must issue approximately 3,927 OID bonds to raise $3,000,000.
The par bonds have a coupon rate of 10% and a par value of $1,000. To raise $3,000,000, Moon Software Inc. needs to issue 3,000 par bonds since $3,000,000 divided by $1,000 equals 3,000.
The OID bonds have a semiannual coupon rate of 7.75% and a par value of $1,000. Since these bonds need to provide investors with the same effective yield as the par bonds, they must be offered at a discount. To calculate the number of OID bonds required, we need to determine the discount needed to match the effective yield of the par bonds.
The effective yield of the par bonds is 10%. The OID bonds have a coupon rate of 7.75%, so the discount needed to match the effective yield is 10% - 7.75% = 2.25%.
To raise $3,000,000 with OID bonds, we divide the amount by the discount rate: $3,000,000 / 2.25% = $133,333,333.33.
Since each OID bond has a par value of $1,000, we divide the total amount by $1,000: $133,333,333.33 / $1,000 = approximately 133,333.33 bonds.
Since we need a whole number of bonds, we round up to the nearest whole number, which gives us 133,334 bonds.
Therefore, Moon Software Inc. must issue approximately 133,334 OID bonds to raise $3,000,000.
Learn more about approximately here:
https://brainly.com/question/31695967
#SPJ11
Which of the following results in the expression 0.22 x 86?
22 of 86%
22% of 86
86% of 0.22
0.86 of 22%
oH saVe mE sisTerS
Answers
Answer:
22% of 86
Step-by-step explanation:
22% = 0.22
0.22 × 86
Write an equation in point-slope form for the line that satisfies the given set of conditions.
slope of 4/5, passes through (10,-3)
Answers
Answer:
y + 3 = \(\frac{4}{5}\) (x - 10)
Step-by-step explanation:
The equation of a line in point- slope form is
y - b = m(x - a)
where m is the slope and (a, b ) a point on the line
Here m = \(\frac{4}{5}\) and (a, b ) = (10, - 3 ) , then
y - (- 3) = \(\frac{4}{5}\) (x - 10) , that is
y + 3 = \(\frac{4}{5}\) (x - 10)
work out the average speed of 40 km in 2.5 hours
Answers
Answer:
19.20
Step-by-step explanation: used
a calc
For the function y = 3 cos(4x − 2 ) + 5, state the amplitude,
period, the specific phase shift, and the specific vertical
shift.
Answers
Rounding to two decimal places, the approximate distance from the object to the point on the ground is 103.46 meters.
Let's call the point where the surveyor is standing point A and the object on the ground point B. We can draw a right triangle ABC where:
A is the top vertex of the triangle
B is the bottom vertex of the triangle
C is the point directly below A on the ground
AB is the line of sight from the surveyor to the object
BC is the height of the surveyor above point C
We know that angle BAC is (90^{\circ}) since AB is the line of sight and AC is perpendicular to the ground. We also know that angle BCA is (67^{\circ}) since it is the angle of depression of the object from the surveyor.
Using trigonometry, we can find the length of AB as follows:
[\tan 67^{\circ} = \frac{AB}{BC}]
Solving for AB, we get:
[AB = BC \cdot \tan 67^{\circ}]
We know that BC is equal to the height of the surveyor above the ground, which is 35 meters. Therefore:
[AB = 35 \cdot \tan 67^{\circ} \approx 103.46]
Rounding to two decimal places, the approximate distance from the object to the point on the ground is 103.46 meters.
Learn more about distance from
https://brainly.com/question/30395212
#SPJ11
Can the sides of a triangle have lengths 8, 11, and 17?
Answers
Answer:
Yes and no (YES: can be a triangle, but NOT a right angle triangle)
Step-by-step explanation:
Notice 8^2+11^2=185
while 17^2=289
Notice Pythagoras do apply for every right triangle. since 185 is not 289. is not a right triangle. But it can be a triangle (just not a right angle triangle)
Help please I’ll put you as brainliest

Answers
Answer:
the first one
Step-by-step explanation:
Nora learned a total of 4 appetizer recipes over the course of 2 weeks of culinary school.
After 6 weeks of culinary school, how many total appetizer recipes will Nora know? Solve
using unit rates.
appetizer recipes
Submit
Answers
Answer:
Nora will have learned 12 recipes over the course of 6 weeks at culinary school.
Step-by-step explanation:
In the question, we get the information that Nora learned 4 appetizers in the span of 2 weeks. Therefore, we divide 4 by 2 to learn how many she learned over the course of 1 week. We find that 4/2 = 2. Then, 2*6= 12.