A student was asked to find the slant height of a square pyramid if the length of each side of the base is 34 cm and the height is 25 cm. He incorrectly said the slant height is 7.7 cm. Find the slant height of the pyramid. What mistake might the student have made?
Answers
The slant height of the pyramid is 30.23 cm.
We have,
Height = 25 cm
Each side of base = 34 cm
So, The formula for slant height is given by,
s = √h² + (a/2)²
s= √25² + (34/2)²
s= √ 625 + 289
s= √914
s= 30.23 cm
Thus, the slant height is 30.23 cm
Learn more about slant height here:
https://brainly.com/question/31450059
#SPJ1
Related Questions
Which functions is nonlinear
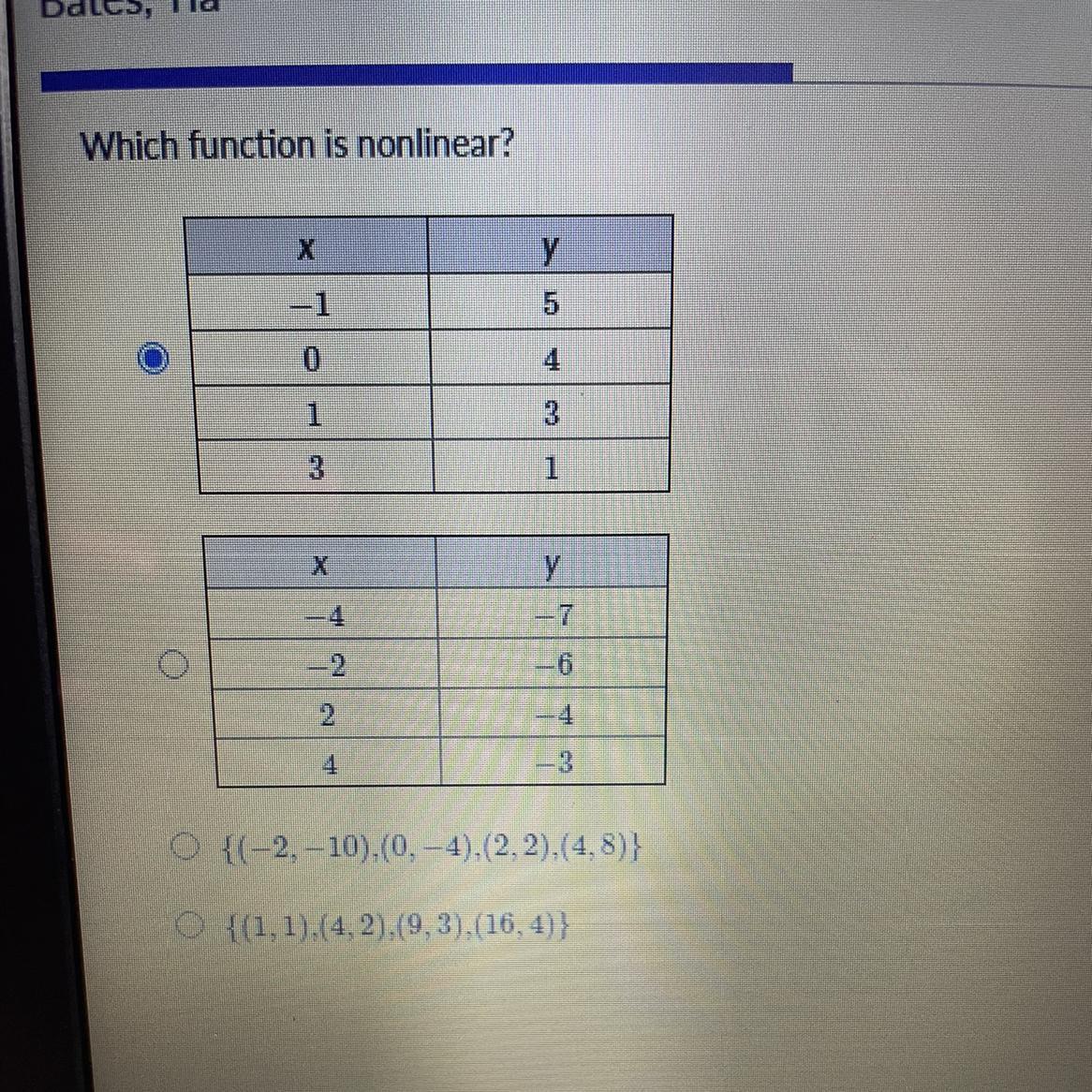
Answers
Answer:
the 3rd one
Step-by-step explanation:
Answer:
last one
Step-by-step explanation:
It took Melanie ⅓ of an hour to ride her bike 2¾ of a mile. How many miles per hour can Melanie ride her bike?
Answers
Answer:
8.25 or 8 \(\frac{1}{4} \\\)
Step-by-step explanation:
Find the roots and the vertex of the quadratic on a calculator. Round all values to 3 decimal places (if necessary).
�
=
20
�
2
+
180
�
−
567
y=20x
2
+180x−567
Answers
Answer:
Step-by-step explanation:
The quadratic equation is given as:
```
y = 20x^2 + 180x - 567
```
To find the roots of the quadratic, we can use the quadratic formula:
```
x = (-b ± √(b^2 - 4ac)) / 2a
```
In this case, the coefficients are:
```
a = 20
b = 180
c = -567
```
Substituting these values into the quadratic formula, we get:
```
x = (-180 ± √(180^2 - 4 * 20 * -567)) / 2 * 20
```
```
x = (-180 ± √(32400 + 42680)) / 40
```
```
x = (-180 ± √75080) / 40
```
```
x = (-180 ± 274.16) / 40
```
```
x = -4.25, -14.25
```
Therefore, the roots of the quadratic are -4.25 and -14.25.
To find the vertex of the quadratic, we can use the formula:
```
(-b / 2a, (4ac - b^2) / 4a)
```
In this case, the vertex is:
```
(-180 / 2 * 20, (4 * 20 * -567 - 180^2) / 4 * 20)
```
```
(-4.5, -79.75)
```
Therefore, the vertex of the quadratic is at (-4.5, -79.75).
The roots and the vertex of the quadratic are rounded to 3 decimal places.
What is the equation of the line that passes through the points (-2,10) and (-9,-5)? Write your answer in slope intercept form
Answers
\((\stackrel{x_1}{-2}~,~\stackrel{y_1}{10})\qquad (\stackrel{x_2}{-9}~,~\stackrel{y_2}{-5}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-5}-\stackrel{y1}{10}}}{\underset{run} {\underset{x_2}{-9}-\underset{x_1}{(-2)}}} \implies \cfrac{-15}{-9 +2} \implies \cfrac{ -15 }{ -7 } \implies \cfrac{ 15 }{ 7 }\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{10}=\stackrel{m}{ \cfrac{ 15 }{ 7 }}(x-\stackrel{x_1}{(-2)}) \implies y -10 = \cfrac{ 15 }{ 7 } ( x +2) \\\\\\ y-10=\cfrac{ 15 }{ 7 }x+\cfrac{ 30 }{ 7 }\implies y=\cfrac{ 15 }{ 7 }x+\cfrac{ 30 }{ 7 }+10\implies {\Large \begin{array}{llll} y=\cfrac{ 15 }{ 7 }x+\cfrac{100}{7} \end{array}}\)
Multiply.
Your answer should be a monomial in standard form.
(-3m5)(–2m4) =
Answers
The monomial \((-3m^5)(–2m^4)\)in standard form is \(6m^9\)
What is Algebraic expression ?
Algebraic expression can be defined as combination of variables and constants. An algebraic expression is a combination of variables, constants, and mathematical operations, such as addition, subtraction, multiplication, division, and exponentiation.
The variables represent unknown or unspecified values that can take on different numerical values, while the constants are specific, fixed values that do not change.
The mathematical operations are used to manipulate the variables and constants and to create different algebraic expressions.
Given expression ,
\((-3m^5)(–2m^4)\)
we know that \(a^m * a ^n = a ^ (m+n)\)
\((-3m^5)(-2m^4) = 6m^(5+4)\)
= \(6m^9\)
Therefore, the answer is \(6m^9\) in standard form.
To learn more about Algebraic expression from given link.
brainly.com/question/28884894
#SPJ1
How can you use properties of operations to expand expressions? QUICK PLEASE!!!!!!!!!!!!!!!!!
Answers
Step-by-step explanation:
hope it helps you
thank you

How do I isolate the y variable?
\(x = \frac{2y + 4}{3} \)
Answers
Answer:
y = \(\frac{3x}{2}\) - 4
Step-by-step explanation:
first multiply by 3 on both sides
then subtract 4 on both sides
finally you have to divide by 2 on both sides to get
y = \(\frac{3x}{2}\) - 4
13.- La factorización correcta d
expresión 3x2- 24x + 21 es:
A) (3x-3)(x+7)
B) (3x+21)(x-1)
C) (3x+1)(x+21)
D) (3x-3)(x-7)
reción y
Answers
Answer:
Option (D)
Step-by-step explanation:
The given expression is,
3x² - 24x + 21
We will factorize the given expression by the following steps,
3x² - 24x + 21
= 3(x² - 8x + 7)
= 3(x² - 7x - x + 7)
= 3[x(x - 7) - 1(x - 7)]
= 3(x - 1)(x - 7)
= (3x - 3)(x - 7)
Therefore, factored form of the given expression is (3x - 3)(x - 7).
Option (D) will be the correct option.
Mr. Smith is ordering steaks to serve at a poker game with his friends. The first company charges a delivery fee of $10 plus $15 per steak. The second company charges a delivery fee of $25 and charges $10 per steak. How many steaks would Mr. Smith have to order so that both companies cost the same amount?
Answers
Answer:
3
Step-by-step explanation:
1. One= $25 Two= $40 Three= $55
2. One= $35 Two= $45 Three= $55
A jewelry maker has 51 inches of chain. She wants to cut the chain into 9 equal parts. How long will each part be?
Answers
Answer:
7 that's the answer seven
4 Find a basis for the kernel of A (or, equivalently, for the linear transformation T(x) = Ar). A basis for the kernel of A is (1 point) Let A=
Answers
A basis for the kernel of A is { [2,-1,0,0], [1,0,1,0], [-3,0,0,1] }. To find a basis for the kernel of A, we need to find all solutions to the equation Ax = 0.
This can be done by row reducing the augmented matrix [A|0]:
[A|0] =
[ 1 -2 -1 3|0]
[ 2 -5 -1 6|0]
[-1 2 0 -3|0]
Row reducing this matrix gives:
[ 1 -2 -1 3|0]
[ 0 1 1 0|0]
[ 0 0 0 0|0]
So the system is equivalent to the equations x1 - 2x2 - x3 + 3x4 = 0 and x2 + x3 = 0. Solving for the basic variables in terms of the free variables, we get x1 = 2x2 + x3 - 3x4 and x2 = -x3. So the general solution is:
x = [2x2 + x3 - 3x4, -x3, x3, x4]
= x2[2,-1,0,0] + x3[1,0,1,0] + x4[-3,0,0,1]
Thus, a basis for the kernel of A is { [2,-1,0,0], [1,0,1,0], [-3,0,0,1] }.
Learn more about kernel here:
https://brainly.com/question/15183580
#SPJ11
Holly needs to buy some cloth to make masks. The following deals are available at various stores. Choose the best deal
A.
$11.04 per 4 yd
B.
$16.26 per 6 yd
C.
$19.11 per 7 yd
D.
$13.85 per 5 yd
Answers
Answer: B, $16.26 per 6 yards
Step-by-step explanation:
$11.04/ 4 yd is $2.76 a yd
$16.26/ 6 yd is $2.71 a yd
$19.11/ 7 yd is $2.73 a yd
$13.85/ 5 yd is $2.77 a yd
Check the image for the question.

Answers
The mathematical model that best fits the given data is option : y = 82.3 - 8.275x.
To construct a scatterplot and determine the mathematical model that best fits the given data, we will plot the points and analyze the trend.
Given Data:
x: 4, 8, 12, 16, 20
y: 40, 20, -11, -37, -97
Let's plot these points on a scatterplot:
(x, y) points:
(4, 40)
(8, 20)
(12, -11)
(16, -37)
(20, -97)
After plotting the points, we can analyze the trend in the data.
By observing the scatterplot, it is clear that a linear or quadratic model would not fit the data well since the points do not follow a straight line or a parabolic curve.
Next, we can try the logarithmic, exponential, and power models to see if any of them fit the data better.
Using a calculator or computer to perform the regression analysis, we find that the regression equation with the highest R² value is:
y = 82.3 - 8.275x
This equation corresponds to option : y = 82.3 - 8.275x
The regression equation represents a linear model that best fits the given data. The R² value indicates how well the model explains the variability in the data, and in this case, the linear model provides the highest R² value compared to the other models.
It's important to note that the specific values of the coefficients in the regression equation may vary slightly depending on the calculator or software used for the analysis. However, the overall best-fit model remains the same.
For more such questions on mathematical model
https://brainly.com/question/28592940
#SPJ8
Help me pleaseee!!
Would appreciate ^^
**BRAINLIST, thanks and points***
Number 3
Plssss answer

Answers
Answer:
18.01
Step-by-step explanation:
20.10 - 2.09 = 18.01
Answer:
18.01 million
Step-by-step explanation:
Local autorety housing: 20.10
Servises to public: 2.09
Local authorety housing-servises to public= Differnece.
20.10-2.09=18.01
Solving for Unknown Angle Measures
GEE
9
If angle 1 is 110°, what would the other angle
measures have to be in order for m | n and
all p?
4
Angle 2 =
3
n
Angle 3 =
2
Angle 4 =
m
Answers
Answer:
angle 4 is a full angle because it is represented full 110
Answer:
1 - 110
2 - 110
3 - 70
4 - 70
Economic growth typically results in rising standards of living and prosperity. However, it also invites negative externalities such as environmental degradation due to over- exploiting of natural resources. As such, the world is confronted with the dilemma of growth versus environmental sustainability. Developing a model explaining the disparity of economic development concentrating on drivers such as tourism sustainability, technological innovation and the quality of leadership would be important not only to facilitate future economic growth in developing countries, but also to the environmental and sociocultural sustainability which ultimately lead to global sustainable development. The present research objective is to develop and test framework of sustainable development by considering the elements of tourism, technological innovation, and national leadership. This further would facilitate growth, environmental and socio-cultural sustainability. Understanding the integration of these dimensions would enable the building of a Sustainable Development Framework (SDF) that would provide better insight in promoting the SDGS agenda. Ultimately, growth and environmental sustainability can be achieved which will benefit the society, the economy, and nations and of course for future sustainable policy recommendation. Based on the issue above, you are required to propose relevant econometric approaches with the aims to test sustainable development by considering the elements of tourism, technological innovation, and national leadership. Question 1 [10 marks] [CLO2] Based on the scenario above, a. Propose an appropriate model specification based on the scenario above. [4 marks] used in the [4 marks] [2 marks] b. Justify the selection of the dependent and independent variables model. c. Justify the selection of the sample period.
Answers
According to the given information, the sample period should be from 2010-2020.
a) Model specification
The model specification based on the scenario above is as follows:
SDF= f(T, TI, NL)
Where: SDF= Sustainable Development Framework
T= Tourism
TI= Technological innovation
NL= National leadership
b) Justification for the selection of the dependent and independent variables model:
Dependent variable: The dependent variable in this model is Sustainable Development Framework (SDF). The model seeks to develop a framework for sustainable development that would facilitate growth, environmental and socio-cultural sustainability.
Independent variables:
The independent variables are tourism sustainability, technological innovation, and quality of leadership. These variables drive economic development. The inclusion of tourism sustainability reflects its importance in the global economy and its potential to drive growth.
The inclusion of technological innovation reflects its potential to enhance productivity and create new industries. The inclusion of national leadership reflects the role of governance in promoting sustainable development and managing negative externalities.
c) Justification for the selection of the sample period:
The sample period should be selected based on the availability of data for the variables of interest. Ideally, the period should be long enough to capture trends and patterns in the data. However, it should not be too long that the data becomes obsolete or no longer relevant.
Additionally, the period should also reflect the context and relevance of the research question. Therefore, the sample period for this study should cover the last decade to capture the trends and patterns in the data and reflect the relevance of the research question.
The sample period should be from 2010-2020.
To know more about Model specification, visit:
https://brainly.com/question/13326948?
#SPJ11
What is the slope of the line?
a. 3
b. 1/3
c. -1/3
d. -3

Answers
Answer:
B. 1/3
Step-by-step explanation:
If you look at points (-3,0) and point (0,1). Then you would see the it would take one unit up and 3 units right this would make the slope be 1/3.
please hekp and show work
Answers
The angles in the figures are supplementary and x values are 32, 30, 32 and 50.
Two angles are considered supplementary if the sum of their measures is 180 degrees.
Two angles are considered complementary if the sum of their measures is 90 degrees.
The given two angles are supplementary which makes a sum of 180 degrees.
x+20+128=180
x+148=180
Subtract 148 from both sides:
x=180-148
x=32
ii) Now x-3+153=180
x+150=180
x=30
iii) 84+3x=180
3x=180-84
3x=96
x=32
iv) 30+x+2x=180
30+3x=180
3x=150
x=50
To learn more on Angles click:
https://brainly.com/question/28451077
#SPJ1
ASAPPPP ANDWERRR FOR BRAINLIEST

Answers
Answer:
4^0
Step-by-step explanation:
4^(5 - 7 - (-2)) = 4^0 = 1
In ΔRST, r = 18 inches, s = 46 inches and ∠T=158°. Find ∠R, to the nearest degree.
Answers
Check the picture below.
let's firstly find side "t"
\(\textit{Law of Cosines}\\\\ c^2 = a^2+b^2-(2ab)\cos(C)\implies c = \sqrt{a^2+b^2-(2ab)\cos(C)} \\\\[-0.35em] ~\dotfill\\\\ t = \sqrt{18^2+46^2~-~2(18)(46)\cos(158^o)} \implies t = \sqrt{ 2440 - 1371168 \cos(158^o) } \\\\\\ t \approx \sqrt{ 2440 - (-1535.42) } \implies t \approx \sqrt{ 3975.42 } \implies t \approx 63.05 \\\\[-0.35em] ~\dotfill\)
\(\textit{Law of Sines} \\\\ \cfrac{\sin(\measuredangle A)}{a}=\cfrac{\sin(\measuredangle B)}{b}=\cfrac{\sin(\measuredangle C)}{c} \\\\[-0.35em] ~\dotfill\\\\ \cfrac{\sin( R )}{18}\approx\cfrac{\sin( 158^o )}{63.05}\implies 63.05\sin(R)\approx18\sin(158^o) \\\\\\ \sin(R)\approx\cfrac{18\sin(158^o)}{63.05} \implies R\approx\sin^{-1}\left( ~~ \cfrac{18\sin( 158^o)}{63.05} ~~\right)\implies \boxed{R\approx 6.14^o}\)
Make sure your calculator is in Degree mode.

3. The table shows the linear relationship between the balance of a student's savings account and the number of weeks she has been saving. Savings Account Week 0 1 2 4 7 12 Balance (dollars) 24 32 40 56 80 120 Based on the table, what was the rate of change of the balance of the student's savings account in dollars and cents per week?
Answers
The number of weeks are 0 1 2 4 7 12
The balances are 24 32 40 56 80 120
The rate of change of the balance of the student's savings account in dollars and cents per week is also referred to as the slope of the graph that can be potted with these values. The formula for slope is expressed as
Slope = (y2 - y1)/(x2 - x1)
y1 and y2 would be consecutive values of the balance
x1 and x2 would be consecutive values of the number of weeks
When x1 = 0, y1 = 24
When x2 = 1, y1 = 32
Slope = (32 - 24)/(1 - 0)
Slope = 8
The rate of change of the balance of the student's savings account in dollars and cents per week is 8 dollars per week. Converting to cents, it would be 800 cents per week
Arthur drops a ball from a height of 81 feet above the ground. Its height, h, is given by the equation h = –16t2 + 81, where t is the time in seconds. For which interval of time is the height of the ball less than 17 feet?
Answers
Answer:
Step-by-step explanation:
We are given the position function and need to find the value of t when h<17.
Create an inequality that represents this situation:
\(-16t^2+81<17\) The "less than" sign makes this very specifically a conjunction problem as opposed to a disjunction. That's important to the solution. But we'll get there.
The simplest way to solve this is to subtract 81 from both sides:
\(-16t^2<-64\) then divide both sides by -16:
\(t^2>4\) Notice now that the sign is facing the other way since we had to divide by a negative number. Now it's a disjunction. The solution set to this inequality is that t>2 or t<-2. First and foremost, time will never be negative, so we can disregard the -2. Even if that was t<2, the more time that goes by, the greater the time interval is, not the lesser. It's the "<" that doesn't make sense, not only the -2. The solution to this inequality is
t > 2 sec. That means that after 2 seconds, the height of the ball is less than 17 feet.
Answer:
A on edg
Step-by-step explanation:
Look at points C and D on the graph:
What is the distance (in units) between points C and D? Round your answer to the nearest hundredth.
A. 3.46 units
B. 8.49 units
C. 12.00 units
D.72.00 units

Answers
Answer:
B
Step-by-step explanation:
\( \sqrt{( - 4 - 2) {}^{2} + (6 - 0) {}^{2} } = 8.49 \\ \)
Answer:
B. 8.49
Step-by-step explanation:
Just took the same test
√6 x √27 is equal to
Answers
Answer:
square root 162
Step-by-step explanation:
Answer:
\(9 \sqrt{2 } \)
An artist draws a square chalk mural with side length a. The artist decides to enlarge the mural. The area of the new mural is represented by (5a)(3a + 2).
Simplify the expression (5a)(3a + 2).
8a + 2
15a2 + 10a
15a2 + 10
8a2 + 10a
Answers
The expression (5a)(3a + 2) simplifies to 15a^2 + 10a. This is obtained by multiplying 5a with both terms inside the parentheses using the distributive property. The final result cannot be further simplified. So, Option B is correct. Option B.
To simplify the given expression, (5a)(3a + 2), we apply the distributive property to distribute the factor 5a to both terms inside the parentheses. This involves multiplying 5a by each term separately.
First, we multiply 5a by 3a. Multiplying these two terms gives us 15a^2, where the coefficient 15 comes from multiplying 5 by 3 and the variable a is squared due to the multiplication of two a's.
Next, we multiply 5a by 2. This multiplication results in 10a, where the coefficient 10 comes from multiplying 5 by 2, and the variable a remains unchanged.
Combining the two simplified terms, we have 15a^2 + 10a. This expression cannot be further simplified because there are no like terms to combine.
The term 15a^2 represents the enlarged area of the mural, obtained by multiplying the lengths of the sides of the original square mural (side length a) by the factor 5 and squaring the variable a. The term 10a represents an additional area added during the enlargement process, obtained by multiplying the side length a by the factor 2.
In conclusion, the simplified form of (5a)(3a + 2) is 15a^2 + 10a. So OptioN B is correct.
For more question on simplifies visit:
https://brainly.com/question/723406
#SPJ8
What is 3 and 3 over 5 times 2 and 1 over 4? hurry
Answers
Answer:81/20 or 4 1/20
Step-by-step explanation:
To solve this problem, we need to use the rules of multiplication and fractions.
First, we need to convert the mixed numbers to improper fractions:
3 and 3/5 = (5 * 3 + 3) / 5 = 18/5
2 and 1/4 = (4 * 2 + 1) / 4 = 9/4
Now we can multiply the two fractions:
(18/5) * (9/4)
To simplify this expression, we can cancel out any common factors between the numerators and denominators:
(18/5) * (9/4) = (2 * 9)/(5 * 2) * (9/4) = 9/5 * 9/4
Then, we can multiply the numerators and denominators separately:
9/5 * 9/4 = (9 * 9) / (5 * 4) = 81/20
Therefore, 3 and 3/5 times 2 and 1/4 is equal to 81/20 or 4 1/20 as a mixed number.
Answer:
Step-by-step explanation:
\(\\8 \frac{1}{10}\)
the area covered by a lake is 11 square kilometers. It is decreasing exponentially at a rate of 2 percent each year represented by A(t)=11x(.98)^t. By what factor does the area decrease in 10 years? By what factor does the area decrease each month?
Answers
Answer:
The lake decreases by a factor of 3.038 in 10 years (to 3.038 km^2).
The lake decreases by a factor of 0.00167 each month.
Step-by-step explanation:
Use the given relationship A(t)=11x(.98)^t and find the value of A for t=10 years.
A(10) = 11*(0.98)^10
A(10) = 3.621 km^2
The lake has decreased by a factor of (11km^2/3.621km^2) or 3.038.
==
The lake decreases each month by (0.02/12) or 0.00167 each month.
a youth indoor soccer team has 6 starting players. the starting players must consist of 3 boys and 3 girls. there are 7 boys and 6 girls on the team. each player can play each position. in how many ways can the coach select players to start the game?
Answers
The coach can select the 6 starting players in 20 different ways, as probability are 6 players to choose from and they must consist of 3 boys and 3 girls. There are 7 boys and 6 girls, so each player is eligible to play each position. To calculate this, the formula 6! / (3! * 3!) is used.
1. Calculate 6 factorial (6!) which is 6*5*4*3*2*1 = 720
2. Calculate 3 factorial (3!) which is 3*2*1 = 6
3. Calculate 3 factorial (3!) again which is also 6
4. Divide 6! by (3! * 3!) which is 720 / (6 * 6) = 20
When selecting a starting lineup for an indoor soccer team consisting of 6 players who must be 3 boys and 3 girls, there are 20 possible combinations. To calculate this, the coach must use the formula 6! / (3! * 3!). This formula is used to calculate the number of possible combinations when selecting a certain number of items from a set of items, where all items are unique. 6! is 6 factorial, which is calculated by multiplying the numbers from 6 down to 1 (6*5*4*3*2*1). 3! is 3 factorial, which is calculated by multiplying the numbers from 3 down to 1 (3*2*1). When 6! is divided by the product of 3! multiplied by 3!, the result is 20. This shows that the coach can select the 6 starting players in 20 different ways, as there are 6 players to choose from and they must consist of 3 boys and 3 girls. There are 7 boys and 6 girls, so each player is eligible to play each position.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
Suppose we know the prices of zero-coupon bonds for different maturities with par values all being $1,000. The price of a one-year zero coupon bond is $959.63; The price of a two-year zero- coupon bond is $865.20; The price of a three-year zero-coupon bond is $777.77; The price of a four-year zero-coupon bond is $731.74. What is, according to the liquidity performance hypothesis, the expected forward rate in the third year if ∆ is 1%? What is the yield to maturity on a three-year zero-coupon bond?
Answers
According to the liquidity preference hypothesis, the expected forward rate in the third year when ∆ is 1% is 12.18%, and the yield to maturity on a three-year zero-coupon bond is 10.35%.
According to the liquidity preference hypothesis, the interest rate for a long-term investment is expected to be equal to the average short-term interest rate over the investment period. In this case, the expected forward rate for the third year is stated as 4.28%.
To calculate the expected forward rate for the third year, we first need to calculate the prices of zero-coupon bonds for each year. Let's start by calculating the price of a four-year zero-coupon bond, which is determined to be $731.74.
The rate of return on a four-year zero-coupon bond is then calculated as follows:
Rate of return = (1000 - 731.74) / 731.74 = 0.3661 = 36.61%.
Next, we use the yield of the four-year zero-coupon bond to calculate the price of a three-year zero-coupon bond, which is found to be $526.64.
The expected rate in the third year can be calculated using the formula:
Expected forward rate for year 3 = (Price of 1-year bond) / (Price of 2-year bond) - 1
By substituting the values, we find:
Expected forward rate for year 3 = ($959.63 / $865.20) - 1 = 0.1088 or 10.88%
If ∆ (delta) is 1%, we can calculate the expected forward rate in the third year as follows:
Expected forward rate for year 3 = (1 + 0.1088) × (1 + 0.01) - 1 = 0.1218 or 12.18%
Therefore, according to the liquidity preference hypothesis, the expected forward rate in the third year, when ∆ is 1%, is 12.18%.
Additionally, the yield to maturity on a three-year zero-coupon bond can be calculated using the formula:
Yield to maturity = (1000 / Price of bond)^(1/n) - 1
Substituting the values, we find:
Yield to maturity = (1000 / $526.64)^(1/3) - 1 = 0.1035 or 10.35%
Hence, the yield to maturity on a three-year zero-coupon bond is 10.35%.
In conclusion, according to the liquidity preference hypothesis, the expected forward rate in the third year when ∆ is 1% is 12.18%, and the yield to maturity on a three-year zero-coupon bond is 10.35%.
Learn more about interest rate
https://brainly.com/question/28272078
#SPJ11
1. Simplify the expression:
4+36+(10-8)’-3+7
A. 130
B. 100
C. 38
D. 37
Answers
Answer:
The answer isn't in the options anyway I'll write it. the answer is 46.
Step-by-step explanation:
According to BODMAS rule - addition should be done first so
4+36= 40 and -3 +7 = 4 so 40+4 ,= 44
then we should do subtracting so, 10-8 = 2
to conclude we should bring the equation to an end so,
44+2 = 46
HOPE THIS HELPS YOU