A spinner has three sections which are coloured red, green and blue. Chris spun the spinner 100 times in total. The frequency of spins that landed on green was 35. The ratio of the frequency of red to the frequency of green was 4:7. What is the estimated probability of the spinner landing on blue? Give your answer as a decimal.
Answers
The following is the predicted likelihood that the spinner will land on blue is 0.25
What is frequency?Frequency is a term used to describe how often a particular event or phenomenon occurs within a given period of time.
According to question:We can start by using the ratio of red to green frequency to find the frequency of red spins:
Let x be the frequency of red spins
Then the frequency of green spins is 7x/4 (since the ratio of red to green frequency is 4:7)
And the frequency of blue spins is 100 - x - 7x/4 (since there are a total of 100 spins)
We also know that the frequency of green spins is 35:
7x/4 = 35
7x = 140
x = 20
So the frequency of red spins is 20, and the frequency of blue spins is:
100 - 20 - 7(20)/4 = 25
Hence, the following is the predicted likelihood that the spinner will land on blue:
25/100 = 0.25
So the answer as a decimal is 0.25.
Learn more about frequency visit:
https://brainly.com/question/5102661
#SPJ1
Related Questions
Pam is placing a bird feeder in a tree in her back yard. She first needs to put up a 10-inch wooden platform in the fork of two tree branches that make a 52° angle, as shown below. What equation can Pam use to determine xthe distance up the tree trunk from the fork at she should drill attach the platform?
Answers
Answer:
\(x = \frac{10}{\tan(52^o)}\)
Step-by-step explanation:
Given
See attachment for illustration
Required
Equation to find x
The relationship between angle \(52^o\) and side lengths x and 10 inches is by tangent formula which is given by:
\(\tan(\theta) = \frac{Opposite}{Adjacent}\)
So, we have:
\(\tan(52^o) = \frac{10}{x}\)
Make x the subject
\(x = \frac{10}{\tan(52^o)}\)

PLEASE I NEED HELP ASAP! The function below represents the interest Jessi earns on an investment. Identify the term that represents the amount of money originally invested. f(x) = 1,000(1 + 0.05)x 1,000 1 0.05 1.05
Answers
Answer:
1000
Step-by-step explanation!
The formula for the amount accrued [ƒ(x)] on an investment earning compound interest is f(t) = P(1 + r)^t where:
P = the amount of money invested (the principal)
r = the interest rate per payment period expressed as a decimal fraction
t = the number of periods
Your formula is
f(x) = 1000(1 + 0.05)^x
In comparison, we can see that the term that represents the amount of money originally invested is 1000.
Answer:
(A) 1,000
Step-by-step explanation:
i just took the test
use double integrals to find the area inside the curve r = 3 + sin(θ).
Answers
The area inside the curve r = 3 + sin(θ) is (5π)/2 square units.
Double integration is an important tool in calculus that allow us to calculate the area of irregular shapes in the Cartesian coordinate system. In particular, they are useful when we are dealing with shapes that are defined in polar coordinates.
To find the area inside this curve, we can use a double integral in polar coordinates. The general form of a double integral over a region R in the xy-plane is given by:
∬R f(x,y) dA
where dA represents the infinitesimal area element, and f(x,y) is the function that we want to integrate over the region R.
In polar coordinates, we can express dA as r dr dθ, where r is the distance from the origin to a point in the region R, and θ is the angle that this point makes with the positive x-axis. Using this expression, we can write the double integral in polar coordinates as:
∬R f(x,y) dA = ∫θ₁θ₂ ∫r₁r₂ f(r,θ) r dr dθ
where r₁ and r₂ are the minimum and maximum values of r over the region R, and θ₁ and θ₂ are the minimum and maximum values of θ.
To find the area inside the curve r = 3 + sin(θ), we can set f(r,θ) = 1, since we are interested in calculating the area and not some other function. The limits of integration can be determined by finding the values of r and θ that define the region enclosed by the curve.
To do this, we first note that the curve r = 3 + sin(θ) represents a cardioid, which is a type of curve that is symmetric about the x-axis. Therefore, we only need to consider the region in the first quadrant, where 0 ≤ θ ≤ π/2.
To find the limits of integration for r, we note that the curve intersects the x-axis when r = 0. Therefore, the minimum value of r is 0. The maximum value of r can be found by setting θ = π/2 and solving for r:
r = 3 + sin(π/2) = 4
Therefore, the limits of integration for r are r₁ = 0 and r₂ = 4.
The limits of integration for θ are simply θ₁ = 0 and θ₂ = π/2, since we are only considering the region in the first quadrant.
Putting it all together, we have:
Area = ∬R 1 dA
= ∫\(0^{\pi /2}\) ∫0⁴ 1 r dr dθ
Evaluating this integral gives us:
Area = π(3² - 2²)/2 = (5π)/2
Therefore, the area inside the curve r = 3 + sin(θ) is (5π)/2 square units.
To know more about Integration here
https://brainly.com/question/18125359
#SPJ4

Using double integrals, the area inside the curve r = 3 + sin(θ) is 0 units².
For the area inside the curve r = 3 + sin(θ), we can use a double integral in polar coordinates. The area can be expressed as:
A = ∬R r dr dθ
where R represents the region enclosed by the curve.
In this case, the curve r = 3 + sin(θ) represents a cardioid shape. To determine the limits of integration for r and θ, we need to find the bounds where the curve intersects.
To find the bounds for θ, we set the expression inside sin(θ) equal to zero:
3 + sin(θ) = 0
sin(θ) = -3
However, sin(θ) cannot be less than -1 or greater than 1. Therefore, there are no solutions for θ in this case.
Since there are no intersections, the region R is empty, and the area inside the curve r = 3 + sin(θ) is zero.
Hence, the area inside the curve r = 3 + sin(θ) is 0 units².
To know more about double integrals refer here:
https://brainly.com/question/27360126#
#SPJ11
Select the correct answer.
Which statement is false?
A.
The inequality sign always opens up to the larger number.
B.
The greater number in an inequality is always above the other number on the vertical number line.
C.
The smaller number in an inequality is always located to the left of the other number on the horizontal number line.
D.
The inequality sign always opens up to the smaller number
Answers
Answer:
I think it might be C or B
Step-by-step explanation:
Hope this helped have a nice day :)
A baby can walk ⅛ of a meter in 1/24 of an hour. How many meters can they walk in 4 hours?
Answers
Answer:
I didn't understand the question well is it 1.8meter in 1h24m if so then here is my answer
Step-by-step explanation:
so basically to make things easy for me I convert hours to minutes 4h is 4×60=240minutes 1h24min= 84min right
so if I baby walks 1.8m in a 84min then in a 240min they gonna walk X meter
84min-->1.8m
240min--> X
so 240×1.8÷84=5.14
So a baby will walk 5.14m in 4H
Write an equation for the hyperbola that satisfies the given set of conditions.
Vertices (20,0) and (-20,0) conjugate axis of length 18 units.
Answers
The vertices of the hyperbola are the x-intercepts of the hyperbola
The equation of the hyperbola is \(\frac{y^2}{400} -\frac{x^2}{81} = 1\)
How to determine the equation of the hyperbola?The equation of a hyperbola is represented as:
\(\frac{(y - k)^2}{a^2} -\frac{(x - h)^2}{b^2} = 1\)
The vertices are (20,0) and (-20,0).
So, the center of the hyperbola is:
(h,k) = (0,0).
Also, we have:
a = 20
This gives
\(\frac{(y - 0)^2}{a^2} -\frac{(x - 0)^2}{b^2} = 1\)
Evaluate
\(\frac{y^2}{a^2} -\frac{x^2}{b^2} = 1\)
Substitute 20 for a
\(\frac{y^2}{20^2} -\frac{x^2}{b^2} = 1\)
\(\frac{y^2}{400} -\frac{x^2}{b^2} = 1\)
The length of the conjugate axis is:
l = 18 units
So, we have:
\(b = \frac{18}2 = 9\)
The equation becomes:
\(\frac{y^2}{400} -\frac{x^2}{9^2} = 1\)
\(\frac{y^2}{400} -\frac{x^2}{81} = 1\)
Hence, the equation of the hyperbola is \(\frac{y^2}{400} -\frac{x^2}{81} = 1\)
Read more about hyperbola at:
https://brainly.com/question/26250569
what is the anwser to 40.5 - 5.35
Answers
It is 35.15. Hope it helps
⚠️HELP PLZZZ ⚠️‼️help plz I’ve been on this question for an while now and I don’t understand
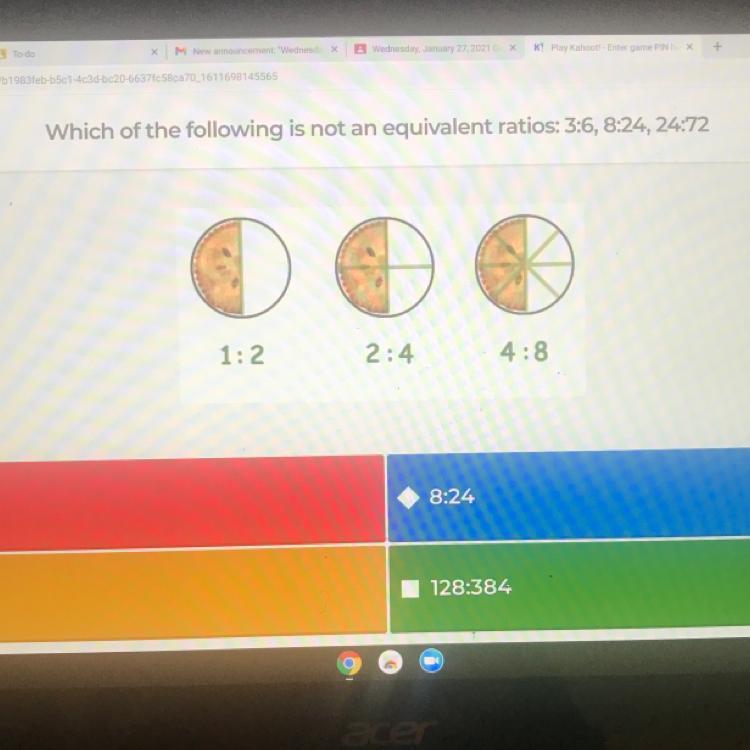
Answers
Answer:
3:6
Step-by-step explanation:
8:24 and 24:72 reduce down to 1:3. 3:6 is 1:2.
a) 3x2+y4x2x6y
Х
Simplified
Answers
Answer:
x9y5+3x2
Step-by-step explanation:
3x2+y4x2x6yx
=3x2+x9y5
Distribute an amount of Rs. 200 between Raheem and Usman such that Raheem
gets RS 50 more than twice as much as Usman gets .
Answers
Answer:
50 and 150
Step-by-step explanation:
Raheem- (2x+50)
Usman- x
(2x+50)+x=200
3x+50=200
3x=150
x=50
plug in the numbers
finding volume of sphere when r=6
Answers
Answer:
V = 904.78
Step-by-step explanation:
Volume of a Sphere = 4π\(\frac{r^3}{3}\)
=> V = 4π\(\frac{6^3}{3}\)
=> V = 4π\(\frac{216}{3}\)
=> V = 4π(72)
=> V = 904.78
Hope this helps!
Please help!! I have 10 minutes left!!

Answers
Suppose you have a bag containing 2 black marbles and 3 red marbles. You reach into the bag, select a marble, see what color it is and replace it in the bag. Then you repeat this process a second time. What is the probability of picking a red marble both times?
Answers
Answer:
\(\dfrac{9}{25}\)
Step-by-step explanation:
Given that the bag contains black and red marbles.
Number of black marbles in the bag = 2
Number of red marbles in the bag = 3
Total number of marbles in the bag = Number of black marbles + Number of red marbles = 2 + 3 = 5
Let us have a look at the formula for probability of an event E, which can be observed as:
\(P(E) = \dfrac{\text{Number of favorable cases}}{\text {Total number of cases}}\)
\(P(\text{First red marble}) = \dfrac{\text{Number of red marbles}}{\text{Total number of marbles}} = \dfrac{3}{5 }\)
Now, the marble chosen at first is replaced.
Therefore, the count remains the same.
\(P(\text{Second red marble}) = \dfrac{\text{Number of red marbles}}{\text{Total number of marbles}} = \dfrac{3}{5}\)
Now, the required probability can be found as:
\(P(\text{First red marble})\times P(\text{Second red marble}) = \dfrac{3}{5}\times \dfrac{3}{5} = \bold{\dfrac{9}{25} }\)
Zeno jumped 8 meters. Then he jumped half as far again (4 meters). Then he jumped half as far again (2 meters). So after 3 jumps, he was 8 + 4 + 2 = 14 meters from his starting place.
a. Zeno kept jumping half as far again. How far would he be after 4 jumps?
Answers
14/2 = 7
7/2 = 3.5
3.5/2 = 1.75
1.75/2 = 0.875
9514 1404 393
Answer:
15 meters
Step-by-step explanation:
Zeno's last jump was 2 meters, so another jump half as far adds 1 meter to the 14 m total.
After 4 jumps, Zeno would have jumped 15 meters from his starting place.
__
Comment on the question
The given distances give a total "after 3 jumps." The question asks for a total "after 4 jumps." It is not clear whether that is 4 jumps total, or 4 more jumps. In the above, we have assumed it is 4 jumps total.
Use the drawing tool(s) to form the correct answer on the provided number line.
Consider the given functions.
Function 1
f(x) = -5x + 11 + 10
Function 2
g(x)
-2
Represent the interval where both functions are decreasing on the number line provided.
30
20
10-
-10-
-20-
-30-
2
6
x

Answers
\((-1,\infty)\cap (-2,2) ---- > (-1,2)\)
What is the function's decreasing in the interval?Generally, the equation for the function is mathematically given as
f(x) = -5x + 11 + 10
Therefore
When x >= -1, the function decreases because f(x) = -5(x+1)+10.
This means that the function is dropping throughout this range\((-1,\infty).\)
b)
A look at the graph reveals a decreasing trend in the function over the timeframe (-2,2).
In conclusion, The number line will represent
Using the point where the intervals with decreasing functions overlap
\((-1,\infty)\cap (-2,2) ---- > (-1,2)\)
Read more about inequalities
https://brainly.com/question/20383699
#SPJ1
Answer:
see photos
Step-by-step explanation:
Plato/Edmentum


HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP
HELP I NEED HELP ASAP

Answers
(Not an expert, just a guess)
Use the summation formulas to rewrite the expression without the summation notation. 6k(k -1) k 1 S(n) = 3 Use the result to find the sums for n n 10 2-2.53 n = 100 n 1,000 n = 10,000 51 10, 100, 1000, and 10,000.
Answers
For n = 10: -3.8981
For n = 100: -398.4496
For n = 1000: -38886.3254
For n = 10000: -388823.2811.
The given expression in summation notation is:
S(n) = Sum[6k(k-1) / (k+1), {k,1,n}]
We can use the summation formula for k(k-1) and write it as \(k^2 - k\), and the summation formula for 1/(k+1) and write it as ln(k+1). Substituting these in the expression above, we get:
\(S(n) = Sum[6k^2/(k+1) - 6k/(k+1), {k,1,n}]\\ = Sum[6k^2/(k+1), {k,1,n}] - Sum[6k/(k+1), {k,1,n}]\\ = Sum[6k^2/(k+1), {k,1,n}] - Sum[6/(1+1/k), {k,1,n}]\\ = Sum[6k^2/(k+1), {k,1,n}] - 6Sum[1+1/(k+1), {k,1,n}]\\ = Sum[6k^2/(k+1), {k,1,n}] - 6Sum[1, {k,1,n}] - 6Sum[1/(k+1), {k,1,n}]\\ = Sum[6k^2/(k+1), {k,1,n}] - 6n - 6Sum[1/(k+1), {k,1,n}]\\ = Sum[6k^2/(k+1), {k,1,n}] - 6n - 6(ln(n+1) - ln(2))\)
Now, we can use this formula to find the values of S(n) for different values of n.
For n = 10:
\(S(10) = (6\times 1^{2/2} + 6\times 2^{2/3} + ... + 6\times 10^{2/11}) - 6\times 10 - 6(ln(11) - ln(2))= -3.8981\)
For n = 100:
\(S(100) = (6\times 1^{2/2 }+ 6\times 2^{2/3} + ... + 6\times 100^{2/101}) - 6\times 100 - 6(ln(101) - ln(2))= -389.4496\)
For n = 1000:
\(S(1000) = (6\times 1^{2/2} + 6\times 2^{2/3 }+ ... + 6\times 1000^{2/1001}) - 6\times 1000 - 6(ln(1001) - ln(2))= -38886.3254\)
For n = 10000:
\(S(10000) = (6\times 1^{2/2} + 6\times 2^{2/3} + ... + 6\times 10000^2/10001) - 6\times 10000 - 6(ln(10001) - ln(2))= -388823.2811\)
for such more question on summation notation
https://brainly.com/question/16599038
#SPJ11
evaluate -a + (-b) where a= 6.05 and b= 3.611
Answers
Answer:
-6.05+(-3.611)=-9.661
Step-by-step explanation:
A machinist creates a solid steel part for a wind turbine engine. The part has a volume of 1015 cubic centimeters. Steel can be purchased for 29 fils per kilogram and has a density of 7. 95 g/cm3. If the machinist makes 500 of these parts, what is the cost of the steel, to the nearest dirham?.
Answers
If the machinist makes 500 of these parts, the cost of the steel is 1170 dirham ( rounds to the nearest dirham).
We have, A machinist creates a solid steel part for a wind turbine engine. Let us consider volume, mass and density of steel part be "V", "M", "D" respectively.
Density of a material is defined as mass of material per unit volume of material,
D = M/V .
Volume of steel part, V = 1015 cm³
The cost of steel part = 29 fils per kg
Density of steel part, D = 7. 95 g/cm³
Number of steel part used by machinist
= 500
So, Denssity = Mass of steel part/ Volume of steel part
=> 7. 95 g/cm³ = M/1015 cm³
=> M = 7.95× 1015 g
=> M = 8,069.25 g
Now, Convert the mass of steel part from grams to kilograms using conversion units.
Mass of steel part, M = 8,069.25/1000 g
=> M = 8.07 kg
So, cost of one steel part = 29 fils/kg × 8.07 kg = 234.008 ~ 234 fils
If the machinist makes 500 of these parts, the cost of the steel = 500× 234
= 117,000 fils.
But we wants the cost of steel in dirham so we have to convert the fils units into dirham units,
One dirham is divided into 100 fils.
So, 117,000 fils = 117,000/100 dirham
= 1170 dirham.
Thus, required cost of steel is 1170 dirham.
To learn more about Density , refer:
https://brainly.com/question/26364788
#SPJ4
3/5 of a number is 162. Work out the number. How do I do this AQA question?
Answers
Answer:
The number is 270
Step-by-step explanation:
Let the number be 'x'
3/5 of x = 162
\(\frac{3}{5}*x = 162\\\\x=162*\frac{5}{3}\\\\x=54 * 5\\\\x = 270\)
Answer:
\( \boxed{ \bold{ \huge{ \boxed{ \sf{270}}}}}\)
Step-by-step explanation:
Let the number be 'x'
\( \sf{ \frac{3}{5 } \: \: of \: x \: = 162}\)
⇒\( \sf{ \frac{3x}{5} = 162}\)
Apply cross product property
⇒\( \sf{3x = 162 \times 5}\)
Multiply the numbers
⇒\( \sf{3x = 810}\)
Divide both sides of the equation by 3
⇒\( \sf{ \frac{3x}{3} = \frac{810}{3} }\)
Calculate
⇒\( \sf{x = 270}\)
Hope I helped!
Best regards!!
Tony is using the numbers 12 7 4 1 to make a new number?
Answers
Step-by-step explanation:
Given:
To find:
Solution:
(multiplication of digits give a larger number compared to addition, subtraction and division)
= (12 × 7) × (4 + 1)
∴ The biggest number Tony can make is 420.
A paper company needs to ship paper to a large printing business. The paper will be
shipped in small boxes and large boxes. The volume of each small box is 6 cubic feet
and the volume of each large box is 22 cubic feet. A total of 22 boxes of paper were
shipped with a combined volume of 324 cubic feet. Write a system of equations that
could be used to determine the number of small boxes shipped and the number of
large boxes shipped. Define the variables that you use to write the system.
Answers
Answer:
10 small boxes and 12 large boxes
Step-by-step explanation:
Let x = number of large boxes
Let y = number of small boxes
We are told that;
volume of each small box = 6 cubic feet
volume of each large box = 22 cubic feet.
Total volume = 324 ft³
Thus;
6x + 22y = 324 - - - (eq 1)
We are told that 22 boxes of paper were shipped.
Thus; x + y = 22 - - - (eq 2)
Making x the subject in eq 2 gives;
x = 22 - y
Put 22 - y for x in eq 1;
6(22 - y) + 22y = 324
132 - 6y + 22y = 324
16y = 324 - 132
16y = 192
y = 192/16
y = 12
So, x = 22 - 12 = 10
What is the value of the expression below when c=5 and d=4?

Answers
Answer:
138.....................
Answer:
888
Step-by-step explanation:
C equals 5 so u do 6 times 5. Then you have to do that by the exponent of 2 which equals 900. Because d equals 4 u do 5 times 4 which equals 20. So 900 minus 20 equals 880 plus 8 equals 888
18 pizzas were ordered for a holiday party at Reedy Creek Elementary

Answers
ANSWER
C. 12
EXPLANATION
1/3 of the pizzas is:
\(18\times\frac{1}{3}=\frac{18}{3}=6\)Therefore, 6 pizzas were cheese and the rest were pepperoni:
\(18-6=12\)There were 12 pepperoni pizzas.
I NEED HELP WITH THIS MATH PROBLEM !!

Answers
An equation that relates T to N can be written as T = 750 + 560N.
What is an equation?An equation can be defined as a mathematical expression which shows that two (2) or more thing are equal.
What is a function?A function can be defined as a mathematical expression which can be used to define and represent the relationship that exist between two or more variables in a population (data set).
How to write an equation relating T to N.Since the total amount saved by using both plans (functions A and B) is represented by T, an equation that relates T to N can be written as follows:
T = A + B
Substituting the given parameters into the formula, we have;
T = (750 + 165N) + 395N
T = 750 + 165N + 395N
T = 750 + 560N.
Read more on function here: https://brainly.com/question/19537858
#SPJ1
Complete Question:
Ann and her husband are each starting a saving plan. Ann will initially set aside $750 and then add $165 every month to the savings. The amount A (in dollars) saved this way is given by the function A=750+165N , where N is the number of months he has been saving. Her husband will not set an initial amount aside but will add $395 to the savings every month. The amount B (in dollars) saved using this plan is given by the function B=395N. Let T be total amount (in dollars) saved using both plans combined. Write an equation relating T to N.
Simplify your answer as much as possible.
Sensitivity analysis: It is sometimes useful to express the parameters a and b in a beta distribution in terms of θ0=a/(a+b) and n0=a+b, so that a=θ0n0 and b=(1−θ0)n0. Reconsidering the sample survey data in Problem 4, for each combination of θ0∈{0.1,0.2,…,0.9} and n0∈{1,2,8,16,32} find the corresponding a,b values and compute Pr(θ>0.5∣∑Yi=57) using a beta (a,b) prior distribution for θ. Display the results with a contour plot, and discuss how the plot could be used to explain to someone whether or not they should believe that θ>0.5, based on the data that ∑i=1100Yi=57.
Answers
The contour plot shows that the probability that θ > 0.5 increases as θ0 increases and n0 increases. This means that if we believe that θ is close to 0.5, and we have a lot of data, then we are more likely to believe that θ is actually greater than 0.5.
The contour plot is a graphical representation of the probability that θ > 0.5, as a function of θ0 and n0. The darker the shading, the higher the probability. The plot shows that the probability increases as θ0 increases and n0 increases. This is because a higher value of θ0 means that we believe that θ is more likely to be close to 0.5, and a higher value of n0 means that we have more data, which makes it more likely that θ is actually greater than 0.5.
The plot can be used to explain to someone whether or not they should believe that θ > 0.5, based on the data that ∑i=1100Yi=57. If we believe that θ is close to 0.5, and we have a lot of data, then we should be more likely to believe that θ is actually greater than 0.5. However, if we believe that θ is far from 0.5, or if we don't have much data, then we should be less likely to believe that θ is actually greater than 0.5.
To learn more about contour plot click here : brainly.com/question/32524101
#SPJ11
Which of the following values does not satisfy the inequality X - 7 > 12?
A 11
B 33
C 22
D 44
Answers
Answer:
We conclude that when we put x = 11, it does not satisfy the inequality.
Hence, option (A) is correct.
Step-by-step explanation:
Given the inequality
x - 7 > 12
Any value which makes the inequality FALSE would be the value that not satisfy the inequality.
Putting x = 11 in the inequality
x - 7 > 12
11 - 7 > 12
4 > 12
FALSE!
Reason: 4 can not be greater than 12
Putting x = 33 in the inequality
x - 7 > 12
33 - 7 > 12
26 > 12
TRUE!
Reason: 26 is indeed greater than 12
Putting x = 22 in the inequality
x - 7 > 12
22 - 7 > 12
15 > 12
TRUE!
Reason: 15 is indeed greater than 12
Putting x = 44 in the inequality
x - 7 > 12
44 - 7 > 12
37 > 12
TRUE!
Reason: 37 is indeed greater than 12
Therefore, we conclude that when we put x = 11, it does not satisfy the inequality.
Hence, option (A) is correct.
Answer:
11
Step-by-step explanation:
Define the domain of the following:
{-2, -1, 0, 2, 5}
{-2, -1, 0, 1, 2, 3, 4, 5}
All Real Numbers
{3, -1, 3, 1, 2}

Answers
The domain of the relation in the graph is:
{-2, -1, 0, 2, 5}
How to define the domain for the graph?A relation maps elements from one set (the domain) into elements from another set (the range).
Such that the domain is represented in the horizontal axis.
In the graph, we can see the points:
{(-2, -3), (-1, -1), (0, 3), (2, 1), (5, 2)}
The domain is the set of the first values of these points, then the domain is:
{-2, -1, 0, 2, 5}
The correct option is the first one.
Learn more about domains at:
https://brainly.com/question/1770447
#SPJ1
Identify the factors of 6ab − 8a 21b − 28. (2a 4)(3b − 7) (2a − 4)(3b 7) (2a 7)(3b − 4) (2a − 7)(3b 4)
Answers
Answer: ) (2a+7)(3b- 4)
Step-by-step explanation:
Can someone solve this

Answers
Answer:
-1/2
Step-by-step explanation: