A sample of 3 different calculators is randomly selected from a group containing 10 that are defective and 5 that have no defects. Assume that the sample is taken with replacement. What is the probability that at least one of the calculators is defective? Express your answer as a percentage rounded to the nearest hundredth without the % sign.
Answers
The probability that at least one calculator is defective is approximately 96.30%.
To find the probability that at least one calculator is defective, we need to calculate the probability that all three selected calculators are not defective and subtract it from 1.
The probability of selecting a calculator without defects is
\(\frac{5}{(10+5)} = \frac{5}{15 }\)
\(= \frac{1}{3}\)
Since the selection is made with replacement, the probability of selecting three calculators without defects in a row is
\((\frac{1}{3})^3=\frac{1}{27}.\)
Since, the probability of at least one calculator being defective is
\(1 -\frac{1}{27} =\frac{26}{27}\)
To express this as a percentage rounded to the nearest hundredth, we multiply the probability by
\(100: (\frac{26}{27})\times 100 = 96.30\)
Therefore, the probability that at least one calculator is defective is approximately 96.30%.
For such more questions on probability
https://brainly.com/question/25839839
#SPJ11
Related Questions
Let Z be a standard normal random variable: i.e., Z ~ N(0,1). (1) Find the pdf of U = Z2 from its distribution. (2) Given that f(1/2) = VT Show that U follows a gamma distribution with parameter a = 1 = 1/2. (3) Show that I (1/2) = V1. Note that I (1) = Soe ex-1/2dx. Hint: Make the change of variables y = V2x and then relate the resulting expression to the normal distribution.
Answers
1)The pdf of U is f(u) = (1/(2√u)) exp(-u/2) for u > 0 and f(u) = 0 otherwise.
2)U follows a gamma-distribution with parameter a = 3/2 or a = 1/2.
3)x = (y²/2) and dx = y dy using exponential distribution
We can rewrite the integral as:
I(1/2) = ∫₀^∞ y exp(-y²) dy
= 1/2 ∫₀^∞ exp(-u/2) du
This is the same as the integral for f(u) when u = 1/2.
Therefore, we have:
I(1/2) = V1
(1) For U = Z², we can use the method of transformations.
Let g(z) be the transformation function such that
U = g(Z)
= Z².
Then, the inverse function of g is given by h(u) = ±√u.
Thus, we can apply the transformation theorem as follows:
f(u) = |h'(u)| g(h(u)) f(u)
= |1/(2√u)| exp(-u/2) for u > 0 f(u) = 0 otherwise
Therefore, the pdf of U is given by:
f(u) = (1/(2√u)) exp(-u/2) for u > 0 and f(u) = 0 otherwise.
(2) We are given that f(1/2) = VT, where V is a constant.
We can substitute u = 1/2 in the pdf of U and equate it to VT.
Then, we get:VT = (1/(2√(1/2))) exp(-1/4)VT
= √2 exp(-1/4)
This gives us the value of V.
Now, we can use the pdf of the gamma distribution to find the parameter a such that the gamma distribution matches the pdf of U.
The pdf of the gamma distribution is given by:
f(u) = (u^(a-1) exp(-u)/Γ(a)) for u > 0 where Γ(a) is the gamma function.
We can use the following relation between the gamma and the factorial function to simplify the expression for the gamma function:
Γ(a) = (a-1)!
Thus, we can rewrite the pdf of the gamma distribution as:
f(u) = (u^(a-1) exp(-u)/(a-1)!) for u > 0
We can now equate the pdf of U to the pdf of the gamma distribution and solve for a.
Then, we get:
(1/(2√u)) exp(-u/2) = (u^(a-1) exp(-u)/(a-1)!) for u > 0 a = 3/2
Therefore, U follows a gamma distribution with parameter
a = 3/2 or equivalently,
a = 1/2.
(3) We need to show that I(1/2) = V1.
Here, I(1) = ∫₀^∞ exp(-x) dx is the integral of the exponential distribution with rate parameter 1 and V is a constant.
We can use the change of variables y = √(2x) to simplify the expression for I(1/2) as follows:
I(1/2) = ∫₀^∞ exp(-√(2x)) dx
Now, we can substitute y²/2 = x to obtain:
x = (y²/2) and
dx = y dy
To know more about gamma-distribution, visit:
https://brainly.com/question/31733851
#SPJ11
can you guys please help

Answers
Answer:
I cant read all of that. Im sure others ant either.
Step-by-step explanation:
Answer:
i cant read it for some reason, can you type it?
Step-by-step explanation:
3) Simplify the expression and identify any restrictions on x.

Answers
Answer:
\(-\frac{3x+14}{x(x+5)(x-2)}\)
Step-by-step explanation:
x² + 5x = x(x + 5)
x² + 3x - 10 = ( x + 5 )( x - 2 )
x² + 5x ≠ 0 , if x ≠ 0 or x ≠ - 5
x² + 3x - 10 ≠ 0 , if x ≠ - 5 or x ≠ 2
Restrictions are: x ≠ - 5, x ≠ 0, x ≠ 2
GCD is x(x + 5)(x - 2)
Given Expression = \(\frac{7(x-2)+ 2x^2 - 2x(x+5)}{x(x+5)(x-2)}\) =
\(\frac{7x-14+2x^2 -2x^2 -10x}{x(x+5)(x-2)}\) =
\(-\frac{3x+14}{x(x+5)(x-2)}\)
Help please I’ll add more points for the answer and working out

Answers
\(▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ { \huge \mathfrak{Answer}}▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ ▪ \)
a) A = 4Bb) A = 20c) B = 9solution is in attachment !
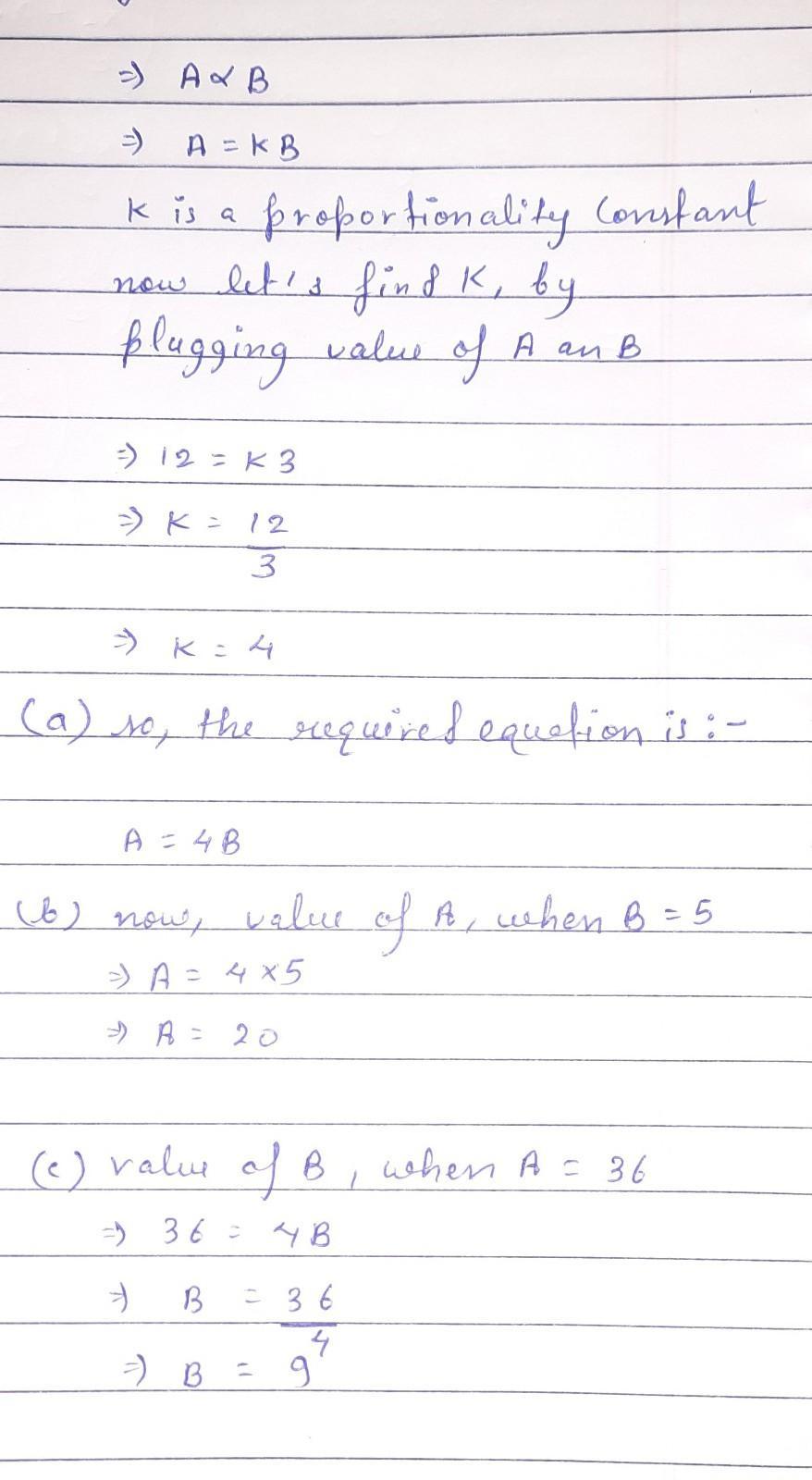
Consider the mathematical formulation below:
Minimize 4X + 12 Y subject to X+Y >= 20 (Constraint A) 4X+2Y >=60 (Constraint B) Y >= 5 (Constraint C) X>=0 and Y>=0 (Constraint D) At optimality, which of the constraints are binding (satisfied with equality)?
Answers
The binding constraints at optimality in the given mathematical formulation are Constraint B and Constraint C.
Which constraints are satisfied with equality at optimality in the provided mathematical formulation?At optimality, the mathematical formulation satisfies Constraint B and Constraint C with equality. In the given mathematical problem, the objective is to minimize the expression 4X + 12Y, subject to certain constraints. The constraints are represented by equations that limit the values of X and Y. The first constraint, Constraint A (X + Y ≥ 20), states that the sum of X and Y must be greater than or equal to 20. Constraint B (4X + 2Y ≥ 60) requires that the expression 4X + 2Y be greater than or equal to 60. Constraint C (Y ≥ 5) specifies that Y should be greater than or equal to 5. Finally, Constraint D (X ≥ 0 and Y ≥ 0) sets the lower bounds for X and Y as non-negative values.
To find the optimal solution, the mathematical formulation seeks values for X and Y that minimize the objective function (4X + 12Y) while satisfying all the constraints. In this case, the binding constraints are Constraint B and Constraint C. "Binding" means that these constraints are satisfied with equality at the optimal solution, meaning their corresponding inequalities hold as equalities. In other words, the expressions 4X + 2Y = 60 and Y = 5 are both satisfied exactly at the optimal point.
Learn more about binding constraints
brainly.com/question/32070704
#SPJ11
3/7 and 1/3 as a equvilant fraction
Answers
Answer:
3/7 + 1/3 = 1621 ≅ 0.7619048
Spelled result in words is sixteen twenty-firsts.
Step-by-step explanation:
Answer:
7/21
Step-by-step explanation:
A full glass of water can hold 1/6 of a bottle
How many glasses of water can be filled with 3 1/2 of water
Answers
Answer:
21
Step-by-step explanation:
Well you basically divide 3 and 1/2 by 1/6 which you would you have to simplify the 3 and 1/2 which is 7/2 and switch the denominator and numerator of the 1/6 which would be 6/1 and after you multiply(7/2 x 6/1=42/2) it would be 42/2 which you would have to simplify by dividing 42 and 2 which is 21. There you go I hope this helps.
Answer:
21.
Step-by-step explanation:
That would be 3 1/2 divided by 1/6.
= 7/2 / 1/6
= 7/2 * 6
= 42/2
= 21 glasses.
A square with side length 4.6 is enlarged by a factor of 4 . What is it’s new area ?
Answers
Answer:
A =338.56 units ^2
Step-by-step explanation:
The area is now
A = (SF)^2 * s^2
where s is the side length and SF is the scale factor
A = (4)^2 (4.6)^2
A =338.56
(Theoretical Probability MC)
Joseph has a bag filled with 3 red, 3 green, 9 yellow, and 10 purple marbles. Determine P(not green) when choosing one marble from the bag.
92%
88%
24%
12%
Answers
The probability of not selecting a green marble is equal to the total number of non-green marbles in the bag divided by the total number of marbles in the bag.
What is the meaning of probability and it will be calculated?To calculate the probability: there are three green marbles out of a total of twenty-five marbles, so the probability of selecting a green marble is 3/25.
The likelihood of not selecting a green marble is then 1 - 3/25 = 22/25.
This is equal to 22/25 * 100 = 88% as a percentage.
As a result, P(not green) = 88%
Probability denotes the possibility of something happening. It is a mathematical branch that deals with the onset of a random event. The value ranges from zero to one. Probability has been tried to introduce in mathematics to predict the probability of events occurring. Probability is defined as the degree to which something is likely to occur. This is the fundamental probability theory, which is also used in probability distribution, in which you will learn about the possible outcomes of a random experiment.
To know more about random event visit :-
https://brainly.com/question/15186748
#SPJ1
If the Volume of a cylinder is 314in3 and diameter is 10 in, what is the height?
Answers
Answer:
314/25π inches
I hope this helps!
please help :((I need help

Answers
Answer:
See attached graph for the two functions
y = cos(x)
y = 0.5
Solution set for cos(x) i.e. the values of x for which cos(x) = 0.5 in the interval 0 < x < 2π are
{π/3, 5π/3)
or
{1.05, 5.24} in decimal
Step-by-step explanation:
I moved the original horizontal up to y = 0.5
The solutions to the two equations are where the two functions intersect
There are two intersection in the interval 0 ≤ x ≤ 2π and are at the points labeled A and B
The two points can be obtained by setting
cos(x) = 0.5 and solving for x
cos(x) = 0.5
=> x = cos⁻¹ (0.5)
= 60° and 300° in the range 0 ≤ x ≤ 2π where 2π = 360°
In terms of π,
Since π radians = 180°, 1° = π/180 radians
60° = π/180 x 60 = π/3 radians
300° = π/180 x 300 = 5π/3 radians
Therefore the solutions to cos(x) = 0.5 are
x = π/3 and x = 5π/3
The solution set is written as {π/3, 5π/3}
In decimal
π/3 = 1.04719 ≈ 1.05
5π/3 = 5.23598 ≈ 5.24
Solution set in decimal: {1.05, 5.24}

As a certain engine's rotation speed increases, its temperature increases at a constant rate. The table compares the engine's rotation speed (in cycles per second) and its temperature (in degrees Celsius).

Answers
Hey there! :)
Answer:
15° Celsius.
Step-by-step explanation:
Begin by deriving an equation to represent the values in the table. Use the slope formula:
\(m = \frac{\text{rise}}{\text{run}} = \frac{y_2 - y_1}{x_2 - x_1}\)
Plug in values from the table into the formula:
\(m = \frac{27.0 - 22.2}{15-9}\)
Simplify:
\(m = \frac{4.8}{6}\)
Reduces to:
m = 0.8. This is the slope of the equation.
Use a point from the table and plug it into the equation y = mx + b, along with the slope to calculate the y-intercept:
27 = 0.8(15) + b
27 = 12 + b
27 - 12 = b
b = 15. This represents the value when x = 0, therefore:
The engine's temperature at rest is 15° Celsius.
Answer:
15
Step-by-step explanation:
(Equivalent Algebraic Expressions LC)
Simplify this please!!

Answers
Answer:
\(\frac{x^3}{y^7}\)
Step-by-step explanation:
The key to answering this question is the exponential law that says \(a^{-n} = \frac1{a^n}$\) :
\(\frac{y^{-7}}{x^{-3}} \\ \\\to \frac{\frac1{y^7}}{\frac1{x^3}} \\ \\\to \frac1{y^7} \times \frac{x^3}1 \\ \\\to \frac{x^3}{y^7}\)
Help me please answer thanks

Answers
Answer:
I think it would be each girl scored 2 points, and each boy only scored one. :)
I don't understand this question can someone help me with this please, please explain!! and thank you for the help!! If u dont know try your best :D

Answers
Answer:
3*4 is 12, 12*4 is 48, 48*4 is 192, so the answer is 192
If m=6, then 3×6= 18.
43-18=25
Your answer is 25.
Step-by-step explanation:
Can I have brainly please!
EVALUATE EXPRESSION
Step-by-step explanation:
43-3m=?? if m=6
substitute
43-3 * 6= 25
456 - 9099 divided by 56

Answers
Answer:
293.5
Step-by-step explanation:
Harry Potter RP!!
https://brainly.com/question/20615441
need help on number 14, don’t understand part B

Answers
The number of customers when there are 576 towers will be 12.
How to calculate the word problem?A word problem in mathematics simply refers to a question that is written as a sentence or in some cases more than one sentence which requires an individual to use his or her mathematics knowledge to solve the real life scenario given.
Based on the information, it should be noted that the number of phone is proportional to the number of customers
The constant of proportionality will be:
= 252 / 5.25
= 48
Therefore, the customers when there are 576 towers will be:
= 576 / 48
= 12
Learn more about word problem on:
brainly.com/question/21405634
#SPJ1
Emma is building a bakery where she bakes brownies and large cookies. The brownies cost $4 each and the large cookies cost $6 each. She is tying to make at least $200 but wants to make no more than 75 items.
4x+6y>=200
x+y<75
Answers
The number of brownies and large cookies will be same that is 20 each.
What are inequalities ?
When two values are compared , an inequality represents whether one is greater than, less than, or not equal to the other.
It is given that the brownies cost $4 each and large cookies cost $6 each.
Let's assume the number of brownies be x and large cookies be y.
And as per the question , She is trying to make at least $200 but wants to make no more than 75 items.
So , to represent this we need an inequality which will be as follows:
Cost of x brownies = 4x
Cost of y cookies = 6y
So , inequality will be :
4x + 6y ≤ $200 --- --- --- --- --- --- --- -- - Equation 1
and
Number of brownies and cookies should not be more than 75 items. i.e.,
x + y < 75 --- --- --- --- --- --- --- -- -- -- -- -- -- Equation 2
Let's check for which value of x and y this is suitable. So , simplify equation 1 : (dividing by 2 )
2x + 3y ≤ $100
If we put x = 20 and y = 20 , then
2 × 20 + 3 × 20 = $100
$100 = $100
So , the equation is satisfied which meant the number of brownies and cookies will be equal which is 20.
Let's check it with equation 2 also :
So ,
20 + 20 < 75
40 < 75
This is also satisfied.
Therefore , the number of brownies and large cookies will be same that is 20 each.
Learn more about inequalities here :
brainly.com/question/25275758
#SPJ1
a triangle has at least 2 acute angles
(always true, never true, or sometimes true)
Answers
For example, a right triangle will have a right angle (90°) and two acute angles.
An obtuse triangle has an obtuse angle (with a measure that is greater than 90°) and two acute angles.
The three interior angles of an equilateral triangle have a measure of 60 degrees (acute angles).
An isosceles triangle can have 2 angles with a measure of 30 degrees (acute angles), and an obtuse angle (120°).
Given these examples, we can infer that the correct answer is "Always true."
3c(p-6)+4(p-6)= write the correct expression in factored form.
Answers
\(\tt\displaystyle\ 3c\underline{(p-6)}+4\underline{(p-6)}=(p-6)(3c+4)\)
One week a computer store sold a total of 36 computers and external hard drives. The revenue from these sales was 29,820. If computers sold for 1180 and hard drives for 125 per unit, how many of each were sold?
Answers
Given:
One week a computer store sold a total of 36 computers and external hard drives.
Let the number of computers = x
And the number of the external hard drives = y
so, we can write the following equation:
\(x+y=36\rightarrow(1)\)The revenue from these sales was 29,820. If computers sold for 1180 and hard drives for 125 per unit
So, we can write the following equation:
\(1180x+125y=29820\rightarrow(2)\)We will solve the equations (1) and (2) to find (x) and (y):
from equation (1):
\(y=36-x\operatorname{\rightarrow}(3)\)Substitute (y) from equation (3) into equation (2) and then solve for (x):
\(\begin{gathered} 1180x+125(36-x)=29820 \\ 1180x+125*36-125x=29820 \\ 1180x-125x=29820-125*36 \\ 1055x=25320 \\ \\ x=\frac{25320}{1055}=24 \end{gathered}\)Substitute (x) into equation (3) to find (y):
\(y=36-24=12\)So, the answer will be:
The number of computers sold = 24
The number of hard drives sold = 12
Find an equation of the tangent line to the curve xey yex = 4 at the point (0, 4).
Answers
An equation of the tangent line to the curve \(x e^y+y e^x=4\) at the point (0, 4) is \(y=-(4+e^4) x+4\).
What is tangent?A tangent is described as a line that intersects a circle or an ellipse only at one point. If a line touches a curve at P, the point "P" is known as the point of tangency.
Now according to the question;
To obtain the tangent at a given point, we must first obtain the slope at that point by obtaining the differentiation value at that point \(\left.y^{\prime}\right|_{x=0, y=4}\) as-
Consider the given equation;
\(x e^y+y e^x=4\)
Differentiate both side with respect to x;
\(\begin{aligned}&\frac{d}{d x}\left(x e^y+y e^x\right)=\frac{d}{d x} 4 \\&\frac{d}{d x} x e^y+\frac{d}{d x} y e^x=0\end{aligned}\)
Now apply product rule;
\(\begin{aligned}&e^y \frac{d}{d x} x+x \frac{d}{d x} e^y+e^x \frac{d}{d x} y+y \frac{d}{d x} e^x=0 \\&e^y \frac{d}{d x} x+x \frac{d}{d y} e^y \cdot y^{\prime}+e^x y^{\prime}+y \frac{d}{d x} e^x=0\end{aligned}\)
Applying exponential and power rule;
\(\begin{aligned}&e^y \cdot 1+x e^y \cdot y^{\prime}+e^x y^{\prime}+y e^x=0 \\&\left(x e^y+e^x\right) y^{\prime}=-y e^x-e^y\end{aligned}\)
Solve the value of y'
\(y^{\prime}=\frac{-y e^x-e^y}{x e^y+e^x}\)
Now, find the value of slope m.
\(m=\left.y^{\prime}\right|_{x=0, y=4}\)
\(\frac{-4 \cdot e^0-e^4}{0 e^4+e^0}=-4-e^4\)
Now, using the point-slope formula, obtain the line equation as follows.
\(\begin{aligned}&\left(y-y_1\right)=m\left(x-x_1\right) \\&(y-4)=-(4+e^4) \cdot(x-0) \\&y=-(4+e^4) x+4\end{aligned}\)
Therefore, an equation of the tangent line to the curve is \(y=-(4+e^4) x+4\).
To know more about the tangent line, here
https://brainly.com/question/6617153
#SPJ4
Part of the population of 7,000 elk at a wildlife preserve is infected with a parasite. A random sample of 50 elk shows that 7 of them are infected. How many elk are likely to be infected?
Answers
Answer:
620
Explanation:
When the sample is given, the number of elk are likely to be infected is to be considered as the 620.
Calculation of the number of elk:
Since the population is 7,750.
The random sample is 50.
So here be like
= 620
hence, When the sample is given, the number of elk are likely to be infected is to be considered as the 620.
You are going to invest $5000 at 6.5% compounded quarterly. How much money will you have after 10 years? (remember to round money to 2 decimal places)
Answers
Answer:
Below
Step-by-step explanation:
Formula : FV = PV ( 1 + i)^n <====you just have to LEARN/KNOW this
FV = future value = ? PV = present value = 5000
Periods per year 4 n = periods = 40
interest per period in decimal form .065/5
Plug in the values :
FV = 5000 (1 + .065/4)^40 = 9527.79 dollars
How Many texts?please help.

Answers
Answer:
176
Step-by-step explanation:
91/9.10=0.10
17.60/0.10=176
Answer:
176
Step-by-step explanation:
A recipe calls for 3 3/ 5 cups of kidney beans and 2 2/3 cups of diced tomatoes. if the recipe is multiplied by 2 1/2, how much of the mixture will there be?
Answers
Answer:
There will be 15 2/3 cups in the mixture.
Step-by-step explanation:
3 3/5 + 2 2/3 = 3 9/15 + 2 10/15 = 5 19/15
= 6 4/15
6 4/15 × 2 1/2 = 94/15 × 5/2 = 47/3 = 15 2/3
So there will be 15 2/3 cups in the mixture.
line c and d are perpendicular. the slope of line c is -2/3. which equation is true?

Answers
Answer:
The slope of line d is 3/2 since the slopes of perpendicular lines are negative reciprocals of each other.
So the correct equation is
-2/3 × slope of d = -1
Answer:
3/2
Step-by-step explanation:
If a line is perpendicular to the other it's slope is the inverse reciprocal of the other slope
On a toll road, there are 7 lanes for drivers to pay their toll. Customer arrival times are random, with an exponential distribution. Service times are random, with an exponential distribution. What is the proper description for this queueing system.
Answers
Queueing system can be analyzed using queueing theory to determine performance measures such as the average queue length, average waiting time, and utilization of the service channels.
The queueing system you have described can be modeled as an M/M/7 queue, where:
M represents that inter-arrival times and service times are exponentially distributed.
M represents that the arrival process is memoryless, meaning that the probability of a customer arriving at any given time does not depend on the previous arrival times or the state of the system.
7 represents the number of service channels, or lanes, available for customers to pay their toll.
The notation for this system is M/M/7, which indicates that it has an infinite queue capacity and that there is no limit to the number of customers that can be waiting in the queue.
In this queueing system, customers arrive randomly and independently, and they join the queue if all lanes are busy. They are served on a first-come, first-served basis, with the service times also being exponentially distributed.
This queueing system can be analyzed using queueing theory to determine performance measures such as the average queue length, average waiting time, and utilization of the service channels.
for such more question on Queueing system
https://brainly.com/question/16332322
#SPJ11
Please help due soon!

Answers
h(t)=6 for 7 ≤ t ≤ 8
please i’m really struggling with this :((
Answers
Answer:
thn 6<7<8 is your answer