A researcher measures eye color for a sample of n = 50 people. which measure of central tendency would be appropriate to summarize the measurements?
Answers
According to the statement:
Mode measure of central tendency would be appropriate to summarize the measurements.
The correct option is B.
Briefing:We can't use mean or median because they have no physical meaning, i.e., eyes that are somewhere between black and white.
When you need to use all of the data's values, you would use the mean. When you only need to use two values, such as the upper and lower values, you would use the median. And when ones data is unobservable, such as when you need to determine peoples' opinions, you would use the mode.
What is mean ,Midian and mode?Add up all the values inside the data set, then divide by the total number of values to find the mean. List the data set's values in numerical order, and then find the value that sits in the middle of the list to determine the median. Choose the data set value that appears the most frequently to determine the mode.
To know more about mode visit:
https://brainly.com/question/17727138
#SPJ4
I understand that the question you are looking for is:
A researcher measures eye color for a sample of n = 50 people. Which measure of central tendency would be appropriate to summarize the measurements?
Select one:
a. weighted mean
b. mode
c. median
d. mean
Related Questions
You are given the point (1, π/2) in polar coordinates. (i) Find another pair of polar coordinates for this point such that r > 0 and 2π < θ < 4π. (ii) Find another pair of polar coordinates for this point such that r < 0 and 0 < θ < 2π (b) You are given the point (-2, π/4) in polar coordinates. (i) Find another pair of polar coordinates for this point such that r > 0 and 2π < θ < 4π. (ii) Find another pair of polar coordinates for this point such that r < 0 and-2x < θ < 0. r2 (c) You are given the point (3,2) in polar coordinates. (i) Find another pair of polar coordinates for this point such that r > 0 and 2π < θ < 4T. (ii) Find another pair of polar coordinates for this point such that r < 0 and 0 θ < 2π.
Answers
The new pair of polar Coordinates for the given point is (-3, 2π + 2).
(a) Given point (1, π/2) in polar coordinates, we can find another pair of polar coordinates such that r > 0 and 2π < θ < 4π as follows:
Let us add 2π to the given θ to get a new value greater than 2π. So, θ' = π/2 + 2π = 5π/2.
Therefore, the new pair of polar coordinates for the given point is (1, 5π/2).
To find another pair of polar coordinates such that r < 0 and 0 < θ < 2π, we can use the fact that adding or subtracting any multiple of 2π from θ does not change the point represented by the polar coordinates. So, we can subtract 2π from the given θ to get a new value between 0 and 2π. Thus, θ'' = π/2 - 2π = -3π/2.
Therefore, the new pair of polar coordinates for the given point is (-1, -3π/2).
(b) Given point (-2, π/4) in polar coordinates, we can find another pair of polar coordinates such that r > 0 and 2π < θ < 4π as follows:
Let us add 2π to the given θ to get a new value greater than 2π. So, θ' = π/4 + 2π = 9π/4.
Therefore, the new pair of polar coordinates for the given point is (2, 9π/4).
To find another pair of polar coordinates such that r < 0 and -2π < θ < 0, we can subtract π from the given θ to get a new value between -π and 0. Thus, θ'' = π/4 - π = -3π/4.
Therefore, the new pair of polar coordinates for the given point is (-2, -3π/4).
(c) Given point (3,2) in polar coordinates, we can find another pair of polar coordinates such that r > 0 and 2π < θ < 4π as follows:
Let us add 2π to the given θ to get a new value greater than 2π. So, θ' = 2 + 2π = 2π + 2.
Therefore, the new pair of polar coordinates for the given point is (3, 2π + 2).
To find another pair of polar coordinates such that r < 0 and 0 < θ < 2π, we can use the fact that adding or subtracting any multiple of 2π from θ does not change the point represented by the polar coordinates. So, we can add 2π to the given θ to get a new value between 2π and 4π. Thus, θ'' = 2 + 2π = 2π + 2.
Therefore, the new pair of polar coordinates for the given point is (-3, 2π + 2).
To Learn More About Coordinates
https://brainly.com/question/31092015
#SPJ11
If the area of the trapezoid below is 75 square units, what is the value of x?
A. 12 units
B. 6 units
C. 1.5 units
D 3 units

Answers
Answer:
area of trapezoid= 1/2 × ( a + b ) × high
75cm² = 1/2 × (8+17) × h
75. = 1/2 × 25 × h
75. = 12,5 × h
75. = 12,5h
h = 75 ÷ 12,5
h. = 6 ( B )
A cyclist is riding on a bike trail, pedaling at a speed of 20 miles per hour. the cyclist plans to pedal at this speed for the next 35 miles, plus or minus 10 miles. find the minimum and maximum number of hours the cyclist will pedal at that speed.
Answers
The cyclist will pedal at given speed for minimum 1.25 and maximum 2.25 hours.
The relation between speed, distance and time is as follows -
Speed = distance ÷ time. The maximum and minimum number of hours will depend on the distance. The maximum number of hours will be spent when maximum distance is covered, and minimum number of hours will be spent when minimum distance is covered.
Maximum distance = 35 + 10
Maximum distance = 45 miles
Minimum distance = 35 - 10
Minimum distance = 25 miles
Maximum number of hours = 45 ÷ 20
Maximum number of hours = 2.25 hours
Minimum number of hours = 25 ÷ 20
Minimum number of hours = 1.25 hours
Thus, cyclist will pedal at given speed for minimum 1.25 and maximum 2.25 hours.
Learn more about calculations on maximum and minimum -
https://brainly.com/question/24866444
#SPJ4
Are all equilateral triangles congruent Why?
Answers
For a triangle to be equilateral all its angle should be same which is 60° but for them to be congruent their sides should also be same in measure.
Therefore two equilateral triangles are not always congruent with one another as because there can be difference in the measure of their sides.
The sum of angles of a triangle is 180 degree which is the sum of angles of the triangle's three angles.
There are three types of triangles based on different aspects .
Based on the lengths of their sides, triangles can be classified as
ScaleneIsoscelesEquilateralAs in an equilateral triangle all of the sides are of the same length. and all the angle measure will be 60 degrees. An equilateral triangle is also known as an equiangular triangle since its angles are all the same.
To learn more about triangles
brainly.com/question/2773823
#SPJ4
find the expectation value of the position squared when the particle in the box is in its third excited state. answer this question with the correct coefficient of l2 for the expectation value.
Answers
The expectation value of the position squared when the particle in the box is in its third excited state is equal to \(\frac{9l^2}{8}\), where l is the length of the box. This is equal to nine-eighths of the length of the box squared.
The expectation value of the position squared when the particle in the box is in its third excited state can be calculated using the formula\(\langle x^2 \rangle = \frac{l^2}{8} \left( 2n^2 + 6n + 3 \right)\),
where n is the quantum number of the state and l is the length of the box. Here, n is 3, so the expectation value is equal to
\(\frac{l^2}{8} \left( 2 \times 3^2 + 6 \times 3 + 3 \right) = \frac{9l^2}{8}\).
This can be written as nine-eighths of the length of the box squared.
Learn more about value here
https://brainly.com/question/13799105
#SPJ4
Use the Left and Right Riemann Sums with 3 rectangles to estimate the area under the curve of y=lnx on the interval of [2,9]. Round your answers to the second decimal place.

Answers
Rieman sums are used to calculate the approximate value of the area under the curve of real functions.
A left Riemann sum uses rectangles whose top-left vertices are on the curve while the right Riemann sum uses rectangles whose top-right vertices are on the curve.
The width of each rectangle is given by:
\(w=\frac{b-a}{n}\)Where a and b are the endpoints of the interval and n is the number of rectangles.
We are given the function:
y = ln x on the interval [2, 9]
And it's required to use n = 3 rectangles, thus:
\(w=\frac{9-2}{3}=2.333\)For the left Riemann sum, we need to calculate the values of y for:
x = 2
x = 2 + w = 4.333
x = 2 + 2w = 6.667
f(2) = ln 2 = 0.6931
f(4.333) = 1.4662
f(6.667) = 1.8972
The area of the rectangles is the height by the base:
A = 0.6931 x 2.333 + 1.4662 x 2.333 + 1.8972 x 2.333
A = 9.4640
For the right Rieman sum, we need to calculate the values of y for:
x = 2 + w = 4.333
x = 2 + 2w = 6.667
x = 2 + 3w = 9
f(4.333) = 1.4662
f(6.667) = 1.8972
f(9)= 2.1972
Calculate the area of the rectangles:
A = 1.4662 x 2.333 + 1.8972 x 2.333 + 2.1972 x 2.333
A = 12.973
Note: The real value for the area (using integration) is 11.39
Find the interval in which the function is positive.
f(x)=x²-7x + 10
1. (-∞0, 2)
II. (2,5)
III. (5,00)
O I, II
O I, III
O II, III
O II only

Answers
Answer:
(b) I, III
Step-by-step explanation:
The correct answer can be chosen based on your knowledge of the shape of the graph of f(x).
General shapeThe leading coefficient of this quadratic function being positive tells you the graph will be a parabola that opens upward. The left branch of the parabola will extend to positive infinity, as will the right branch.
If there are x-intercepts, the x-values between those will be where the graph has crossed the x-axis and function values are negative.
Specific shapeThe answer choices suggest that x=2 and x=5 are x-intercepts of the function's graph. These can be checked, if you like, by evaluating f(2) and f(5).
f(2) = 2² -7·2 +10 = 4 -14 +10 = 0
f(5) = 5² -7·5 +10 = 25 -35 +10 = 0
This means the function will be positive for x < 2 and for x > 5. These intervals are described by I and III.

let a be a m × n real matrix. let x be a n × 1 column vector, and y be a m × 1 column vector. prove that ⟨ax, y⟩
Answers
The expression ⟨ax, y⟩ represents the inner product (also known as dot product) between the column vector ax and the column vector y. To prove this, we can expand the inner product using matrix and vector operations.
First, let's write the given matrix equation explicitly. We have:
ax = [a1x1 + a2x2 + ... + anx_n]
where a1, a2, ..., an are the columns of matrix a, and x1, x2, ..., xn are the elements of vector x.
Expanding the inner product, we get:
⟨ax, y⟩ = ⟨[a1x1 + a2x2 + ... + anx_n], y⟩
Using the linearity of the inner product, we can distribute it over the addition:
⟨ax, y⟩ = ⟨a1x1, y⟩ + ⟨a2x2, y⟩ + ... + ⟨anx_n, y⟩
Now, let's focus on one term ⟨aixi, y⟩ for some i (1 ≤ i ≤ n). We can apply the properties of the inner product:
⟨aixi, y⟩ = (aixi)ᵀy
Expanding the transpose and using matrix and vector operations, we have:
(aixi)ᵀy = (xiᵀaiᵀ)y = xiᵀ(aiᵀy)
Recall that aiᵀ is the transpose of the ith column of matrix a. Thus, we can rewrite the expression as:
xiᵀ(aiᵀy) = (xiᵀaiᵀ)y = ⟨xi, aiᵀy⟩
Therefore, we can rewrite the original inner product as:
⟨ax, y⟩ = ⟨a1x1, y⟩ + ⟨a2x2, y⟩ + ... + ⟨anx_n, y⟩ = ⟨x1, a1ᵀy⟩ + ⟨x2, a2ᵀy⟩ + ... + ⟨xn, anᵀy⟩
So, we have shown that ⟨ax, y⟩ is equal to the sum of the inner products between each component of vector x and the transpose of the corresponding column of matrix a multiplied by vector y.
Learn more about matrix here:
brainly.com/question/28180105
#SPJ11
8x - 3 /AX 4x + 3 When angles form a linear pair, their sum is 180°. 8x - 3+ 4x + 3 = 180 [?]x + [] = 180
![8x - 3 /AX 4x + 3 When angles form a linear pair, their sum is 180. 8x - 3+ 4x + 3 = 180 [?]x + [] =](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/qyHHRwzU1NH60DvaXnSWaKqNVEUte8Mf.jpeg)
Answers
Answer:
12x + 0 = 180x = 15Step-by-step explanation:
You are given the equation 8x -3 +4x +3 = 180 and asked to simplify it and solve for x.
SimplifiedCollecting terms, we have ...
(8 +4)x +(-3 +3) = 180
12x + 0 = 180
Dividing by the coefficient of x gives ...
x = 180/12 = 15
The value of x is 15.
Why is a normal distribution "normal"?
Answers
Step-by-step explanation:
Normal distribution, also known as the Gaussian distribution, is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean.
Angle
x
= 076° and angle
y
= 111°.
Find the bearing of point A from point O.
Answers
The bearing of point A from point O is 256°.
What are bearings?In mathematics, a bearing is the angle in degrees measured clockwise from north. Bearings are usually given as a three-figure bearing. For example, 30° clockwise from north is usually written as 030°.
Given that, angle x= 076° and angle y = 111°.
Now, the bearing of point A from point O is
180°+ 076°
= 256°
Therefore, the bearing of point A from point O is 256°.
Learn more about the bearings here:
https://brainly.com/question/27962362.
#SPJ1

Y 35(0.57)
What is the growth or decay factor
Answers
Answer:
decay factor is 0.43
Step-by-step explanation:
1-0.57=0.43
HELP ASAP PLEASE
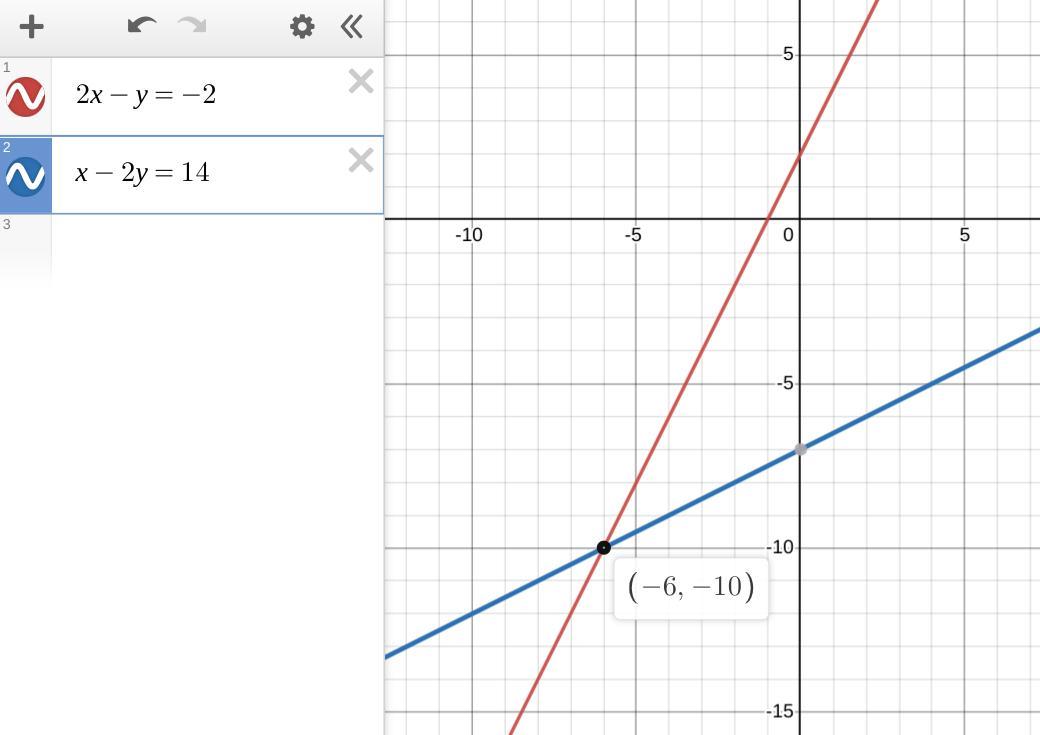
Given the system of equations:
2x − y = −2
x= 14 + 2y
What is the value of the system determinant?
What is the value of the y−determinant?
What is the value of the x−determinant?
What is the solution to the system of equations?
Show all of your work.
Answers
Answer:
solution: (x, y) = (-6, -10)
(see below for the "work")
Step-by-step explanation:
You are asked for the solution following the steps of evaluating Cramer's Rule.
System of equations in matrix formSubtracting 2y from the second equation puts it in standard form, so the system is ...
2x -y = -2x -2y = 14Then the matrix equation is ...
\(\mathbf{AX}=\mathbf{B}\\\\\left[\begin{array}{cc}2&-1\\1&-2\end{array}\right] \left[\begin{array}{c}x\\y\end{array}\right] =\left[\begin{array}{c}-2\\14\end{array}\right]\)
DeterminantThe system determinant (Δ) is the determinant of the matrix of the coefficients of the variables.
\(\left|\begin{array}{cc}2&-1\\1&-2\end{array}\right|=(2)(-2)-(1)(-1)=-4+1=\boxed{-3}\)
Y-determinantThe y-determinant (Δy) is the determinant of the matrix with the y-coefficients replaced by the constants (B).
\(\left|\begin{array}{cc}2&-2\\1&14\end{array}\right|=(2)(14)-(1)(-2)=28+2=\boxed{30}\)
X-determinantThe x-determinant (Δx) is the determinant of the matrix with the x-coefficients replaced by the constants (B).
\(\left|\begin{array}{cc}-2&-1\\14&-2\end{array}\right|=(-2)(-2)-(14)(-1)=4+14=\boxed{18}\)
SolutionThe solution is the ratio of the appropriate determinants:
x = Δx/Δ = 18/-3 = -6
y = Δy/Δ = 30/-3 = -10
The solution is (x, y) = (-6, -10).
__
The attachment shows a matching graphical solution.
Part of a bus timetable is shown below.
The average speed of the bus between Hawkes Meadow and Brunswick Street is
29 km/h.
Work out how many kilometres the bus travels between these two stops.
If your answer is a decimal, give it to 1 d.p.
Bus stop
Hawkes Meadow
Othello Avenue
Brunswick Street
Kingsway
Parish Church
Upper Parade
Time
14:25
14:32
14:40
14:46
14:51
14:55

Answers
Hence, the distance between Hawkes Meadow and Brunswick Street is roughly 11.1 kilometres (km).
what is distance ?Distance is a unit used to express the distances between two objects or positions. This is a scalar value that is typically stated in length units like feet, metres, kilometres, or miles. Distance between two things is a physical concept that specifies their separation; it is frequently used to estimate how much space there is between them. The shortest distance, also referred to as "as the crow flies," can be calculated either along a horizontal path or a curved path. Displacement, or the shift in an object's position from its original location to its end position, is a notion in physics that is closely connected to distance.
given
Using the data from the timetable and the calculation, we can determine how many kilometres the bus travels between Hawkes Meadow and Brunswick Street:
Distance is determined by multiplying time and speed.
According to the timetable, the bus travels from Hawkes Meadow to Othello Avenue in 15 minutes (from 14:25 to 14:32), and from Othello Avenue to Brunswick Street in 8 more minutes (i.e., from 14:32 to 14:40). Hence, it takes 15 + 8 = 23 minutes to get from Hawkes Meadow to Brunswick Street.
Also, we are informed that the bus travels at an average speed of 29 km/h between Hawkes Meadow and Brunswick Street.
To utilise the calculation, we must first divide the time in minutes by 60 to convert it to hours:
23, divided by 60 hours, or 0.3833 hours (rounded to 4 decimal places)
Hence, we can compute the distance using the following formula:
11.12 kilometres is equal to 29 km/h times 0.3833 hours (rounded to 2 decimal places)
Hence, the distance between Hawkes Meadow and Brunswick Street is roughly 11.1 kilometres (km).
To know more about distance visit :-
brainly.com/question/29130992
#SPJ1
pls help
What is the value of x?
Enter your answer in the box.
x =

Answers
Answer:
54
Step-by-step explanation:
Since these two angles are vertical angles, they must be congruent. Therefore we can set up the following equation:
2x+2=3x-52
Subtract 2x from both sides:
2=x-52
x=54
Answer:
x = 54
Step-by-step explanation:
The angles are vertically opposite and are congruent , so
3x - 52 = 2x + 2 ( subtract 2x from both sides )
x - 52 = 2 ( add 52 to both sides )
x = 54
solve 58÷4(6×9)+7(7×3)
Answers
58/4x54+7x21 =
783+7x21 =
783+147 =
930
Answer:
answers 930 ok I hope it help
pls help if you can asap!!!!

Answers
Answer: A
Step-by-step explanation: I would say A because the angle is greater than 90 degrees
Answer:
We have supplementary angles.
76 + 3x + 2 = 180
3x + 78 = 180
3x = 102
x = 34
PLEASE! I NEED MAJOR HELP!!
Select the equation that is in Standard Form:
1.) 9x + 5y = 8
2.)9y = 5x + 8
3.)y = 9r + 5
Answers
Answer:
3.
Step-by-step explanation:
standard form: y=mx+b
Choose the statement that best defines the term "experiment" in the context of probability.a) A process that leads to only one of several possible outcomes.b) A random trial whose outcome can be predicted on the basis of mathematical analysis.c) A process that may or may not confirm a hypothesis.
Answers
The statement that best defines the term "experiment" in the context of probability is (a) "A process that leads to only one of several possible outcomes."
An experiment is a process that is carried out to observe and study the outcome of an event or phenomenon. In probability, an experiment refers to a process that can have multiple outcomes, and the outcome cannot be predicted with certainty before the experiment is carried out.
For example, rolling a dice is an experiment in probability since it has multiple possible outcomes (rolling a 1, 2, 3, 4, 5, or 6) and the outcome cannot be predicted with certainty. Similarly, flipping a coin is also an experiment in probability since it can have two possible outcomes (heads or tails) and the outcome cannot be predicted with certainty.
On the other hand, option (b) is incorrect since a random trial whose outcome can be predicted on the basis of mathematical analysis is not an experiment but a deterministic process. Option (c) is also incorrect since a process that may or may not confirm a hypothesis does not define an experiment in the context of probability.
Learn more about probability here brainly.com/question/30034780
#SPJ4
HELP ME QUICK I AM STUCK ON THIS PROBLEM

Answers
Answer:
3
Step-by-step explanation:
5<18 is 23 and 23 by 6 is 4 and 4 by 2 is 2 + 1 = 3
Which of the following relations is a function?
A. (5, 10), (-9, 3), (-1, 8), (-1,-6)
B. (10,5), (3, -9), (8,-1), (10,-6)
C. (-1, 10),(-9, 3), (-1, 8), (-9,-6)
D. (5, 10).(-9,3), (-1,8), (-6, 10)
Answers
A farmer goes to the market to sell a box of eggs. A clumsy horse steps on the box of eggs and breaks a lot of them. The horse’s rider offers to pay for all of the eggs in the box and asks the farmer how many eggs there were. The farmer does not remember the exact number, but when she took them out of the box two at a time, there was 1 egg left. The same thing happened when she took them out three, four, five and six eggs at a time, but when she took them out 7 at a time, there were no eggs left
Answers
The smallest number of eggs that could have been in the box is 1134
The problem is to find the smallest number of eggs that could have been in the box, given the remainder when taking them out by different numbers. Here are the moves toward tackling it:
Allow n to be the quantity of eggs in the container. Then we have the accompanying arrangement of congruences:
n ≡ 1 (mod 2)
n ≡ 1 (mod 3)
n ≡ 1 (mod 4)
n ≡ 1 (mod 5)
n ≡ 1 (mod 6)
n ≡ 0 (mod 7)
For this problem, we have k = 6 k = 6, a i = {1,1,1,1,1,0} a_i = {1,1,1,1,1,0}, M i = {1260,840,630,504,420,720} M_i = {1260,840,630,504,420,720}, and y i = {−1,−2,−3,-4,-5,-6} y_i = {-1,-2,-3,-4,-5,-6}.
Plugging these values into the formula and simplifying modulo 5040, we get:
n = (−1260 + −1680 + −1890 + −2016 + −2100 + 0) mod 5040
n = (−8946) mod 5040
n = (−3906) mod 5040
n = 1134 mod 5040
Therefore, the smallest number of eggs that could have been in the box is 1134
to know more about congruences click here:
https://brainly.com/question/30818154
#SPJ4
Which of the following is the parent function of all absolute value functions?
A. f(x) = 3x
B. f(x) = (x1
C. f(x) = 21x1
D. fx) = x²
will mark brainlyest!!!! 53:50
Answers
Answer: f(x) =x^2 in other words, D
Sandy uses three and one half pounds of clay to make 7 small vases. Use a proportion to find how many pounds of clay she will use to make 21 small vases.
Answers
Answer: 10.5 pounds of clay
Step-by-step explanation:
We know she uses three and one-half pounds of clay to make seven small vases.
3 1/2 = 3.5
21 is 3 times 7
So We take 3.5 times 3 = 10.5 pounds of clay
she will use 10.5 pounds of clay to make 21 small vases.
The expression 3x + 5x - 5y + 2 consists of four_____.
(hint: these are parts of the expression that are "added or subtracted")
A Factors
B Terms
C Variables
D Coefficients
Answers
Find the Laplace transform of the following functions: (a) t cos tu (t)
Answers
The Laplace transform of the function \(\(f(t) = t \cos(tu)\) ,\(F(s) = -\frac{1}{s(s^2 + u^2)}\).\)
The Laplace transform of a function \(f(t)\) is given by the formula:
\(\[F(s) = \mathcal{L}\{f(t)\} = \int_0^\infty e^{-st} f(t) dt\]\)
Let's proceed with the calculation:
\(\[F(s) = \int_0^\infty e^{-st} (t \cos(tu)) dt\]\)
We can split the integral into two parts using the linearity property of the Laplace transform:
\(\[F(s) = \int_0^\infty e^{-st} t \cos(tu) dt = \int_0^\infty t \cos(tu) e^{-st} dt\]\)
Applying integration by parts:
\(\[F(s) = \left[t \left(\frac{1}{u} \sin(tu) e^{-st}\right)\right]_0^\infty - \int_0^\infty \left(\frac{1}{u} \sin(tu) e^{-st}\right) dt\]\)
The first term evaluates to 0 when evaluated at both limits:
\(\[\left[t \left(\frac{1}{u} \sin(tu) e^{-st}\right)\right]_0^\infty = 0 - 0 = 0\]\)
So, we are left with:
\(\[F(s) = -\int_0^\infty \left(\frac{1}{u} \sin(tu) e^{-st}\right) dt\]\)
To solve the remaining integral, we can use the Laplace transform of the sine function and the convolution property of Laplace transforms.
The Laplace transform of the sine function is given by:
\(\[\mathcal{L}\{\sin(at)\} = \frac{a}{s^2 + a^2}\]\)
In our case, a = u and s is the complex parameter.
Using the convolution property, we can write the remaining integral as:
\(\[F(s) = -\frac{1}{u} \mathcal{L}\{\sin(tu)\} \cdot \mathcal{L}\{e^{-st}\}\]\)
Plugging in the Laplace transform of the sine function and the Laplace transform of the exponential function, we get:
\(\[F(s) = -\frac{1}{u} \cdot \frac{u}{s^2 + u^2} \cdot \frac{1}{s}\]\)
Therefore, the Laplace transform of the function \(\(f(t) = t \cos(tu)\) ,\(F(s) = -\frac{1}{s(s^2 + u^2)}\).\)
Learn more about Laplace Transformation here:
https://brainly.com/question/32625911
#SPJ4
If A is an invertible nxn matrix, then the equation Ax=b is consistent for each b in R". O A. False; the matrix A satisfies Ax=b if and only if A is row equivalent to the identity matrix, and not every matrix that is row equivalent to the identity matrix is invertible. OB. True; since A is invertible, A-1b exists for all b in R" Define x=A-1b. Then Ax = b. OC. True; since A is invertible, A-'b= x for all x in R". Multiply both sides by A and the result is Ax = b. OD. False; the matrix A is invertible if and only if A is row equivalent to the identity matrix, and not every matrix A satisfying Ax=b is row equivalent to the identity matrix.
Answers
Statement is true: If A is an invertible nxn matrix, then the equation\(Ax=b\) is consistent for each b in R. The correct option is (B).Why is it true?Proof: Suppose A is an invertible nxn matrix.
Let b be any vector in R. Since A is invertible, it has an inverse matrix A-1. Then, A-1b exists.Now, define\(x=A-1b\). Then we can write\(b=Ax\). We have shown that a solution x exists for each b. To show that this solution is unique, suppose x1 and x2 both satisfy\(Ax=b\). Then\(Ax1=Ax2=b, and so A(x1 - x2)=0\). Since A is invertible, it has a trivial nullspace.
Thus,\(x1 - x2=0\), and hence x1=x2. Therefore, the solution to \(Ax=b\) is unique. Since the solution exists for every b, the system \(Ax=b\) is consistent for every b. Therefore, the statement is true.Hence, option (B) is correct.
To know more about matrix visit:
https://brainly.com/question/29132693
#SPJ11
The given family of functions is the general solution of the differential equation on the indicated interval. Find a member of the family that is a solution of the initial-value problem. y = c1ex + c2e−x, (−[infinity], [infinity]); y'' − y = 0, y(0) = 0, y'(0) = 5
Answers
The given family of functions is y = c1ex + c2e−x which is the general solution of the differential equation y'' − y = 0 on the indicated interval which is (−∞, ∞).
Now, we are required to find a member of the family that is a solution to the initial-value problem which is
y(0) = 0 and y′(0) = 5.
The differential equation is y'' − y = 0
The characteristic equation is r2 − 1 = 0r2 = 1r1 = 1 and r2 = −1
The general solution of the differential equation is y = c1ex + c2e−x
Let us solve for the constants by using the given initial conditions:
At x = 0,y(0) = c1e0 + c2e0 = 0 + 0 = 0y(0) = 0
means c1 + c2 = 0or c1 = -c2At x = 0, y′(0) = c1ex |x=0 + c2e−x |x=0(d/dx)(c1ex + c2e−x) |x=0y′(0) = c1 - c2 = 5c1 - c2 = 5c1 - (-c1) = 5c1 + c1 = 5c1 = 5/2c1 = 5/2
Let's replace c1 = 5/2 in c1 = -c2, c2 = -5/2
The solution of the initial-value problem y = (5/2)ex − (5/2)e−x is a member of the family y = c1ex + c2e−x that is a solution of the initial-value problem y(0) = 0 and y′(0) = 5.
#SPJ11
Learn more about differential equations at: https://brainly.com/question/1164377
Which statement about the transformation is true? it is rigid because all side lengths and angles are congruent. It is rigid because no side lengths or angles are congruent. It is nonrigid because all side lengths are congruent. It is nonrigid because no side lengths or angles are congruent.
Answers
The statement "It is rigid because all side lengths and angles are congruent" is true.
In mathematics, a transformation is considered rigid if it preserves distances and angles. For example, a translation, rotation, or reflection is a rigid transformation because it preserves distances and angles. If a transformation preserves side lengths and angles, then it is considered rigid, regardless of whether the side lengths and angles are congruent or not.
Answer: A. it is rigid because all side lengths and angles are congruent.
Step-by-step explanation: RIGHT ON EDGE 2023
Examine the expanded form. A ∙ a ∙ a ∙ a ∙ a ∙ a ∙ a Which is the expression in exponential form? 7a 7a a7 a 7.