a random sample of size 36 is taken from a population with mean 17 and standard deviation 6. the probability that the sample mean is greater than 18 is?

Answer:

right angle

Step-by-step explanation:

Answer:a,b, and d

Step-by-step explanation:

Answer:

V = 396 cubic inches

Step-by-step explanation:

width = w; length = l; height = h; volume = V; area of smallest face = a

base units are inches

w = 2 + l

h = l - 5

Height is smallest and length is second smallest (h = l -, l = l, w = l +), so a is for h and l.

a = h × l = (l - 5) × l

36 = l^2 - 5l ==> l^2 - 5l - 36 = 0

Factor ==> (l - 9) × (l + 4) = 0

l = 9 and l = -4

Since length cannot be negative, 9 is the only Real answer.

l = 9

h = l - 5 = 9 - 5 = 4

w = 2 + l = 2 + 9 = 11

Volume of rectangular prism/box is length times width times height.

V = l × w × h = 9 × 11 × 4 = 396

The volume of the box with the given dimensions is;

Volume = 396 in³

Let us denote the properties of the box as follows;

Length of box = l

Width of box = w

Height of box = h

Area of the smallest face of box = a  

We are told that the width is 2 inches more than the length. Thus;

w = 2 + l

We are told that the height is 5 inches less than its length. Thus;

h = l - 5

Since length is smaller than width but bigger than height, the height and length are the 2 smallest faces

Thus,

a = h × l

plugging in the relevant values gives;

a = (l - 5) × l

a = l² - 5l

We are told that the area of the two smallest faces is 36 in². Thus;

l² - 5l = 36

l² - 5l - 36 = 0

Using online quadratic equation solver, we have; l = 9 inches

Plugging in 9 for h in; h = l - 5  

h = 9 - 5

h = 4

Also, plugging in 9 for l into; w = 2 + l, we have;

w = 2 + 9

w = 11

Volume of box is given by;

Volume = length × width × height

Volume = 9 × 11 × 4

Volume = 396 in³

Read more at;https://brainly.com/question/13973603

Complete question :

Suppose you know that the prices paid for cars are normally distributed with a MEAN or $17,000 and a STANDARD DEVIATION of $500. Use the EMPIRICAL RULE to find the percentage of buyers who paid between 15500 and 17000

Answer:

49.85%

Step-by-step explanation:

Mean = 17000

Standard deviation = 500

Obtain the Z score, which is the number of standard deviations from the mean :

((17000 - 17000) / 500) = 0

((15500 - 17000) / 500) = - 3

-3 to 3 = (3 standard deviations)

However,

The value here is (-3 to 0) ; which is only 3 standard deviations to the left.

3 standard deviation = 99.7% (empirical rule)

Since it is only (-3 to 0) ; which is only 3 standard deviations to the left. ; the percentage will be halved

99.7% / 2 = 49.85%

Hence, percentage of buyers who paid between 15500 and 17000 is 49.85%

Answer:

Reflections across the line y = x

A reflection across the line y = x switches the x and y-coordinates of all the points in a figure such that (x, y) becomes (y, x). Triangle ABC is reflected across the line y = x to form triangle DEF. Triangle ABC has vertices A (-2, 2), B (-6, 5) and C (-3, 6).

The vector space that has exactly one basis is the trivial vector space, which is the vector space containing only the zero vector.

A basis for a vector space is a set of linearly independent vectors that span the entire space. In a non-trivial vector space (a space that contains more than just the zero vector), there are infinitely many possible bases. This is because any set of linearly independent vectors that span the space can be used as a basis.

However, in the trivial vector space, there is only one vector (the zero vector), and it is linearly independent of itself. Therefore, the trivial vector space has exactly one basis, which is the set containing only the zero vector. Any other set of vectors in the trivial vector space is linearly dependent, and therefore cannot be used as a basis.

Find out more about trivial vector space,

brainly.com/question/14375935

#SPJ4

Find out more about vector spaces

brainly.com/question/14375935

#SPJ4

The statement, "Colbert "Real-Estate" Agency's number of home showings by its agents is same "each-day" of week, then variable for number of showings, is a continuous distribution" is False, because it represents a discrete distribution.

If the Colbert "Real-Estate" Agency has determined the number of "home-showings" by their agents is "same" each day of week, then variable "number of showings" is not a continuous distribution. Rather, it is a discrete distribution,

where the values can take on only  finite number of values. In this case, the number of home showings can only be a whole number, such as 0, 1, 2, 3, etc.

A continuous distribution is the one where the possible values of the variable are not restricted to any particular set of numbers, and can include any value in a given range.

An example of a continuous distribution would be the height of adult humans, where any real number between 0 and infinity is a possible value.

Therefore, the statement is False.

Learn more about Distribution here

https://brainly.com/question/30032500

#SPJ4

Answer:9

Step-by-step explanation:

Answer:

try 5 if that is an answer choice. if not then sorry i couldn't help!

Answer:

(5, 1/2)

Step-by-step explanation:

To find the midpoint

Take the sum of the x coordinates and divide by 2

(5+5)/2 = 10/2 = 5

Take the sum of the y coordinates and divide by 2

(4+-3)/2 = 1/2 = 1/2

The midpoint is ( 5, 1/2)

It is answer D

Its is exactly in between these to values

It is proved that Point A is situated equal distance from Triangle PQA and RQA.

It is a line that divide an angle or a line in two equal parts.  In the given figure, QA is a bisector as it divides the angle PQR.

Triangles are called congruent when they have equal corresponding sides and equal corresponding angles. As shown in figure, the bisector QA creates two congruent triangle PQA and RQA.

it is given, QA is bisector of angle Q, so point A lies equal distance from P and R. According to the figure, APQ and ARQ are right angle.

As per the rules of congruence theorem, triangle PQA and Triangle RQA are two congruent triangles.

hence, A is the same distance from P and R

to know more about bisector visit:

https://brainly.com/question/30015103

#SPJ1

Statement                                                                  Reason

1. QA is the bisector of ∠PQR                                   Given

2. ∠PQA   ≅ ∠RQA                                          Definition of bisector

4. ∠QXA ≅ ∠QYA                                   All right angles are congruent

5. QA ≅ QA                                                                Given

6.△PQA ≅ △RQA                                            AAS Postulate

8. Point A is equidistance                              Definition equidistance

from the side of ∠PQR        

What is right triangle?

A right triangle, also known as a right-angled triangle, right-perpendicular triangle, orthogonal triangle, or formerly rectangle triangle, is a triangle with one right angle, or two perpendicular sides. The foundation of trigonometry is the relationship between the sides and various angles of the right triangle.

Given that point A is lie on the bisector of ∠PQR.

When anything is divided into two equal or congruent portions, usually by a line, it is said to have been bisected in geometry. The line is then referred to as the bisector. Segment bisectors and angle bisectors are the sorts of bisectors that are most frequently taken into consideration.

Therefore QA is the bisector of ∠PQR

Then ∠PQA   ≅ ∠RQA  

Since ∠QXA and ∠QYA are right angle, therefore they are congruent.

∠QXA ≅ ∠QYA

QA ≅ QA

AAS postulate: The triangles are congruent if two angles and the excluded side of one triangle match two angles and the excluded side of another triangle.

According to AAS postulate,

△PQA ≅ △RQA  

Point A is equidistance from ∠PQR.

To learn more about CPCT theorem, click on below link:

https://brainly.com/question/18553509

#SPJ1

As S = {f in C[a, b] | f(a) - 2f (b) = 0} is a subspace of C[a, b] or not.

To determine whether S = {f in C[a, b] | f(a) - 2f(b) = 0} is a subspace of the vector space C[a, b] (the set of all continuous real-valued functions defined on a closed interval [a, b]), we must check if it satisfies the following three conditions:

1. The zero vector is in S.
2. S is closed under vector addition.
3. S is closed under scalar multiplication.

1. The zero vector in C[a, b] is the function f(x) = 0 for all x in [a, b]. For this function, f(a) - 2f(b) = 0 - 2(0) = 0, so the zero vector is in S.

2. Let f and g be two functions in S. Then, f(a) - 2f(b) = 0 and g(a) - 2g(b) = 0. We need to check if their sum, (f + g), is also in S. For the sum, we have (f + g)(a) - 2(f + g)(b) = f(a) + g(a) - 2[f(b) + g(b)] = (f(a) - 2f(b)) + (g(a) - 2g(b)) = 0 + 0 = 0. Thus, S is closed under vector addition.

3. Let f be a function in S, and let c be a scalar. We need to check if cf is in S. For the scalar multiplication, we have (cf)(a) - 2(cf)(b) = c[f(a) - 2f(b)] = c(0) = 0. Thus, S is closed under scalar multiplication.

Since S satisfies all three conditions, it is a subspace of the vector space C[a, b] of continuous real-valued functions defined on a closed interval [a, b].

To learn more about subspace: https://brainly.com/question/30215433

#SPJ11

You have a total of six different ways to select a snack and a beverage at the amusement park.

To determine the number of different ways you can select a snack and a beverage, we can use the concept of combinations.

Let's analyze the options:

Snack: You can choose either a chili dog or popcorn. This gives us 2 choices for the snack.

Beverage: You can choose either lemonade, an energy drink, or water. This gives us 3 choices for the beverage.

To calculate the total number of combinations, we multiply the number of choices for the snack by the number of choices for the beverage. Therefore, the number of different ways to select a snack and a beverage is 2 (choices for snack) multiplied by 3 (choices for beverage), which equals 6.

In other words, there are six different combinations possible:

Chili dog and lemonade

Chili dog and energy drink

Chili dog and water

Popcorn and lemonade

Popcorn and energy drink

Popcorn and water

So, when considering all the options, you have a total of six different ways to select a snack and a beverage at the amusement park.

For more question on ways visit:

https://brainly.com/question/30379290

#SPJ8

The ratio 2 gallons to 27 quarts as a fraction in its simplest form is 4/27

The given ratio is:

2 gallons to 27 quarts

This can also be written as:

2 gallons  :  27 quarts

Convert 27 quarts to gallons so that both items in the ratio can be of equal unit

Note that:

1 quart  =  0.25 gallons

27 quarts = 0.25 x 27

27 quarts = 6.75 gallons

The ratio can therefore be re-written as:

2 gallons :  6.75 gallons

In fraction form:

2 gallons  :  27 quarts = 2/6.75

Multiply the numerator and denominator by 4

2 gallons  :  27 quarts  =  4/27

The ratio 2 gallons to 27 quarts as a fraction in its simplest form is 4/27

Learn more here: https://brainly.com/question/25843849

Answer:

50

Step-by-step explanation:

1.25 - .05 = 1.20 made per balloon

60/1.2 = 50 balloons sold to recoup 60$ start up and break even

|z|= 2 √(5), |2z|=4 √(5)  and |3z|=6 √(5).  |2z|= 2|z|  this relationship holds true.

In mathematics, the modulus, also known as the absolute value or magnitude, is a function that returns the positive value of a number regardless of its sign. The modulus function is denoted by the vertical bars surrounding the number or expression, for example, |x| or |a-b|.

The modulus of a number is defined as the distance of that number from zero on the number line. For example, the modulus of 5 is 5, while the modulus of -5 is also 5. This is because both 5 and -5 are located at a distance of 5 units from zero on the number line.

The modulus function can also be used to express the distance between two numbers. For example, the modulus of the difference between two numbers a and b is written as |a-b|. This gives the distance between the two numbers on the number line, regardless of their signs.

We are given that z = 4 - 2i.

The magnitude (absolute value) of a complex number a + bi is given by |a + bi| = √(a² + b²).

Therefore, we have:

|z| = |4 - 2i| = √(4² + (-2)²) = √20) = 2 √(5)

To find |2z| and |3z|, we multiply z by 2 and 3, respectively, and then take the magnitude:

|2z| = |2(4 - 2i)| = |8 - 4i| = √(8² + (-4)²) = √(80) = 4 √(5)

|3z| = |3(4 - 2i)| = |12 - 6i| = √(12² + (-6)²) = √(180) = 6 √(5)

Finally, we can investigate if |2z| = 2|z|:

|2z| = 4 √(5)

2|z| = 2(2 √(5)) = 4 √(5)

Since |2z| = 2|z|, this relationship holds true.

To know more about function visit:

https://brainly.com/question/23712366

#SPJ1  

Answer:

Answer is 2

Step-by-step explanation:

Answer:

1st do you do 6 × 3 to get 18 and then you add that by 4 because parentheses come 1st. You want to use Pemdas so you do 1/2 times 22 and then you want to subtract 9 from 22 to get 12.

Answer:

3

Step-by-step explanation:

5.5 litres paint needed for 1 stool

1  litres paint needed for  1/ 5.5

20 litres paint needed for  20/5.5

= 3.636

And now comes the twist, you can't paint 3.6 stools. also You can't paint 4 stools. You need to round down to 3

Answer:

Step-by-step explanation:

Therefore, the set of points that does not determine a spherical triangle is any set of three non-collinear points that do not lie on a great circle of the sphere.

Explanation: A spherical triangle is a triangle formed on the surface of a sphere by three great circle arcs intersecting pairwise to form three vertices. Any three points that do not lie on a great circle of the sphere will not determine a spherical triangle. Therefore, the set of points that does not determine a spherical triangle is any set of three non-collinear points that do not lie on a great circle of the sphere. Any set of three non-collinear points that do not lie on a great circle of the sphere does not determine a spherical triangle.

Therefore, the set of points that does not determine a spherical triangle is any set of three non-collinear points that do not lie on a great circle of the sphere.

To know more about triangle visit:

https://brainly.com/question/1058720

#SPJ11

Answer:

13 × 10 = 130 ( it's a rectangle)

5² π /2 ≈ 12.5 × 3.14 = 39.25 ( semicircle)

130 + 39.25 = 169.25 ≈ 170

Answer:

x = 12

Step-by-step explanation:

18:24 (comparing the same sides for the similar shapes; 18 and 24) when simplified down is equal to 3:4.

Using this 3:4 scale factor we can find the missing side x.

Solving for x :

\(\frac{3}{4}\) × 16 = 12

x = 12

OR: Set up a proportion:

\(\frac{24}{16}\) × \(\frac{18}{x}\)

cross-multiply

16 × 18 = 288

24 × x = 24x

288 = 24x

x = 12

Answer:

y = -1/3x - 5

Step-by-step explanation:

Use rise over run to find the slope: (y2 - y1) / (x2 - x1)

Plug in the points:

(y2 - y1) / (x2 - x1)

(-7 + 3) / (6 + 6)

-4 / 12

= -1/3

Plug in the slope and a point into y = mx + b, and solve for b:

y = mx + b

-3 = -1/3(-6) + b

-3 = 2 + b

-5 = b

Plug in the slope and b into y = mx + b

y = -1/3x - 5 is the equation of the line

Answer:

m

Step-by-step explanation:

the slope or growth rate of the function is the coefficient of the variable x, which is m in this case

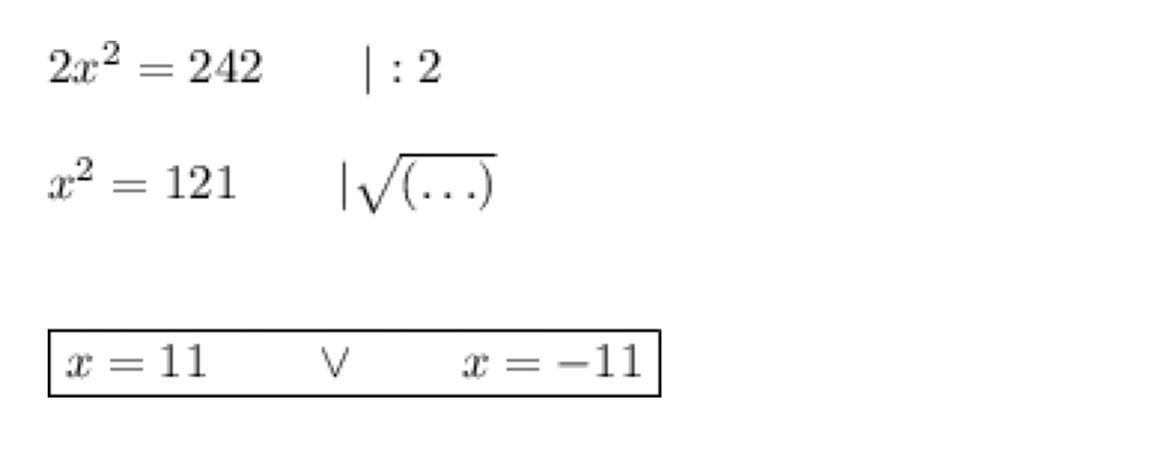
Answer:

\(\underline{\boxed{\sf{2(x - 11)(x + 11)}}}\)

Step-by-step explanation:

\(\sf{2x^2 - 242}\)

Common factor :

\(\sf{2x^2 - 242}\)

\(\sf{2(x^2 - 121)}\)

\( \: \: \: \: \: \: \: \: \: \: \: \: \)

Use the sum-product pattern :

\(\sf{2(x^2-121)}\)

\(\sf{2(x^2 + 11x-11x - 121)}\)

\(\: \: \: \: \: \: \: \: \: \: \: \: \)

Common factor from the two pairs :

\(\sf{2(x^2 + 11x-11x - 121)}\)

\(\sf{2(x(x+11) -11(x + 11))}\)

\(\: \: \: \: \: \: \: \: \: \: \: \: \)

Rewrite in factored form :

\(\sf{2(x(x+11)- 11(x + 11))}\)

\(\sf{2(x - 11)(x + 11)}\)

\(\: \: \: \: \: \: \: \: \: \: \: \: \)

Solution :

\(\sf{2(x - 11)(x + 11)}\)

Trevor and Kim will be situated 21 kilometers apart from each other at 1:30 PM. They will be separated by a distance of 21 km when the clock strikes 1:30 in the afternoon.

To determine at what time Trevor and Kim will be 21 km apart, we can set up a distance-time equation based on their relative speeds and distances.

Let's assume that t represents the time elapsed in hours since noon. At time t, Trevor would have traveled a distance of 8t km, while Kim would have traveled a distance of 6t km in the opposite direction.

Since they are running in opposite directions, the total distance between them is the sum of the distances they have traveled:

Total distance = 8t + 6t

We want to find the time when this total distance equals 21 km:

8t + 6t = 21

Combining like terms, we have:

14t = 21

To solve for t, we divide both sides of the equation by 14:

t = 21 / 14

Simplifying, we find:

t = 3 / 2

So, they will be 21 km apart after 3/2 hours, which is equivalent to 1 hour and 30 minutes.

Therefore, Trevor and Kim will be 21 km apart at 1:30 PM.

For more such question on distance . visit :

https://brainly.com/question/30395212

#SPJ8

A) Function is increasing on (-∞, -1) and (7/2, ∞), and decreasing on (-1, 7/2).

b)  The local minimum value of f is; 5608/2197 at x = -42/13, and the local maximum value of f is 139/8 at x = 7/2.

(a) To determine the intervals on which f is increasing or decreasing, we need to determine the critical points and then check the sign of the derivative on the intervals between them.

f(x)=8x³-42x-48x + 4

f'(x) = 24x² - 90

Setting f'(x) = 0, we get

24x² - 90 = 0

24x² = 90

x =±  √3.75

So, the critical points are;

x = -1 and x = 7/2.

We can test the sign of f'(x) on the intervals as; (-∞, -1), (-1, 7/2), and (7/2, ∞).

f'(-2) = 72 > 0, so f is increasing on (-∞, -1).

f'(-1/2) = -25 < 0, so f is decreasing on (-1, 7/2).

f'(4) = 72 > 0, so f is increasing on (7/2, ∞).

Therefore, f is increasing on (-∞, -1) and (7/2, ∞), and decreasing on (-1, 7/2).

(b) To determine the local maximum and minimum values of f, we need to look at the critical points and the endpoints of the interval (-1, 7/2).

f(-1) = -49

f(7/2) = 139/8

f(-42/13) = 5608/2197

Learn more about maximum value  here:

brainly.com/question/23504923

#SPJ4

Hi, this question is actually really simple.

Let's consider that one house = 7 matchsticks. This is because, if we count the first two squares given in your question, it will count to 7.

Now we understood that one house has 7 matchsticks. So, if we want two houses, then consider two more square of matchsticks. So, 12. Likewise, for 3 houses , add 2 more squares, thus resulting in 17. For four houses, again add 2 more squares, giving the result as 22 matchsticks.

Note- While adding two more squares for each, do not count the left side 2 matchsticks, as they are combined with the previous matchsticks. I meant that , if you want to know 2nd house matchsticks, count 7+7=14, then subtract 14-2, so 12

Now, the brief answer is:-

1 house = 7 matchsticks

2 houses = 12 matchsticks

3 houses = 17 matchsticks

4 houses = 22 matchsticks

5 houses = 27 matchsticks

Hope it helps you...

(Answered by Benjemin)

Answer:

2=14

3=21

4=28

5=35

Step-by-step explanation:

If 1 house =7 matchsticks

Then 2 houses = x

x=2×7=14 matchsticks

If 2 houses=14 matchsticks

3 houses=x

2x=14×3

Dividing both sides by 2

x=7×3=21

4=28

5=35

Hope it helps