a printer can print 27 pages in 4.5 minutes. how much time does it take to print 324 pages
Answers
Answer:
54
Step-by-step explanation:
27pages=4.5minutes
\(1 = \frac{4.5}{27} \)
\(324 = \frac{4.5}{27} \times 324\)
\(324 = 4.5 \times 12\)
324pages=54minutes
Hence, the printer can print 324pages in 54 minutes
Related Questions
evaluate the expression for the given variable
-4p+1 when p=2
Answers
(c) find the particular solution y f x to the given differential equation with the initial condition f 1 3 .
Answers
The particular solution of y = f(x) to the given differential equation \(\frac{dy}{dx} = y (xlnx)\) with the initial condition f(1) = 4 is \(y = 4e^{\frac{1}{2}x^{2} lnx } - \frac{1}{4} x^{2} + \frac{1}{4}\).
dy/dx = y(x lnx)
1/y dy = x lnx dx Eqn (1)
Let u = lnx, dv = x dx
Differentiate u = lnx
du = 1/x dx
Integrate dv = x dx
v = (1/x)x²
Now, integrate equation(1), we get
∫1/y dy = ∫x lnx dx
ln y = 1/2 x² ln x - 1/4 x² + C Eqn (2)
Now, put the value of x and y to calculate the value of C
ln 4 = 1/2 ln 1 - 1/4 + C
ln 4 + 1/4 = C
Put the value of C in equation (2), and we get
ln y = 1/2 x² ln x - 1/4 x² + ln 4 + 1/4
\(y = 4e^{\frac{1}{2}x^{2} lnx } - \frac{1}{4} x^{2} + \frac{1}{4}\)
--The given question is incorrect, the correct question is
''Find the particular solution y = f (x) to the given differential equation \(\frac{dy}{dx} = y (xlnx)\) with the initial condition f(1) = 4."--
To know more about differential equation, here
https://brainly.com/question/14598404
#SPJ4
A tapered cylinder is made by decreasing the radius of a rod continuously as you move from one end to the other. The rate at which it tapers is the taper per foot. You can calculate the taper per foot using the formula T= 24(R-r)/L. The lengths R, r , and L are measured in inches.
b. What is L for T=0.75,0.85 , and 0.95 , if R=4 in.; r=3 in.?
Answers
For a tapered cylinder with a taper per foot (T) of 0.75, 0.85, and 0.95, and given that the initial radius (R) is 4 in.
To find the length (L) for each taper per foot (T), we can rearrange the formula T= 24(R-r)/L to solve for L. Substituting the given values of R=4 in. and r=3 in., we have:
0.75 = 24(4-3)/L
0.85 = 24(4-3)/L
0.95 = 24(4-3)/L
Simplifying these equations, we get:
0.75L = 24
0.85L = 24
0.95L = 24
Dividing both sides of each equation by the corresponding coefficient, we find:
L = 24/0.75
L = 24/0.85
L = 24/0.95
Evaluating these expressions, we get:
L ≈ 32 in.
L ≈ 28.24 in.
L ≈ 25.26 in.
Therefore, the length (L) for taper per foot values of 0.75, 0.85, and 0.95, with R=4 in. and r=3 in., are approximately 32 in., 28.24 in., and 25.26 in., respectively.
Learn more about equation: brainly.com/question/29174899
#SPJ11
if cos A=12\13 then find sin Aand tan A[A<90°
Answers
Step-by-step explanation:
sinA = perp/base
sinA = 5/12
TanA = perp/base = 5/12
46.6 rounded to the nearest hundredth
Answers
The hundredth is the second place after the decimal. So the 6 to the right after the decimal is the tenth place, the number after that would be the hundredth place. But there is no hundredth place.
5 and 9 are the example of ____ number
Answers
Answer:
Step-by-step explanation:
complex numbers , real numbers , rational numbers , natural numbers , whole numbers
Is this correct?
8EF625DF

Answers
The missing angles of the given complementary and supplementary angles above would be listed below as follows:
Angle1= 12°
Angle2= 145°
Angle3= 15°
Angle 4= 77°
Angle 5= 110°
What are complementary and supplementary angles?A complementary angle is the type of angle that is made up of two angles that adds up to 90°, while a supplementary angle is the type of angle that that is made up of two angles that adds up to 180°.
For Angle1:
X = 90-78 = 12°
Angle2:
X = 180-35 = 145°
Angle3:
X = 90-75 = 15°
Angle 4:
X = 90-13 = 77°
Angle 5:
X = 180-70 = 110°
Learn more about complementary angles here:
https://brainly.com/question/27576425
#SPJ1
angles not necessarily drawn to scale ×=______

Answers
Answer:
Step-by-step explanation:
these are vertical opposing angles
x=20+25=45 degrees
Help! “Ms.Day drew a rectangle on the board with a width of 14 cm and a digo al length of 50 cm. Find the length of this rectangle in centimeters.”

Answers
Answer:
length=48cm
Step-by-step explanation:
a²+14²=50²
a²+196=2500
a²=2304
a=48
(-3/7 -2p)2
whoever solves this has big brain lol
Answers
1. Apply the Commutative Property to the problem below to create a new problem.
Problem: 5g + 9
2. Apply the Associative Property to the problem below to create a new problem.
Problem: 57•9•c
Answers
57.9.c can be written as 57c . 9
Suppose an and bn are series with positive terms and bn is known to be convergent. (a) If an > bn for all n, what can you say about an? Why? O a n converges if and only if an < 2bn. Oman converges by the Comparison Test. O an diverges by the Comparison Test. We cannot say anything about an. o a n converges if and only if an 5 4bn. (b) If an
Answers
Nothing that we can say regarding an we are unsure of whether the terms of an are rising or falling, a passes the Comparison Test and sequence, Since bn, an also converges.
what is a sequence?A collection of numbers, or "terms," is referred to as a sequence. Examples of terms are 2, 5, and 8. Some sequences can be made endlessly lengthy by taking advantage of a particular pattern they follow. Use the example of 2,5,8 and add 3 to continue the sequence.
We are unable to comment on an.
This is due to the fact that bn converges, causing a to exceed bn, and as a result, we are unable to determine whether the terms of an are increasing or decreasing.
What can you say about an if a bn for all n? a passes the Comparison Test and converges.
This is due to the fact that since bn converges and a converges since bn, we may infer that the terms of an are likewise decreasing and that an also sequence since bn based on the comparison test.
To know more about sequence visit:
https://brainly.com/question/21961097
#SPJ4
please help me answer this

Answers
Answer:
pie
Step-by-step explanation:
HELP PLEASE!! SOLVE FOR "X"

Answers
Answer:
\(x=\frac{c^2y^2}{4}\)
Step-by-step explanation:
\(\frac{2\sqrt{x}}{c}=y\\\\2\sqrt{x}=cy\\\\\sqrt{x}=\frac{cy}{2}\\\\x=\frac{c^2y^2}{2^2}\\\\x=\frac{cy}{4}\)
Answer:
c²y²
x = ----------
4
Step-by-step explanation:
Let's isolate √x: Multiply both sides of this equation by c/2. We get:
c*y
√x = ---------
2
To find an expression for x, square both sides of this result:
cy
x = {------ }²
2
This is equivalent to:
c²y²
x = ----------
4
The Naturally Made Bath and Body store pays $550 a month for rent and utilities. The average cost for its products to be manufactured is about $3.00 an item. If the average price for a product sold in the store is $5.50, what will the break-even point be?
Answers
Answer:
Break-even point is at quantity 220.
Step-by-step explanation:
Given the rent amount that is fixed cost for the store = $550
The average cost of the goods = $3
The average price of the goods = $5.50
Let the total number of break-even items = Q
Thus, total revenue = 5.50 x Q = 5.50Q
At break-even, TR = TC
5.50Q = FC + VC
5.50Q = 550 + 3Q
5.50Q - 3Q = 550
2.50Q = 550
Q = 550 / 2.50
Q = 220
Thus break-even point is at quantity 220.
if the radius of a cone is doubled and the height remains the same, what effect does this have on the volume of the original cone?
Answers
If the radius of a cone is doubled and the height remains the same, the volume of the original cone will be affected. To understand this effect, we must first understand the formula for calculating the volume of a cone. The formula is V = (1/3)πr^2h, where V is the volume, r is the radius, and h is the height.
When the radius of a cone is doubled, we can see that this change will affect the value of r in the formula. If we substitute 2r for r in the formula, we get V = (1/3)π(2r)^2h. Simplifying this equation gives us V = (4/3)πr^2h. This tells us that the volume of the original cone will be multiplied by a factor of four when the radius is doubled and the height remains the same.
In summary, if the radius of a cone is doubled and the height remains the same, the volume of the original cone will be multiplied by a factor of four. This is because the formula for calculating the volume of a cone involves the radius raised to the second power, which means that doubling the radius will quadruple the volume of the cone.
To know more about radius of a cone visit :-
https://brainly.com/question/29772997
#SPJ11
In the game of roulette, a steel ball is rolled onto a wheel that contains 18 red, 18 black, and 2 green slots. If the ball is rolled 25 times, find the probabilities of the following events. The ball falls into the green slots two or more times. The ball does not fall into the green slots. The ball falls into black slots 15 or more times. The ball falls into red slots 10 or fewer times.
Answers
The required probabilities for the events in question are:
0.000800.9992\(2.21\times10^{-8}\)\(1.63\times10^{-8}\)Based on the parameters given :
Number of red slots = 18
Number of black slots = 18
Number of green slots = 2
Total number of slots = 18+18+2 = 38
A.)
Probability of green slots 2 or more times :
(2/38)² × (36/38)²³ = 0.00080
B.)
Probability of ball not entering the green slots
1 - P(green slots)
P(not entering green slot ) = 1 - 0.0008 = 0.9992
C.)
probability that ball falls into black slot 15 or more times :
(18/38)¹⁵ * (20/38)¹⁰ = \(2.21\times10^{-8}\)
D.)
Probability that ball falls into red slot 10 or less times :
(10/38)¹⁰ * (28/38)¹⁵ = \(1.63\times10^{-8}\)
Therefore, the required probabilities are :
0.000800.9992\(2.21\times10^{-8}\)\(1.63\times10^{-8}\)Learn more on probability:https://brainly.com/question/15246027
#SPJ4
During a thunder storm, the amount of rain on the ground increased at an average rate of 0.25 inch per hour. There was already 4.5 inches of rain on the ground when the storm started. Write an equation that can be used to determine the total amount of rain on the ground (T), in inches, after h hours of the storm.
Answers
Explanation: 4.5 inches of rain already exist on the ground and 0.25 inches are being added every hour. And since the amount of hours are “T”, the amount of rain after T hours will be 0.25T
how many planes contain the same three collinear points?
Answers
Answer:
The points are collinear if the slope of any two pair of points is the same. Many infinite planes pass through that line. Thus, there are infinite planes contain the same three collinear plane.
Answer:
infinitely many
Step-by-step explanation:
well if you think about it in a 3D plane
we can make to planes intercept at a line
and we can make another plane that another plane interceptes the other to planes in the same line
and another
and another
...
so we can have three points in the line (collinear) that the planes intercept and we are done
What is = s
What is x=

Answers
Considering the similar triangles, the measures of the angles are given as follows:
s = w.x = y.What are similar triangles?Similar triangles share these two features:
Congruent angles, that is, angles that have the same measure.Proportional side lengths.For this problem, the triangles are similar, with the arrow representing the corresponding sides, moving from angle w to angle x in one triangle, and from angle y to angle s in the other triangle.
Hence the measures of the angles are given as follows:
s = w.x = y.More can be learned about similar triangles at brainly.com/question/11920446
#SPJ1
Solve for the value of x

Answers
Answer:
x = 50°
Step-by-step explanation:
130 and x are adjacent angles on a straight line and sum to 180° , so
x + 130° = 180° ( subtract 130° from both sides )
x = 50°
X = 50
Why? Because x + 130 is on a straight line. And the angle of a straight line is 180.Therefore , take 130 subtracted by 180 to get ur ans!!
Hope this helps!! ^^
What is the value of (2/5)^3
Answers
The value of the exponent (2/5)^3 is \(\frac{8}{125}\)
In the above question, it is given that
(2/5)^3
The number of times a number has been multiplied by itself is referred to as an exponent. For instance, the expression 2 to the third (written as 2^3) signifies 2 x 2 x 2 = 8.
We need to solve it and then find the value of the exponent
(2/5)^3
= \(\frac{2}{5}\) x \(\frac{2}{5}\) x \(\frac{2}{5}\)
= \(\frac{2 . 2. 2}{5 . 5 . 5}\)
= \(\frac{8}{125}\)
Therefore the value of the exponent (2/5)^3 is \(\frac{8}{125}\)
To learn more about, exponential here
https://brainly.com/question/219134
#SPJ1
simplify
(8p^6)^1/3
simplifyyyyyyyyyyyyyyyyyyyyyyyyyyyyyy
Answers
Answer:
\(2p^2\)
Step-by-step explanation:
Step 1: Apply the exponentiation property:
\((8p^6)^\frac{1}{3} = 8^\frac{1}{3} * (p^6)^\frac{1}{3}\)
Step 2: Simplify the cube root of 8:
The cube root of 8 is 2:
\(8^\frac{1}{3} =2\)
Step 3: Simplify the cube root of \((p^6)\):
The cube root of \((p^6)\) is \(p^\frac{6}{3} =p^2\)
Step 4: Combine the simplified terms:
\(2 * p^2\)
So, the simplified expression is \(2p^2\).
The garden itself is 5 yards by 8 yards. The total area need to build this landscape
design is 60.9525 square yards. What is the width of the walkway?
O a) 0.725 yards
b) 2.9 yards
C) 1.45 yards
d) 4.58 yards
Answers
Answer: 1.45
Step-by-step explanation:
Find the missing side. Round your answer to the nearest tenth. 19, 36
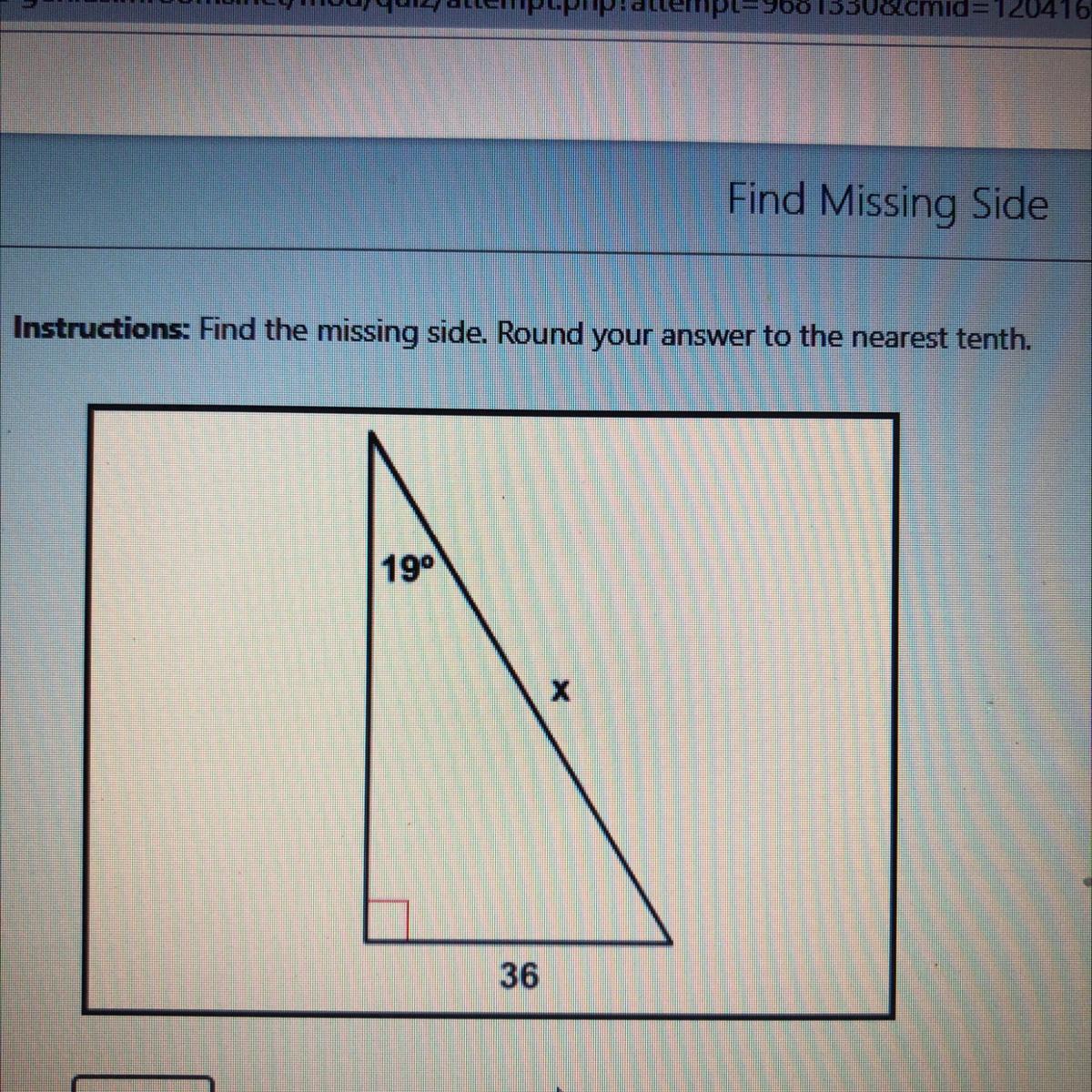
Answers
Answer:
x=110.6
Step-by-step explanation:
sin(19)=36/x. x=36/sin(19)=110.6
Amanda was given the following polynomial and asked to factor completely. Find the errors that she made and explain how to fix her errors.

Answers
Answer:
The error in Amanda's calculation is in line 2, where she incorrectly subtracted 6x instead of adding 6x, as well as incorrectly subtracting 24 instead of adding 24. Amanda also omitted the addition sign in line 3 of her calculations.
Step-by-step explanation:
To factor a quadratic polynomial in the form ax² + bx + c, find two numbers that multiply to ac and sum to b.
Therefore, for the given polynomial 4x² + 22x + 24:
⇒ ac = 4 · 24 = 96
⇒ b = 22
The factors of 96 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, and 96.
Therefore, the factor pair that sums to 22 is 16 and 6.
Rewrite b as the sum of these two numbers:
⇒ 4x² + 22x + 24
⇒ 4x² + (16 + 6)x + 24
⇒ 4x² + 16x + 6x + 24
Therefore, the error in Amanda's calculation is in line 2, where she incorrectly subtracted 6x instead of adding 6x, as well as incorrectly subtracting 24 instead of adding 24. Amanda also omitted the addition sign in line 3 of her calculations.
The correct calculation is as follows:
4x² + 22x + 24
⇒ 4x² + 16x + 6x + 24
⇒ 4x(x + 4) + 6(x + 4)
⇒ (4x + 6)(x + 4)

Given :-
A polynomial 4x² + 22x + 24 .To find:-
The mistakes made by Amanda and how to fix the mistakes.Answer:-
Given polynomial to us is ,
\(\implies 4x^2 + 22x + 24 \\\)
With respect to the standard form of polynomial ax² + bx + c , we have;
a = 4 and c = 24Step 1 :- Split the middle term into two parts p and q such that p × q = a × c and p + q = b
Such two numbers are 16 and 6 .
Hence, we can rewrite it as ,
\(\implies 4x^2 + 16x + 6x + 24 \\\)
But Amanda wrote \( 4x^2+16x - 6x + 24\) , so she made a mistake here by writing +6x as -6x .
Step 2:- Factor out the common terms .
\(\implies 4x( x + 4) + 6(x+4) \\\)
Step 3 :- Take out \( x+4\) as common.
\(\implies (x+4)(4x+6) \\\)
This is our required factored form .
Hence we can see that Amanda made a mistake only in splitting the term term .
and we are done!
What is the value of x in the equation 8x - 2y = 48, when y = 4?
O 6
07
O 14
O 48
Answers
Answer:
The answer is option 2.
Step-by-step explanation:
You have to substitute the value of y into the equation :
\(8x - 2y = 48\)
\(let \: y = 4\)
\(8x - 2(4) = 48\)
\(8x - 8 = 48\)
\(8x = 48 + 8\)
\(8x = 56\)
\(x = 56 \div 8\)
\(x = 7\)
The value of x in the equation 8x - 2y = 48 is 7.
What is Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
We have,
8x - 2y = 48
Now, for y=4 put the value of y as 4 in given equation we get
8x- 2(4)= 48
8x -8= 48
8x = 48+ 8
8x = 56
x= 56/8
x= 7
Thus, the value of x is 7.
Learn more about Equation here:https://brainly.com/question/29657983
#SPJ2
In the figure below, parallel lines AB and CD are cut by transversals AC and BD They intersect at E. Two angle measures are given. What is the measure of angle ABD?
20 points to help me

Answers
Answer:
Step-by-step explanation:
????????
Answer:
A : 146
Step-by-step explanation:
Since the lines AB and CD are parallel, we know that the angle opposite to BDC is also 34. To find ABD we can do 180-34 , which gives us 146
Im so lost please help! Circle Y has points W, T,V, and U on the circle. Secant lines WM and UM intersect at point M outside the circle. The mUW = 145°, mTV = 31°, and m


Answers
A formula that can be used to find the value of x MU² - UM * MV - MV * TV = x² * (MU - UM). The value of x is x ≈ ±3.55.
What is angle measures?Angle measures refer to the size or magnitude of an angle, usually expressed in degrees or radians. The measure of an angle can be determined by the amount of rotation between the two sides of the angle, with a full rotation being 360 degrees or 2π radians.
According to question:1) From the given information, we know that <UMV is an exterior angle of triangle TMV, so <UMV = <TMV + <MTV. Substituting the given angle measures, we get:
m<UMV = x² + 31
Also, by the intersecting secants theorem, we have:
MU * MW = MV * MT
Substituting the given segment lengths, we get:
(MU + UW) * (MU - UW) = MV * TV
Simplifying this equation, we get:
MU² - UW² = MV * TV - UW * MU
Substituting the given angle measure and simplifying further, we get:
MU² - UW² = MV * TV - UW * MU
MU² - MW² - UW² = -UW * MU
(MU - MW) * (MU + MW) - UW² = -UW * MU
(MU + MW) = (UW² - MU * UW) / (MU - UW)
Substituting the given angle measure, we get:
tan(145) = UW / UM
Simplifying this equation, we get:
UW = UM * tan(145)
Substituting this expression for UW, we get:
MU + UM * tan(145) = (UM² - MU * UM) / (MU - UM)
Simplifying further, we get:
MU² - UM * MV - MV * TV = x² * (MU - UM)
2) Substituting the given angle measures and segment lengths into the formula from part 1, we get:
MU² - UM * MV - MV * TV = x² * (MU - UM)
MU² - 2 * MU * MV * sin(31) - MV * sin(x²) = x² * (MU - UM)
Substituting the expression for UW from part 1, we get:
MU + UM * tan(145) = (UM² - MU * UM) / (MU - UM)
MU² - MU * UM - UM * tan(145) = -MU * (MU - UM)
MU * (MU - UM + UM * tan(145)) = MU² - UM * tan(145)
MU = (UM * tan(145)) / (1 - tan(145))
Substituting this expression for MU, we get:
(UM * tan(145))² / (1 - tan(145)) + UM * MV * sin(31) - MV * sin(x²) = x² * ((UM * tan(145)) / (1 - tan(145)) - UM)
Simplifying this equation and solving for x, we get:
x ≈ ±3.55
To know more about angle measures visit:
https://brainly.com/question/30958464
#SPJ1
A formula that can be used to find the value of x MU² - UM * MV - MV * TV = x² * (MU - UM). The value of x is x ≈ ±3.55.
What is angle measures?Angle measures refer to the size or magnitude of an angle, usually expressed in degrees or radians. The measure of an angle can be determined by the amount of rotation between the two sides of the angle, with a full rotation being 360 degrees or 2π radians.
According to question:1) From the given information, we know that <UMV is an exterior angle of triangle TMV, so <UMV = <TMV + <MTV. Substituting the given angle measures, we get:
m<UMV = x² + 31
Also, by the intersecting secants theorem, we have:
MU * MW = MV * MT
Substituting the given segment lengths, we get:
(MU + UW) * (MU - UW) = MV * TV
Simplifying this equation, we get:
MU² - UW² = MV * TV - UW * MU
Substituting the given angle measure and simplifying further, we get:
MU² - UW² = MV * TV - UW * MU
MU² - MW² - UW² = -UW * MU
(MU - MW) * (MU + MW) - UW² = -UW * MU
(MU + MW) = (UW² - MU * UW) / (MU - UW)
Substituting the given angle measure, we get:
tan(145) = UW / UM
Simplifying this equation, we get:
UW = UM * tan(145)
Substituting this expression for UW, we get:
MU + UM * tan(145) = (UM² - MU * UM) / (MU - UM)
Simplifying further, we get:
MU² - UM * MV - MV * TV = x² * (MU - UM)
2) Substituting the given angle measures and segment lengths into the formula from part 1, we get:
MU² - UM * MV - MV * TV = x² * (MU - UM)
MU² - 2 * MU * MV * sin(31) - MV * sin(x²) = x² * (MU - UM)
Substituting the expression for UW from part 1, we get:
MU + UM * tan(145) = (UM² - MU * UM) / (MU - UM)
MU² - MU * UM - UM * tan(145) = -MU * (MU - UM)
MU * (MU - UM + UM * tan(145)) = MU² - UM * tan(145)
MU = (UM * tan(145)) / (1 - tan(145))
Substituting this expression for MU, we get:
(UM * tan(145))² / (1 - tan(145)) + UM * MV * sin(31) - MV * sin(x²) = x² * ((UM * tan(145)) / (1 - tan(145)) - UM)
Simplifying this equation and solving for x, we get:
x ≈ ±3.55
To know more about angle measures visit:
https://brainly.com/question/30958464
#SPJ1
calculate length of AB
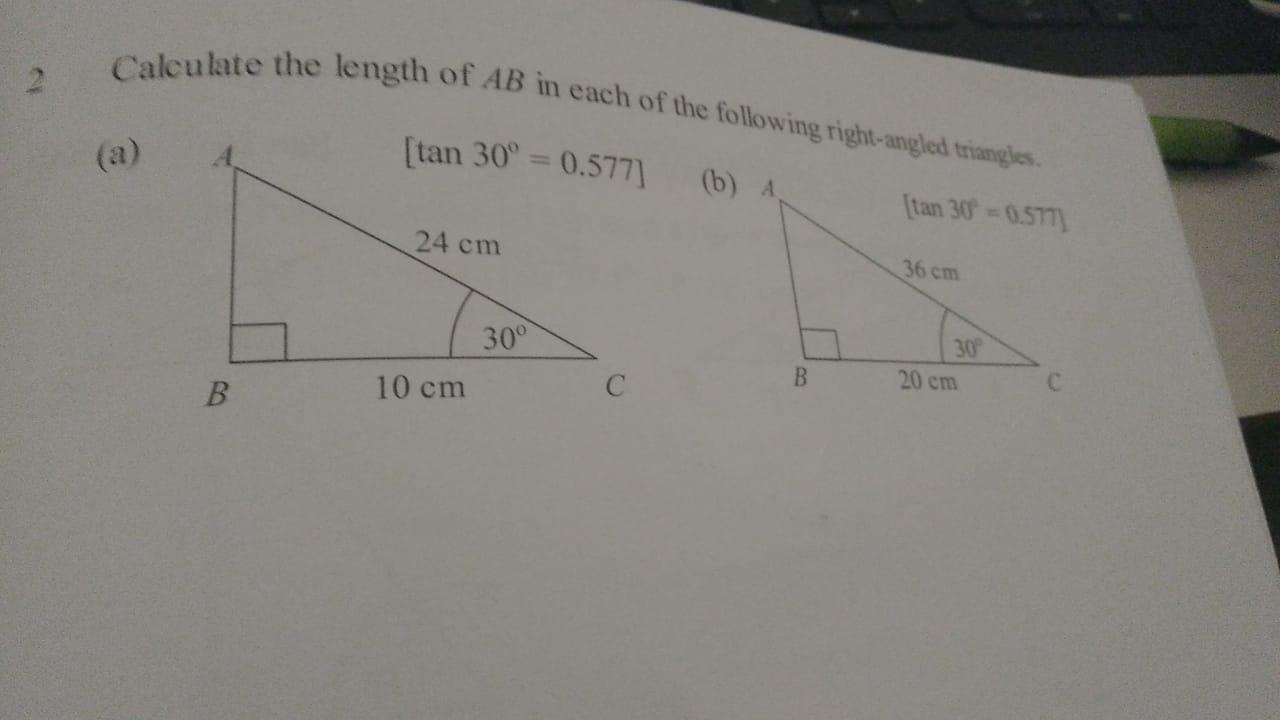
Answers
Answer:
a) 21.817
b) 29.93
Step-by-step explanation:
a)
solution:
By using Pythagoras theorem
AB = √(AC²-BC²)
= √(24²-10²)
= √476
= 21.817
b)
solution:
By using Pythagoras theorem
AB=√(AC²-BC²)
=√(36²-20²)
=√896
=29.93