A plot of land is valued at $18,000.Land tax is charged at the rate of 0.70 per $100. What is the total amount of tax paid for the land?
Answers
Answer:
The total amount of tax paid for the land was $126
Step-by-step explanation:
Proportions
The land tax charged is 0.7 per each $100 of the land value. For easy calculations, we find the ratio or proportion to be applied to the value of the land as:
0.7 / 100 =0.007
This factor can be used to obtain the tax charged for a given value of the land.
The plot of land of the question is valued at $18,000.
The tax charged is, then:
0.007*18,000 = 126
The total amount of tax paid for the land was $126
Related Questions
easy one - giving brainly - show work.
75% of what number is 48?
Answers
Step-by-step explanation:
the required number is 64 .
which of the following is a polynomial function
Answers
Answer:
I think questions is not complete.
**Answers needed fast please**

Answers
Its answers hope it’s help
2т - 7 = 5х +8
Can u help me plzzzzz
Answers
Answer:
The answer is X=5
Step-by-step explanation:
2x - 5x = 7-8
-3x = -15
X= -15: (-3)
X=5
Fatima conducts emissions inspections on cars. She finds that 6\%6%6, percent of the cars fail the inspection. Let ccc be the number of cars fatima inspects until a car fails an inspection. Assume that the results of each inspection are independent.
Answers
The probability that the first failed inspection occurs on Fatima's 5th inspection i.e P(c = 5) is 0.05..
Geometric probability distribution:In probability and statistics,the geometric distribution defines the probability of the first success occurring after k trials. The probability of success is p
P r ( X = k ) = ( 1 − p )⁽ᵏ⁻¹⁾ p.
We have given that,
An emissions inspections on cars is conducted by Fatima.
Probability that car fail the inspection, p = 6% = 0.06
let c denoted the number of cars that are inspected until one car fail to inspection.
The random variable c here. Here c follow geometric probability distribution with probability of success (0.06).
Plugging all known values in above formula we get, p(c= 5) = (1-0.06)⁴ × 0.06
= (0.94)⁴ (0.06)
=0.0468449376~ 0.05
so, the answer is 0.05
To learn more about Geometric probability distribution, refer:
https://brainly.com/question/18096310#SPJ4
Complete question:
Fatima conducts emissions inspections on cars. She finds that 6%, percent of the cars fail the inspection. Let C be the number of cars Fatima inspects until a car fails an inspection. Assume that the results of each inspection are independent.
Required:
Find the probability that the first failed inspection occurs on Fatima's 5th inspection
THIS IS MY 20TH TIME POSTING THIS PLS HELP QUICK PLSSS :’( Which of the following equations describes the line shown below? Check all that apply. (-5,6) (-1,-1)

Answers
Answer:
i think b and e
Step-by-step explanation:
I give 20 points!!!
If I get 50 euros per month, how many months I need to buy a product for 640 euros
Answers
50+50+50+50+50+50+50+50+ 50+50+50+50+50= 650 which is enough to buy the product
Suppose that R(x) is a polynomial of degree 13 whose coefficients are real numbers. also, suppose that R(x) has the following zeros. answer the following.edit: if possible please double check the answers just to be safe.

Answers
(a) Complex zeros of a polynomial come in pairs.
If a + bi is a zero of a polynomial then its conjugate a - bi is also a zero of the polynomial.
The given complex zeros of R(x) are 1 + 3i and -2i.
1 - 3i is the conjugate of 1 + 3i.
Hence, another zero of R(x) is 1 - 3i
b)
Since the polynomial R(x) is of order 13 then R(x) must have 13 zeros.
The given complex zeros of R(x) are 1 + 3i and -2i. We also know that the conjugates of 1 + 3i and -2i are zeros of R(x). Hence, R(x) has at least 4 complex roots
Hence, the maximum number of real zeros of R(x) is (13 -4).
The maximum number of real zeros of R(x) is 9
c) Let the maximum number of nonreal zeros (complex roots) be n
Complex roots come in pairs. Therefore, n must be even.
Hence, n ≤ 13 - 1 = 12
n ≤ 10
We have been given a real zero of R(x), 3 ( With the multiplicity of 4).
12 - 4 = 8
Therefore,
n ≤ 8.
Hence the maximum number of nonreal zeros of R(x) is 8
Sophia is going to invest $820 and leave it in an account for 12 years. Assuming the interest is compounded monthly, what interest rate, to the nearest tenth of a percent, would be required in order for Sophia to end up with $1,170?
Answers
Answer:2.90%
Step-by-step explanation: good luck!
Solve this equation: 6y = -42
Answers
\(\text {Hi! Let's Solve this Equation!}\)
\(\text {The Only Step you need to do is Divide 6:}\)
\(\text {6y/6=-42/6}\)
\(\text {Your Answer would be:}\)
\(\fbox {y=-7}\)
\(\text {Best of Luck!}\)
\(\text {-LimitedX}\)
Answer:
-7
Step-by-step explanation:
6y =-42
y=-42:6
y=-7
find the midpoint and distance between (5,1) and (-15,11)
Answers
Answer:
look i think is -5.005 I don't really know but I hope you get it right. Have a good day
Government data show that 26% of the civilian labor force has at least 4 years of college and that 15% of the labor force works as laborers or operators of machines or vehicles. Can you conclude that because (0.26)(0.15) = .039 about 4% of the labor force are college-educated laborers or operators?
(a) Yes, by the multiplication rule
(b) Yes, by conditional probabilities
(c) Yes,bythelawoflargenumbers
(d) No, because the events are not independent
(e) No, because the events are not mutually exclusive
d
Answers
Option (d)- No, because the events are not independent. Hence we can not conclude that because (0.26)(0.15) = 0.039 about 4% of the labor force are college-educated labors or operators.
We have given that government data show that 26% of the civilian labor force has at least 4 years of college and that 15% of the labor force works as laborers or operators of machine or vehicle.
So here,
event A = 26% of civilian labor force hast at least 4 years of college
event B = 15% of the labor force works as laborers or operators of machines or vehicles
Therefore it is observe that both the events are not independent.
Hence we cannot conclude that because (0.26)(0.15) = 0.039 about 4% of the labor force are college-educated laborers or operators.
To know more about labors here
https://brainly.com/question/17136480
#SPJ4
Please help Factor the expression using the GCF the expression 32z-48 factored using the GCF is
Answers
Answer:
16(2z -3)
Step-by-step explanation:
There are two ways of solving this problem.
List out the factors of the numbers:
32z - 48
= 32 * z - 48
32= 1, 2, 4, 8, 16, 32
48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
the largest common factor that both numbers have in common is 16,
So factoring the equations means the one has to divide the equation by 16 and write it outside of the parenthesis.
16 * ( 2 * z - 3)
16(2z -3)
Another way of solving the problem:
prime factorize the number:
32 = 2^5
48 = 2^4 * 3
Both numbers have 2^4 as their largest factor in common meaning that that is their GCF. 2^4 is 16.
Now factor out 16 and write it on the outside of the parenthesis.
16 * ( 2 * z - 3)
16(2z -3)
Answer:
16(2z -3)
Step-by-step explanation:
I need help with the question ASAP

Answers
Answer:
3. d
4.b
5.a
6. is 15
Step-by-step explanation:
mn=5
no=5
op=10
pq=10
Which expression is equivalent to 5m - (2m - 8) + 12 + 6m?
Answers
\(=5m-2m+8+12+6m\\=5m-2m+6m+8+12\\=3m+6m+20\\=9m+20\)
The answer is 9m+20,it is equivalent to the expression in the question.
A rental car company charges $22. 50 per day to rent a car and $0. 10 for every mile driven. Salma wants to rent a car, knowing that: she plans to drive 275 miles. She has at most $140 to spend. Write and solve an inequality which can be used to determine dd, the number of days salma can afford to rent while staying within her budget.
Answers
Salma can therefore rent the vehicle for a maximum of 5 days and go 275 miles. When A rental car company charges $22. 50 per day to rent a car and $0. 10 for every mile driven. Salma wants to rent a car, knowing that: she plans to drive 275 miles. She has at most $140 to spend.
Define inequality.In mathematics, inequalities specify the connection between two non-equal numbers. Equal does not imply inequality. Typically, we use the "not equal sign (≠)" to indicate that two values are not equal. But several inequalities are utilized to compare the numbers, whether it is less than or higher than.
Given
Although your question is incomplete, you might be referring to the following in its entirety: Renting a car from a rental car agency costs $22.50 per day plus $0.10 every mile driven. Salma wants to rent a car because she knows she will go 275 kilometres. She can only spend up to $140. The number of days Salma can rent the car for while staying within her budget can be calculated by writing and solving an inequality.
The formula that solves this issue is:
Let x represent how many days Salma can afford to rent the automobile for.
Inequality
22.5x + 0.10(275) ≤ 140
22.5x + 2.75 ≤ 140
22.5x ≤ 140 - 2.75
22.5x ≤ 137.25
x ≤ 5
automobile rental on a daily basis get x <= 5
Salma can therefore rent the vehicle for a maximum of 5 days and go 275 miles.
To learn more about inequality, visit:
https://brainly.com/question/28662304
#SPJ4
HELPZ. Find value of x and all the measures of all angel

Answers
Answer: x = 40
have: ∠A + ∠B + ∠C + ∠D = 180°
⇔ x + 6 + x + 4 + x +10 + x = 180°
⇔ 4x + 20 = 180
⇔ x = (180 - 20)/4
⇔ x = 160/4 = 40
Step-by-step explanation:
Calculate ∬sf(x,y,z)ds for x2 y2=9,0≤z≤1;f(x,y,z)=e−z ∬sf(x,y,z)ds=
Answers
The surface integral ∬s f(x,y,z) ds for x² + y² = 9, 0 ≤ z ≤ 1, and f(x,y,z) = \(e^{-z\) is -3(e⁻¹ - 1).
To calculate the surface integral ∬s f(x,y,z) ds for x^2 + y^2 = 9 and 0 ≤ z ≤ 1, where f(x,y,z) = e^(-z), we can use the parametric form of the surface S as:
x = 3 cosθ
y = 3 sinθ
z = z
where θ varies from 0 to 2π, and z varies from 0 to 1.
Next, we need to find the partial derivatives of the parametric form of the surface S with respect to the parameters θ and z:
∂r/∂θ = [-3 sinθ, 3 cosθ, 0]
∂r/∂z = [0, 0, 1]
Then, we can find the surface area element ds using the formula:
ds = ||∂r/∂θ x ∂r/∂z|| dθ dz
where ||∂r/∂θ x ∂r/∂z|| is the magnitude of the cross product of ∂r/∂θ and ∂r/∂z.
Evaluating this expression, we get:
||∂r/∂θ x ∂r/∂z|| = ||[3 cosθ, 3 sinθ, 0]|| = 3
So, the surface area element becomes:
ds = 3 dθ dz
Finally, we can write the surface integral as a double integral over the region R in the θ-z plane:
∬s f(x,y,z) ds = ∬R f(r(θ,z)) ||∂r/∂θ x ∂r/∂z|| dθ dz
Substituting the parametric form of the surface S and the function f(x,y,z), we get:
∬s f(x,y,z) ds = ∫0¹ ∫\(0^{(2\pi)} e^{(-z)} 3\) dθ dz
Evaluating the inner integral with respect to θ, we get:
∬s f(x,y,z) ds = ∫0¹ 3 \(e^{(-z)\) dθ dz
Evaluating the outer integral with respect to z, we get:
∬s f(x,y,z) ds = [-3 \(e^{(-z)\)] from 0 to 1
∬s f(x,y,z) ds = -3(e⁻¹ - 1)
Therefore, the surface integral ∬s f(x,y,z) ds for x² + y² = 9, 0 ≤ z ≤ 1, and f(x,y,z) = \(e^{-z\) is -3(e⁻¹ - 1).
To know more about surface integral, refer to the link below:
https://brainly.com/question/32088117#
#SPJ11
We have to simplify by factorizing
How to solve it

Answers
—————
2x-3

ecovery
Translate the triangle.
Then enter the new coordinates.
(-1,2)
A'([?], [])
B'([ ], [])
C'([ ], []).
(-5,-1)
(В
(-2,-3)
< 4,6 >
Answers
Answer:
A'(3, 2 ), B'(6, 6 ),C'(6, - 3 )
A translation of 2 units right is equivalent to adding 2 to the x- coordinate with no change to the y- coordinate.
A(1, 2 ) → A'(1 + 2, 2 ) → A'(3, 2 )
B(4, 6 ) → B'( 4 + 2, 6 ) → B'(6, 6 )
C(4, - 3 ) → B'(4 + 2, - 3 ) → B'(6, - 3 )
Step-by-step explanation:
Hope this helps:)
At a certain factory, output is given by Q= 90K²/³L¹/3, where K is the capital
investment (in thousand of US$) and L is the size of the labor force, measured in
worker-hours. If output is kept constant, at what rate is capital investment changing at
a time when K = 27, L = 1,000, and L is increasing at the rate of 80 worker-hours per
week?
Answers
The rate at which capital investment (K) is changing while keeping output constant is -2,160 thousand US$ per unit of time.
We have,
The given output function is:
Q = (90K^2/3)(L^1/3)
To differentiate with respect to time (t), we use the chain rule and product rule of differentiation.
dQ/dt = (dQ/dK)(dK/dt) + (dQ/dL)(dL/dt)
Since the output is kept constant, dQ/dt is zero.
The rate of change of capital investment, dK/dt, is what we want to find.
We are given K = 27 and L = 1,000.
We also know that dL/dt = 80 worker hours per week.
Differentiating the output function with respect to K and L, we have:
(dQ/dK) = (2/3)(90K^(-1/3))(L^1/3)
(dQ/dL) = (1/3)(90K^2/3)(L^(-2/3))
Substituting the given values into the derivatives,
We have:
0 = (2/3)(90(27)^(-1/3))(1,000^1/3)(dK/dt) + (1/3)(90(27)^(2/3))(1,000^(-2/3))(80)
Simplifying the equation, we can solve for dK/dt:
0 = (2/3)(90(27)^(-1/3))(1,000^1/3)(dK/dt) + (1/3)(90(27)^(2/3))(1,000^(-2/3))(80)
Solving for dK/dt, we get:
dK/dt = -[(1/3)(90(27)^(2/3))(1,000^(-2/3))(80)] / [(2/3)(90(27)^(-1/3))(1,000^1/3)]
Simplifying further, we find:
dK/dt = -[(27)^(2/3)(1,000)^(-2/3)(80)] / [(27)^(-1/3)(1,000)^(1/3)]
dK/dt = -[(27)^(2/3)(80)] / [(27)^(-1/3)]
dK/dt = -[27^(2/3) x 80 x 27^(1/3)] / 27^(-1/3)
dK/dt = -27^(2/3 + 1/3) x 80 / 27^(-1/3)
dK/dt = -27 x 80 / 27^(-1/3)
dK/dt = -2,160
Therefore,
The rate at which capital investment (K) is changing while keeping output constant is -2,160 thousand US$ per unit of time.
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ1
1) What percentage of a dollar is the value of this coin combination: 4 dimes and
2 nickels?
50% of a dollar
40% of a dollar
60% of a dollar
Answers
4simes = 40 cents
2 nickles = 10 cnet’s
PLEASEEEEEEEEEE HELPPPPP MEEEEE!!!!!

Answers
Find the equations of the tangents to the curve x = 6t^2 + 4, y = 4t^3 + 4 that pass through the point (10, 8). y=?? (smaller slope)
y=?? (larger slope)
Answers
The equations of the tangents are:y = -3/2 + sqrt(37)/2(x - 10) (smaller slope)y = -3/2 - sqrt(37)/2(x - 10) (larger slope):y=-\frac{3}{2}+\frac{\sqrt{37}}{2}(x-10) (smaller slope)y=-\frac{3}{2}-\frac{\sqrt{37}}{2}(x-10) (larger slope).
Curve isx = 6t^2 + 4, y = 4t^3 + 4the slope of tangent of this curve dy/dx is dy/dx=12t/(3t^2+2)Then, equation of tangent with slope m and passing through (x1, y1) is given by(y - y1) = m(x - x1) ............(1)Here, point is (10,8)Therefore, equation of tangent passing through (10, 8) will be of the form(y - 8) = m(x - 10)Let this tangent intersect the curve at point P. Then, the coordinates of point P are given byx = 6t^2 + 4y = 4t^3 + 4.
Equating this with equation (1), we get:4t^3 + 4 - 8 = m(6t^2 - 6)4t^3 = 6m(t^2 - 1)2t^3 = 3m(t^2 - 1)2t^3 + 3mt - 3m = 0t = -m/2 ± sqrt(m^2/4 + 3m)Therefore, the two tangents are given by:y - 8 = m1(x - 10), where m1 = -3/2 + sqrt(37)/2y - 8 = m2(x - 10), where m2 = -3/2 - sqrt(37)/2Hence, the equations of the tangents are:y = -3/2 + sqrt(37)/2(x - 10) (smaller slope)y = -3/2 - sqrt(37)/2(x - 10) (larger slope):y=-\frac{3}{2}+\frac{\sqrt{37}}{2}(x-10) (smaller slope)y=-\frac{3}{2}-\frac{\sqrt{37}}{2}(x-10) (larger slope).
Learn more about slope tangent here:
https://brainly.com/question/32393818
#SPJ11
Which equation is equivalent to 9x+4y=16
Answers
Answer:
8x time 2x= 16
For the in parts A through E, choose the highest level of measurement (or cannot be determine).
A. Temperature of refrigerators ---
Nominal
Ratio
Cannot determine
Interval
Ordinal
B. Horsepower of race car engines ---
Ordinal
Interval
Nominal
Cannot determine
Ratio
C. Marital status of school board members ---
Interval
Nominal
Ordinal
Cannot determine
Ratio
D. Ratings of televisions programs (poor, fair, good, excellent) ---
Ordinal
nominal
Interval
Cannot determine
Ratio
E. Ages of children enrolled in a daycare
Ordinal
nominal
Interval
Cannot determine
Ratio
Answers
Temperature of refrigerators - Cannot determine. Horsepower of race car engines - Ratio. Marital status of school board members - Nominal. Ratings of television programs - Ordinal. Ages of children enrolled in a daycare - Interval
The level of measurement for the temperature of refrigerators cannot be determined based on the given information. The temperature could potentially be measured on a nominal scale if the refrigerators were categorized into different temperature ranges. However, without further context, it is not possible to determine the specific level of measurement.
The horsepower of race car engines can be measured on a ratio scale. Ratio scales have a meaningful zero point and allow for meaningful comparisons of values, such as determining that one engine has twice the horsepower of another.
The marital status of school board members can be measured on a nominal scale. Nominal scales are used for categorical data without any inherent order or ranking. Marital status categories, such as "married," "single," "divorced," etc., can be assigned to school board members.
The ratings of television programs, such as "poor," "fair," "good," and "excellent," can be measured on an ordinal scale. Ordinal scales represent data with ordered categories or ranks, but the differences between categories may not be equal or measurable.
The ages of children enrolled in a daycare can be measured on an interval scale. Interval scales have equal intervals between values, allowing for meaningful differences and comparisons. Age, measured in years or months, can be represented on an interval scale.
Learn more about nominal scale visit:
brainly.com/question/28465126
#SPJ11
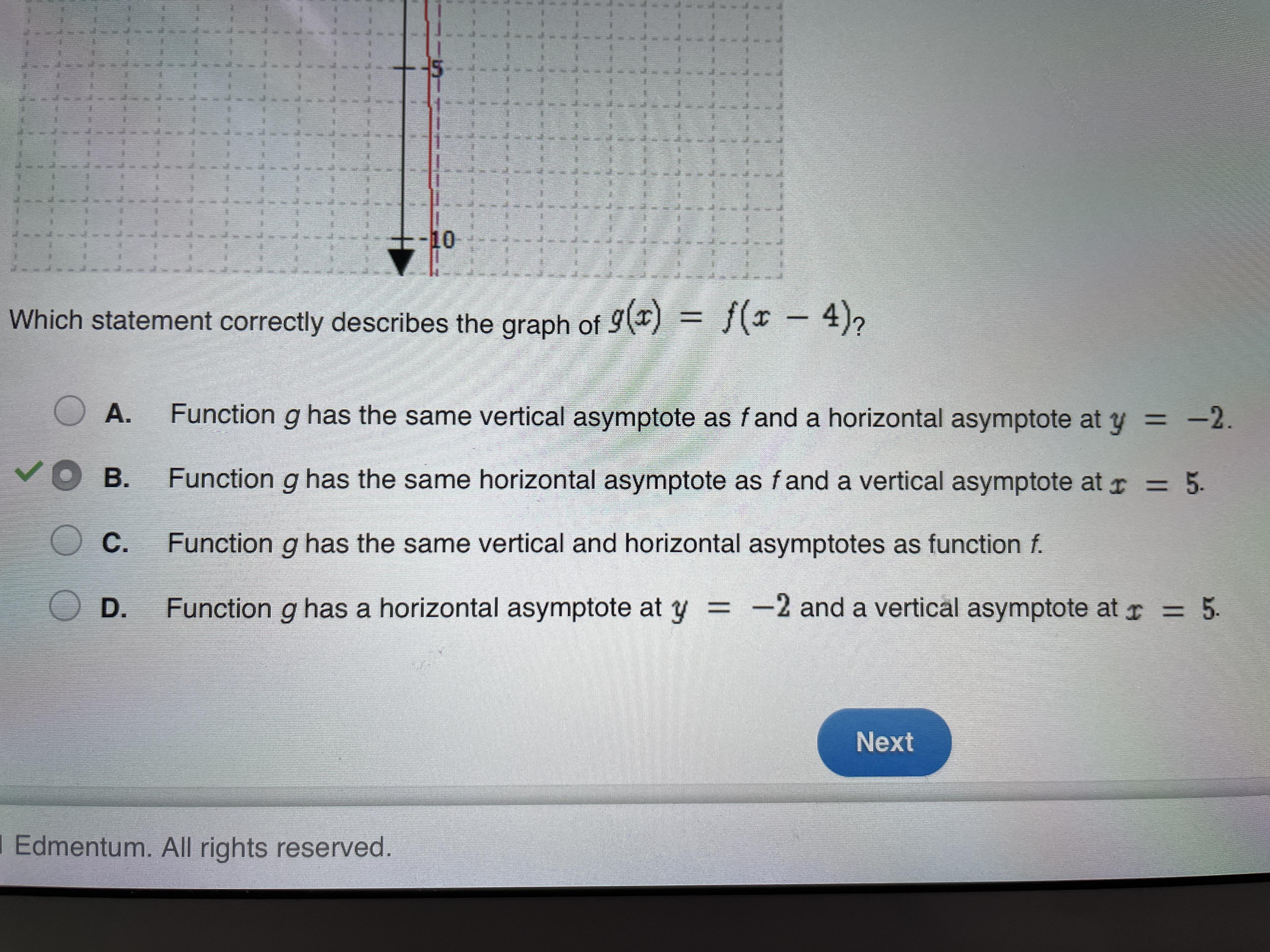
Which statement correctly describes the graph of g(x)=f(x-4)


Answers
Answer:
Option (B)
Step-by-step explanation:
From the graph attached,
If the parent function 'f' is shifted 4 units to the right,
g(x) = f(x- 4)
By shifting the parent function right vertical asymptote will come to x = 5 from x = 1.
Vertical asymptote y = 2 will remain same for the shifted function.
Therefore, function g(x) will have the asymptotes;
Vertical asypmtote: x = 5
Horizontal asymptote; y = 2
Therefore, Option (B) will be the correct option.
Answer: look at image
Step-by-step explanation:
Is the answer option c?

Answers
Answer:
No it isnt corret answer.
Answer: Choice D
Explanation:
Recall that the quadrants are labeled such that Q1 (shorthand for quadrant 1) is in the upper right corner. Then we have Q2 in the upper left corner. We work counterclockwise around as shown in the diagram below.
Therefore, the curve is found in Q1 and Q3

Which value of x is the solution of the equation 2(x – 4) + 7 = 3? (a) 1 (b) 6 (c) 2 (d) 0
Answers
Answer:
(c) 2
Step-by-step explanation:
2(x - 4) + 7 = 3
2x + 2(-4) + 7 = 3
2x - 8 + 7 = 3
2x - 1 = 3
2x - 1 + 1 = 3 + 1
2x = 4
2x/2 = 4/2
x = 2
Hope this helps!!!
The correct value of x is 2 in the given equation.
What is an equation?An equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =.
Given is an equation, 2(x – 4) + 7 = 3
Solving for x,
2(x – 4) + 7 = 3
2x-8+7 = 3
2x-1 = 3
2x = 4
x = 2
Hence, the value of x is 2.
For more references on equation, click;
https://brainly.com/question/29657983
#SPJ2
Which of the following triangles describes AA similarity?
Answers
The triangles AEB and DEC describes AA similarity .
What is AA Similarity ?
Two triangles are said to be congruent by AA Similarity when two angles in one triangle are congruent to two angles in another triangle .
In the question ,
a figure is given .
in triangle AEB and triangle DEC ,
we can see that ,
∠AEB ≅ ∠DEC , because they are vertically opposite angles .
On rotating triangle CED by 180° around the point E, then the translate point D to point A confirms ∠EAB ≅ ∠EDC.
Since two angles are Congruent
So , By AA Similarity , triangles AEB and DEC are Congruent .
Therefore , the triangles AEB and DEC are Congruent .
The given question is incomplete , the complete question is
Which of the following triangles in the given figure describes AA similarity ?
Learn more about Similarity here
https://brainly.com/question/27884002
#SPJ4
