A plastic pool gets filled up with 10L of water per hour.
a) After 2 hours how much water is in the pool? Write an equation.
b) After how many hours will the pool be 80L?
c) Is part b) linear or nonlinear?
Answers
a) The amount of water in the pool after 2 hours can be calculated using the equation.
Water in pool = 10L/hour × 2 hours = 20L.
b) The pool will be 80L when the equation is satisfied: 80L = 10L/hour × Time.
Solving for Time, we find Time = 8 hours.
c) Part b) is linear.
a) To calculate the amount of water in the pool after 2 hours, we can use the equation:
Water in pool = Water filling rate × Time
Since the pool gets filled up with 10L of water per hour, we can substitute the values:
Water in pool = 10 L/hour × 2 hours = 20L
Therefore, after 2 hours, there will be 20 liters of water in the pool.
b) To determine the number of hours it takes for the pool to reach 80 liters, we can set up the equation:
Water in pool = Water filling rate × Time
We want the water in the pool to be 80 liters, so the equation becomes:
80L = 10 L/hour × Time
Dividing both sides by 10 L/hour, we get:
Time = 80L / 10 L/hour = 8 hours
Therefore, it will take 8 hours for the pool to contain 80 liters of water.
c) Part b) is linear.
The equation Water in pool = Water filling rate × Time represents a linear relationship because the amount of water in the pool increases linearly with respect to time.
Each hour, the pool fills up with a constant rate of 10 liters, leading to a proportional increase in the total volume of water in the pool.
For similar question on amount.
https://brainly.com/question/25720319
#SPJ8
Related Questions
The Spanish Club is having a potluck lunch where each student brings in a cultural dish. The 10 students randomly draw cards numbered with consecutive integers from 1 to 10. Students who draw odd numbers will bring main dishes. Students who draw even numbers will bring desserts. If Cynthia is bringing a dessert, what is the probability that she drew the number 10?
Answers
Answer: The probability is 1/5
Step-by-step explanation: there are 5 even numbers in between 1 to ten and ten is one of them so it would be 1/5 probability hope this helps! :)
The requried probability that she drew the number 10 is 0.2.
What is probability?
Probability can be defined as the ratio of favorable outcomes to the total number of events.
Here,
There are 5 even numbers and 5 odd numbers in the set of integers from 1 to 10. Since Cynthia is bringing a dessert, she must have drawn an even number.
Therefore, the probability that she drew the number 10 is given as,
= 1/5 = 0.2
since there is only 1 even number that is greater than 8 (i.e., 10).
Thus, the probability that she drew the number 10 is 0.2.
Learn more about probability here:
brainly.com/question/14290572
#SPJ2
Hurry please!!
Which linear equation represents the graph?A) y=-3x - 2
B) y = 3x + 2
C) y=-1/3x+2
D) y= 1/3 x - 2

Answers
Answer:
A) y = -3x -2
Step-by-step explanation:
1. start at point (-1,1)
2. move down 3 (-3) and over to the right 1 (1)
3. that makes your slope -3/1 which is just -3.
4. find your y-intercept: -2
5. using y=mx+b, plug in your numbers and you get
6. y = -3x -2
Hope this helps! Brainliest, please!
What is the answer to this question?

Answers
Answer:
≈ 3.9 miles
Step-by-step explanation:
The third angle in the triangle is
180° - (53 + 78)° = 180° - 131° = 49°
Using the Sine rule in the triangle with distance from 2 being x, then
\(\frac{3}{sin49}\) = \(\frac{x}{sin78}\) ( cross- multiply )
x × sin49° = 3 × sin78° ( divide both sides by sin49° )
x = \(\frac{3sin78}{sin49}\) ≈ 3.9 ( to the nearest tenth )
In triangle EFG, m∠E = 69.7° and m∠F = 25.9°. Determine the measure of the exterior angle to ∠G.
43.8°
84.4°
110.3°
95.6°
Answers
The triangle EFG's exterior angle to G is 95.6 degrees.
What is Exterior Angle Theorem?The exterior angle theorem states that when a triangle's side is extended, the resultant exterior angle formed is equal to the sum of the measures of the two opposite interior angles of the triangle. The theorem can be used to find the measure of an unknown angle in a triangle.
So, Using Exterior angle theorem
We can say that
m∠E = 69.7°+ m∠F = 25.9° = exterior angle to ∠G
So,
exterior angle to ∠G = 69.7+25.9=95.6°
Therefore we can say that the Exterior angle to G of the triangle EFG is 95.6°.
Learn more about exterior angles here
https://brainly.com/question/28835566
#SPJ1
Help me please, help

Answers
Answer:
x>0
Step-by-step explanation:
HELP PLS MATH !!!!!!!!!!!!!!

Answers
fraction form : 8/25
decimal form : 0.32
Answer:
8/25 or if you have to do decimal form it's 0.32
Step-by-step explanation:
find area of the shaded part

Answers
Answer:
25.65634 squares cm
Step-by-step explanation:
The area of the whole circle is
pi x 7 squared
pix49 =153.93804
the degrees of a circle are 360
60 is 1/6 of 360
so we need to divide the area by 6
153.93804/6 = 25.65634
Events M and N are independent events.In this scenario, if P(M) = 0.23 and P(M and N) = 0.158, then P(N) = Round your answer to the nearest tenth.
Answers
Events M and N are independent events.
It means that the outcome of one event does not affect the outcome of the other event.
The probability of events M and N both occurring is given by
\(P(M\; \text{and}\; N)=P(M)\times P(N)\)Re-arranging for P(N), we get
\(P(N)=\frac{P(M\; \text{and}\; N)}{P(M)}\)Where
P(M and N) = 0.158
P(M) = 0.23
\(P(N)=\frac{P(M\; \text{and}\; N)}{P(M)}=\frac{0.158}{0.23}=0.7\)Therefore, the probability P(N) is 0.7
PLEASE HLEP WILL GIVE BRAINLIEST

Answers
Answer:
Question number 1: Correlation = no. Causation = no.
Question number 2: Correlation = yes. Causation = no.
Question number 3: Correlation = yes. Causation = yes.
Step-by-step explanation:
Happy to help!
look at cliped pic please help

Answers
Answer:
\(( { \frac{4}{7} )}^{2} = \frac{ {4}^{2} }{ {7}^{2} } = \frac{16}{49} \)
(c) A non-uniform but spherically symmetric charge distribution has a charge density: rho(r)=rho 0
(1−r/R)
rho(r)=0
for r≤R
for r>R
where rho 0
=3Q/πR 3
is a positive constant. Show that the total charge contained in this charge distribution is Q. [4] Show that the electric field in the region r>R is identical to that created by a point charge Q at r=0 [2] Derive an expression for the electric field in the region r≤R. [5]
Answers
To show that the total charge contained in the charge distribution is Q, we integrate the charge density over the entire volume. The charge density is given by:
ρ(r) = ρ₀(1 - r/R) for r ≤ R,
ρ(r) = 0 for r > R,
where ρ₀ = 3Q/πR³.
To find the total charge, we integrate ρ(r) over the volume:
Q = ∫ρ(r) dV,
where dV represents the volume element.
Since the charge density is spherically symmetric, we can express dV as dV = 4πr² dr, where r is the radial distance.
The integral becomes:
Q = ∫₀ᴿ ρ₀(1 - r/R) * 4πr² dr.
Evaluating this integral gives:
Q = ρ₀ * 4π * [r³/3 - r⁴/(4R)] from 0 to R.
Simplifying further, we get:
Q = ρ₀ * 4π * [(R³/3) - (R⁴/4R)].
Simplifying the expression inside the parentheses:
Q = ρ₀ * 4π * [(4R³/12) - (R³/4)].
Simplifying once more:
Q = ρ₀ * π * (R³ - R³/3),
Q = ρ₀ * π * (2R³/3),
Q = (3Q/πR³) * π * (2R³/3),
Q = 2Q.
Therefore, the total charge contained in the charge distribution is Q.
To show that the electric field in the region r > R is identical to that created by a point charge Q at r = 0, we can use Gauss's law. Since the charge distribution is spherically symmetric, the electric field outside the distribution can be obtained by considering a Gaussian surface of radius r > R.
By Gauss's law, the electric field through a closed surface is given by:
∮E · dA = (1/ε₀) * Qenc,
where ε₀ is the permittivity of free space, Qenc is the enclosed charge, and the integral is taken over the closed surface.
Since the charge distribution is spherically symmetric, the enclosed charge within the Gaussian surface of radius r is Qenc = Q.
For the Gaussian surface outside the distribution, the electric field is radially directed, and its magnitude is constant on the surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q,
Simplifying:
E = Q / (4πε₀r²).
This is the same expression as the electric field created by a point charge Q at the origin (r = 0).
To derive an expression for the electric field in the region r ≤ R, we can again use Gauss's law. This time we consider a Gaussian surface inside the charge distribution, such that the entire charge Q is enclosed.
The enclosed charge within the Gaussian surface of radius r ≤ R is Qenc = Q.
By Gauss's law, we have:
∮E · dA = (1/ε₀) * Qenc.
Since the charge distribution is spherically symmetric, the electric field is radially directed, and its magnitude is constant on the Gaussian surface. Hence, E · dA = E * 4πr².
Plugging these values into Gauss's law:
E * 4πr² = (1/ε₀) * Q.
Simplifying:
E = Q / (4πε₀r²).
This expression represents the electric field inside the charge distribution for r ≤ R.
Learn more about charge here:
https://brainly.com/question/18102056
#SPJ11
Noah and his grandfather were returning home from a walk. When they were 800 m away from the house, the grandfather said that he was thirsty. Noah immediately ran home, got a bottle of water, and ran back to meet his grandfather who never stopped walking at a steady pace. How many meters from the house did they meet if noah ran four times as fast as his grandfather walked.
PLEASE HELP!!!!! DUE IN 5 MIN!!!!!!!!! I GIVE BRAINLIEST AND POINTS!!!!
Answers
They met 480 meters from the house.
CalculusGiven that Noah and his grandfather were returning home from a walk, and when they were 800 m away from the house, the grandfather said that he was thirsty, so Noah immediately ran home, got a bottle of water, and ran back to meet his grandfather who never stopped walking at a steady pace, to determine how many meters from the house did they meet if noah ran four times as fast as his grandfather walked, the following calculation must be made:
200 x 4 = 800 - 200 = 600300 x 4 = 1200 - 800 - (800 - 300) = 100325 x 4 = 1300 - 800 - (800 - 325) = -25320 x 4 = 1280 - 800 - (800 - 320) = 480 - 480 = 0Therefore, they met 480 meters from the house.
Learn more about calculus in https://brainly.com/question/26453068
1. Let D = Zli be the ring of Gaussian integers. We know that D is an Euclidean domain with measure dm + in) = m + n. For x = 3+2i and y = 2-5i, produce 4,7 E D such that = q + r and d(r)
Answers
The Euclidean algorithm can be applied to Gaussian integers in the same way it is applied to ordinary integers. In this case, we are given x = 3+2i and y = 2-5i and we need to find q and r such that x = qy + r and d(r) < d(y).
First, we divide x by y to get a quotient and remainder:
x/y = (3+2i)/(2-5i) = (3+2i)(2+5i)/(2-5i)(2+5i) = (16+7i)/29 = 0.551724 + 0.241379i
Since q and r must be Gaussian integers, we round the real and imaginary parts of the quotient to the nearest integer to get q = 1 + 0i = 1.
Next, we multiply q by y and subtract from x to get the remainder:
r = x - qy = (3+2i) - (1)(2-5i) = 1+7i
Finally, we check that d(r) < d(y):
d(r) = 1^2 + 7^2 = 50
d(y) = 2^2 + (-5)^2 = 29
Since d(r) > d(y), we need to adjust our quotient and remainder. We can do this by subtracting 1 from the real part of q and adding y to the remainder:
q = 0 + 0i = 0
r = (1+7i) + (2-5i) = 3+2i
Now, d(r) = 3^2 + 2^2 = 13 < 29 = d(y), so our final answer is q = 0 and r = 3+2i.
For more such questions on Euclidean algorithm.
https://brainly.com/question/12930118#
#SPJ11
The average temperature in Long Beach California is 80 degrees Fahrenheit with a standard deviation of 3 degrees. What percentage of temperatures fall between 80 and 89 degrees?
Answers
Answer:
0.4987
Step-by-step explanation:
What we must do is calculate the z value for each value and thus find what percentage each represents and the subtraction would be the percentage between those two values.
We have that z is equal to:
z = (x - m) / (sd)
x is the value to evaluate, m the mean, sd the standard deviation
So for 80 we have:
z = (80 - 80) / (3)
z = 0
and this value represents 0.5
for 89 we have:
z = (89 - 80) / (3)
z = 3
and this value represents 0.9987
we subtract:
0.9987 - 0.5 = 0.4987
Which means that it represents 49.87%

Kayla has just subscribed to a music streaming service. For a one-time fee of $12.99, she can download songs for $0.65 each, for an entire month. Kayla's budget will allow her to spend no more than a total of $27 on the streaming service this month. What is the maximum number of songs she can download while still remaining within her budget?
a) x <= 22
b) <= 41
c) x <= 21
d) X <= 42

Answers
The maximum number of songs she can download while still remaining within her budget is x <= 21
How to determine the maximum number of songs?The given parameters are:
One-time fee = $12.99
Rate = $0.65 per song
Budget = $27
The inequality is then represented as:
One-time fee + Rate * x <= Budget
So, we have:
12.99 + 0.65x <= 27
Subtract 12.99 from both sides
0.65x <= 14.01
Divide both sides by 0.65
x <= 21.55
Round down
x <= 21
Hence, the maximum number of songs she can download while still remaining within her budget is x <= 21
Read more about inequality at:
https://brainly.com/question/25275758
#SPJ1
13. A company is buying new computers. The company needs no more than 220 desktops and at
least 50 laptops. A total of at least 200 computers must be bought. Write a system of linear
inequalities to represent the constraints of this situation. Let x represent the number of desktops
and let y represent the number of laptops,
Answers
The system of linear inequalities to represent the constraints of this situation is x + y ≥ 200, x ≤ 220, y ≥ 50.
This means that the total number of computers (desktop plus laptops) must be at least 200 (x + y ≥ 200). The company needs no more than 220 desktops (x ≤ 220), and at least 50 laptops (y ≥ 50).
The inequality x + y ≥ 200 represents the total number of computers needed, x ≤ 220 represents the maximum number of desktops needed, and y ≥ 50 represents the minimum number of laptops needed. Together, these inequalities represent the constraints of the situation.
For more questions like Desktops click the link below:
https://brainly.com/question/17925522
#SPJ4
What is 0.18 divided by 7.56 plzz help me and the others ones to

Answers
Answer:
0.023
Step-by-step explanation:
The candy shop made 3/18 pounds of chocolate they sold 1 pounds how many pounds of chocolate do they have left
Answers
The question is incomplete. Please see the complete question below
The candy shop made 3 1/18 pounds of chocolate they sold 1 1/4pounds how many pounds of chocolate do they have left
Answer:
15/8
Step-by-step explanation:
The shop made 3 1/8 pound of chocolate
They sold 1 1/4 of chocolates
Hence the number of chocolates left can be calculated as follows
3 1/8-1 1/4
= 25/8-5/4
= 15/8
I need help fast plss

Answers
The measures of the angles are ∠1 = 127°, ∠2 = 53°, ∠3 = 127°, ∠4 = 37°, ∠5 = 53°, ∠6 = 90°, ∠7 = 37°, ∠8 = 143°, ∠9 = 37° and ∠10 = 143°
Finding the measures of the anglesFrom the question, we have the following parameters that can be used in our computation:
The transversal lines and the other lines
So, we have
∠1 = 180 - 53
Evaluate
∠1 = 127°
Also, we have
∠5 = 53°
By vertical angles, we have
∠2 = 53°
∠3 = 127°
Next, we have
∠4 = 127 - 90°
∠4 = 37°
Solving further, we have
∠6 = 90°
By corresponding angles, we have
∠7 = 37°
∠9 = 180 - 90 - 53°
∠9 = 37°
∠10 = 90 + 53°
∠10 = 143°
∠8 = 143°
Read more about angles at
https://brainly.com/question/28293784
#SPJ1
Help please! The question is on the picture. Thanks!

Answers
Which expression is equivalent to P/6 +(q+8)
Answers
Which expressions are equivalent to -2(2h+10)+4h
Answers
combine like terms that equals zero
so 20 is your answer
When forecasting induced seismicity hazard, researchers use parameters like rock properties and injection rates to calculate what?.
Answers
Different models and methodologies exist, and ongoing research aims to improve our understanding and ability to predict and manage induced seismicity hazards.
Different models and methodologies exist, and ongoing research aims to improve our understanding and ability to predict and manage induced seismicity hazards.
When forecasting induced seismicity hazard, researchers use parameters like rock properties and injection rates to calculate the likelihood and magnitude of induced earthquakes. These parameters are important factors that influence the response of the subsurface to fluid injection or extraction activities, such as hydraulic fracturing (fracking) or fluid disposal in deep wells.
Here are some specific calculations researchers might perform using these parameters:
1. Seismicity Rate: Researchers estimate the rate at which induced earthquakes may occur by analyzing the injection rates of fluids (e.g., water, wastewater, or hydraulic fracturing fluids) into the subsurface.
The higher the injection rate, the greater the likelihood of inducing seismic activity.
2. Magnitude-Frequency Distribution: Researchers analyze the rock properties, including its stress state, fault network, and fault stability, along with the injection rates, to estimate the magnitude and frequency of induced earthquakes.
They use statistical models, such as the Gutenberg-Richter relationship, to predict the distribution of earthquake magnitudes that may occur due to the injection activities.
3. Stress Changes: Injection activities can alter the stress distribution within the subsurface, potentially leading to fault activation or slip.
Researchers assess the rock properties, including the in-situ stress conditions, to calculate the stress changes induced by fluid injection. This information helps determine the potential for fault reactivation and the magnitude of induced seismic events.
4. Seismic Hazard Maps: By combining the above calculations with geologic and geophysical data, researchers can create seismic hazard maps that indicate the areas at higher risk of induced earthquakes.
These maps provide valuable information for regulatory bodies, industry stakeholders, and decision-makers to mitigate potential risks associated with fluid injection or extraction operations.
To know more about hydraulic fracturing click-
https://brainly.com/question/32112456
#SPJ11
The overnight low temperature in Cassidy City was -27 Fahrenheit. The overnight low temperature in Shakerville was -6 Fahrenheit. How much warmer was shakerville than Cassidy City?
Answers
Answer:
Shakerville 21° warmer
Step-by-step explanation:
-27 + -6 = 21
2. Suppose z is a function of x and y and tan (√x + y) = e²². Determine z/х and z/y . 3. Let z = 2² + y³, x=2 st and y=s-t². Compute for z/х and z/t
Answers
Suppose z is a function of x and y and tan (√x + y) = e²², we get:`z/t = -12st³ + 12s²t⁴`Therefore, `z/t = -12st³ + 12s²t⁴`.
To find z/x, differentiate z with respect to x and keep y constant. `z/x = dz/dx * dx/dx + dz/dy * dy/dx` (Note that `dx/dx` = 1)Now, `dz/dx = -((√x + y)⁻²)/2√x` by the chain rule. Also, we know that `tan (√x + y) = e²²`.
Therefore, `tan (√x + y)` is a constant. Hence,`dz/dx = 0`.Therefore, `z/x = 0`.To find z/y, differentiate z with respect to y and keep x constant. `z/y = dz/dx * dx/dy + dz/dy * dy/dy` (Note that `dx/dy = 0` as x is a constant)
Differentiating z with respect to y, we get:`dz/dy = 3y²`Therefore,`z/y = 3y²`3. Let z = 2² + y³, x = 2 st and y = s - t². Compute for z/х and z/t
To find z/x, differentiate z with respect to x and keep y constant. `z/x = dz/dx * dx/dx + dz/dy * dy/dx` (Note that `dx/dx` = 1)
Now, `dx/dx = 1` and `dz/dx = 0` because z does not depend on x.
Hence, `z/x = 0`.To find z/t, differentiate z with respect to t and keep x and y constant.` z/t = dz/dt * dt/dt` (Note that `dx/dt = 2s`, `dy/dt = -2t`, `dx/dt` = `2s`)
Differentiating z with respect to t, we get:`dz/dt = 3y² * (-2t)`
Substituting x = 2st and y = s - t², we get: `z/t = 3(s - t²)²(-2t)`
Simplifying, we get: `z/t = -12st³ + 12s²t⁴`
Therefore, `z/t = -12st³ + 12s²t⁴`.
More on functions: https://brainly.com/question/30480002
#SPJ11
PLEASE I NEED HELP FIND THE X USE THE SCREEN SHOT

Answers
trigonometry, please help.

Answers
The value of x is given as follows:
x = 9.40 cm.
What are the trigonometric ratios?The three trigonometric ratios are the sine, the cosine and the tangent, and they are defined as follows:
Sine of angle = length of opposite side to the angle divided by the length of the hypotenuse.Cosine of angle = length of adjacent side to the angle divided by the length of the hypotenuse.Tangent of angle = length of opposite side to the angle divided by the length of the adjacent side to the angle.The parameters for this problem are given as follows:
Hypotenuse of 10 cm.Side length of x cm adjacent to the angle of 20º.Applying the cosine, the value of x is obtained as follows:
cos(20º) = x/10
x = 10 x cosine of 20 degrees
x = 9.40 cm.
More can be learned about trigonometric ratios at brainly.com/question/24349828
#SPJ1
Greg went to Bed Bath and Beyond to buy Christmas gifts for his family this year. In his first trip he bought 4 candles, 5 wallflowers, and 6 lotions for a total of $123. Greg forgot some people on his list the first time so he makes a second trip and spent $48 to buy 2 candles, 3 wallflowers, and 1 lotion. The price of a lotion is 2 less than 2 times the price of a wallflower. How much does each item cost?
Answers
Answer:
Price of Candle: 12.5
Price Wallflower: 5
Price of Lotion: 8
Step-by-step explanation:
Let cost of a candle = \(x\)
Let cost of a wallflower = \(y\)
Let cost of a lotion = \(z\)
Cost of 4 candles = 4\(x\)
Cost of 5 wallflowers = 5\(y\)
Cost of 6 lotions = 6\(z\)
Cost of 2 candles = 2\(x\)
Cost of 3 wallflowers = 3\(y\)
Cost of 1 lotion = \(z\)
As per question statement:
\(4x+5y+6z=123 .... (1)\\2x+3y+z=48 ...... (2)\\z=2y-2 ..... (3)\)
Using equation (3) in (1) and (2), the equations get reduced to :
\(\Rightarrow 4x+17y = 135 ..... (4)\\\Rightarrow 2x+5y = 50 ..... (5)\)
Multiplying (5) with 2 and subtracting from equation (1):
\(7y = 35\\\Rightarrow y = 5\)
By equation (3):
\(\Rightarrow z =8\)
By equation (4):
\(\Rightarrow x = 12.5\)
Therefore, the answer is:
Price of Candle: 12.5
Price Wallflower: 5
Price of Lotion: 8
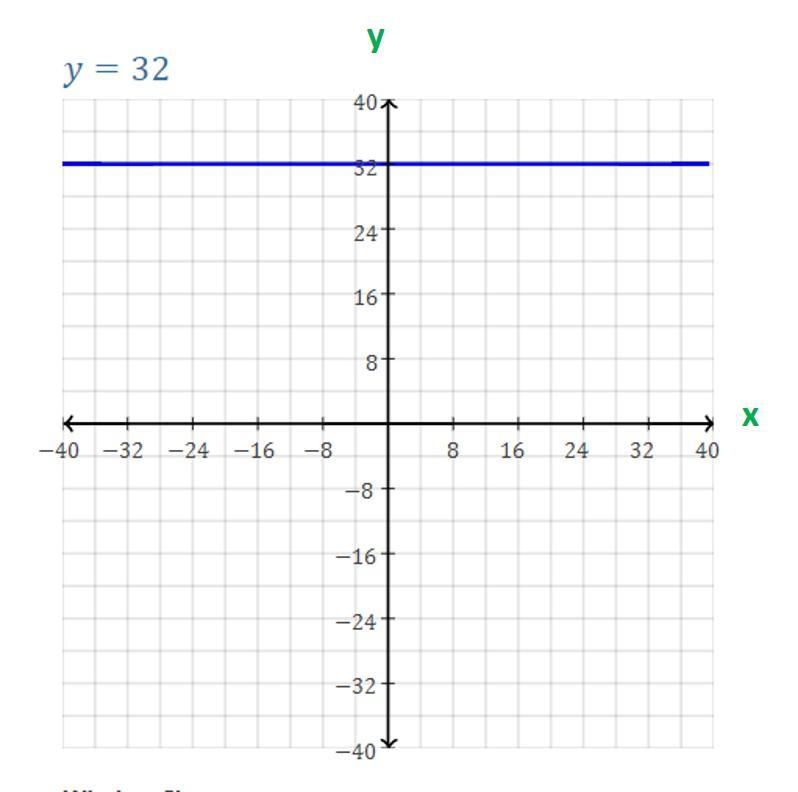
Graph the function f(x) = 32. Plot the key features including any x- and y-intercepts, any vertical, horizontal, or slant asymptotes, and any holes.
Answers
The graph of the function f(x) = 32 is attached accordingly.
How would you describe the above graph ?X - Intercept - There is no x-intercept since the function is a horizontal line.
Y -Interept - The y-intercept is (0, 32), since the line intersects the y-axis at y = 32.
Vertical Asymptotes - There are 0 vertical asymptotes, since t function is defined for all values of x.
Horizontal Asymptotes - There are 0 horizontal asymptotes, since the function is a horizontal line.
Slant Asymptotes - There are zeroslant asymptotes, since the function is a horizontal line.
Holes - There are zeroholes in the graph, since the function is a horizontal line with no breaks or discontinuities.
Learn more about graphs:
https://brainly.com/question/17267403
#SPJ1
Answer: see below
Step-by-step explanation:
got it right on quiz

Now check your predictions. In GeoGebra, rotate quadrilateral ABCD about the origin through angles of 90°, 180°, 270°, and 360°. Enter the coordinates of the vertices of quadrilateral A′B′C′D′ in the table. Paste a screen capture of the images you created below the table.

Answers
Answer:
Plato answer.

Answer:
(−3, −2) (−2, −1) (−1, −2) (−1, −4)
Angle of Rotation (CCW)
90° (2, −3) (1, −2) (2, −1) (4, −1)
180° (3, 2) (2, 1) (1, 2) (1, 4)
270° (−2, 3) (−1, 2) (−2, 1) (−4, 1)
360° (−3, −2) (−2, −1) (−1, −2) (−1, −4)