A party planner organized a dinner party. The party planner recorded the height of the candlesticks over time and graphed the relationship. graph with the x axis labeled time in hours and the y axis labeled height of candlestick in inches and a line going from the point 0 comma 9 through the point 3 comma 7 Find and interpret the slope and y-intercept in this real-world situation. The slope is negative two thirds, and the y-intercept is 9. The candle starts at a height of 9 inches and decreases two thirds of an inch every hour. The slope is negative three halves, and the y-intercept is 9. The candle starts at a height of 9 inches and decreases three halves of an inch every hour. The slope is 9, and the y-intercept is negative two thirds. The candle starts at a height of two thirds of an inch and decreases 9 inches every hour. The slope is 9, and the y-intercept is negative three halves. The candle starts at a height of three halves of an inch and decreases 9 inches every hour.
Answers
The slope and the y intercepts of the given graph which shows height of the candlesticks over time is :
Slope = -2/3
Y intercept = 9
The graph is that of the height of the candlesticks over time.
The line passes through two points (0, 9) and (3, 7).
Slope of the line can be calculated as,
Slope = (7 - 9) / (3 - 0) = -2/3
Hence the slope id negative two thirds.
y intercept of a graph is the y coordinate of the point where the line touches the Y axis.
The x coordinate will be 0 there.
The line passes through (0, 9).
So y intercept = 9
Hence the slope and the y intercept are -2/3 and 9 respectively.
Learn more about Slope here :
https://brainly.com/question/30216543
#SPJ1
Related Questions
find the points on the curve where the tangent is horizontal or vertical x=cos theta
Answers
The points on the curve where the tangent is horizontal: (1, 0) & (-1, 0), and where the tangent is vertical: (0, 1) & (0, -1)
How to find points on the curve?To find the points on the curve x=cos(theta) where the tangent is horizontal or vertical, we need to find the derivative of x with respect to theta.
Taking the derivative of x with respect to theta, we get:
dx/dtheta = -sin(theta)
When the tangent is horizontal, the derivative is equal to zero. So we need to solve the equation -sin(theta) = 0 for theta.
This equation is true when theta = n*pi, where n is an integer. So the points on the curve x=cos(theta) where the tangent is horizontal are:
(1, 0) for n=2k, where k is an integer
(-1, 0) for n=2k+1, where k is an integer
When the tangent is vertical, the derivative is undefined. This happens when cos(theta) = 0, which is true when theta = (2k+1)*pi/2, where k is an integer.
So the points on the curve x=cos(theta) where the tangent is vertical are:
(0, 1) for n=2k+1, where k is an integer
(0, -1) for n=2k, where k is an integer
Therefore, the points on the curve where the tangent is horizontal are (1, 0) and (-1, 0), and the points on the curve where the tangent is vertical are (0, 1) and (0, -1).
Learn more about points on the curve
brainly.com/question/28715687
#SPJ11
C) if two individuals are chosen at random from the population, what is the probability that at least one will have some college or a college degree of some sort?
Answers
The probability that neither of the two individuals has some college or a college degree is (1 - P(college))^2.
To calculate the probability that at least one of the two individuals chosen at random from the population will have some college or a college degree, we need to consider the complement of the event, which is the probability that none of the individuals have a college degree.
Let's assume that the population size is N, and the number of individuals with a college degree is C. The probability that an individual does not have a college degree is (N - C) / N.
When choosing the first individual, the probability that they do not have a college degree is (N - C) / N.
When choosing the second individual, the probability that they do not have a college degree is also (N - C) / N.
Since these events are independent, we can multiply the probabilities together:
P(no college degree for either individual) = (N - C) / N * (N - C) / N = (N - C)² / N².
Now, to find the probability that at least one of the individuals has a college degree, we subtract the probability of none of them having a college degree from 1:
P(at least one with a college degree) = 1 - P(no college degree for either individual) = 1 - (N - C)² / N².
For more such question on probability. visit :
https://brainly.com/question/251701
#SPJ8
Find three numbers whose sum is 26, if the first number is three times the difference between the second and the third, and the second number is two more than twice the third. Solve the problem using matrices. The first number is the second is (Type an integer or a fraction.) and the third is .
Answers
The numbers whose sum is 26 are 15, 3, 8 .
Given data of matrix ,
First number is three times the difference between the second and the third.
The second number is two more than twice the third.
Now according to the given data,
Let the three numbers be x, y , z.
Then,
x = 3(y-z).......(1)
y = 2 + 2z
z = z
So,
The summation of all the three numbers is 26, then
3(y-z) + 2 + 2z + z = 26
z = 3
Substitute the value of z in 2,
y = 8
Substitute the value of y and z i 1,
x = 15.
Hence the values are:
x= 15
y = 8
z = 3
Know more about matrix,
https://brainly.com/question/28097317
#SPJ4
Determine the measure of the interior angle at vertex F

Answers
Answer:
72
Step-by-step explanation:
The interior angles of a 6 sided figure add to (n-2) * 180
where n is the number of sides
(6-2) *180
4*180
720
2x+4x+4x+4x+4x+2x = 720
20x = 720
Divide by 20
20x/20 = 720/20
x =36
We want <F
<F = 2x = 2*36 = 72
The ratio of the length of the toucan’s bill to the length of its body is 1 inch to 3.5 inches. If the bill is 7 inches, how long is the body?
Answers
Answer:
24.5 inches
Step-by-step explanation:
The ratio of the length of the toucan’s bill to the length of its body can be expressed as
(1: 3.5)
Then if the bill is 7 inches, then the Length of the body will be X
1: 3.5
7: X
If we cross multiply, we have
X= 7×3.5
X= 24.5
Hence, the Length of the body is 24.5 inches
7. Which piece of information differentiates a square from a rectangle?
A. The diagonals bisect each other.
B. All sides are equal in length.
C. Opposite sides are congruent.
D. All angles measure 90°.
Answers
Answer:
The answer is B. For rectangle, the sides have different lengths.
The rest of the options, applies to all squares and rectangles.
function extanx−1=0. 3.35 Find the real root of the equation x−sinx−0.25=0 to three significant digits using the Successive Approximation method. 3.36 Use the method of Successive Approximation to find a root of the equation ex−3x=0 in the interval
Answers
The real root of the equation x - sin(x) - 0.25 = 0, obtained using the Successive Approximation method, is approximately x = 0.732.
The Successive Approximation method is an iterative numerical technique used to approximate the roots of an equation. In this case, we are solving the equation x - sin(x) - 0.25 = 0 to three significant digits.
Step 1: Start with an initial guess for the root, let's say x0 = 0.
Step 2: Substitute x0 into the equation to calculate the next approximation, x1, using the formula x1 = sin(x0) + 0.25.
Step 3: Repeat step 2, using x1 as the new approximation, until the desired level of accuracy is achieved.
By applying the Successive Approximation method, we iterate the calculations and obtain the following results:
x1 = sin(0) + 0.25 = 0 + 0.25 = 0.25
x2 = sin(0.25) + 0.25 ≈ 0.247
x3 = sin(0.247) + 0.25 ≈ 0.248
x4 = sin(0.248) + 0.25 ≈ 0.248
x5 = sin(0.248) + 0.25 ≈ 0.248
After five iterations, we reach a value of x = 0.248, which is the real root of the equation x - sin(x) - 0.25 = 0 to three significant digits.
Learn more about real root.
brainly.com/question/21664715
#SPJ11
Evaluate the exponential expression. 14^2
Answers
Answer:196
Step-by-step explanation:
Answer:
196
Step-by-step explanation:
Exponential expressions are just a way to write powers in short form. The exponent indicates the number of times the base is used as a factor. So in the case of 32, it can be written as 2 × 2 × 2 × 2 × 2=25, where 2 is the “base” and 5 is the “exponent”. We read this expression as “two to the fifth power”.
Using the inverse of a matrix solve the following system of equations. Give your answer as an ordered pair.

Answers
In order to solve this system using the inverse of a matrix, first let's put the system in the matrix form:
\(\begin{gathered} \begin{cases}3x+7y=-4 \\ -x-y=2\end{cases} \\ \begin{bmatrix}{3} & {7} & \\ {-1} & {-1} & {}\end{bmatrix}\cdot\begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{-4} \\ {2}\end{bmatrix} \end{gathered}\)Now the system is in the form AX = B, where A, X and B are matrices.
To solve this system, we can do the following:
\(\begin{gathered} AX=B \\ A^{-1}\cdot AX=A^{-1}\cdot B \\ X=A^{-1}\cdot B \end{gathered}\)So we need to calculate the inverse matrix of A. We can do this as follows:
\(\begin{gathered} A^{-1}=\frac{1}{|A|}\cdot_{}\begin{bmatrix}{d} & {-b} & \\ {-c} & {a} & {}\end{bmatrix} \\ A=\begin{bmatrix}{3} & {7} & \\ {-1} & {-1} & {}\end{bmatrix}\to a=3,b=7,c=-1,d=-1 \\ |A|=a\cdot d-b\cdot c=-3-(-7)=4 \\ A^{-1}=\frac{1}{4}\cdot\begin{bmatrix}{-1} & {-7} & \\ {1} & {3} & {}\end{bmatrix}=\begin{bmatrix}{-\frac{1}{4}} & {-\frac{7}{4}} & \\ {\frac{1}{4}} & {\frac{3}{4}} & {}\end{bmatrix} \end{gathered}\)Now we have:
\(\begin{gathered} X=A^{-1}\cdot B \\ \begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{-\frac{1}{4}} & {-\frac{7}{4}} & \\ {\frac{1}{4}} & {\frac{3}{4}} & {}\end{bmatrix}\cdot\begin{bmatrix}{-4} \\ {2}\end{bmatrix} \\ \begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{-\frac{1}{4}\cdot(-4)+(-\frac{7}{4})\cdot2} \\ {\frac{1}{4}\cdot(-4)+\frac{3}{4}\cdot2}\end{bmatrix}=\begin{bmatrix}{-2.5} \\ {0.5}\end{bmatrix} \end{gathered}\)So the solution of this system is x = -2.5 and y = 0.5
State what additional information is required in order to know that the triangles are congruent for the reason given.
MULTIPLE CHOICE
refer to attachment
I WILL GIVE BRAINLIEST! PLS HELP!

Answers
Answer:
B) PQ ≅ VRStep-by-step explanation:
Reason given:
SAS, side-angle-sideRequired information:
Two sides and the included angleInformation given:
∠RQP ≅ ∠QRVQR ≅ RQ, same sideAddition information needed, the other side, adjacent to given angle:
PQ ≅ VRA rectangle that is 2 inches by 3 inches has been scaled by a factor of 7. 1.What are the side lengths of the scaled copy? 2. Suppose you want to scale the copy back to its original size. What scale factor should you use?
Answers
Which set of coordinates satisfies the equations x - 2y = -1 and 2x + 3y = 12?6541-6-5-4-3-2- 1123456-1-2-3-4-5-6
Answers
Given data:
The given equations are x - 2y = -1 and 2x + 3y = 12.
The given point of intersection is the solution of the equation which is (3, 2).
Thus, the solution of the given equations is (3, 2).
Aaron has 47 m of fencing to build a three-sided fence around a rectangular plot of land that sits on a riverbank. (The fourth side of the enclosure would be the river.) The area of the land is 266 square meters. List each set of possible dimensions (length and width) of the field.
Answers
The possible dimensions (length and width) of the field are:(10 m × 13 m) or (13 m × 10 m) and (11 m × 12 m) or (12 m × 11 m).
Given that Aaron has 47m of fencing to build a three-sided fence around a rectangular plot of land that sits on a riverbank. The fourth side of the enclosure would be the river.
The area of the land is 266 square meters.To find the possible dimensions (length and width) of the field, we can use the given information.The length of fencing required = 47 m.
Since the fence needs to be built on three sides of the rectangular plot, the total length of the sides would be 2l + w = 47.1. When l = 10 and w = 13, we have:
Length of the field, l = 10 m Width of the field, w = 13 mArea of the field = l × w = 10 × 13 = 130 sq. m2. When l = 11 and w = 12,
we have:Length of the field, l = 11 m
Width of the field, w = 12 m
Area of the field = l × w = 11 × 12 = 132 sq. m
To learn more about : dimensions
https://brainly.com/question/28107004
#SPJ8
The floor of Tatiana's basement has the dimensions shown.
7.25 yd
9.5 yd
15.5 yd
4.25 yd
What is the area of the basement floor? Round to the nearest hundredth if necessary.
Answers
After answering the presented question, we can conclude that Rounded area to the closest tenth, the basement floor area is 147.25 square yards
What is area?The size of a surface area can be expressed as an area. The surface area is the area of an open surface or the boundary of a three-dimensional object, whereas the area of a planar region or planar region refers to the area of a shape or flat layer. The area of an object is the entire amount of space occupied by a planar (2-D) surface or shape. Make a square with a pencil on a piece of paper. A two-dimensional character. On paper, the area of a shape is the amount of space it takes up. Assume the square is made up of smaller unit squares.
To calculate the size of the basement level, multiply the length and width of the rectangular floor by two. We can see from the measurements that the length is 15.5 yards and the width is 9.5 yards.
As a result, the basement floor area is:
Area = length x breadth = 15.5 yards x 9.5 yards
147.25 square yards is the area.
Rounded to the closest tenth, the basement floor area is 147.25 square yards.
To know more about area visit:
https://brainly.com/question/13194650
#SPJ1
Find the reciprocal of I
Answers
Answer:
the reciprocal of 1 is 1
Step-by-step explanation:
1/1 flipped is still equal to 1
because 1/1 flipped is still 1
Hello people ~
find the area of a circle with radius 13 m .
Answers
Answer:
Area of a circle
=πr^2
therefore...
radius r =13
but π =22/7
so..
=22/7 × 13^2
=22/7 ×169
=531.14m
Area of circle
πr²π(13)²169π530.66m²reflection over the y-axis followed by a horizontal translation 1 unit left on the equation f(x)=x
Answers
Answer:
f(x) = -x -4 or f(x) = (-x)-4
Step-by-step explanation:
Let the graph of g be a translation of 4 units down followed by a reflection in the y-axis of the graph of f(x)=x. Write a rule for g.
Transformations can be found using this general formula: f(x) = a(bx-h)+k
For this question, we want a translation down as well as a reflection.
The two values we need to use are for k, a vertical translation, and b, a reflection over the y-axis.
Since we are translating down 4 units, k = -4
Since we are reflecting across the y-axis, b = -1
So, f(x)=(-x)-4
or
f(x)= -x -4
In a shop the price of a radio is reduced by one third. if the original price of the radio is two thousand four hundred naira,what is the reduced price
Answers
If the original price of the radio is 2,400 Naira and it is reduced by one third, then the discounted price is 1,600 Naira.
A store usually provides discount of some items to attract more customers and make greater sales.
Suppose the original price is p, the discount rate is d%, and the discounted price is q, then the discounted price can be calculated as:
q = (1 - d%) x p
Parameters given in the problem:
p = 2,400 Naira
d = 1/3
Hence,
q = (1 - 1/3) x 2400
q = 2/3 x 2400 = 1600
Learn more about discount here:
https://brainly.com/question/1153322
#SPJ4
what is 2 + 1 kindergarten mathematics
Answers
Answer:
2 + 1 = 3
Step-by-step explanation:
You have 2 toy cars in your possession, and a friend gives you 1 more, now you have 3.
Hope this was the answer you were looking for.
:)
Solve for the value of pp (3p+6)° (4p+7)°
Answers
The value of the equation 6 + 3p = 4p + 7 is 1
How to solve the equation?Reorder the terms:
6 + 3p = 7 + 4p
Solving for the value of p by collecting like terms
6 + 3p = 7 + 4p
Move all terms containing p to the left, all other terms to the right.
Add '-4p' to each side of the equation.
-6 + 3p + -4p = -7 + 4p + -4p
Combine like terms: 3p + -4p = -1p
-6 + -1p = -7 + 4p + -4p
Combine like terms: 4p + -4p = 0
-6 + -1p = -7 + 0
-6 + -1p = -7
Add '6' to each side of the equation.
-6 + 6 + -1p = -7 + 6
Combine like terms: -6 + 6 = 0
0 + -1p = -7 + 6
-1p = -7 + 6
Combine like terms: -7 + 6 = -1
-1p = -1
Divide each side by '-1'.
p = 1
Simplifying
p = 1
Learn more about equations on https://brainly.com/question/29657992
#SPJ1
Solve for x - (4x-5y) = (-5y+4)
Answers
Answer:
X= 10/3y + -4/3
Step-by-step explanation:
Step One: add -5y to both sides
Step two: divide both sides by -3
Answer:
-x=1 1/3
Step-by-step explanation:
x-(4x-5y)=(5y+4)
x-4x+5y=5y+4
-3x+5y=5y+4
5y-5y=0
-3x=4
x=4÷3
4÷3=1 1/3
i need answers to b and c ASAP this i due tomorrow please label which is b and c


Answers
First, we have to find the t value in Jumel’s equation that will get him $75. So our equation is 75=60+0.05t. Then solve for your t value (subtract 60 from each side, divide by 0.05). You should get 300 as your t value. After this, just plug 300 into Ashley’s equation to find the cost. Your answer should be $150
Part C: Because both the equations are linear, both plans will cost the same at the point of intersection on a graph. This is where a certain t value for equation will produce the same c value, or cost
Pls help 10 points + Brainliest
Challenge 5-Exp
Enter the equation for the dotted exponential graph!

Answers
The exponential function for this problem is defined as follows:
y = 0.5(2/3)^x + 2.
How to define the exponential function?An exponential function is defined as follows:
y = a(b)^x + c.
In which:
a is used to find the value of y when x = 0.b is the rate of change.c is the horizontal asymptote.From the graph of the function, the horizontal asymptote is at y = 2, hence the parameter c is given as follows:
c = 2.
When x increases by 1, y is multiplied by 2/3, hence the parameter b is given as follows:
b = 2/3.
When x = 0, y = 2.5, hence the parameter a is obtained as follows:
a + c = 2.5.
a + 2 = 2.5
a = 0.5.
Meaning that the function is defined as follows:
y = 0.5(2/3)^x + 2.
More can be learned about exponential functions at https://brainly.com/question/30113628
#SPJ1
Polygon C CC has an area of 40 4040 square units. Kennan drew a scaled version of Polygon C CC using a scale factor of 1 2 2 1 start fraction, 1, divided by, 2, end fraction and labeled it Polygon D DD. What is the area of Polygon D DD?
Answers
Answer:
10 square units.
Step-by-step explanation:
Area of Polygon C = 40 square units.
Scale factor used in obtaining polygon D = \(\dfrac12\)
To obtain the area of the new polygon, we multiply the area of the polygon from which it was derived by the square of the scale factor.
Therefore:
Area of Polygon D
\(=40 \times (\frac12)^2\\\\=40 \times \frac14\\\\=10$ square units\)
The area of polygon D is 10 square units.
GIVING 50 points
FIND THE VALUE OF X
PLEASE HELP WITH WORK AND STEPS SHOW THANK YOU
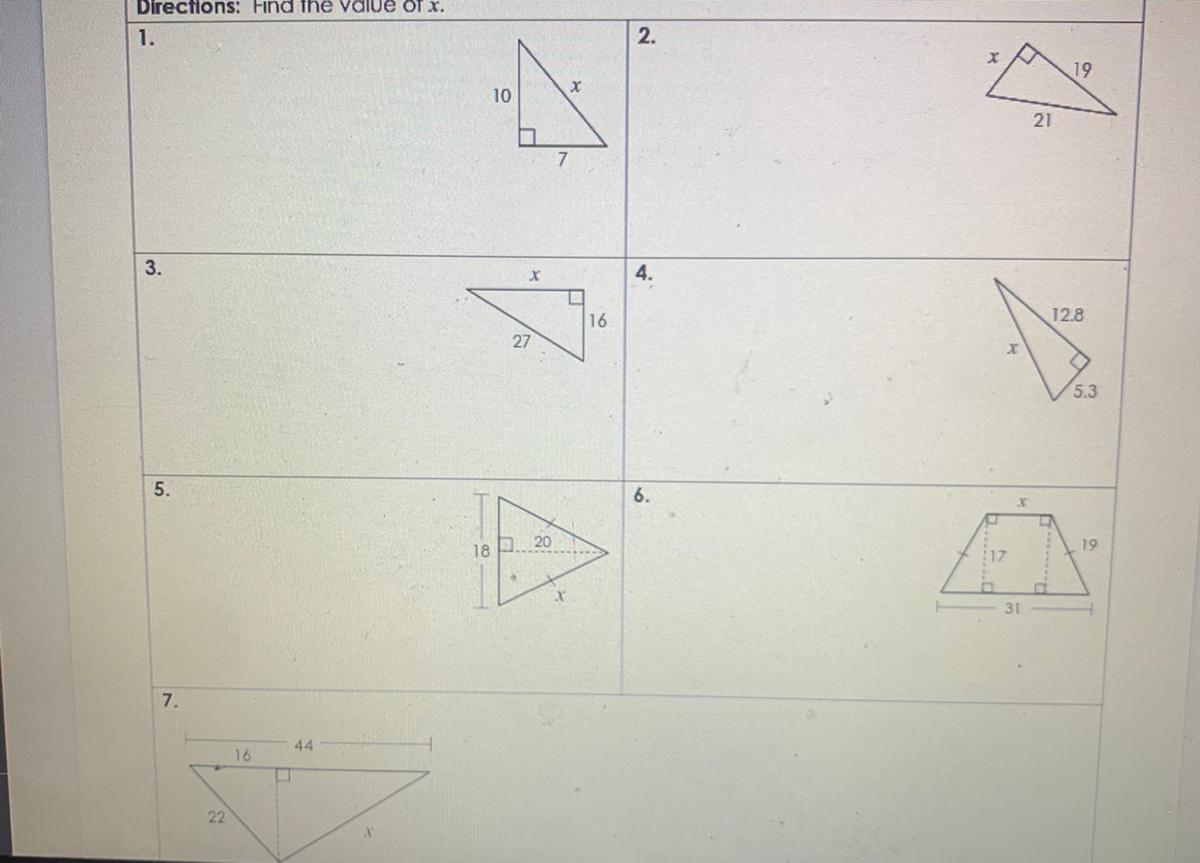
Answers
Answer:
Step-by-step explanation:
1. 10^2+7^2=x^2
x=sqrt(149)
2. 21^2-19^2=x^2
x=sqrt(80)
3. This is all pythagorean theorem busywork, a^2+b^2=c^2 where c is the hypotenuse of the triangle. I think from my examples you should be able to figure the rest out.
minimize f(x) = |x+3| + x^3 S.t. x sum [-2, 6]
Answers
Minimization of f(x) = |x+3| + x^3 at the endpoints (-2 and 6) the minimum value of the function is approximately 3.84, which occurs at x= \sqrt{1/3}
within the given interval.
To minimize the function subject to the constraint f(x) = |x+3| + x^3 that x lies in the interval [-2, 6], we need to find the value of x that minimizes f(x) within that interval.
First, let's analyze the function f(x). The absolute value term |x+3| can be rewritten as:
|x+3| =
x+3 if x+3 >= 0
-(x+3) if x+3 < 0
Since the interval [-2, 6] includes both positive and negative values of x+3, we need to consider both cases.
Case 1: x+3 >= 0
In this case, f(x) = (x+3) + x^3 = 2x + x^3 + 3
Case 2: x+3 < 0
In this case, f(x) = -(x+3) + x^3 = -2x + x^3 - 3
Now, we can find the minimum of f(x) within the given interval by evaluating the function at the endpoints (-2 and 6) and at any critical points within the interval.
Calculating the values of f(x) at x = -2, 6, and the critical points, we can determine the minimum value of f(x) and the corresponding value of x.
Since the equation involves both absolute value and a cubic term, it is not possible to find a closed-form solution or an exact minimum value without numerical methods or approximation techniques.
For more such questions on function
https://brainly.com/question/29631554
#SPJ8
Since from sentence 6 we know ¬C, we can apply modus ponens to sentence 7:
Answers
If sentence 6 states that ¬C is true, and sentence 7 presents a conditional statement with C as the antecedent and Q as the consequent, we can use modus ponens to infer that Q is false.
Modus ponens is a deductive reasoning rule that allows us to derive a conclusion from a conditional statement and its antecedent. Therefore, we can apply modus ponens to sentence 7 given that we know ¬C from sentence 6.
Since from sentence 6 we know ¬C, we can apply modus ponens to sentence 7. To do this, follow these steps:
1. Identify the premises: One premise is sentence 6, which states ¬C. The other premise should be a conditional statement, such as "If ¬C, then P" (replace P with the relevant proposition).
2. Apply modus ponens: Modus ponens is a rule of inference that allows us to deduce a conclusion from the given premises. If we have the premises "If ¬C, then P" and "¬C", we can conclude "P" using modus ponens.
3. State the conclusion: After applying modus ponens, we can conclude "P" based on the given premises, which include sentence 6 (¬C) and the conditional statement.
Visit here to learn more about antecedent:
brainly.com/question/28845527
#SPJ11
THIS IS A TEST NEED HELP!!
Each phrase in the table describes two variables which are strongly correlated. Select all phrases that imply correlation without causation.

Answers
they seem the most correct cos the first statements don’t cause the next ones
hope this helps
Just one please help

Answers
\(\displaystyle\\\\ Answer: A=\frac{2P}{xV^3}\)
Step-by-step explanation:
\(\displaystyle\\P=\frac{1}{2} xAV^3\\\)
Multiply both parts of the equation by 2:
\(2P=xAV^3\)
Divide both parts of the equation by xV³:
\(\displaystyle\\\frac{2P}{xV^3} =A\)
\(\displaystyle\\\\Thus,\ A=\frac{2P}{xV^3}\)
on a standardized exam, the scores are normally distributed with a mean of 140 and a standard deviation of 20. find the z-score of a person who scored 140 on the exam.
Answers
On a standardized exam, the scores are normally distributed with a mean of 140 and a standard deviation of 20. The z-score of a person who scored 140 on the exam is 0
The z-score of a person who scored 140 on an exam can be calculated using the formula z = (x - μ) / σ
where x is the exam score, μ is the mean of the exam scores, and σ is the standard deviation of the exam scores.
In this case, x = 140, μ = 140, and σ = 20.
Plugging these values into the formula, we get z = (140 - 140) / 20 = 0
Therefore, the z-score of a person who scored 140 on the exam is 0.
The z-score represents the number of standard deviations away from the mean that a particular value falls. A z-score of 0 indicates that the value is equal to the mean, which is 140 in this case. If a z-score is positive, it means that the value is above the mean, and if it is negative, it means that the value is below the mean. For example, a z-score of 1 indicates that the value is one standard deviation above the mean, and a z-score of -1 indicates that the value is one standard deviation below the mean.
Know more about Z-score here :
https://brainly.com/question/25638875
#SPJ11