A parabola opening up or down has vertex (0, 1) and passes through (12, -17). Write its
equation in vertex form.
Simplify any fractions.
Answers
The equation of the parabola is y = (-3/2)x + 1.
The general vertex form of the equation of a parabola is y = a(x - h)2 + k
where (h, k) are the coordinates of the vertex
Here, we are given that vertex = (0, 1)
Thus, the equation of the parabola is-
y = a(x - 0)2 + 1
y = 2ax + 1
Also, we are given that the parabola passes through (12, -17).
Thus, (12, -17) must satisfy the equation of the parabola
⇒ -17 = 2a(12) + 1
-17 = 24a + 1
24a = -17 -1
24a = -18
a = -18/24
a = -3/4
Thus, the equation of the parabola becomes-
y = 2(-3/4)x + 1
y = (-3/2)x + 1
Learn more about parabolas here-
https://brainly.com/question/17987697
#SPJ9
Related Questions
find all relative extrema of the function. use the second derivative test where applicable. (if an answer does not exist, enter dne.) y = x2 log2 x
Answers
The function y = x²log2(x) has a relative minimum at x = 1 and no other relative extrema.
To find the relative extrema of the function y = x²log2(x), we need to determine the critical points and apply the second derivative test where applicable. First, we find the derivative of the function using the product rule:
dy/dx = 2x log2(x) + x²* 1/x * ln(2)
= 2x log2(x) + x ln(2)
To find the critical points, we set the derivative equal to zero:
2x log2(x) + x ln(2) = 0
Simplifying the equation, we have:
x log2(x) + x ln(2) = 0
x(log2(x) + ln(2)) = 0
Since x cannot be equal to zero, we solve the equation log2(x) + ln(2) = 0:
log2(x) = -ln(2)
\(x = 2^{(-ln(2))\)
The critical point is \(x = 2^{(-ln(2))\), which is approximately 0.2413.
Next, we check the second derivative to determine the nature of the critical point. Taking the derivative of the first derivative, we get:
d²y/dx² = 2 log2(x) + 2 + ln(2)
Evaluating the second derivative at \(x = 2^{(-ln(2))\), we find:
d²y/dx²=
\(=2 log2(2^{(-ln(2))}) + 2 + ln(2) \\=-2 ln(2) + 2 + ln(2) \\=2 - ln(2)\)
Since the second derivative is positive (2 - ln(2) > 0), the critical point at \(x = 2^{(-ln(2))\) is a relative minimum.
In conclusion, the function \(y = x^2 log2(x)\) has a relative minimum at x = 1 and no other relative extrema.
Learn more about derivative here: https://brainly.com/question/29144258
#SPJ11
Line u has a slope of -3/4. Line v is parallel to line u. What is the slope of v
Answers
Answer:
-3/4
Step-by-step explanation:
Slopes are equal for parallel lines
Slope of line v is -3/4
What values of x and y satisfy the system {y=−2x+3y=5x−4?
Enter your answer as an ordered pair, like this: (42, 53)
If your answer includes one or more fractions, use the / symbol to separate numerators and denominators. For example, if your answer is (4253,6475), enter it like this: (42/53, 64/75)
If there is no solution, enter "no"; if there are infinitely many solutions, enter "inf."
Answers
The solution to the given system of equations is x = 1, y = 1. That is, (1, 1)
From the question, we are to solve the given system of equations.
The given system of equations is
y = -2x + 3y ------------- (1)
y = 5x - 4 ------------- (2)
Substitute equation (2) into equation (1)
y = -2x + 3y
5x - 4 = -2x + 3(5x - 4)
5x - 4 = -2x + 15x - `12
Collect like terms
-4 + 12 = -2x + 15x - 5x
Simplify
8 = 8x
∴ x = 8/8
x = 1
Substitute the value of x into equation (2)
y = 5x - 4
y = 5(1) - 4
y = 5 - 4
y = 1
Hence, the solution to the given system of equations is x = 1, y = 1. That is, (1, 1)
Learn more on Solving system of equations here: https://brainly.com/question/26310043
#SPJ1
need help with all of these questions you see on the top. there the red squares. please someone smart. this is one of the problems I need to finish this tonight.

Answers
Answer:
2412.7 ft^3
Step-by-step explanation:
If a circle has a diameter 16ft, it's radius is half that, or 8ft. The are of the circle/base of the cylinder is given by the formula \(\pi r^2\) where r is the radius. This means the area is 64π ft^2.
To find the volume of a cylinder, you multiply the base area and the height, so the volume would be 64π x 12 which is 2412.74315796. When rounded to the nearest tenth, this is 2412.7.
Since we want to find the volume of a cylinder:
⇒ must know the formula: \(V = \pi r^2h\)
r: radiush: heightConsider the information given:
Height: 12 ftDiameter: 16 ft ⇒ Radius: 8 ft (radius is half of the diameter)Let's solve:
\(V = \pi r^2*h=3.14*(8)^2*12=2411.52_.cm^3\)
Answer: 2411.5 cm³
Hope that helps!
What’s the domain and rangeee

Answers
Answer:
the domain is 2, and the range is 1
Step-by-step explanation:
A company buys machinery for $500000 and pays it off by 20 equal six-monthly instalments, the first payment being made six months after the loan is taken out. If the interest rate is 12%pa, compounded monthly, how much will each instalment be?
Answers
Each installment will be approximately $15,280.55.
To calculate the equal six-monthly installment, we can use the formula for the present value of an annuity.
Principal amount (P) = $500,000
Interest rate (r) = 12% per annum = 12/100 = 0.12 (compounded monthly)
Number of periods (n) = 20 (since there are 20 equal six-monthly installments)
The formula for the present value of an annuity is:
\(P = A * (1 - (1 + r)^(-n)) / r\)
Where:
P = Principal amount
A = Equal installment amount
r = Interest rate per period
n = Number of periods
Substituting the given values into the formula, we have:
$500,000 = \(A * (1 - (1 + 0.12/12)^(-20)) / (0.12/12)\)
Simplifying the equation:
$500,000 = A * (1 - (1.01)^(-20)) / (0.01)
$500,000 = A * (1 - 0.6726) / 0.01
$500,000 = A * 0.3274 / 0.01
$500,000 = A * 32.74
Dividing both sides by 32.74:
A = $500,000 / 32.74
A ≈ $15,280.55
Therefore, each installment will be approximately $15,280.55.
Learn more about Principal amount here:
https://brainly.com/question/30163719
#SPJ11
Solve for x. Enter the solutions from least to
greatest.
.
(x - 10)2 - 1 = 0
Answers
2x -21=0
2x=21
x= 10.5
Answer:
9 and 11
Step-by-step explanation:
khan :)
Question 4 A certain automotive dealer sells only cars and trucks, and the ratio of cars to trucks on the lotis 11 to 33. If there are currently 51 trucks for sale, how many cars does the dealer have for sale! a. 34 b. 68 c. 136 d. 272 thierronse
Answers
The number of cars that the dealer have for sale is 17 cars.
How many cars does the dealer have for sale?From the problem given, if the ratio of cars to trucks on the lot is 11 to 33, we can write this as: Cars/Trucks = 11/33
We can also simplify this ratio by dividing both sides by 11:
==> cars/51 = 11/33
Now we can solve for the number of cars:
Cars = (11/33) * 51
Cars = 17. Therefore, the dealer has 17 cars for sale.
Read more about Ratio
brainly.com/question/2328454
#SPJ1
helpppppppppppppppp i dont know this

Answers
Answer:
f(- 3) = - 16
Step-by-step explanation:
To evaluate f(- 3) with x = - 3 in the interval x ≤ - 2, then
f(- 3) = 5x - 1 = 5(- 3) - 1 = - 15 - 1 = - 16
let t be a linear transformation defined by a square matrix a. prove that t is an isomorphism if and only if a is nonsingular.
Answers
A linear transformation t defined by a square matrix a is an isomorphism if and only if a is nonsingular.
To prove this statement, we first recall that an isomorphism is a linear transformation that is both injective (one-to-one) and surjective (onto). If t is an isomorphism, then it is invertible, which means that there exists another linear transformation t^-1 such that t(t^-1(x)) = x and t^-1(t(x)) = x for all vectors x in the domain of t. In matrix notation, this means that aa^-1 = a^-1a = I, where I is the identity matrix.
Now suppose that a is nonsingular, which means that its determinant det(a) is nonzero. This implies that a^-1 exists and is also a square matrix. If we can show that t is injective and surjective, then we can conclude that t is an isomorphism. To prove injectivity, suppose that t(x) = t(y) for some vectors x and y. Then ax = ay, which implies that a(x - y) = 0. Since det(a) is nonzero, it follows that x - y = 0, which means that x = y. Thus, t is injective. To prove surjectivity, let z be an arbitrary vector in the range of t. Then there exists a vector y such that t(y) = z.
This implies that ay = z, which means that y = a^-1z. Thus, every vector in the range of t can be written as t(a^-1z), which shows that t is surjective. Therefore, we can conclude that t is an isomorphism if a is nonsingular. Conversely, if t is an isomorphism, then it must be invertible, which implies that a must be nonsingular, as we showed earlier. Thus, t is an isomorphism if and only if a is nonsingular.
Learn more about isomorphism here: brainly.com/question/32066433
#SPJ11
A baseball bat strikes a ball with an average force of 2.0 x 104 Newtons. if the bat stays in contact with the ball for a distance of 5.0 x 10-3 meter, what kinetic energy will the ball acquire from the bat?
1.0 x 102 J
2.0 x 102 J
2.5 x 101 J
4.0 x 102 J
Answers
The kinetic energy will the ball acquire from the bat is 2× 10² J
According to the question
Bat stays in contact for 5.0 X 10⁻³ and the ball travels at a speed of 2.0 X 10⁴.
An object's kinetic energy is the power it has as a result of motion. It is explained as the amount of effort required to move a mass-based body from rest to the indicated velocity.
The body keeps its kinetic energy, which it acquired during acceleration, unless its speed changes.
A mass m object moving at a speed v has kinetic energy 1/2 mv² according to classical mechanics.
Favg= -1/2 MV²
K= -1 2 ( 5.0 x 10⁻³)²
K = - 1/2 ×25 × 10⁻⁶
K = 2× 10² J
To know more about kinetic energy here
https://brainly.com/question/999862
#SPJ4
the diagram below shows three positions, a, b, and c, in the swing of a pendulum, released from rest at point a. [neglect friction.] which statement is true about this swinging pendulum?
Answers
Based on the information provided and considering the terms "pendulum" "positions a, b, and c," and "neglect friction," the true statement about the swinging pendulum is:
At position A, the pendulum has maximum potential energy and no kinetic energy. As it swings towards position B, its potential energy decreases while its kinetic energy increases. At position B, the pendulum has maximum kinetic energy and minimum potential energy. Then, as it moves towards position C, the kinetic energy decreases while the potential energy increases. At position C, it has the same potential energy as at position A, and the cycle repeats.
Potential energy is the energy possessed by an object due to its position or configuration relative to other objects. It is a form of stored energy that has the potential to be converted into other forms of energy and do work.
In the case of an object in a gravitational field, such as a pendulum, potential energy is associated with its vertical position above a reference point, often the ground. The higher the object is lifted, the greater its potential energy. The two most common forms of potential energy are gravitational potential energy and elastic potential energy.
To know more about gravitational potential energy, visit:
https://brainly.com/question/3910603
#SPJ11
he first step that Sarah performed to simplify the expression StartFraction 4(6.8 minus 4.2) plus 8.2 over 2 EndFraction before entering it into the calculator is shown.
2(3.4 – 2.1) + 4.1
Which statement is true?
Sarah performed the first step correctly.
The first step should have been 2(6.8 – 4.2) + 8.2.
The first step should have been StartFraction 27.2 minus 4.2 plus 8.2 over 2 EndFraction.
The first step should have been StartFraction 4(2.6) plus 8.2 over 2 EndFraction.
Answers
Sarah performed the first step correctly.
Given the function that Sarah performed as:
\(\dfrac{4(6.8-4.2)+8.2}{2}\)
To simplify the function, the first step Sarah carries out is to divide the numerator by 2:
\(\dfrac{4(6.8-4.2)+8.2}{2} \\= \frac{2(2)(2(3.4)-2(2.1)+2(4.1))}{2}\\=2(3.4 - 2.1) + 4.1\)
This shows that Sarah performed the first step correctly.
Learn more on decimal here: https://brainly.com/question/20123476
In the figure below, a ∥
∥
b, ∠
∠
1 = 9x - 4 and ∠
∠
2 = 13x - 32. What is ∠
∠
3
Answers
Applying the corresponding angles theorem, the measure of angle 3 is: C. 121°.
How to Apply the Corresponding Angles Theorem?Using the figure below that shows that line a is parallel to line b, where angle 1 and angle 2 are corresponding angles, based on the corresponding angles theorem, the measure of angle 1 is equal or congruent to angle 2.
Given the following:
Measure of angle 1 = 9x - 4
Measure of angle 2 = 13x - 32
m<1 = m<2 [corresponding angles theorem]
Substitute
9x - 4 = 13x - 32
Solve for the value of x
9x - 13x = 4 - 32
-4x = -28
x = 7
Measure of angle 3 = 180 - (13x - 32)
Plug in the value of x
Measure of angle 3 = 180 - (13(7) - 32)
m<3 = 121°
Learn more about the corresponding angles theorem on:
https://brainly.com/question/28182407
#SPJ1

Find the length of arc AB when the diameter of circle C is 10 inches.
20π in
2600π in
125π9 in
25π9 in

Answers
Answer:
Its the third one
Step-by-step explanation:
i did the test
Mr. Garcia's storage shed area has a length that is 7
feet more than twice the width. His storage shed is
a rectangular shape. The perimeter of the garden is
50 feet. Find the measurements of the Width and
Length
Answers
Answer:
width = 6 feet
length = 19 feet
Step-by-step explanation:
'w' = width
'2w+7' = length
50 = 2w + 2(2w+7)
50 = 2w + 4w + 14
36 = 6w
6 = w
length = 2(6)+7 = 19
a newsletter publisher believes that 333% of their readers own a rolls royce. a testing firm believes this is inaccurate and performs a test to dispute the publisher's claim. after performing a test at the 0.100.10 level of significance, the testing firm fails to reject the null hypothesis. what is the conclusion regarding the publisher's claim?
Answers
There is sufficient evidence at the 0.10 level of significance that the percentage is not 33%.
According to the newsletter publisher that 33% of their readers own a Rolls Royce.
The testing firm says that this is an inaccurate issue and performs a test to dispute the publisher's claim, after performing the test at the 0.10 level of significance the results are as follows,
Null hypothesis:
H₀ : p = 0.33
Alternative hypothesis:
H₁ : p ≠ 0.33
We reject H₀ at the 0.10 level of significance.
Therefore, There is sufficient evidence at the 0.10 level of significance that the percentage is not 33%.
To learn more about Hypothesis click here:
https://brainly.com/question/8409823
#SPJ4
Why Chebyshev's inequality produces approximate probability? Explain
Answers
Chebyshev's inequality produces an approximate probability because it provides an upper bound on the probability of deviation from the mean based on the standard deviation, without relying on specific distributional assumptions.
Chebyshev's inequality is a mathematical inequality that provides an upper bound on the probability that a random variable deviates from its mean by a certain amount. It states that for any random variable with a finite mean and variance, the probability that the random variable deviates from its mean by more than a certain number of standard deviations is bounded by a specific value.
The inequality is given by:
P(|X - μ| ≥ kσ) ≤ \(1/k^2\)
where X is the random variable, μ is its mean, σ is its standard deviation, and k is a positive constant.
Chebyshev's inequality is considered an approximate probability because it provides a conservative bound on the probability of deviation. It guarantees that the probability of a deviation beyond k standard deviations is no more than 1/k^2. However, it does not provide the exact probability of such deviations.
The approximation arises because Chebyshev's inequality applies to any distribution with a finite mean and variance, regardless of its specific shape. It does not rely on any assumptions about the underlying distribution, making it a very general result. However, this generality comes at the cost of accuracy. The inequality does not take into account the specific characteristics or shape of the distribution, so it may be a loose bound in some cases.
Learn more about statistics here:
https://brainly.com/question/15525560
#SPJ11
(Will give brainliest answer)
NEED HELP ASAP! SHOW SOLUTION AND EXPLANATION PLEASE!!
1. Find the volume of the solid that results when the region enclosed by the given curves = ^(−2), = 0, = 0, and = 1 is revolved about the x-axis.
2. Find the volume of the solid that results when the region enclosed by the given curves = ^(−2), = 0, = 0, and = 1 is revolved about the y-axis.

Answers
The volume of the solid that results when the region enclosed by the given curves y = e⁻²ˣ, y = 0, x = 0, and x = 1 is revolved around the x-axis and the y-axis is 0.77 and 0.7135.
What is the revolution of the curve?Revolving the region bordered by y = f(x) and the x-axis on the interval [a, b] around the x-axis generates the volume (V) of a solid.
The volume is given as
\(\rm Volume = \int _a^b \pi y^2 \ dx\)
The volume of the solid that results when the region enclosed by the given curves y = e⁻²ˣ, y = 0, x = 0, and x = 1 is revolved around the x-axis.
\(\rm Volume = \int _0^1 \pi (e^{-2x})^2 \ dx\\\\\\Volume = \int _0^1 \pi (e^{-4x}) dx\\\\\\Volume = \pi [\dfrac{e^{-4x}}{-4}]_0^1\\\\\\Volume = - \dfrac{\pi}{4} [e^{-4} - e^0]\\\\\\Volume = -\dfrac{\pi}{4} [-0.98168]\\\\\\Volume = 0.77\)
The volume of the solid that results when the region enclosed by the given curves y = e⁻²ˣ, y = 0, x = 0, and x = 1 is revolved around the y-axis.
\(\rm Volume = \pi \left [\int_{0}^{0.135} dy + \int_{0.135}^{1}\left ( \dfrac{\ln x}{-2} \right )^{2}dy \right ]\\\\Volume =0.71375\)
More about the revolution of the curve link is given below.
https://brainly.com/question/14640419
#SPJ1
math nation aaaaaaaaaaaaaaaaaaaaaaaaaaaaaa



Answers
Answer:
1. 80 2. 40
Step-by-step explanation:
because it's parallel to the other side
Please Answer! I have been working on this for an hour and can't get it!
Given A (4,2) and B (-1,y), what is y when the slope of AB is -7/5?
Answers
Answer: y= 9
Step-by-step explanation:
B = (- 1, y)
We know that the slope is -7/5 which is rise/run
Thankfully the run is 5 which is the exact distance from 4 to -1 so we would need to apply -7 to 2 which would be 5
The answer is
B = (- 1, 5)
Omar runs 6 miles in 55 minutes. At the same rate, how many miles would he run in 44 minutes?
In miles
Answers
Answer:
4.8 miles
Step-by-step explanation:
You can use a proportion.
6/55 = x/44
55x = 6 × 44
55x = 264
x = 264/55
x = 4.8
Answer: 4.8 miles
44 / 55 = 4 / 5
4 / 5 = 0.8
0.8 * 6 = 4.8 miles
please give brainliest
4 Find the area of the region determined by the following curves. In each case sketch the region. (a) y2 = x + 2 and y (b) y = cos x, y = ex and x = . (c) x = y2 – 4y, x = 2y – y2 + 4, y = 0 and y = 1. = X. TT 2 2 = = = = 2
Answers
The area of the region determined by the following curves is explained below.
The sketches of the region of each case are given at the end of each part.(a) y² = x + 2 and y.
This is the intersection of y = ± √(x+2) where x ≥ -2.
Sketching the curves, it is found that the region of intersection is the part of the parabola above the x-axis.
Sketch of region(b) y = cos x,
y = eⁿ and
x = π/2
The curves meet at y = cos x and
y = eⁿ.
Solving for x gives x = cos⁻¹(y) and
x = n.π/2, respectively.
For the intersection of these curves to exist, we need to solve eⁿ = cos x for x, which has many solutions.
One solution is x ≈ 1.378.
Since e is a larger function than cos, the graph of y = eⁿ will be higher than the graph of
y = cos x on this interval.
Thus the region determined by these curves will be part of the graph of y = eⁿ that lies between
x = 0 and x ≈ 1.378.
Since the lines x = 0 and x = π/2 bound the area, we take the integral of eⁿ from 0 to approximately 1.378, giving an area of approximately 2.891.
Sketch of region(c) x = y² - 4y,
x = 2y - y² + 4,
y = 0 and
y = 1.
To find the area of the region, we first solve the two equations for x.
We get x = y² - 4y and
x = 2y - y² + 4.
To find the bounds of integration, we look at the y-values of the intersection points of the curves.
At the points of intersection, we have y² - 4y = 2y - y² + 4.
This simplifies to y⁴ - 6y³ + 16y² - 16y + 4 = 0,
which can be factored as (y-1)²(y² - 4y + 4) = 0.
Thus y = 1 or
y = 2 (twice).
Since we are given that y = 0 and
y = 1 bound the region, we integrate over [0, 1].
Therefore, the area of the region is ∫₀¹[(y² - 4y) - (2y - y² + 4)]dy.
Expanding and integrating gives an area of 13/6.
Sketch of region.
To learn more about parabola, visit:
https://brainly.com/question/31142122
#SPJ11
Find the area of the the regular polygon.

Answers
Answer:
Area of Regular Polygon = ( About ) 332.6 units^2; Option C
Step-by-step explanation:
~ Let us first declare consecutive notes. If we were to draw an altitude in this triangle, it would be perpendicular to the base, by definition. At the same time this shape is a regular polygon, so all sides ( and angles ) are ≅. This would mean that, by Coincidence Theorem, the altitude divides the base into the two ≅ parts. ~
1. If that is so, the altitude would split this base into parts ⇒ ( 16√3 )/2 = 8√3.
2. This would mean that the altitude can be found through Pythagorean Theorem, provided that by definition it forms a 90 degree angle at the base. Let us say x ⇒ the length of the altitude, ( 8√3 )^2 + ( x )^2 = ( 16√3 )^2 ⇒ 192 + x^2 = 768 ⇒ x^2 = 576 ⇒ length of altitude - 24 units
3. With the base 16√3 units, and the the altitude/height 24 units, we can find the area of this regular polygon to be ⇒ 1/2 * base * height ⇒ 1/2 * 16√3 * 24 ⇒ 192√3 units^2
4. That being said that area would be 192 * 1.732050808...... ⇒
Area of Regular Polygon = ( About ) 332.6 units^2
Express the function graphed
on the axes below as a piecewise function.

Answers
The required piece-wise function shown in the graph is y = x + 1 for x < 2 and y = 2x - 1 for x > 2.
To determine the equation of the given piece-wise function,
The equation of the function under x < 2 is given as,
y = x + 1 for x < 2
This equation can be obtained by locating two points on the line such as (-1, 0) and (0, 1), and forming an equation with these points,
Similarly,
For x > 2, we have
y = 2x - 1
Thus, the required piece-wise function shown in the graph is y = x + 1 for x < 2 and y = 2x - 1 for x > 2.
Learn more about piece-wise function here:
https://brainly.com/question/22051192
#SPJ1
Patty needs a total of $80 to buy a bicycle. She has already saved $35. If she saves $10 a week from her earnings, what is the least number of weeks she must work to have enough money to buy the bicycle?
Answers
Answer:
5 weeks
Step-by-step explanation:
She would need to work at least 8 weeks because the bicycle is $80 and she has $35.
Answer:
5 weeks
Step-by-step explanation:
i took 80 - 35 to get 45 (money she still needs)
then took 45 divided by 10 to get 4.5 ( how many weeks till she has the money)
and if you get 10 dollars per week and its asking how many weeks
you have to up the 4 by one because it has a .5
so it would be 5 weeks
Find the measure of the missing angle of the triangle.
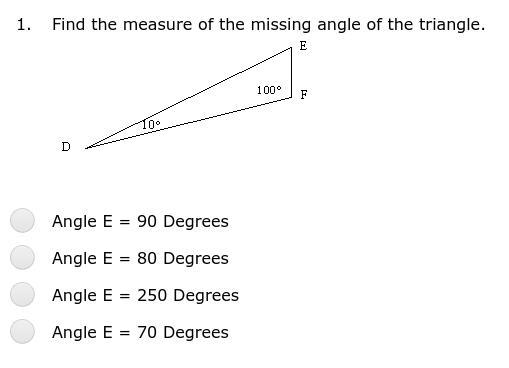
Answers
Answer:
The interior angles of a triangle add up to 180 degrees, so Angle E = 70 degrees.
in how many ways can you create a two-element set where each element in the set is an positive integer less than 95?
Answers
In order to establish a two-element set with each element being a positive integer smaller than 95, there are thus 4371 possible combinations.
Combinations are defined by the following formula: C(n, r) = n! / (r! * (n-r)!)
Where n is the overall number of things and r denotes the number of items to be picked at random.
Without respect to order, we must select 2 elements from a possible total of 94. As a result, we can use the following formula to apply the rule: C(94, 2) = 94! / (2! * (94-2)!) = (94 * 93 * 92 *... * 3 * 2 * 1) / [(2 * 1) * (92 * 91 *... * 3 * 2 * 1)]
= (94 * 93) / (2 * 1) = 4371
To know more about combination,
https://brainly.com/question/25653387
#SPJ11
what value of p makes the expression true? -3p+1/8=-1/4
Answers
Answer:
p = 1/8
Step-by-step explanation:
Step 1: Write out equation
-3p + 1/8 = -1/4
Step 2: Subtract 1/8 on both sides
-3p = -3/8
Step 3: Divide both sides by -3
p = 1/8
PLSSS HELP ANSWER THESE QUESTIONS! WORTH 35 POINTS WILL GIVE BRIANLIEST IF ANWRS ARE CORRECT!
For which value of x do following expressions make sense?
THE FOLLOWING QUESTION HAVE TO BE ANWERED AS X IS LE THAN OR GREATER THAN WHATEVER THE ANWER IS
43a) √x+5 40a) ∛a 44b) √(-5x)^3 47e) √13-(13-2x)
THE NEXT COUPLE OF QUETION HAVE TO ANWERED AS X = WHATEVER THE ANSWER IS.
43b) √|x| + 1 44a) √(-2x)^2
45a) √x-5 = 3 The root is only over x-5
45b) √2x+4 = 2 the root is only over 2x+ 4
45c) √x(x+1) = 0 root is only over x(x+1)
45d) √x+5 = -1 the root is only over x+5
45e) √x + x^2 = 0 the root is only over x
42d) root 5 over x+3 = 17 1
9e) root 4 over x = 1 THE ANSWER IS NOT 1
19f) ∛x - 2 = 0 the root is only over x
THE FOLLOWING QUESTIONS HAVE NUMERICAL ANSWERS
9a) root 0.6 over 36 9h) root (4-10) over 0.01
Answers
The values of the variables and numbers in radical form are presented as follows;
43a) x > -5
40a) a > 0
44b) x < 0
47e) x > 0
43b) x = The set of all real numbers
44a) The set of all numbers
45 a) x = 14
45 b) x = 0
45 c) x = -1
45 d) x = -4
45 e) x = 1
42 d)x = 5/196
9 e) x = 4
9 f) x = 8
9 a) √(0.6/36) ≈ 0.13
9 h) √((4 - 10)/(0.01)) = i·10·√6
What is a radical expression in mathematics?A radical also known as a root is represented using the square root or nth root symbol and is the opposite of an exponent.
43 a) \(\sqrt{x + 5}\)
x + 5 > 0
Therefore, x > -5
40a) ∛a
a > 0
44b) √(-5·x)³
-5·x < 0
x < 0
47e) √(13 - (13 - 2·x))
(13 - (13 - 2·x)) > 0
13 > (13 - 2·x)
0 > -2·x
x > 0
43b) √|x| + 1
x = All real numbers
44 a) √(-2·x)²
√(-2·x)² = -2·x
x = Set of all numbers
45 a) √(x - 5) = 3
(x - 5) = 3² = 9
x = 9 + 5 = 14
45b) √(2·x + 4) = 2
2·x + 4 = 2²
2·x = 2² - 4 = 0
x = 0/2 = 0
45c) √(x·(x + 1)) = 0
(x·(x + 1)) = 0
(x + 1) = 0
x = -1
45 d) √(x + 5) = -1
(x + 5) = (-1)²
x + 5 = 1
x + 5 = 1
x = 1 - 5 = -4
x = -4
45e) √x + x² = 0
√x = -x²
(√x)² = (-x²)² = x⁴
x = x⁴
1 = x⁴ ÷ x = x³
x = ∛1 = 1
x = 1
42d) \(\sqrt{\dfrac{5}{x} } +3= 17\)
\(\sqrt{\dfrac{5}{x} }= 17-3 =14\)
\(\dfrac{5}{x} }=14^2=196\)
\(x = \dfrac{5}{196}\)
9e) \(\sqrt{\dfrac{4}{x} } = 1\)
\(\dfrac{4}{x} } = 1^2\)
x × 1² = 4
x = 4
19f) ∛x - 2 = 0
∛x = 2
x = 2³ = 8
9a) \(\sqrt{\dfrac{0.6}{36} }\)
\(\sqrt{\dfrac{0.6}{36} }\) = \(\sqrt{\dfrac{1}{60} }= \dfrac{\sqrt{15}}{30} \approx 0.13\)
9h) \(\sqrt{\dfrac{4-10}{0.01} }\)
\(\sqrt{\dfrac{4-10}{0.01} }\)= √(-600) = √(-1)·√(600) = i·10·√6
Learn more about the square root of numbers here:
https://brainly.com/question/428672
#SPJ1