A number is chosen at random from 1 to 25. Find the probability of selecting a number greater than 19.
Answers
The probability of selecting a number greater than 19 from 1 to 25 is 6/25 or 0.24.
What is Probability:
The probabilities of an event occurring are defined by probability.
The ratio of favorable outcomes to all possible outcomes of an event is known as probability.
The formula for the Probability of an event is given by
Probability(Event) = Favorable Outcomes/Total Outcomes
Here we have
The set of numbers is from 1 to 25
Total number of numbers from 1 to 25 = 25
In given set of numbers, the number which is greater than 19 are
=> 20, 21, 22, 23, 24, and 25.
The number of favorable outcomes (getting a number, > 19 ) = 6
From the above information,
Probability of selecting a number greater than 19 = 6/25 = 0.24
Therefore,
The probability of selecting a number greater than 19 from 1 to 25 is 6/25 or 0.24
Learn more about Probability at
https://brainly.com/question/11234923
#SPJ1
Related Questions
A farmer wants to fence an area of 5400 square feet in a rectangular field and then divide it in half with a fence parallel to one of the sides of the rectangle. What should the lengths of the sides of the rectangular field be so as to minimize the amount of fencing needed?.
Answers
90 feet is the lengths of the sides of the rectangular field .
What do you mean by rectangular?
A rectangle is a sort of quadrilateral with parallel sides that are equal to one another and four vertices that are all 90 degrees apart.Because of this, it is also known as an equiangular quadrilateral. Because the opposite sides of a rectangle are equal and parallel, it can also be referred to as a parallelogram.Let x represent the length of the fence and y represent the width of the fence.
Since the area is 5400, hence:
Area = length * width = x * y
5400 = xy
y = 5400/x
A fence divide the field in half and is parallel to one of the sides of the rectangle. Hence:
Amount of fencing needed (P) = x + x + y + y + y = 2x + 3y
Amount of fencing needed (P) = 2x + 3(5400/x) = 2x + 16200/xTo minimize
the amount of fencing needed, dP/dx = 0, hence:
dP/dx = 2 - 16200/x²
2 - 16200/x² = 0
2 = 16200/x²
2x² = 16200
x² = 8100
x = 90 feet
y = 5400/x = 5400/90 = 90 feet
Learn more about rectangular
brainly.com/question/15019502
#SPJ4
Math practice for math tmr
Graph:

Answers
Answer:
its 1/2
Step-by-step explanation:
Answer:
math
Step-by-step explanation:
An eating disorder characterized by bingeing and purging is called The minimum amount of body fat needed for good health is Youris the amount of energy your body uses at complete rest. A term used to describe a person who is very overfat is People with extremely thin. see themselves as too fat even when they are A technique for assessing body fat levels that involves being weighed under water is called
Answers
An eating disorder characterized by bingeing and purging is called bulimia nervosa.
The minimum amount of body fat needed for good health is variable and can depend on factors such as age, gender, and individual circumstances. However, essential body fat is typically estimated to be around 3-5% for men and 8-12% for women.
The term used to describe a person who is very overfat is obese. Obesity refers to having excessive body fat, which can have negative effects on health.
People with anorexia nervosa, an eating disorder characterized by restrictive eating and an intense fear of gaining weight, often see themselves as too fat even when they are extremely thin. This distorted body image is a characteristic feature of anorexia nervosa.
A technique for assessing body fat levels that involves being weighed under water is called hydrostatic weighing or underwater weighing. It is considered one of the more accurate methods for determining body composition.
To know more about bulimia nervosa., refer here:
https://brainly.com/question/32013975#
#SPJ11
Consider the wave packet: ψ(x)=[ 2πa 2
1
] 1/2
exp[− 4a 2
(x−⟨x⟩) 2
+i ℏ
px
]. Calculate the uncertainties ⟨Δx 2
⟩=⟨( x
^
−⟨x⟩) 2
⟩ and ⟨Δp 2
⟩=⟨( p
^
−⟨p⟩) 2
⟩, where ⟨ A
^
⟩ denotes the expectation value ⟨ψ∣ A
^
∣ψ⟩ of the observable A
^
on the state ∣ψ>.
Answers
The uncertainties ⟨Δx^2⟩ and ⟨Δp^2⟩ are given by the expressions ⟨Δx^2⟩ = a^2/2 and ⟨Δp^2⟩ = (ℏ^2)/(8a^2).
To calculate the uncertainties ⟨Δx^2⟩ and ⟨Δp^2⟩ for the given wave packet, we need to find the expectation values of the observables (x^ - ⟨x⟩)^2 and (p^ - ⟨p⟩)^2, respectively.
The wave packet is represented by the function ψ(x) = [2πa^2]^(1/2) exp[-4a^2(x - ⟨x⟩)^2 + iℏpx]. Here, a is a constant, ⟨x⟩ represents the expectation value of x, and p is the momentum operator.
To find ⟨Δx^2⟩, we calculate the expectation value of (x^ - ⟨x⟩)^2 with respect to ψ(x). By integrating (x - ⟨x⟩)^2 multiplied by the squared magnitude of the wave packet over all x values, we obtain the result ⟨Δx^2⟩ = a^2/2.
Similarly, to find ⟨Δp^2⟩, we calculate the expectation value of (p^ - ⟨p⟩)^2 with respect to ψ(x). Since p is the momentum operator, its expectation value is ⟨p⟩ = 0 for the given wave packet. By integrating (p^ - 0)^2 multiplied by the squared magnitude of the wave packet over all x values, we obtain the result ⟨Δp^2⟩ = (ℏ^2)/(8a^2).
Therefore, the uncertainties ⟨Δx^2⟩ and ⟨Δp^2⟩ are given by the expressions ⟨Δx^2⟩ = a^2/2 and ⟨Δp^2⟩ = (ℏ^2)/(8a^2).
Learn more about Expressions
brainly.com/question/28170201
#SPJ11
Can someone help me with this I don't get it

Answers
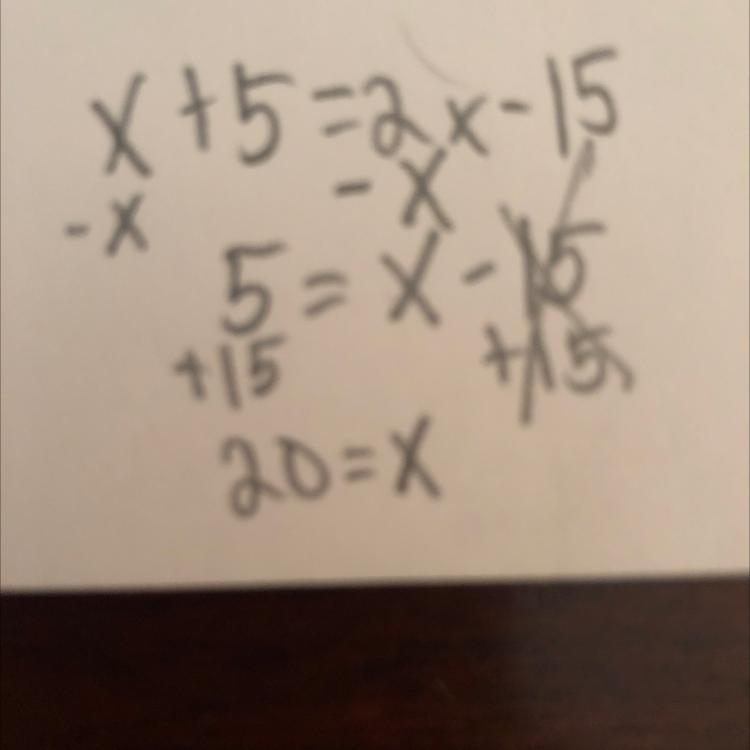
Gonzalez Manufacturing borrowed $21000. Part of the money was borrowed at 10%, part at 12%, and part at 14%. The total amount borrowed at 10% and 12%
was twice the amount borrowed at 14%. Find the amount borrowed at each rate if the annual interest was $2580
How much money was borrowed at 10%?
How much money was borrowed at 12%?
How much money was borrowed at 14%?
Answers
Answer:
10% — $550012% — $700014% — $8500Step-by-step explanation:
You want to know the amount borrowed at 10%, 12%, and 14% if the total borrowed was $21000, the total interest was $2580, and the total of amounts borrowed at 10% and 14% was double the amount borrowed at 12%.
EquationsThe relations give rise to three equations. If we let x, y, z represent the respective amounts borrowed at 10%, 12%, and 14%, we have ...
x + y + z = 21000 . . . . . . total borrowed
0.10x +0.12y +0.14z = 2580 . . . . . . total interest
x + y = 2z . . . . . . . . . . . relationship between amounts
Writing the last equation as ...
x -2y +z = 0
we can formulate the problem as a matrix equation and use a solver to find the solution. We have done that in the attachment. It tells us the amounts borrowed are ...
10% — $550012% — $700014% — $8500__
Additional comment
Recognizing that the amount at 12% is 1/3 of the total, we can use that fact to rewrite the other two equations. The interest on the $7000 at 12% is $840, so we have ...
x + y = 140000.10x +0.14y = 1740These two equations have the solution shown above. (It is usually convenient to solve them by substituting for x in the second equation.)
<95141404393>

The concept that relates how much one variable changes as another variable changes is?
Answers
The concept that relates how much one variable changes as another variable changes is Slope.
Slope is a numerical representation of how inclined a line is with respect to the horizontal. The ratio of the vertical to the horizontal distance between any two points on a line, ray, or line segment is known as its slope in analytic geometry ("slope equals rise over run").
The ratio of the increase in elevation between two points to the run in elevation between those same two points is referred to as the slope. The slope expresses how quickly the dependent variable changes when the independent variable changes. The Greek capital letter D or D is frequently used by mathematicians and economics to represent change. Slope contrasts changes in y or the vertical axis with changes in x or the horizontal axis.
Learn more about Slope here
https://brainly.com/question/3493733
#SPJ4
câu nào không phải mệnh đề
A. 3+2=7
B. 4+x
Answers
Answer:
b because it is an expressio n
Step-by-step explanation:
Choose
1. Identify the slope of the line with the given equation. y= 1/2X + -2
A) x
B) y
C) 1/2
D) -2
Answers
m is slope
Y = 1/2x + -2, the slope is 1/2
It would be C) 1/2
The baker made a batch of chocolate chip, oatmeal raisin, and sugar cookies. If P(chocolate chip) = 68%, interpret the likelihood of randomly selecting a chocolate chip cookie from the batch.
Likely
Unlikely
Equally likely and unlikely
This value is not possible to represent probability of a chance event.
Answers
Answer:
Likely
Step-by-step explanation:
68% is more than 2/3, so the event is likely to occur.
Answer: Likely
pls help me this is due now 30 points for it!

Answers

\(I need help can someone help? I’m really stuck and it’s so really soon! I need to show my work\)
![[tex]I need help can someone help? Im really stuck and its so really soon! I need to show my work[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/i3BkSJCapHMZSpnQnVU2edsFDfZpnW86.jpeg)
![[tex]I need help can someone help? Im really stuck and its so really soon! I need to show my work[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/bqM8fZvLqvWn1cv5NstyVmNlc8W0SVCj.jpeg)
Answers
S and t are binary relations on the set {a, b, c, d} and are defined as follows: s = { (a, b), (a, c), (b, d), (d, c) } t = { (b, b), (c, a), (c, d), (a, d) } select the set corresponding to t ∘ s
Answers
A set is a mathematical model for a collection of items. The correct option is C.
What is a set?A set is a mathematical model for a collection of items; it comprises elements or members, which may be any mathematical object: numbers, symbols, points in space, lines, other geometrical structures, variables, or even other sets.
Given the s={(a, b), (a, c), (b, d), (d, c)} and t={(b, b), (c, a), (c, d), (a, d)} Therefore, the value of t ∘ s = { (a, c), (b, d), (c, b), (c, c) }.
Hence, the correct option is C.
Learn more about Set:
https://brainly.com/question/8053622
#SPJ4

exercise 5.3.3. let h be a differentiable function defined on the interval [0, 3], and assume that h(0)
Answers
A differentiable function h(x) with specific conditions will have points where h(d) = d, h'(c) = 1/3, and h'(x) = 1/4.
(a) By the Intermediate Value Theorem, as h(x) is continuous, there exists a point d in the interval (0,3) where h(d) equals d, since h(0) = 1 and h(3) = 2.
(b) Using the Mean Value Theorem, as h(x) is differentiable, there exists a point c in (0,3) where h'(c) equals the average rate of change between h(0) and h(3), which is 1/3.
(c) By applying Rolle's theorem repeatedly, we can show that there exists a point in the domain of h(x) where the nth derivative of h(x) is zero.
Consequently, at that point, h'(x) is constant, and since h'(0) = h'(3), we can conclude that h'(x) equals 1/4 at some point in the domain.
Learn more about Function click here :brainly.com/question/572693
#SPJ11
Question - Exercise 5.3.3. Let h be a differentiable function defined on the interval (0,3), and assume that h(0) = 1, h(1) = 2, and h(3) = 2. (a) Argue that there exists a point de [0,3] where h(d) = d. (b) Argue that at some point c we have h'(c) = 1/3. (c) Argue that h'(x) = 1/4 at some point in the domain.
Can someone please help?

Answers
Answer:
(B) 26°
Step-by-step explanation:
The angle at A made by the radius and the tangent is 90°. The angle at O is the same as arc AB, 64°. The acute angles in a right triangle are complementary, so the angle at C is the complement of 64°.
∠ACB = 90° -64°
∠ACB = 26°
What is the solution of 6 = x-2/4?

Answers
Answer: x=13/2
Step-by-step explanation: hope this helps!
Select the correct answer from the drop-down menu. Find the polynomial. {5} is the solution set of.
Answers
Polynomials are expressions. The polynomial whose solution set is {5} is x²-10x+25.
What are polynomial?Polynomial is an expression that consists of indeterminates(variable) and coefficient, it involves mathematical operations such as addition, subtraction, multiplication, etc, and non-negative integer exponentials.
As it is given that the {5} is the solution set of the function, therefore, we can write,
\(x = 5\\(x-5 )= 0\)
Thus, (x-5) is one of the factors of the polynomial.
Let's assume that the 5 is the only root of the polynomial, therefore, if we multiply the factor by itself we will get the quadratic equation whose solution is only 5.
\((x-5)^2\\\\\text{Using the algebric identity we will get}\\\\x^2-10x+25\)
Hence, the polynomial whose solution set is {5} is x²-10x+25.
Learn more about Polynomials:
https://brainly.com/question/17822016
Answer:
x²-10x+25
Step-by-step explanation:
It was correct for me
A birds eggs are hatching there are 42 yellow baby birds and 41 red baby bird what is thr ratio of yellow birds to red birda
Answers
Answer:
42:41
Step-by-step explanation:
A spiral staircase turns as it rises 10 feet. The radius of the staircase is 3 feet. What is the number of feet in the length of the handrail
Answers
The number of feet in the length of the handrail is 17.3 feet.
What is a Pythagorean Theorem?Pythagorean theorem, is a geometric theorem that the total of a squares on the sides of a right triangle equals the square upon that hypotenuse (a side opposite its right angle)—or, using familiar algebraic notation, the sum of squared on the hypotenuse equals the square also on hypotenuse.
H² = B² + P²
A spiral would be a shape that wraps around and around with each curve being higher or lower than the one before it.
Now, according to the question;
The simplest way to understand this is to assume that we may "unfold" this spiral to form a rectangle.
Its bottom part of rectangle is simply an arc length of a 3 ft radius circle spun around 270°= (3/4) of a full revolution.
Thus,
= (3/4)× (2\(\pi\)) ×(3)
= (9/2)×\(\pi\) ft
= 4.5×\(\pi\) ft
The height of the staircase will be the side of rectangle = 10ft.
And the rectangle's diagonal will correspond to the length of a railing.
To solve this, we can apply the Pythagorean Theorem.
Handrail length = √ [ (4.5 ×\(\pi\))² + 10² ]
Handrail length ≈ 17.3 ft
Therefore, the the number of feet in the length of the handrail is 17.3 feet.
To know more about Pythagorean Theorem, here
https://brainly.com/question/343682
#SPJ4
The complete question is-
A spiral staircase turns 270° as it rises 10 feet. The radius of the staircase is 3 feet. What is the number of feet in the length of the handrail?
Each individual number in a sequence of numbers is called what?
Hint: book in your notes.
Term
Common difference
Geometric term
Successive term
Answers
Term
Step-by-step explanation:
hope so the answer is satisfying
You think there may be an issue with multicollinearity in your model. You calculate the VIF, for which you find a value of 13.55. Is this high or low, and what conclusion can you make from it
Answers
The issue with multicollinearity in the model should be investigated further because it can lead to unreliable regression coefficients, standard errors, and p-values.
The Variance Inflation Factor (VIF) is an excellent method to determine if multicollinearity exists in a model. Multicollinearity happens when the independent variables in the model are highly correlated with one another. This is a problem because it makes it tough to discern the individual impact of each independent variable on the dependent variable.High VIF values signal that multicollinearity may be a problem in the model. According to the rule of thumb, VIFs of 10 or greater are a sign of extreme multicollinearity.
As a result, a VIF of 13.55 is high. It implies that the independent variables are too strongly correlated and could be influencing one another's impacts on the dependent variable.
To know more about p-values visit:-
https://brainly.com/question/30182084
#SPJ11
AACB = ADCE
<A=50°, <C=45°, and <D=10x
x=[?]
Answers
Answer:
X=5
Step-by-step explanation:
Angle A is congruent to angle D.
Please help me im not sure how to do this problem.

Answers
Answer:
Step-by-step explanation:
Interior Angle to a Circle Theorem.
X° = 1/2 (130° + 142°)
x° = 1/2 (272°)
x° = 136°
bra9inly pls help me on this question

Answers
Step-by-step explanation:
area of the trapezoid = area of the 2 triangles +
area of the rectangle
i) area of triangle on left:
a = ½ bh
a = ½ × 2 × 9
a = 9 in²
ii) area of triangle on right:
a = ½ bh
a = ½ × 2 × 9
a = 9 in²
iii) area of rectangle = length × width
a = l × w
a = 12 × 9
a = 108 in²
iv) area of trapezoid = 9 + 9 + 108
= 126 in²
hope this helps you!
-s.
Which model represents a fraction greater than 3/5?

Answers
Answer:
the 2nd one
Step-by-step explanation:
Answer:
its the blue circle
Step-by-step explanation:
There is a bag with only red marbles and blue marbles. The probability of randomly choosing a red marble is 2 9 . There are 63 marbles in total in the bag and each is equally likely to be chosen. Work out how many red marbles there must be.
Answers
The main idea is the number of marbles and the denominator of the probability. All you have to do is multiply the fraction by a fraction which is equal to 1 which makes the denominator equal to 63. We know 63 is a multiple of 9. 9 goes 7 times in 63 so we multiple the fraction \(\frac{2}{9}\) with \(\frac{7}{7}\) which gives, \(\frac{2 * 7}{9 * 7}\) which when evaluated gives \(\frac{14}{63}\) and the numerator is the number of red marbles in the bag. So there are 14 red marbles in the bag :D
The weights of bags of baby carrots are normally distributed, with a mean of 28 ounces anda standard deviation of 0.34 ounce. Bags in the upper 4.5% are too heavy and must berepackaged. What is the most a bag of baby carrots can weigh and not need to berepackaged?
Answers
In order to find the maximum weight, first we need to find the value of z that corresponds to the upper 4.5%.
To do so, let's find the value of z with a score of:
\(score=100\%-4.5\%=1-0.045=0.955\)Looking at the z-table, the value of z for a score of 0.955 is equal to 1.695.
Now, to find the maximum weight x, we can use the formula below:
\(z=\frac{x-\mu}{\sigma}\)Where μ is the mean and σ is the standard deviation.
So, using the given values, we have:
\(\begin{gathered} 1.695=\frac{x-28}{0.34} \\ x-28=1.695\cdot0.34 \\ x-28=0.5763 \\ x=28.5763 \end{gathered}\)Rounding to two decimal places, we have a weight of 28.58 ounces.
Pls answer this, I really need help-


Answers
Answer: B
Step-by-step explanation:
Points from the graph
Points from f(x) points from g(x)
(1,2) (1, 1/2)
(4, 16) (4, 4)
f(x) was multiplied by 1/4 to get to g(x)
What is the value of X?

Answers
Answer:
I think the answer for this question is 2.24cm
Give the general solution of xy'+3y= ((4e^(-3x))) / (x^2)
Answers
The general solution of the given differential equation \($y = \left(-\frac{4\ln|x|}{x^3}\right)e^{-3x} + \frac{C}{x^3}$\), where C is an arbitrary constant.
The given differential equation is a first-order linear ordinary differential equation of the form \($xy' + 3y = f(x)$\) where \($f(x) = \frac{4e^{-3x}}{x^2}$\) .To solve this equation, we need to find an integrating factor, which is a function that when multiplied with the original equation, makes the left-hand side a derivative of a product of functions. To find the integrating factor, we multiply the equation by a function u(x), such that \($u(x)xy' + 3u(x)y = u(x)f(x)$\), and seek a function u(x) that makes the left-hand side a derivative of a product.
By comparing this equation with the product rule, we can see that the integrating factor is\($u(x) = e^{3\ln{|x|}}$\), which simplifies to \($u(x) = x^3$\).
Multiplying the original equation by the integrating factor, we get \($x^3y' + 3x^2y = \frac{4e^{-3x}}{x}$\). The left-hand side is now a derivative of the product \($(x^3y)$\), so we can integrate both sides with respect to x to obtain the general solution: \($x^3y = -4e^{-3x}\ln{|x|} + C$\) where C is the constant of integration.
Dividing both sides by \($x^3$\), we get the final form of the general solution. Therefore, the general solution of the given differential equation is \($y = \left(-\frac{4\ln{|x|}}{x^3}\right)e^{-3x} + \frac{C}{x^3}$\), where C is an arbitrary constant. This solution satisfies the original differential equation for all x except x = 0, where the solution is not defined due to the singularity in the coefficient.
Learn more about arbitrary constant here:
https://brainly.com/question/30466124
#SPJ11