A local talent is selling underground CD’s to get his rap career off the ground.
Each crate contains 60 blank CD’s.
Each crate cost $35.
How much should he sell his CD’s to make a profit of $85?
Answers
Answer:
He should sell his CD's for $2.
Step-by-step explanation:
Each crate contains 60 blank CD’s and each crate cost $35.
This means that he will pay $35 for 60 CD's.
How much should he sell his CD’s to make a profit of $85?
He will sell each of the 60 CD's for x, which means that his earnings will be of 60x.
Profit: Earnings - Cost = 60x - 35
To make a profit of $85
\(60x - 35 = 85\)
\(60x = 120\)
\(x = \frac{120}{60}\)
\(x = 2\)
He should sell his CD's for $2.
Related Questions
What is the solution (in interval notation) to the following inequality below? 3 x > 105 O (35,00) 0 (35,00) [35,00] O (-0,35)
Answers
We have the inequality
\(3x>105\)To solve we notice that the 3 multiplying x is positive, so we can divide both sides of the inequality by 3 without changing the sign. Then
\(\begin{gathered} 3x>105 \\ \frac{3x}{3}>\frac{105}{3} \\ x>35 \end{gathered}\)In interval notation this is
\((35,\infty)\)using the line of best fit

Answers
The monthly cell phone bill when shared data equals zero is given as follows:
$26.
How to define a linear function?The slope-intercept representation of a linear function is given by the equation presented as follows:
y = mx + b
The coefficients of the function and their meaning are described as follows:
m is the slope of the function, representing the change in the output variable y when the input variable x is increased by one.b is the y-intercept of the function, which is the initial value of the function, i.e., the numeric value of the function when the input variable x assumes a value of 0. On a graph, it is the value of y when the graph of the function crosses the y-axis.The intercept of the line in this problem is given as follows:
b = 26.
Hence $26 is the monthly cell phone bill when shared data equals zero.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
3.6= − a/0.8 − 1.6 − 0.8 a −1.6
Answers
The value of a for the given expression will be -3.31.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the expression is 3.6= − a/0.8 − 1.6 − 0.8 a −1.6. The value of a will be calculated as below,
3.6 = − a/0.8 − 1.6 − 0.8 a −1.6
3.6 + 1.6 + 1.6 = -a / 0.8 - 0.8a
6.8 = ( -a - 0.64a ) / 0.8
5.44 = -1.64a
a = -3.31
Therefore, the value of a will be -3.31.
To know more about an expression follow
https://brainly.com/question/388367
#SPJ1
Decide whether the rates are equivalent. Maria saves $50 in 4 months.
Ralph saves $60 in 5 months
Answers
Answer:
The rates are not equivalent since Maria saves $0.50 more per month than Ralph.
Step-by-step explanation:
We can determine if two rates are equivalent by comparing the rates at which they save per month.
Maria's savings per month:
Both 50 and 4 can be divided by 2, which gives us 25/2. As a regular number, this becomes 12.5/1 which means Maria saves $12.5 per month.
Ralph's savings per month:
Both 60 and 5 can be divided by 5, which gives us 12. Thus, Ralph saves $12 per month.
Thus, the rates are not equivalent as Maria saves $0.50 more per month than Ralph.
Use the data set below to answer the following questions. 20 26 28 25 28 18 23 15 17 26 29 24 29 29 17 15 17 20 30 29 16 21 22 28 19
Approximately what percent of the data are greater than 28?
Approximately what percent of the data are less than 23?
Approximately what percent of data are greater than 17.5?
Approximately what percent of data are between 17.5 and 28?
Answers
Approximately 37.5% of the data are greater than 28, 33.3% of the data are less than 23, 91.7% of the data are greater than 17.5, and 62.5% of the data are between 17.5 and 28.
To answer the questions, we can analyze the given data set.
First, let's count the number of data points that satisfy each condition:
Greater than 28:
There are 9 data points greater than 28 (29, 29, 29, 30, 29, 29, 28, 28, 28).
Less than 23:
There are 8 data points less than 23 (20, 18, 15, 17, 17, 15, 17, 19).
Greater than 17.5:
There are 22 data points greater than 17.5.
Between 17.5 and 28:
There are 15 data points between 17.5 and 28.
Now, let's calculate the approximate percentage for each condition:
Percent greater than 28:
The total number of data points is 24. Approximately, 9 out of 24 data points are greater than 28.
Percentage =\((9 / 24) \times 100 = 37.5\)%.
Percent less than 23:
Approximately, 8 out of 24 data points are less than 23.
Percentage = \((8 / 24) \times 100 = 33.3\)%.
Percent greater than 17.5:
Approximately, 22 out of 24 data points are greater than 17.5.
Percentage = \((22 / 24) \times 100 = 91.7\)%.
Percent between 17.5 and 28:
Approximately, 15 out of 24 data points are between 17.5 and 28.
Percentage = \((15 / 24) \times 100 = 62.5\)%.
For more such questions on data
https://brainly.com/question/30459199
#SPJ8
You are dealt two card successively without replacement from a shuffled deck of 52 playing cards. Find the probability that the first card is a king and the second is a queen. Round to nearest thousandth
Answers
Answer:
0.078
Step-by-step explanation:
The probability P(A) of an event A happening is given by;
P(A) = \(\frac{number-of-possible-outcomes-of-event-A}{total-number-of-sample-space}\)
From the question;
There are two events;
(i) Drawing a first card which is a king: Let the event be X. The probability is given by;
P(X) = \(\frac{number-of-possible-outcomes-of-event-X}{total-number-of-sample-space}\)
Since there are 4 king cards in the pack, the number of possible outcomes of event X = 4.
Also, the total number of sample space = 52, since there are 52 cards in total.
P(X) = \(\frac{4}{52}\) = \(\frac{1}{13}\)
(ii) Drawing a second card which is a queen: Let the event be Y. The probability is given by;
P(Y) = \(\frac{number-of-possible-outcomes-of-event-Y}{total-number-of-sample-space}\)
Since there are 4 queen cards in the pack, the number of possible outcomes of event Y = 4
But then, the total number of sample = 51, since there 52 cards in total and a king card has been removed without replacement.
P(Y) = \(\frac{4}{51}\)
Therefore, the probability of selecting a first card as king and a second card as queen is;
P(X and Y) = P(X) x P(Y)
= \(\frac{1}{13} * \frac{4}{51}\) = 0.078
Therefore the probability is 0.078
exponential function passes through (1,10) and (4,80)
Answers
Answer: f(x)=2^x+5
Step-by-step explanation:
math
What is 1/3 time's 12 pls help me.
Answers
Answer:
4
Step-by-step explanation:
1/3 x 12= 4
Identify the equation in slope-intercept form for the line with the given slope that contains the given point.
Slope =4; (6,−5)
Answers
Answer:
The equation would be -5=4(6)+ b
Step-by-step explanation:
Answer:
y = mix + b where m is the slope, and b is the y- intercept. solution
What is the solution to the equation
2x=5
Answers
Answer:
5/2 or 2.5
Step-by-step explanation:
Divide both sides by 2.
Determine whether the given segments have the same length. Drag and drop each number
into the correct box to complete the justification of your answer. BC and EF

Answers
Answer:
Step-by-step explanation:
Length of a segment between two points \((x_1,y_1)\) and \((x_2,y_2)\) is given by the formula,
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Coordinates of extreme ends of BC and EF are,
B(1, 4), C(3, -2), E(-3, -2) and F(-1, 1)
Length of BC = \(\sqrt{(1-3)^2+(4+2)^2}\)
= \(\sqrt{4+36}\)
= \(2\sqrt{10}\) ≈ 6.32 units
Length of EF = \(\sqrt{(-3+1)^2+(-2-1)^2}\)
= \(\sqrt{4+9}\)
= \(\sqrt{13}\) ≈ 3.61 units
The length of BC is 6.32. The length of EF is 3.61.So, BC and EF don't have the same length.
please see picture for question

Answers
Question provided in attachment.

Answers
We can be 99% confident that the true mean healing rate of newts falls within the interval of 22.919 to 30.415 micrometers per hour.
How to calculate the valueSample Mean: = (29 + 27 + 34 + 40 + 22 + 28 + 14 + 35 + 26 + 35 + 12 + 30 + 23 + 18 + 11 + 22 + 23 + 33) / 18
= 480 / 18
≈ 26.667
Sample Standard Deviation (s):
= ✓((Σ(29 - 26.667)² + (27 - 26.667)² + ... + (33 - 26.667)²) / (18 - 1))
≈ ✓(319.778 / 17)
≈ ✓(18.81)
≈ 4.336
Confidence level = 99%
Sample Size (n) = 18
Sample Mean = 26.667
Sample Standard Deviation (s) = 4.336
Degrees of Freedom (df) = n - 1 = 18 - 1 = 17
Using a t-table or statistical software, we find that the critical value for a 99% confidence level with 17 degrees of freedom is approximately 2.898.
Margin of Error (E) = 2.898 * (4.336 / ✓18))
≈ 3.748
Confidence Interval = (26.667 - 3.748, 26.667 + 3.748)
= (22.919, 30.415)
We can be 99% confident that the true mean healing rate of newts falls within the interval of 22.919 to 30.415 micrometers per hour. This means that if we were to repeat the study multiple times and construct confidence intervals, approximately 99% of those intervals would contain the true mean healing rate of the population.
Learn more about confidence interval on
https://brainly.com/question/15712887
#SPJ1
Plssss helppppppl:((((

Answers
Answer:
I think it's 1.5 I'm not sure ._.
Answer:
1/3
Step-by-step explanation:
Total students = 36
No of boys = 24
No of girls = 36 - 24 = 12
Probability of selecting a girl = 12/36 = 1/3
The storage capability of computers has been doubling every 5 years since the first computers were invented in the 1960s. If the first computer could store .5 megabytes, about how many megabytes can today's computers store? How long did it take for computers to store 100 megabytes?
Answers
It takes time of near about 35 year.
Given that,
Storage capability of computers has been doubling every 5 years
The date of 1st computer made = 1980
computer could store 5 megabytes,
Now,
We can use the following calculation to determine how long it took computers to store 100 megabytes:
Therefore,
Log₂ (final amount / beginning amount)
= Log₂ (100 / 0.5)
= log₂ (200)
= 7.64 is the number of doublings.
If each doubling takes five years, then it would take computers just over seven doublings or almost 35 years to store 100 megabytes.
To learn more about exponential function visit:
https://brainly.com/question/14355665
#SPJ1
If you draw a card from a standard deck of 52 playing cards, what is the probability that it is a heart or a diamond?
Answers
Answer:
1/2
Step-by-step explanation:
In a deck of cards, there are 13 hearts and 13 diamonds
13+13 = 26 hearts or diamonds
P( hearts or diamonds) = numbers of hearts or diamonds / total
=26/52
= 1/2
why do the hands on the clock form an angle?
Answers
Answer:
The entire clock measures 360 degrees. As the clock is divided into 12 sections. The distance between each number is equivalent to 30 degrees (360/12)
I hope this helps you!
which number is IRRATIONAL

Answers
Answer:
C the square root of 15
Step-by-step explanation:
sqrt of 15 = 3.87298335...
Brainliest?
Find the value of x
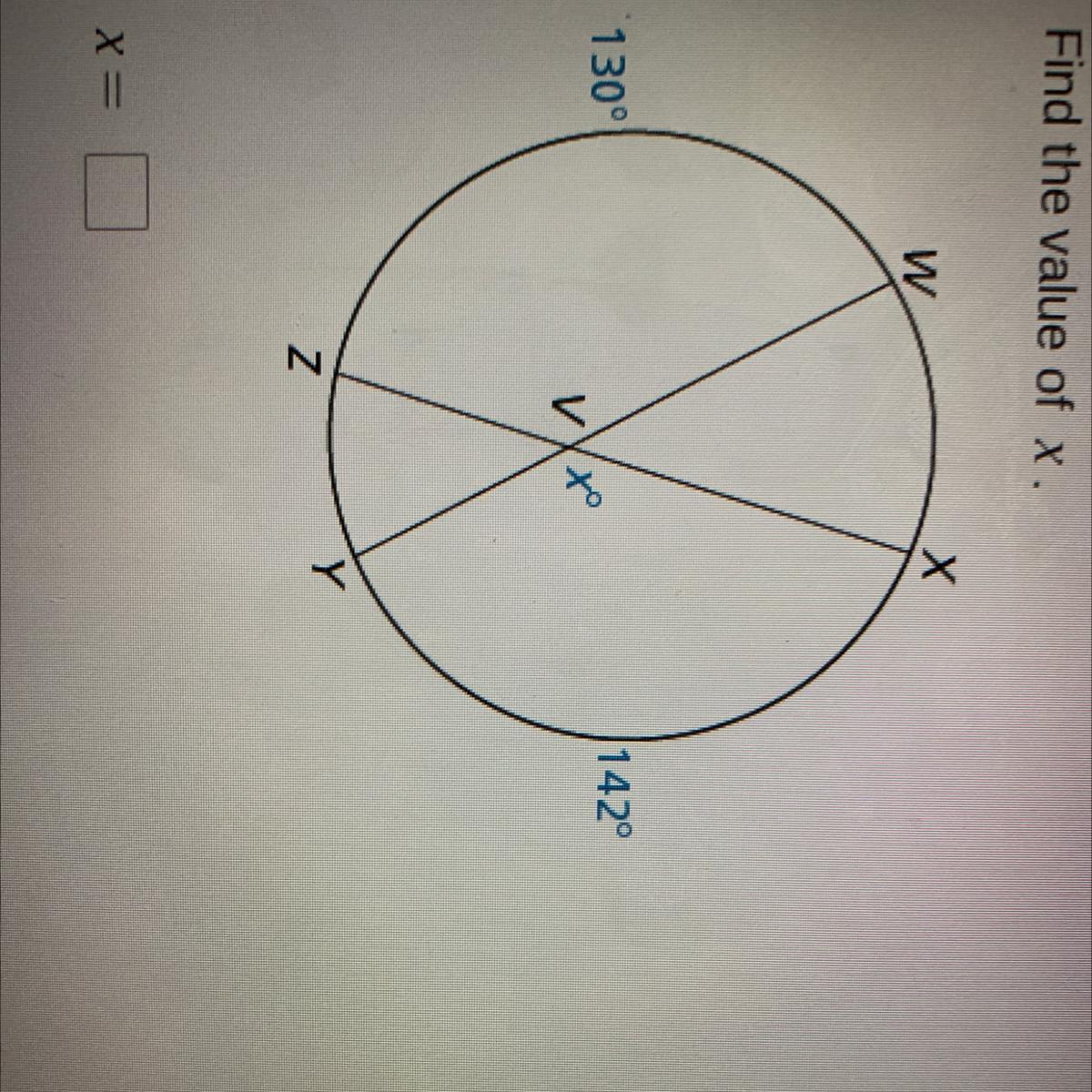
Answers
Answer:
136
Step-by-step explanation:
x = 1/2 (arc(XY) + arc(WZ) )
Arc (XY ) = 142
Arc(WZ) = 130
x = 1/2 (142 + 130)
x = 1/2 (272)
x = 136
Need help ASAP
the value of each variable. If your answer is not
teger, express it in simplest radical form.
The length of a is
The length of b is
(Simplify your answer.)

Answers
Answer:
me too (help)
Step-by-step explanation:
Sally collects stamps. Of all her stamps,
45% are from the United States. She has
90 stamps from the United States. How
many total stamps does she have?
Answers
Answer:
200 stamps
Step-by-step explanation:
Divide the 90 stamps by 45: The result is 2; it's equal to 1% of the total number of stamps. You then multiply it by 100 to get the full amount, which is 200 stamps.
90/.45=x/1.00
cross-multiply
.45x=90
x=200 stamps, dividing both sides by 0.45
+.45x+=+90+
+x+=+90%2F.45+
+x+=+200+
She has 200 stamps
So 200 stamps she has
Answer??????????????

Answers
Answer: 4/5 * 7^1/2 ==> 1st option
Step-by-step explanation:
3(7/25)^1/2-(28/25)^1/2+(63/25)^1/2=
3(7)^1/2 / 5 -(4*7)^1/2 / 5 +(9*7)^1/2 / 5=
3(7)^1/2 / 5 -2(7)^1/2 / 5 +3(7)^1/2 / 5=
(3-2+3)(7^1/2 / 5)=
4(7^1/2 / 5)=4/5 * 7^1/2 ==> 1st option
Please help! What is the surface area of the cylinder with height 4 m and radius 8 m? Round your answer to the nearest thousandth.
Make sure to round please.
Answers
The surface area of the cylinder is 948m²
What is surface area of cylinder?The area occupied by a three-dimensional object by its outer surface is called the surface area. The surface of a cylinder is expressed as ;
SA = 2πr(r+h)
Where r is the radius of the base and h is the height of the cylinder.
r =8m
h = 4m
SA = 2 × 3.14 × 8 (8+4)
SA = 78.96 × 12
SA = 947.52 m²
to the nearest whole number
SA = 948 m²
therefore the surface area of the cylinder is 948 m²
learn more about surface area of cylinder from
https://brainly.com/question/27440983
#SPJ1
make a triangular garden in the backyard. you know that one side of your yard (ac) is 100 yards long and another side (ab) is 250 yards. in order for the garden to fit and not cross into the neighbor's yard, what must be the measure of angle b if angel c measures 95 degrees?

Answers
Law of sines for the given triangle:
\(\frac{AC}{\sin B}=\frac{AB}{\sin C}\)Use the equation above and the given data to solve angle B:
\(undefined\)PLS HELP Find the opposite of the polynomial. -6x^(5)y^(2)z
A. −6x5y2z
B. 12x5y2z
C. −3x5y2z
D. 6x5y2z
Answers
Opposite of polynomial \(-6x^5y^2z = +6x^5y^2\) So, the correct answer is: D. \(6x^5y^2z\). Option D
The opposite of a polynomial is obtained by changing the sign of each term. In this case, we have the polynomial \(-6x^5y^2z\). To find its opposite, we change the sign of each term:
\(-6x^5y^2z\)
The coefficient -6 becomes +6, and we keep the same variables and exponents:
\(+6x^5y^2z\)
Therefore, the opposite of the polynomial\(-6x^5y^2z is +6x^5y^2z.\) Option D, \(6x^5y^2z,\)correctly represents the opposite of the given polynomial.
To summarize:
Opposite of \(-6x^5y^2z = +6x^5y^2z\)
So, the correct answer is:
D\(. 6x^5y^2z\) Option D
It's important to note that the other answer options provided (A, B, and C) are incorrect. Option A\((-6x^5y^2z)\) is the original polynomial itself, not its opposite. Option B \((12x^5y^2z)\)is not the opposite as it has a different coefficient (12 instead of -6). Option C \((-3x^5y^2z\)) is also not the opposite as it has a different coefficient (-3 instead of -6).
Thus, the correct answer is D. \(6x^5y^2z\), which represents the opposite of the given polynomial.
For more such questions on polynomial visit:
https://brainly.com/question/2833285
#SPJ8
Suppose the average of 15 consectutive numbers is 15. What is the average of the first five numbers of the set?
Answers
15x + 105= 225
15x= 225-105
15x= 120
X=8
X+ (x+1) + (x+2) + (x+3)…etc all the way up too +(x+14)=225
The first five numbers of the set: 8, 9, 10, 11, 12
I need this question to be solved please

Answers
Using the graphical method for limits, it is found that:
\(\lim_{x \rightarrow 3} f(x) = 1\)
What is a limit?A limit is given by the value of function f(x) as x tends to a value. In a graph, the lateral limits have to be equal, that is:\(\lim_{x \rightarrow a} f(x) = \lim_{x \rightarrow a^+} f(x) = \lim_{x \rightarrow a^-} f(x)\)
In this problem, the definition as x goes to 3 is the same, hence:
\(\lim_{x \rightarrow 3} f(x) = \lim_{x \rightarrow 3^+} f(x) = \lim_{x \rightarrow 3^-} f(x) = 1\)
You can learn more about limits at https://brainly.com/question/26270080
During the 2008 - 2009 financial crisis, the GDP of the USA reduced from $14.72 trillion in 2008 to $14.42 trillion in 2009. What is the percentage change between these two years? around your answer to the nearest hundredth of a percent.
Answers
The percentage change in GDP is 2.04%
Percentage ChangePercentage Change is the difference coming after subtracting the old value from the new value and then divide by the old value and the final answer will be multiplied by 100 to show it as a percentage. Generally, to convert a fraction into a percent, we multiply it by 100.
The formula of percentage change is given as
Percentage change =[ (New increase - old value) / old value] * 100
Percentage change = [(14.72 - 14.42) / 14.72] * 100
Percentage change = 2.04%
In this case, there is a percentage decrease of 2.04%
Learn more on percentage change here;
https://brainly.com/question/8728504
#SPJ1
The demand equation for a popular brand of fruit drink is given by the equation:
Qx=10-5px+0.001M + 10Py
where:
Qx= monthly consumption per family in liters
Px= price perlite of the fruit drink =$2.00
M= median annual family income =$20,000
Py= price per liter of a competing brand of fruit drink = $2.50.
1. Interpret parameter estimates.
2. Calculate the monthly consumptioliterslitres) of the fruit.
3. Suppose that the median annual family income increased to ¢30,000. How does this change your answer to part (b)?
4. Determine the demand function and the inverse demand function.
Answers
Answer:
Parameter estimates
The coefficient for Px (-5) suggests that there is an inverse relationship between the price of the fruit drink and the quantity demanded. In other words, as the price of the drink increases, the quantity demanded decreases.
The coefficient for M (0.001) suggests that there is a positive relationship between the median annual family income and the quantity demanded. In other words, as the median income increases, the quantity demanded also increases.
The coefficient for Py (10) suggests that there is a positive relationship between the price of the competing brand of fruit drink and the quantity demanded for this brand. In other words, as the price of the competing brand increases, the quantity demanded for this brand also increases.
Step-by-step explanation:
To calculate the monthly consumption of the fruit drink, we plug in the given values into the demand equation,
Qx = 10 - 5(2) + 0.001(20,000) + 10(2.5)
Qx = 10 - 10 + 20 + 25
Qx = 45 liters per family per month.
Therefore, the monthly consumption of the fruit drink per family is 45 liters.
If the median annual family income increased to $30,000, then the new monthly consumption of the fruit drink per family can be calculated as follows,
Qx = 10 - 5(2) + 0.001(30,000) + 10(2.5)
Qx = 10 - 10 + 30 + 25
Qx = 55 liters per family per month.
Therefore, the monthly consumption of the fruit drink per family would increase from 45 liters to 55 liters per family per month.
To determine the demand function, we need to solve for Qx in terms of the other variables,
Qx = 10 - 5Px + 0.001M + 10Py
Qx - 10Py = 10 - 5Px + 0.001M
Qx = (10 - 5Px + 0.001M) / 10Py
Therefore, the demand function is:
Qx = (10 - 5Px + 0.001M) / 10Py
To find the inverse demand function, we need to solve for Px in terms of Qx.
Qx = 10 - 5Px + 0.001M + 10Py
5Px = 10 - Qx - 0.001M - 10Py
Px = (10 - Qx - 0.001M - 10Py) / 5
Therefore, the inverse demand function is,
Px = (10 - Qx - 0.001M - 10Py) / 5
Please help!!
If you could explain how you solved this in detail it would be much appreciated.
When x^3+kx^2+2kx+6 is divided by (x-2), the remainder is 30. Find k.
Answers
Simplifying this equation, we get:
8 + 4k + 4k + 6 = 30
8k + 14 = 30
8k = 16
k = 2
Therefore, the value of k is 1.
What is polynomial?In mathematics, a polynomial is an expression consisting of variables (usually represented by x), coefficients, and non-negative integer exponents, which are combined using the operations of addition, subtraction, and multiplication. For example,
\(3x^2 + 2x - 1\)
is a polynomial with three terms, or a "trinomial," where the variable x is raised to the powers of 2 and 1, and the coefficients are 3, 2, and -1.
The degree of a polynomial is the highest power of the variable in the expression. For example, the polynomial above has a degree of 2, since the highest power of x is 2.
Polynomials are used in many areas of mathematics, including algebra, calculus, and geometry, and are used to model many real-world phenomena.
We can use the remainder theorem, which states that if a polynomial f(x) is divided by (x - a), then the remainder is equal to f(a). In this case, we know that when the polynomial\(l x^3 + kx^2 + 2kx\) + 6 is divided by (x - 2), the remainder is 30. So, we can set up the following equation:
\(x^3 + kx^2 + 2kx + 6 = (x - 2)q(x) + 30\)
where q(x) is the quotient when. \(x^3 + kx^2 + 2kx + 6\) is divided by (x - 2). We don't need to know what q(x) is, since we're only interested in finding k.
Now, let's substitute x = 2 into the equation above:
\(2^3 + k(2^2) + 2k(2) + 6 = (2 - 2)q(2) + 30\)
Simplifying the left-hand side, we get:
\(8 + 4k + 4k + 6 = 30\)
\(16k = 16\)
\(k = 1\)
OR
8 + 4k + 4k + 6 = 30
8k + 14 = 30
8k = 16
k = 2
To know more about equation visit:
https://brainly.com/question/10413253
#SPJ1