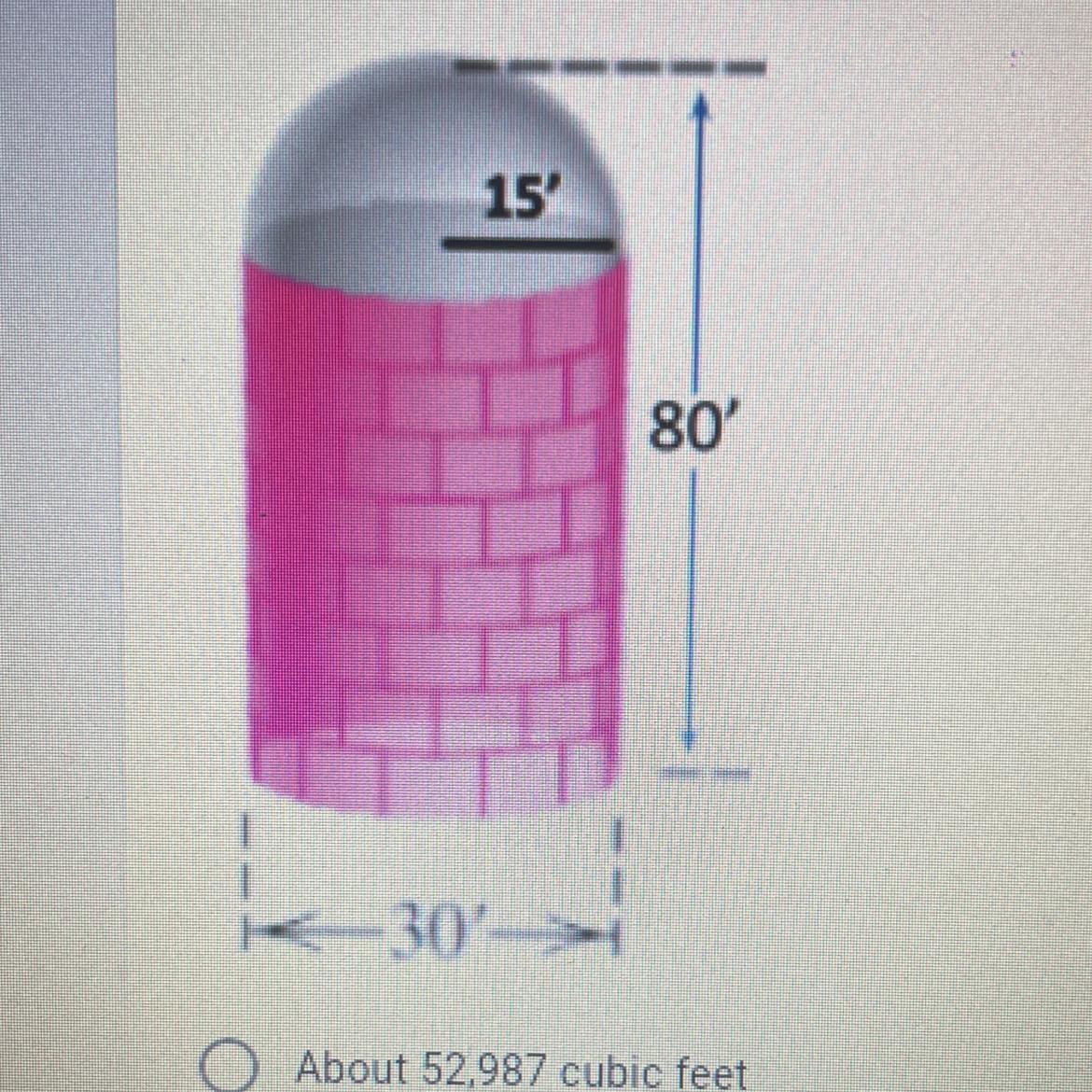
A large grain silo is to be constructed in the shape of a circular cylinder
with a hemisphere attached to the top. The diameter of the silo is to be 30 feet and the height is to be 80 feet. Calculate the total capacity of the
silo.

Answer:

22 is A

23 is A

24 is C

25 is B

Step-by-step explanation:

for #22, the equation is 108n = [(n - 2) × 180 degrees]. making that 108n = 180n - 360, then move the 180n to the other side to make 108n - 180n = 360. making that 72n = 360. That makes n = 5.

For #23, the equation would be (n - 2) × 180, n = 7, 7-2 = 5 and then 5 × 180 = 900 degrees.

For #24 the equation is 360/n, n = 5, meaning 360/5 would equal 72 degrees.

For #25, the equation would be 360/n, n = 22.5, meaning 360/22.5 would equal to 16 sides for each exterior angle.

The half-life period of a radioactive element is 7 days. The fraction of the radioactive element that disintegrates in 21 days is 0.406.

The half-life period of a radioactive element is 7 days.

Fraction of the sample will remain after 21 days:

The decay constant \(\lambda\) = \(\frac{0.693}{t_{1/2} }\)

= \(\frac{0.693}{7} = 0.099\)/ hour

t = 21 days

t = \(\frac{2.303}{\lambda} log\frac{a}{a-x}\)

21 = \(\frac{2.303}{0.099}log\frac{a}{a-x}\)

0.9028 = \(log\frac{a}{a-x}\)

2.466 = \(\frac{a}{a-x}\)

\(\frac{a-x}{a} =0.406\)

Hence,

The half-life period of a radioactive element is 7 days. The fraction of the radioactive element that disintegrates in 21 days is 0.406.

Find out more information fraction of the radioactive here

https://brainly.com/question/9561011

#SPJ4

The probability of having a 5-card hand that is a flush or royal flush is 0.00196

Probability: Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty.

Flush, straight flush, and royal flush probabilities are calculated as follows: 5148/2598960≅0.00198

A flush's likelihood (while eliminating straight and royal flushes) is 5108/2598960, ≅0.00196.

Finding the fraction with the number of ways to have a flush as the numerator and the number of possible five-card hands as the denominator will allow us to determine the likelihood.

Combinations will be used to find each of these numbers (we don't care about the draw order; only about what shows up in our hand). Combinations' general formula is Cn,k=n!/(k)!(n-k)! with k=picks and n=population

Let's first determine the denominator by selecting 5 cards at random from a deck of 52 cards: C52,5=52!/(5)!(525)!

=52!/(5!)(47!)

Let's assess it!

52×51×50^10×49×48^2×47!/5×4×3×2×47!=52×51×10×49×2=2,598,960

Let's now determine the numerator.

In order to examine each hand with five cards of the same suit, we will compute all hands that feature a flush (including straight flushes, royal flushes, and flushes) (with a suit having 13 cards in total). We can say that we understand this by:

C13,5

Remember that there are 4 suites in which this might occur, but we only want 1, so multiply by C4,1. Putting it all together, we obtain:

C4,1×C13,5=4!/(1!)(4−1)!×13!/(5!)(13−5)!=4!13!/3!5!8!

Let's assess this.

4!×13×12×11×10×9^3×8!/3×2×5×4!×8!=13×12×11×3=5148

(Remember that we just calculated all hands, including straight flushes and royal flushes, that have a flush component to them!

The probability of getting a hand with a flush is:

5148/2598960≅.00198

We may exclude straight and royal flush possibilities from the 5148 flush hands by excluding those hands (which are hands with 5 consecutive value cards in the same suit, such as 3, 4, 5, 6, and 7 of hearts). Since there are four suits and 10 potential ways to get a straight (A-5, 2-6, 3-7,..., 10-A), we can subtract 4 from 5148 to get 5108 hands, which gives us the result 5108/2598960=0.00196.

The probability of having a 5-card hand that is a flush or royal flush is 0.00196

To learn more about Probability visit:

brainly.com/question/11234923

#SPJ4

The product of the expression is 2x⁶ + 23x³ + 63

First, we should note that algebraic expressions are described as expressions that are composed of coefficients, terms, constants, variables and factors.

These algebraic expressions are also made up of mathematical operations, such as;

From the information given, we have that;

2x3 +9 and x3 +7?

Then,

(2x³ + 9)(x³ + 7)

expand the bracket

2x⁶ + 14x³ + 9x³ + 63

add like terms

2x⁶ + 23x³ + 63

Learn about algebraic expressions at: https://brainly.com/question/4344214

#SPJ1

(a) 95% confidence interval for the difference between female and male times is (11.954, 255.591).

(b) The assumptions and conditions for the two-sample t-test are met, so we can use the results of the test and confidence interval.

a) To construct a 95% confidence interval for the difference between female and male times, we can use a two-sample t-test. Let's denote the mean time for female swimmers as μf and the mean time for male swimmers as μm. We want to test the null hypothesis that there is no difference between the two means (i.e., μf - μm = 0) against the alternative hypothesis that there is a difference (i.e., μf - μm ≠ 0).

The formula for the two-sample t-test is:

t = (Xf - Xm - 0) / [sqrt((s^2f / nf) + (s^2m / nm))]

where Xf and Xm are the sample means for female and male swimmers, sf and sm are the sample standard deviations for female and male swimmers, and nf and nm are the sample sizes for female and male swimmers, respectively.

Using the data from the plots, we get:

Xf = 917.5, sf = 348.0137, nf = 15

Xm = 783.7273, sm = 276.0625, nm = 28

Plugging in these values, we get:

t = (917.5 - 783.7273 - 0) / [sqrt((348.0137^2 / 15) + (276.0625^2 / 28))] = 2.4895

Using a t-distribution with (15+28-2) = 41 degrees of freedom and a 95% confidence level, we can look up the critical t-value from a t-table or use a calculator. The critical t-value is approximately 2.021.

The confidence interval for the difference between female and male times is:

(917.5 - 783.7273) ± (2.021)(sqrt((348.0137^2 / 15) + (276.0625^2 / 28)))

= 133.7727 ± 121.8187

= (11.954, 255.591)

Therefore, we can be 95% confident that the true difference between female and male times is between 11.954 and 255.591 minutes.

b) Assumptions and conditions for the two-sample t-test:

Independence, We assume that the observations for each group are independent of each other.

Normality, We assume that the populations from which the samples were drawn are approximately normally distributed. Since the sample sizes are relatively large (15 and 28), we can rely on the central limit theorem to assume normality.

Equal variances, We assume that the population variances for the female and male swimmers are equal. We can test this assumption using the F-test for equality of variances. The test statistic is,

F = s^2f / s^2m

where s^2f and s^2m are the sample variances for female and male swimmers, respectively. If the p-value for the F-test is less than 0.05, we reject the null hypothesis of equal variances. If not, we can assume equal variances. In this case, the F-test yields a p-value of 0.402, so we can assume equal variances.

Sample size, The sample sizes are both greater than 30, so we can assume that the t-distribution is approximately normal.

To learn more about confidence interval here:

https://brainly.com/question/24131141

#SPJ4

Answer:

the mean

Step-by-step explanation:

mean is calculated average

Answer:

A: the mean

Step-by-step explanation:

Sorry for this very late response, but if anyone wasn't sure if answer A is correct, it is. I can confirm this because I just took the test, I hope I could help! (:

Answer:

yah yeet yeet yah

Step-by-step explanation:

The null hypothesis (H₀): p > 0.58

and the alternative hypothesis (\(H_A\)) :  p = 0.58

Also there isn't sufficient evidence at the 0.01 level of significance, that is, at a 1% level of significance, to refute the publisher's claim

Let us assume that p defines the population proportion of the publishers who own a personal computer.

Now, to test the claim, 58 % of their readers own a personal computer. (ex. p = 0.58)

This is be an alternative hypothesis and the null hypothesis proportion should be, p > 0.58

Now for this scenario,

the null hypothesis is H₀: p > 0.58

and the alternative hypothesis is \(H_A\):  p = 0.58

The newsletter publisher reject the null hypothesis.

Thus, the alternative hypothesis was accepted.

So, we can draw the conclusion: There isn't sufficient evidence at the 0.01 level of significance, that is, at a 1% level of significance, to refute the publisher's claim.

Learn more about the hypothesis here:

https://brainly.com/question/28920252

#SPJ4

The complete question is:

A newsletter publisher believes that 58% of their readers own a personal computer. Is there sufficient evidence at the 0.01 level to refute the publisher's claim?

State the null and alternative hypotheses for the above scenario.

Answer:

a. 1

Step-by-step explanation:

Replace 1 with x

2 ( 1 + 1 ) = 1 + 3

2 ( 2 ) = 1 + 3

4 = 1 + 3

4 = 4

Answer:

D, purple line.

Hope this helps!

Good luck with your finals!

Answer:

Gregor Mendel knew how to keep things simple. In Mendel's work on pea plants, each gene came in just two different versions, or alleles, and these alleles had a nice, clear-cut dominance relationship (with the dominant allele fully overriding the recessive allele to determine the plant's appearance

Step-by-step explanation:

ok intro dear new sis

Step-by-step explanation:

arithmetic sequence means that every new term is created by adding a certain constant (here 2) to the previous term.

a27 = -1/2 = a1 + (n-1)×2 = a1 + 26×2 = a1 + 52

a1 = -52 1/2 = -105/2

an = -105/2 + (n-1)×2

An independent variable influences change in another variable, known as the dependent variable. Correlation analyzes the relationship between variables, but causation requires experimental design and control.



A variable that influences change in another variable is called an independent variable. The independent variable is manipulated or controlled by the researcher in an experiment or study to observe its effect on the dependent variable. The dependent variable, on the other hand, is the variable being measured or observed, and it is expected to change in response to the manipulation of the independent variable.

The relationship between the independent and dependent variables can be analyzed through statistical methods such as correlation analysis. Correlation measures the strength and direction of the relationship between two variables, indicating how changes in one variable correspond to changes in another. However, it's important to note that correlation does not necessarily imply causation. To establish a cause-and-effect relationship, experimental design and control are necessary to ensure that the observed changes in the dependent variable can be attributed to the manipulation of the independent variable.



Therefore, An independent variable influences change in another variable, known as the dependent variable. Correlation analyzes the relationship between variables, but causation requires experimental design and control.

To learn more about variable click here

brainly.com/question/15078630

#SPJ11

We will know the end behavior as follows:

There are 90 different outfits he can wear if he has to wear slacks and a shirt along with his 3 sport coats and 1 tie.

Here, we can use the multiplication principle of counting to determine the number of possible outfits a man can wear given that he must wear at least one pair of slacks and one shirt. Let us denote sport coats as A, B, and C; slacks as P1, P2, P3, P4, and P5; shirts as S1, S2, S3, S4, S5, and S6; and the tie as T.

Then, the number of outfits he can wear is given by the product of the number of choices for each item as follows: Total outfits = (Number of sport coats) × (Number of slacks) × (Number of shirts) × (Number of ties)= 3 × 5 × 6 × 1= 90. Differentiating between the cases where he wears only one shirt and one pair of slacks from those where he wears two or more of each is unnecessary because the problem statement requires that he wears at least one of each.

Therefore, we can calculate the total number of outfits directly using the multiplication principle of counting, which gives us the answer of 90 different outfits he can wear if he has to wear slacks and a shirt along with his 3 sport coats and 1 tie.

Learn more about multiplication principle here:

https://brainly.com/question/17514196

#SPJ11

Answer:

The answer to the inequality is \(p\geq 4\).

Step-by-step explanation:

Lets solve the inequality.

\(-2p\leq -8\)

Divide both sides of the equation by -2.

There is an inequality rule that says when multiplying or dividing both sides of an inequality by a negative value, flip the direction of the inequality sign.

First lets divide both sides by -2.

\(\frac{-2p}{2} \leq \frac{-8}{2}\)

Simplify the left side by cancelling the common factor of −2.

\(p\leq \frac{-8}{2}\)

Simplify the right side by dividing -8 by 2.

\(p\leq 4\)

We need to flip the direction of the inequality sign.

\(p\geq 4\)

The value of the approximation of the given integral is 50.2637.

By using the midpoint Rule with the given value of n to approximate the integral:

Given integral is ∫₂¹⁰√x²+3 dx for n=4.

Let, ∫ₙᵇf(x)dx=∫¹⁰₂√x2+3dx

Here, f(x)=√x²+3 and a≤x≤b→2≤x≤10.

The subintervals of length 2 are [xi−1,xi] = [2,4],[4,6],[6,8],[8,10].

According to the midpoint rule:

Simplify the expression:

Therefore, the value of the approximation of the given integral is 50.2637.

Know more about the midpoint rule here:

https://brainly.com/question/18315903

#SPJ4

The correct question is given below:
Use the Midpoint Rule with the given value of n to approximate the integral. Round the answer to four decimal places.

∫₂¹⁰√x²+3 dx, n=4

Answer:

The equation of the relationship is y = 1.25x + 6.5

Step-by-step explanation:

I graphed the ordered pairs on the graph below and found the slope and y-intercept of the line.

The price per game is $7.75. (If needed)

The lines "a" and "b" shown in the picture are parallel and crossed by a transversal line.

The angle that measures 65º and the adjacent angle to the one that measures (x+72)º are corresponding angles, which means that they are congruent.

Both adjacent angles are supplementary, which means that they add up to 180º

From this expression, you can determine the value of x, first, take the parentheses away and add the like terms:

Next, subtract 137 from both sides of the equation:

The value of x is 43 and the measure of the given angle is:

x+72 = 43+72 = 115º

The number of weeks required to reach the population of the city 3,000,000 people is equal to 80 weeks.

Current population of the city = 2,800,000

Increase in population per week = 2500

The final population of a city = 3000000

To find the number of weeks until the population reaches 3,000,000,

we can set up an equation based on the growth rate of the population.

Let us denote the number of weeks as 'w' and the initial population as 2,800,000.

The growth rate is given as 2,500 people per week.

The equation can be written as,

2,800,000 + 2,500w = 3,000,000

To solve for 'w' rearrange the equation and isolate the variable,

⇒2,500w = 3,000,000 - 2,800,000

⇒ 2,500w = 200,000

Now, divide both sides of the equation by 2,500 to solve for 'w'.

⇒ w = 200,000 / 2,500

⇒ w = 80

Therefore, it will take approximately 80 weeks for the population to reach 3,000,000 people.

Learn more about population here

brainly.com/question/27528841

#SPJ4

Answer: x = 135 degrees and y = 225 degrees.

Step-by-step explanation: To solve this problem we first use the equation (n-2)*180 [n being the number of sides] to find the sum of interior angles in the figure. We plug the values in: (8-2)*180 = 6*180 degrees = 1080 degrees. We divide this by 8 to get the measure of an interior angle: 1080 degrees/8 = 135 degrees. Since all the interior angles of a regular polygon are congruent, we can say that angle x + angle y = 360 degrees. Thus subtract x degrees from 360 degrees to get y: 360 degrees - 135 degrees = 225 degrees. Therefore, x = 135 degrees and y = 225 degrees.

Answer:

C, or D

Step-by-step explanation:

The answer is C, or D

Answer:

8 x + 14

Step-by-step explanation:

2(4x+7)

2×4x +2×7 =

8x+14

Answer:

I got 343.7

I realize you need three decimals but i dont know how

Step-by-step explanation:

what I did was multiply each of there density's with how much of the item they were given like for example 1.04 times 35 (because they are the same ingredient) and after I did the same with everything else and added them all up in the end

The solutions to the quadratic equation (x² + 10x + 21 = 0) are (x = -3) and (x = -7).

To solve the quadratic equation x² + 10x + 21 = 0 using the completing the square method, follow these steps:

1. Move the constant term to the other side of the equation:

x² + 10x = -21

2. Take half of the coefficient of x and square it:

\(\[\left(\frac{10}{2}\right)^2 = 25\]\)

3. Add the value obtained above to both sides of the equation:

x² + 10x + 25 = -21 + 25

x² + 10x + 25 = 4

4. Rewrite the left side of the equation as a perfect square:

(x + 5)² = 4

5. Take the square root of both sides of the equation:

\(\[\sqrt{(x + 5)^2} = \pm \sqrt{4}\]\\\)

\(\[x + 5 = \pm 2\]\)

6. Solve for x by subtracting 5 from both sides of the equation:

For (x + 5 = 2):

x = 2 - 5 = -3

For (x + 5 = -2):

x = -2 - 5 = -7

So, x = -7 and -3

To know more about completing the square method refer here:

https://brainly.com/question/13674062#

#SPJ11

We are given a function y = -4x^3 - 9x^11, and we need to find its first and second derivatives.

To find the first derivative, we apply the power rule and the constant multiple rule. The power rule states that the derivative of x^n is nx^(n-1), and the constant multiple rule states that the derivative of kf(x) is k*f'(x), where k is a constant. Applying these rules, we can find the first derivative of y = -4x^3 - 9x^11.

Taking the derivative term by term, the first derivative of -4x^3 is -43x^(3-1) = -12x^2, and the first derivative of -9x^11 is -911x^(11-1) = -99x^10. So, the first derivative of y is dy/dx = -12x^2 - 99x^10.

To find the second derivative, we apply the same rules to the first derivative. Taking the derivative of -12x^2, we get -122x^(2-1) = -24x, and the derivative of -99x^10 is -9910x^(10-1) = -990x^9. Therefore, the second derivative of y is d^2y/dx^2 = -24x - 990x^9.

To know more about derivatives click here: brainly.com/question/25324584

#SPJ11

Answer:

To compare who saves the most of their salary each month among Amy, John, and Emily, we need to calculate the amount of salary each person saves.

Let's assume that the monthly salary of each person is 'S'. Then we can calculate the amount saved by each person as follows:

Amy:

Amount saved = 20% of S = 0.2S

Amount spent = S - 0.2S = 0.8S

John:

Amount spent = 2/5 of S = (2/5)S

Amount saved = S - (2/5)S = (3/5)S

Emily:

Let's assume that Emily saves '5x' and spends '8x' of her monthly salary.

Then, according to the question, we have:

Amount saved = 5x

Amount spent = 8x

We know that the ratio of the amount saved to the amount spent is 5:8, so we can write:

Amount saved / Amount spent = 5/8

Substituting the values of amount saved and amount spent, we get:

5x / 8x = 5/8

5x = (5/8) x 8x

5x = 5x

Therefore, the ratio of amount saved to amount spent is equal to 5:8. This means that Emily saves 5/13 of her monthly salary and spends 8/13 of her monthly salary.

So, the amount saved by each person is:

Amy: 0.2S

John: (3/5)S

Emily: 5/13 of S

Now, we need to compare these amounts to find out who saves the most.

To compare these amounts, we can write them in terms of a common denominator:

Amy: 0.2S

John: (3/5)S = (0.6)S

Emily: (5/13)S = (0.3846)S (approx.)

Therefore, we see that John saves the most of his salary each month, followed by Amy and then Emily.

Working out:

Let's assume that each person earns $1000 per month.

Amy:

Amount saved = 20% of $1000 = $200

Amount spent = $800

John:

Amount spent = 2/5 of $1000 = $400

Amount saved = $1000 - $400 = $600

Emily:

Let's assume that Emily saves $5x and spends $8x of her monthly salary.

Then, we have:

Amount saved = $5x

Amount spent = $8x

We know that the ratio of the amount saved to the amount spent is 5:8, so we can write:

$5x / $8x = 5/8

Solving for x, we get:

x = 8/13

Substituting the value of x, we get:

Amount saved = $5 x (8/13) x $1000 = $384.62 (approx.)

Amount spent = $8 x (8/13) x $1000 = $615.38 (approx.)

Therefore, we see that John saves the most of his salary each month, followed by Amy and then Emily.

Answer: Event 2 is correct

Step-by-step explanation:

Event 2 I assume.

2/9 is kinda unlikely

The minimized SOP expression for F(A,B,C,D,E) using a five-variable Karnaugh map is D'E' + BCE'. A five-variable Karnaugh map is a graphical tool used to simplify Boolean expressions.

The map consists of a grid with input variables A, B, C, D, and E as the column and row headings. The cell entries in the map correspond to the output values of the logic function for the respective input combinations.

To find the minimized SOP expression, we start by marking the cells in the Karnaugh map corresponding to the minterms given in the function: 2m(4,5,6,7,9,11,13,15,16,18,27,28,31). These cells are identified by their binary representations.

Next, we look for adjacent marked cells in groups of 1s, 2s, 4s, and 8s. These groups represent terms that can be combined to form a simplified expression. In this case, we find a group of 1s in the map that corresponds to the term D'E' and a group of 2s that corresponds to the term BCE'. Combining these groups, we obtain the expression D'E' + BCE'.

The final step is to check for any remaining cells that are not covered by the combined terms. In this case, there are no remaining cells. Therefore, the minimized SOP expression for the given logic function F(A,B,C,D,E) is D'E' + BCE'.

Learn more about combinations here: https://brainly.com/question/29595163

#SPJ11

The t-value for a 98% confidence level with a sample standard deviation and 52 degrees of freedom is 2.03.

To calculate the t value for a 98% confidence level with a sample standard deviation and 52 degrees of freedom, we used the t-distribution table. The t-distribution table has two variables: degree of freedom and confidence level.

The first step was to locate the row in the table that corresponds to the given degrees of freedom (df=52). The next step was to locate the column in the table that corresponds to the given confidence level (98%). the t -value for the given df and CL was located at the intersection of the row and column, which is -2.03. essentially the t-distribution table provides a range of values for the amount of variability that is expected within a given sample.

The t-value is the point within the range that will represent the 98% confidence level for the sample with 52 degrees of freedom. the t-value of -2.03 indicates that the sample has a 9.8% chance of falling within a range of values that is two standard deviations away from the mean.

To know more about   confidence level  refer to the link brainly.com/question/22851322

#SPJ4