A ladder is leaning against a building forming a 25-degree angle with the building. If the ladder is 8 feet away from the building, how long is the ladder?
A: About 15 ft.
B: About 7.5 ft.
C: About 9 ft.
D: About 3 ft.
Answers
Answer: About 15 feet.
Step-by-step explanation: To solve this problem, we can use the Pythagorean theorem. The ladder forms the hypotenuse of a right triangle with the building and the ground, with the angle at the building forming the right angle. If the ladder is 8 feet away from the building, then the length of the ladder is the same as the length of the other leg of the triangle.
We can use trigonometry to find the length of this leg. In a right triangle, the tangent of an angle is equal to the length of the opposite side divided by the length of the adjacent side. In this case, the adjacent side is the length of the ladder and the opposite side is 8 feet, so we can write the following equation:
tan(25 degrees) = opposite side / adjacent side
tan(25 degrees) = 8 feet / adjacent side
To find the length of the adjacent side (the ladder), we can divide both sides of the equation by the tangent of 25 degrees:
adjacent side = 8 feet / tan(25 degrees)
According to my calculations, the length of the ladder is about 15 feet, so the correct answer is A: About 15 ft.
Related Questions
Simplify the expression and please show all work
-5+i over 2i
Answers
Answer:
2.5i
Step-by-step explanation:
-5/2 = 2.5
+i = 2.5i
Help, please! It's all in the screenshot

Answers
Answer:
cube root of 9. the third option
Step-by-step explanation:
x^3 = 9
we take the cube root of both sides.
so x = cube root of 9
6. The Gonzales family has three children. On summer break, they went to an amusement park. They bought 3 child tickets for $ 18.50 and 2 adult tickets. If they spent a total of $104.50, how much was the price of each adult ticket?
Answers
$18.50x3=$55.50
$104.50-$55.50=$49
Divide $49 by 2 because there are 2 adult tickets, each ticket is $24.50.
The um of two number i 66. Two time the leer number i 15 more than the greater number. What are the number
If x i a leer number, the equation i
Answers
The smallest number is 27 and the greater number is 39 when the smaller number is 15 more than the larger number twice.
Given that,
The smaller number is 15 more than the larger number twice.
We have to find what are the two numbers whose sum is 66.
We know that,
Let x = big number
Let y = small number
x + y = 66---->equation(1)
2y = x + 15---->equation(2)
We have to dins the x and y values
x+(x+15)/2=66
2x+x+15=66×2
3x+15=132
3x=132-15
3x=117
x=117/3
x=39
We take equation 2 and substitute x as 39
2y=x+15
2y=39+15
2y=54
y=54/2
y=27
Therefore, The smallest number is 27 and the greater number is 39 when the smaller number is 15 more than the larger number twice.
To learn more about number visit: https://brainly.com/question/17429689
#SPJ4
a data set consists of the data given below plus one more data point. when the additional point is included in the data set the sample mean of the resulting data set is 26.5. what is the value of the additional data point?23, 28, 20, 33, 42, 12, 19, 50, 36, 25, 19
Answers
The value of the additional data point is 36
To find the value of the additional data point, we can use the concept of the sample mean.
Given the data set: 23, 28, 20, 33, 42, 12, 19, 50, 36, 25, 19.
The sample mean of this data set is 26.5.
To find the value of the additional data point, we can use the formula for the sample mean:
(sample mean) = (sum of all data points) / (number of data points)
In this case, we have 11 data points in the original data set. Let's denote the value of the additional data point as x.
Therefore, we can set up the equation:
26.5 = (23 + 28 + 20 + 33 + 42 + 12 + 19 + 50 + 36 + 25 + 19 + x) / 12
Multiplying both sides of the equation by 12 to eliminate the fraction, we have:
318 = 282 + x
Subtracting 282 from both sides of the equation, we find:
x = 318 - 282
x = 36
Know more about sample mean here;
https://brainly.com/question/33323852
#SPJ11
.
What are the coordinates
of the midpoint, P, of QT
with endpoints Q(-2,-8)
and T(1,5)?
Thank you!
Answers
Answer:
(-1/2 , -3/2)
Step-by-step explanation:
midpoint formula:
(x₁ + x₂) / 2 , (y₁ + y₂) / 2
(-2 + 1) / 2 , (-8 + 5) / 2
P: (-1/2 , -3/2)
PLEASE HELP ASAP!!! I'LL MARK BRAINLIEST TO RIGHT ANSWER!!!

Answers
The solution of the inequality is, x ∈ (- ∞, 5) ∪ (10, ∞)
Where, x represent the number of totts.
What is Inequality?A relation by which we can compare two or more mathematical expression is called an inequality.
We have to given that;
My friend Raw has either no more than 5 toots and more than 10 toots.
Now, Let number of toots = x
Hence, We get;
⇒ x < 5
And, x > 10
Thus, The solution of the inequality is,
⇒ x ∈ (- ∞, 5) ∪ (10, ∞)
Learn more about the inequality visit:
https://brainly.com/question/25944814
#SPJ1
a company manufactures and sells shirts. the daily profit the company makes depends on how many shirts they sell. the profit, in dollars, when the company sells xx shirts can be found using the function f(x)
Answers
The company needs to sell at least 50 shirts in a day to cover its fixed costs and break even.
Assuming that the profit function is linear, we can write it in the form:
f(x) = mx + b
where x is the number of shirts sold, m is the profit margin per shirt, and b is the fixed cost (i.e., the profit made when no shirts are sold).
Let's say that the company's fixed cost is $500, and the profit margin per shirt is $10. Then the profit function can be written as:
f(x) = 10x + 500
To find the daily profit the company makes, we need to determine how many shirts the company sells in a day. Let's say that the company sells 100 shirts in a day. Then the daily profit is:
f(100) = 10(100) + 500 = $1,500
So, the company makes a profit of $1,500 when it sells 100 shirts in a day.
If we want to find the number of shirts the company needs to sell to break even (i.e., make zero profit), we can set the profit function equal to zero and solve for x:
0 = 10x + 500
-500 = 10x
x = -50
This means that the company needs to sell at least 50 shirts in a day to cover its fixed costs and break even.
Learn more about "profit function" : https://brainly.com/question/16866047
#SPJ11
Perform the indicated operations. Reduce the answers to lowest terms .

Answers
Step-by-step explanation:
1. (2+4+1)/9 = 7/9
2. 2 1/3 + 2/3 = 2 + (1+2)/3 = 2 + 3/3 = 2+1 = 3
3. 1 1/5 + 2 3/5 = 1+2 + 1/5 + 3/5 = 3 + (1+3)/5 =
3 4/5
4. 5/6 + 2/10 + 1/5 = 5/6 + 1/5 + 1/5 = 5/6 + 2/5
= (5×5)/(6×5) + (2×6)/(5×6)
= 25/30 + 12/30
= (25+12)/30
= 37/30 = 1 7/30
5. 3 1/2 + 4 2/3
= 3+4 + 1/2 + 2/3
= 7 + (1×3)/(2×3) + (2×2)/(3×2)
= 7 + 3/6 + 4/6
= 7 + (3+4)/6 = 7 7/6 = 8 1/6
6. 9/13 - 5/13 = (9-5)/13 = 4/13
7. 7 6/8 - 5 2/8
= (7-5) + (6/8 - 2/8)
= 2 + 4/8
= 2 1/2
8. 2/3 - 3/7
= (2×7)/(3×7) - (3×3)/(7×3)
= 14/21 - 9/21 = (14-9)/21 = 5/21
9. 11 1/5 - 5 4/5
= 10 6/5 - 5 4/5
= (10-5) + (6/5 - 4/5)
= 5 + 2/5 = 5 2/5
10. 15 4/5 - 7 7/10
= (15-7) + (4/5 - 7/10)
= 8 + (4×2)/(5×2) - 7/10
= 8 + 8/10 - 7/10
= 8 + 1/10
= 8 1/10
a pile of sand is cone-shaped. if the radius of the base is 5 feet and the altitude is 8 feet 10 inches, how many cubic feet of sand is in the pile?
Answers
The cone shaped pile can hold 235.5 feet sand.
What is volume of cone ?
One-third the sum of the area of the cone's circular base and its height is the formula for a cone's volume. Cones are described as pyramids with circular cross sections in terms of geometric and mathematical ideas. A cone's volume can be quickly determined by measuring the cone's height and radius.
Here radius of cone = 5 feet
Height of cone h = 8 feet 10 inches = 8+1 = 9 feet
Now volume of cone is
=> V = \(\pi r^2\frac{h}{3}\) cubic unit
=> V= 3.14* 25 * 3 = 235.5 cubic feet.
Hence the cone shaped pile can hold 235.5 feet sand.
To learn more about volume of cone
https://brainly.com/question/26738970
#SPJ4
Which ordered pair is a solution of the equation y = 10x?
A. (−6, −60)
B. (8, 90)
C. (8, 70)
D. (−10, −80)
Answers
Basically, you have to plug in your coordinate to the equation. Plug in -60 for y and -6 for x. Now it should look like:
-60 = 10(-6)
Multiply 10 by -6 to get:
-60 = -60
That is a true statement because -60 equals -60. So, A is a solution to the equation. Hope this helped!
Which line on the graph below has a slope of zero
P Q R S
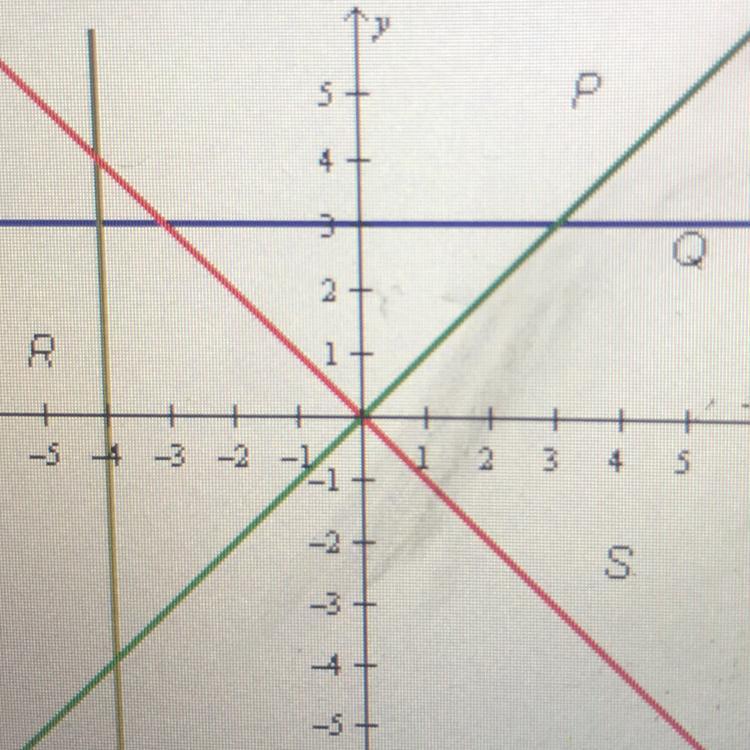
Answers
Kay used to have a square garage with 352ft of floor space. recently built an addition to it. The garage is still a square, but now it has 50% more floor space. What was the length of one side of the garage originally? What is the length of one side of the garage now? What was the percent increase in the length of one side?
Answers
Independent Practice
The equation k = 1.6d gives an approximate relationship between d miles and k kilometers. The distance between Columbus, Ohio, and Des Moines, Iowa, is 665 miles. Express the distance in kilometers.
A.
1,064 km
B.
415.6 km
C.
666.6 km
D.
663.4 km
Answers
\(k = 1.6d\)
\(k = 1.6(665)\)
\(k = 1064\)
The distance is 1064 km.
Answer:
A. 1,064 km
Step-by-step explanation:
1 Mile is 1,6 Kilometers
430 Miles = 688 Kilometers (430 * 1,6)
665 Miles = 1064 Kilometers (665 * 1,6)
1- 1.6(430)= 688 Km
2. 1.6(665)=1064 Km
Using 1.6 as the consant then 430* 1.6 = 688 Km
655 * 1.6 = 1048Km
if i understand what you need properly, all you do is multiply the miles x 1.6 and you will get k. so 430miles x 1.6 = 688k
and 665miles x 1.6 = 1064k
the image above is a _______?
a. rectangle
b. square and parallelogram
c. square
d. square and rectangle
e. parallelogram
f. square, rectangle and parallelogram

Answers
Answer:
F
Step-by-step explanation:
This is a square if you think about it, but it has the abilities of a rectangle and parallelogram. So it is F.
the diagram shows a partly filled oil tank the depth of oil present in the tank is 1.2m

Answers
Answer:
The quantity of oil in the tank is 12,000 liters
Step-by-step explanation:
Firstly, we find the volume of the tank.
The tank is a cuboid, so we find the volume of a cuboid.
Kindly understand that when finding the volume of the cuboid, we shall not use the height of 3m.
This is because the tank is not full but it is to a height of 1.2m
So mathematically, the volume is calculated as follows;
V = l * b * h
where b = 5m , l = 2m and h = 1.2m
Thus the volume would be ;
V = 5 * 2 * 1.2
V = 12 m^3
But that’s not the quantity of oil.
From the question, 1 cubic meters contains 1000 liters of oil
So 12 cubic meter will contain = 12 * 1000 = 12,000 liters of oil
Answer:
The quantity of oil in the tank is 12,000 liters
Step-by-step explanation:
Firstly, we find the volume of the tank.
The tank is a cuboid, so we find the volume of a cuboid.
Kindly understand that when finding the volume of the cuboid, we shall not use the height of 3m.
This is because the tank is not full but it is to a height of 1.2m
solve each equation for x )

Answers
Answer:
x= -13
Step-by-step explanation:
-1 -x = 12
+1 +1
-x = 13
-13 = x
I hope this helps :0)
Write an inequality that represents the missing dimension x.
The area is less than 18 square centimeters.

Answers
Answer:
x<3 cm²
Step-by-step explanation:
area of square: 4x
area of triangle: 1/2 (4x)=2x
total area: 6x
If the total area is less than 18:
6x<18
x<3
Inequality represents the missing dimension x is x<3.
Given that, the dimensions of the rectangle are length=4 cm and width=x cm.
The dimensions of the triangle are hieght=4 cm and base=x cm.
What is inequality?Inequalities are mathematical expressions in which both sides are not equal. In inequality, unlike in equations, we compare two values. The equal sign in between is replaced by less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign.
Now, the area of a figure> the area of a rectangle + the area of a triangle
18 cm²>length×width+1/2 × base × height
⇒18 cm²>4×x+1/2 × 4 × x
⇒18>4x+2x
⇒18>6x
⇒x<3
Therefore, inequality represents the missing dimension x is x<3.
To learn more about inequality visit:
https://brainly.com/question/20383699.
#SPJ2
The diameter of a circular cookie cake is 14 inches. How many square inches make up half of the cookie cake? Approximate using π = 3.14.
615.44 square inches
307.72 square inches
153.86 square inches
76.93 square inches
Answers
Answer:
Possibly A
Step-by-step explanation:
Answer:
76.93
Step-by-step explanation:
A clothing store donated a percent of every sale to hospitals. The total sales were $8,450 so the store donated $507. What percent of $8,450 was donated to hospitals?
Answers
Order the fractions from least to greatest. Type the number next to the fraction into the box for the position of the fraction in order.
5/8
1/3
17/24
Answers
From least to greatest
1. 17/24
2. 5/8
3. 1/3
Explanation: The fraction with the smaller denominator is the larger fraction
your sketching on a standard sheet of paper 8.5x11 in. if you draw a straight vertical line down half the width of the paper your line will be approximately
Answers
The line draw down as per given dimensions of standard sheet of paper 8.5x11 in then half the width of paper is 4.25 inches long approximately.
Let's consider a standard sheet of paper, which typically has dimensions of 8.5 inches by 11 inches (width by height).
If you draw a straight vertical line down half the width of the paper,
It is essentially drawing a line from the top edge to the bottom edge, dividing the paper into two equal halves.
The width of the paper is 8.5 inches.
When you draw a line down half the width, you are going from one edge to the midpoint.
Since you are going halfway, the length of the line will be half of the width,
which is 8.5 inches divided by 2, resulting in approximately 4.25 inches.
Therefore, the line you draw down half the width of the paper will be approximately 4.25 inches long.
learn more about width here
brainly.com/question/30282058
#SPJ4
HELP I WILL GIVE YOU BRAINLIEST PLS ASAP PLS HELP



Answers
Answer:
it is tetrahydrocannabinol for number 1 trust me
Step-by-step explanation:
HELP PLEASE ASAP!!!!!!!!
Brainliest goes to correct answer and 30 points given!!!!!

Answers
Answer:
lol lots of luck
Step-by-step explanation:
Matti is making moonshine in the woods behind his house. He’s
selling the moonshine in two different sized bottles: 0.5 litres
and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for
a
Answers
Based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
To solve the problem using the determinant method (Cramer's rule), we need to set up a system of equations based on the given information and then solve for the unknowns, which represent the number of 0.5 litre bottles and 0.7 litre bottles.
Let's denote the number of 0.5 litre bottles as x and the number of 0.7 litre bottles as y.
From the given information, we can set up the following equations:
Equation 1: 0.5x + 0.7y = 16.5 (total volume of moonshine)
Equation 2: 8x + 10y = 246 (total earnings from selling moonshine)
We now have a system of linear equations. To solve it using Cramer's rule, we'll find the determinants of various matrices.
Let's calculate the determinants:
D = determinant of the coefficient matrix
Dx = determinant of the matrix obtained by replacing the x column with the constants
Dy = determinant of the matrix obtained by replacing the y column with the constants
Using Cramer's rule, we can find the values of x and y:
x = Dx / D
y = Dy / D
Now, let's calculate the determinants:
D = (0.5)(10) - (0.7)(8) = -1.6
Dx = (16.5)(10) - (0.7)(246) = 150
Dy = (0.5)(246) - (16.5)(8) = -18
Finally, we can calculate the values of x and y:
x = Dx / D = 150 / (-1.6) = -93.75
y = Dy / D = -18 / (-1.6) = 11.25
However, it doesn't make sense to have negative quantities of bottles. So, we can round the values of x and y to the nearest whole number:
x ≈ -94 (rounded to -94)
y ≈ 11 (rounded to 11)
Therefore, based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
for such more question on litres
https://brainly.com/question/27877215
#SPJ8
Question
Matti is making moonshine in the woods behind his house. He’s selling the moonshine in two different sized bottles: 0.5 litres and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for a 0.7 litre bottle 10€. The last patch of moonshine was 16.5 litres, all of which Matti sold. By doing that, he earned 246 euros. How many 0.5 litre bottles and how many 0.7 litre bottles were there? Solve the problem by using the determinant method (a.k.a. Cramer’s rule).
ill mark brainliest, question is attached

Answers
Answer:
v = 7
Step-by-step explanation:
So, I used a go.ogle calculator for this, so I don't evidence, but here
hope this helps:)
Answer:
v=7
Step-by-step explanation:
\(3(3v-4)=51\\9v-12=51\\9v=51+12\\9v=63\\v=\frac{63}{9}\\v=7\)
Can someone please answer the questions

Answers
Answer:A. Most cats were in the 7th month and least in the 1st. B. Looking at the graph is legit straight up lit facts. C. I cannot justify the correlation. D. Well we could just kill off all the cars and be down with them falling out the stupid window or we can get them smarter owners
Step-by-step explanation:
In a two-year survey of 100 census tracts in Seattle (WA), Rountree and Warner (1999) observed a mean official violent crime rate of 27.06 per 1,000, with a standard deviation of 33.81. Construct a 95% confidence interval around this mean. What is the lower bound for this confidence interval
Answers
95% confidence that the true mean of the violent crime rate in Seattle's census tracts lies between 20.43 and 33.69 per 1,000.
In the given study, Rountree and Warner (1999) observed a mean official violent crime rate of 27.06 per 1,000 in 100 census tracts over a two-year period in Seattle, WA. The standard deviation was 33.81. To construct a 95% confidence interval around this mean, we can use the formula:
\(CI = mean ± (Z-score * (standard deviation / √sample size))\)
For a 95% confidence interval, the Z-score is 1.96. The sample size is 100 census tracts. So, we can calculate the interval as follows:
CI = 27.06 ± (1.96 * (33.81 / √100))
CI = 27.06 ± (1.96 * (33.81 / 10))
CI = 27.06 ± (1.96 * 3.381)
CI = 27.06 ± 6.63
The lower bound for this confidence interval is 27.06 - 6.63, which is approximately 20.43. Therefore, we can say with 95% confidence that the true mean of the violent crime rate in Seattle's census tracts lies between 20.43 and 33.69 per 1,000.
Learn more about confidence here:
https://brainly.com/question/29048041
#SPJ11
If 10% of a number is 16, find 5% of that number.
Answers
\(\text{If the number is x,}\\\\~~~~10\% \cdot x = 16\\\\\implies \dfrac{10x}{100} = 16\\\\\implies \dfrac x{10} = 16\\\\\implies x = 160\\\\\text{Hence,}~ 5\% \text{ of}~ 160 = \dfrac{5 \times 160}{100}=8\)
For what values of a does lim x→ar(x)=r(a) if r is a rational function?
Choose the correct answer below.
(a) Those values of a for which the denominator of the function r is not zero.
(b) Those values of a for which the numerator of the function r is zero.
(c) Those values of a for which the denominator of the function r is zero.
(d) Those values of a for which the numerator of the function r is not zero.
Answers
The correct answer is (d) Those values of a for which the numerator of the function r is not zero.
For a rational function r(x), the limit of r(x) as x approaches a can be determined by evaluating r(a) if the numerator of the function is not zero. This is because when the numerator is not zero, the limit of the function is defined and equal to the value of the function at that point.
However, if the numerator of the function is zero, then further analysis is required to determine the limit. In this case, the limit may be defined or undefined, depending on the behavior of the function as x approaches the point of interest.
In general, for a rational function, the limit exists and is equal to the value of the function at that point if and only if the numerator of the function is not zero at that point.
Learn more about numerator :
https://brainly.com/question/7067665
#SPJ4