a. JDJ b. Jpfe & G C dy dr, D: is bounded by y = 0, y = 4-², x=0, x=2. dx dy, D: is bounded by y = 2x, y=0, x= √In 3, y = 2√/ln 3. 2 du dr. D: is the circle x² + y² = 1.
Answers
The first integral is bounded by specific equations and involves integration with respect to x and y. The second integral is bounded by different equations the third integral is defined over a circular region.
In the first integral, JDJ, the region D is bounded by the equations y = 0, y = 4 - x², x = 0, and x = 2. To evaluate this integral, we need to perform a double integration with respect to x and y. The limits of integration for x are from 0 to 2, while the limits for y depend on the value of x. The function being integrated is not specified, so the integrand would need to be given in order to obtain the precise result.
In the second integral, Jpfe & G C dy dr, the region D is bounded by the equations y = 2x, y = 0, x = √ln 3, and y = 2√ln 3. Here, the integration is done with respect to y first and then with respect to x. The limits for y are determined by the given equations, while the limits for x are constant. The specific integrand is not provided, so further information would be required to compute the result accurately.
The third integral, 2 du dr, is defined over a circular region D given by the equation x² + y² = 1. This equation represents a unit circle centered at the origin. The integration is performed in polar coordinates, where u represents the angle and r denotes the radial distance. The limits for u would typically range from 0 to 2π, covering the entire circle, while the limits for r would depend on the radius of the circle involved in the problem. The integrand function is not specified, so the complete problem statement would be necessary to determine the exact result.
Learn more about integral here:
https://brainly.com/question/31059545
#SPJ11
Related Questions
Please somebody help me

Answers
Answer:
g = \(\frac{4}{3}\)
Step-by-step explanation:
4 - \(\frac{1}{12}\) g - 2 = \(\frac{3}{2}\) g + 1 - \(\frac{5}{6}\) g
multiply through by 12 ( the LCM of 12, 2 and 6 ) to clear the fractions
48 - g - 24 = 18g + 12 - 10g
- g + 24 = 8g + 12 ( subtract 8g from both sides )
- 9g + 24 = 12 ( subtract 24 from both sides )
- 9g = - 12 ( divide both sides by - 9 )
g = \(\frac{-12}{-9}\) = \(\frac{12}{9}\) = \(\frac{4}{3}\)
20.25 ➗ 0.9 standard form
Answers
The value of 20.25 ÷ 0.9 in standard form is 2.25×10¹
What is standard form?The standard form of a number is a way of writing the number in a form that follows certain rules. Any number that can be written as a decimal number, between 1.0 and 10.0, multiplied by a power of 10, is said to be in standard form.
This means that writing a value in the form 35.77× 10³ is very wrong in standard form because 35.77 is less than 10. But instead we write it in the form 3.577×10⁴, now 3.577 is less than 10.
The value of 20.25÷ 0.9 = 22.5
but this is not in standard form because 22.5 is greater than 10. By putting it in standard form, we divide it by 10 and multiply it by 10 again
This means that 22.5 = 2.25×10¹
Therefore 20.25 ÷ 0.9 in standard form is 2.25 × 10¹
learn more about standard form from
https://brainly.com/question/19169731
#SPJ1
if northwest airlines selects randomly a set of 40 flights on a given day, and then selects randomly a group of ten passengers on each of these flights to participate in an in-flight survey, the passengers are best referred to as a .
Answers
The passengers selected for the in-flight survey in this scenario can be best referred to as a stratified random sample.
In stratified random sampling, the population is divided into smaller, non-overlapping groups, called strata, which share similar characteristics. In this case, the strata are the 40 flights selected by Northwest Airlines. From each of these strata, a random sample of passengers is chosen, which in this case, is a group of ten passengers from each flight.
This method ensures that each flight's passengers are represented in the survey, allowing for better generalizability of the results. By selecting passengers randomly within each stratum, the survey helps minimize selection bias and ensures that the sample reflects the diversity of the overall population of passengers. The stratified random sampling approach is especially useful when studying a large and diverse population, as it provides a more accurate representation of the population's characteristics compared to simple random sampling.
In summary, the passengers participating in the in-flight survey are best referred to as a stratified random sample because they are chosen from 40 randomly selected flights, with ten passengers randomly selected within each flight. This sampling approach ensures better representation of the overall population and helps minimize selection bias in the survey results.
To know more about stratified random sampling, refer here:
https://brainly.com/question/29852583
#SPJ11
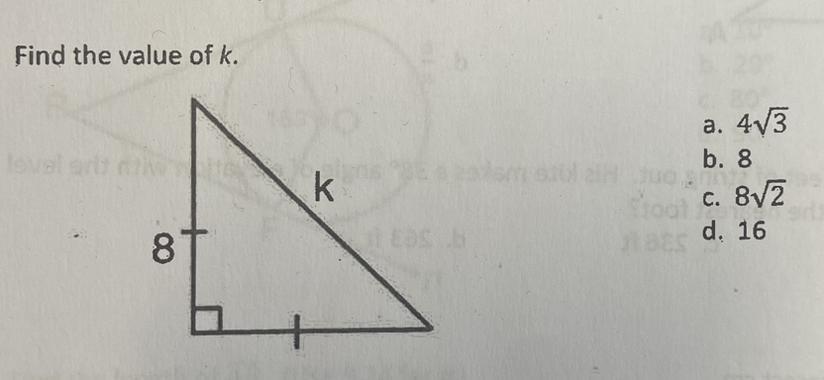
Find the value of k.
a.4√3
b. 8
c. 8√2
d. 16
Answers
Answer:
d. 8√2
Step-by-step explanation:
The 2 legs of the right triangle are shown as congruent.
k is the hypotenuse.
k² = 8² + 8² = 128
√k² = k = √128 = √64·2 = 8√2
Use polar coordinates to find the volume of the given solid.
Enclosed by the hyperboloid −x^2 − y^2 + z^2 = 6 and the plane z = 3
-x^2 - y^2 + 9 = 6 >>> x^2 + y^2= 3 so r2 = 3 >>> squart 0<=r <=3
My question is that why negative square root of 3 is not included in the range???
Answers
The negative square root of three is not included in the range since it correlates to negative radial distances.
The radial distance (r), which is always a non-negative value in polar coordinates, represents the distance from the origin to a point in the xy-plane.
The equation x2 + y2 = 3 denotes a circle with a radius of √3 and is centered at the origin. This equation can be expressed in polar coordinates as r2 = 3. It is impossible for r to be negative because it denotes the radial distance. Consequently, the range for r is 0 ≤ r ≤ √3.
Since it would correlate to negative radial distances, which are meaningless in the context of the issue and do not correspond to points inside the contained solid, the negative square root of three is excluded from the range.
To learn more about radial link is here
brainly.com/question/18405327
#SPJ4
Write the proportion. do not include units in the answer.
60feet is to 100feet as 12feet is to 20feet.
Answers
Answer:
(60/100) = (12/20)
Step-by-step explanation:

A company currently pays a dividend of $2.2 per share (D
0
=$2.2). It is estimated that the company's dividend will grow at a rate of 24% per year for the next 2 years, and then at a constant rate of 5% thereafter. The company's stock has a beta of 1.3, the risk-free rate is 9%, and the market risk premium is 4.5\%. What is your estimate of the stock's current price? Do not round intermediate calculations. Round your answer to the nearest cent.
Answers
The estimated current price of the stock is $57.83.
To calculate the stock's current price, we can use the dividend discount model (DDM). The DDM states that the price of a stock is equal to the present value of its future dividends.
In this case, the dividend is expected to grow at a rate of 24% per year for the next 2 years and then at a constant rate of 5% thereafter. We can calculate the dividends for the next two years as follows:
D1 = D0 * (1 + growth rate) = $2.2 * (1 + 0.24) = $2.728
D2 = D1 * (1 + growth rate) = $2.728 * (1 + 0.24) = $3.386
To find the price of the stock at the end of year 2 (P2), we can use the Gordon growth model:
P2 = D2 / (r - g) = $3.386 / (0.09 - 0.05) = $84.65
Next, we need to discount the future price of the stock at the end of year 2 to its present value using the required rate of return. The required rate of return is the risk-free rate plus the product of the stock's beta and the market risk premium:
r = risk-free rate + (beta * market risk premium) = 0.09 + (1.3 * 0.045) = 0.1565
Now, we can calculate the present value of the future price:
P0 = P2 / (1 + r)^2 = $84.65 / (1 + 0.1565)^2 = $57.83
Therefore, based on the given information and calculations, the estimated current price of the stock is $57.83.
Learn more about dividends here:
https://brainly.com/question/32150060
#SPJ11
How is 4.209 written using words?
Answers
Answer:
Four and two hundred nine thousandths
Answer
four and two hundred nine thousandths. or, simpler: four point two hundred nine. or, even simpler: four point two zero nine.
Step-by-step explanation:
Which of the following search algorithms should be used on large arrays if speed if important?
BinaryascendingBubble sortAll of the above
Answers
If speed is important and the array is large, the a. Binary search algorithm should be used. This algorithm is designed to efficiently search through sorted arrays by repeatedly dividing the search interval in half.
It has a time complexity of O(log n), which means that as the size of the array increases, the time it takes to search for an item will not increase at the same rate.
On the other hand, ascending bubble sort and other sorting algorithms such as selection sort and insertion sort have a time complexity of O(n^2), which means that as the size of the array increases, the time it takes to sort the array will increase exponentially. Therefore, these algorithms are not efficient for large arrays and should not be used if speed is important.
In summary, when dealing with large arrays and speed is important, binary search is the best algorithm to use for searching, while ascending bubble sort and other sorting algorithms with a time complexity of O(n^2) should be avoided.
To learn more about the Binary search algorithm, refer:-
https://brainly.com/question/29734003
#SPJ11
4. Explain the difference between (-5)2 anc
-52.

Answers
Answer: The answer is super easy bc it is only a small difference. The outcome of (-5)^2 will be 25 meanwhile -5^2 will have an outcome of -25
Answer:
(-5)² = 25 -5² = -25
Step-by-step explanation:
When we have (-5)², then -5 gets multiplied to itself. When there are two negative numbers, the answer is always positive. ex. (-5 x - 5 = 25)
(-5)² = 25
-5 x 5 = -25
-5² = -25
Solve (x^2 +xy)dy/dx=xy-y^2
Answers
The general solution to the differential equation is:
y = Cx^2 + x
where C is an arbitrary constant.
To solve the given differential equation:
x^2 + xy dy/dx = xy - y^2
We can start by rearranging it to get all the terms with y on one side and all the terms with x on the other side:
x^2 dy/dx + y^2 = xy - xy dy/dx
Now we can simplify both sides by factoring out a common factor of xy:
xy(dy/dx + 1) = y^2
Next, we can divide both sides by y(dy/dx + 1):
xy/y^2 = 1/(dy/dx + 1)
x/y = 1/(dy/dx + 1)
Cross-multiplying and simplifying:
dy/dx = (y-x)/x
This is a separable differential equation, which means we can separate the variables and integrate both sides:
dy/(y-x) = dx/x
Integrating both sides:
ln|y-x| = ln|x| + C
where C is the constant of integration.
Taking exponential of both sides:
|y-x| = e^C |x|
We can drop the absolute value signs since they cancel out when we square both sides:
(y-x) = Cx^2, where C is a constant.
Therefore, the general solution to the differential equation is:
y = Cx^2 + x
where C is an arbitrary constant.
Learn more about differential equation here:
https://brainly.com/question/32524608
#SPJ11
A restaurant offers three vegetable side dishes, two fruit side dishes, and five grain-based side dishes. Each entree comes with two side dishes. What is the approximate probability of randomly choosing one vegetable and one grain-based side dish? 0. 08889 0. 17778 0. 16667 0. 33333.
Answers
The approximate probability of randomly choosing one vegetable and one grain-based side dish from the available options is 0.16667.
To calculate the probability, we need to consider the number of possible outcomes and the total number of equally likely outcomes.
The restaurant offers three vegetable side dishes and five grain-based side dishes. For the first side dish, we have three vegetable options and five grain-based options. The probability of choosing a vegetable side dish first is 3/8, and the probability of choosing a grain-based side dish first is 5/8.
For the second side dish, after selecting one vegetable or grain-based side dish, we have two fewer options in that category. For the vegetable side dish, we would have two vegetable options remaining, and for the grain-based side dish, we would have four grain-based options remaining. Therefore, the probability of choosing a vegetable side dish as the second side dish is 2/7, and the probability of choosing a grain-based side dish as the second side dish is 4/7.
To find the probability of choosing one vegetable and one grain-based side dish, we multiply the probabilities of each step together: (3/8) * (4/7) = 12/56 ≈ 0.21429.
However, since we want the approximate probability, we can round the value to the nearest decimal place, which is 0.16667. Therefore, the approximate probability of randomly choosing one vegetable and one grain-based side dish is approximately 0.16667 or 16.67%.
Learn more about probability here:
https://brainly.com/question/32004014
#SPJ11
a class of 225 students,80 of them study Arabic only and 125 study french only. How many study both subjects.(venn diagram)
Answers
225-205=20
20 students study both subjects
Answer:
20
Step-by-step explanation:
225-80=145
145-125=20
Match the correlation to the statement:
I cannot be confident at all.
I can be a little confident; my prediction could be close or way off.
I can be somewhat confident; my predicted value could be close but not exact.
I can be certain that my predicted value will be exact.
-1 -0.645 0 0.347
Also If someone doesnt mind can you please explain this??? I dont understand at all lol.
Answers
The correct matching relating the correlation coefficients are given as follows:
0: I cannot be confident at all.0.347: I can be a little confident; my prediction could be close or way off.0.645: I can be somewhat confident; my predicted value could be close but not exact.-1: I can be certain that my predicted value will be exact.What is a correlation coefficient?A correlation coefficient is an index that measures the association between multiple variables.
The closer the absolute value of the correlation coefficient is of 1, the stronger is the association, meaning that the statement has more certainity.
Closer to zero, the correlation coefficient gives no confidence of the assessment, and values above 0.6 are considered as indicating strong correlation.
More can be learned about correlation coefficients at brainly.com/question/16355498
#SPJ1
QUESTION 24 1 POINT The radius of the wheel on a car is 20 inches. If the wheel is revolving at 346 revolutions per minute, what is the linear speed of the car in miles per hour? Round your answer to
Answers
The linear speed of the car in miles per hour is 71.39 mph.
The radius of the wheel on a car is 20 inches. If the wheel is revolving at 346 revolutions per minute, what is the linear speed of the car in miles per hour?Firstly, we can compute the distance travelled in one minute of the wheel's motion as:Distance = circumference of the wheel = 2πr.
Where r is the radius of the wheelWe know that the radius of the wheel, r = 20 inchesTherefore, distance travelled in one minute = 2π × 20= 40π inchesIf the wheel is revolving at 346 revolutions per minute, then distance travelled by the wheel in one minute = 40π × 346 = 13840π inches. One mile is equal to 63360 inches (by definition).Hence distance travelled by the wheel in one hour = 13840π × 60= 830400π inches per hourWe now convert from inches to miles:Distance travelled in one hour = 830400π ÷ 63360 miles/hour≈ 131.24 mph
Hence, the linear speed of the car in miles per hour is 71.39 mph (rounded to two decimal places).
To know more about linear speed visit :-
https://brainly.com/question/30397189
#SPJ11
Builtrite has calculated the average cash flow to be $14,000 with a standard deviation of $5000. What is the probability of a cash flow being between than $16,000 and $19,000 ? (Assume a normal distribution.) 16.25% 18.13% 23.90% 2120%
Answers
The correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
The probability of a cash flow between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
the table defines a discrete probability distribution. find the expected value of the distribution. x 0 1 2 3 pr(x) 3/16 3/16 1/8 1/2
Answers
To find the expected value of a discrete probability distribution, we multiply each possible outcome by its probability and then sum the products. In this case, we have:
E(X) = 0(3/16) + 1(3/16) + 2(1/8) + 3(1/2)
= 0 + 3/16 + 1/4 + 3/2
= 1.5
Therefore, the expected value of this distribution is 1.5.
In probability theory, the expected value (also known as the mean or average) of a discrete probability distribution is a measure of the central tendency of the distribution. It represents the theoretical long-term average of the values taken by a random variable over an infinite number of trials.
To find the expected value of a discrete probability distribution, we multiply each possible value of the random variable by its corresponding probability and add up the products. In other words, if X is a discrete random variable with possible values x1, x2, ..., xn and corresponding probabilities p1, p2, ..., pn, then the expected value E(X) is:
E(X) = x1 * p1 + x2 * p2 + ... + xn * pn
For example, consider the discrete probability distribution given in the table:
x | 0 | 1 | 2 | 3
pr(x) | 3/16| 3/16| 1/8 | 1/2
To find the expected value of this distribution, we multiply each possible value of X by its corresponding probability and add up the products:
E(X) = 0*(3/16) + 1*(3/16) + 2*(1/8) + 3*(1/2) = 0 + 0.1875 + 0.25 + 1.5 = 1.9375
Therefore, the expected value of this distribution is 1.9375.
To learn more about discrete probability distribution refer below
https://brainly.com/question/9602705
#SPJ11
Name all of the terms and factors in the expression: 3x2 + 8y + 6
Answers
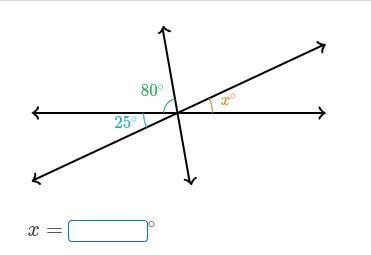
can you solve for the missing angle
Answers
Answer:
25°
Step-by-step explanation:
25° because opposite angles are equal
the blue angle 25° is opposite the yellow angle x° making x=25°
Answer:
x = 25°
Step-by-step explanation:
We can see that the 25° and x° are vertical to each other and vertical angles are angles that are the same size and directly opposite each other thus they are equal!
(ED. 21) Analytic Geometry Unit Test..... #3 Which point is a solution of x2 + y2 > 49 and y ≤ –x2 – 4?
Answers
Answer:
We want to find a solution of the system:
x^2 + y^2 > 49
y ≤ –x^2 – 4
Here we do not have any options, so let's try to find a general solution.
First, we can remember that the equation of a circle centered in the point (a, b) and of radius R is:
(x - a)^2 + (y - b)^2 = R^2
If we look at our first inequality, we can write it as:
x^2 + y^2 > 7^2
So the solutions of the first inequality are all the points that are outside (because the symbol used is >) of the circle of radius R = 7 centered in the origin.
From the other equation, we would get:
y ≤ –x^2 – 4
This is parabola, anything that is in the graph of the parabola or below will be a solution for this inequality.
Then the solutions of the system, are the ones that are in the region of solutions for both inequalities.
You can see the graph below, where both regions are graphed. The intersection of these regions is the region of the solutions for the system of inequalities:
by looking at the graph, we can see a lot of points that are solutions, like:
(0, -10)
(0, -15)
(2, -10)
etc.

Answer:
C on Edge or (1,-9)
Step-by-step explanation:
help asap assignment closes soon!

Answers
V = 1/3 b^2 • h
Plug in your values:
V = 1/3 (4)^2 • 9
Evaluate:
V = 1/3 (16) (9)
V = 48 ft^3
Hope this helps!
Answer:
48 ft^3
Step-by-step explanation:
Volume = (length x width x height)/3
V = (b times b times h)/3
V = (4 x 4 x 9)/3
V = 144/3
V = 48
(units: cubic feet --> 48 ft^3)
Find the selling price of a $20 item after a 20% markup.
Answers
Answer:
$24
Step-by-step explanation:
For a markup, use the formula a = ( 1 + p ) × w.
!!! Remember, a is the selling price, and w is the original price !!!
!!! The p is the percent in decimal form. 20% as a decimal is 0.20 (move the decimal twice to the left) !!!
Inserting the values, it should look like a = ( 1 + 0.20 ) × 20
a = 1.20 × 20
a = 24
Hence, the new selling price is $24.
Hope this helps! :)
A pack of 6 T-shirts costs $14.16. What is the unit price
Answers
6x = 14.16
x = 14.16 / 6
14.16 / 6 = 2.36
unit price = 2.36
A lottery consists of selecting 7 numbers out of 35 numbers. You win $10 if exactly three of your 7 numbers are matched to the winning numbers chosen. What is the probability of winning the $10?
Answers
the number of favorable outcomes is 35 * 20475 = 716,625.
Probability = 716,625 / (35! / (7!(35 - 7)!)).
To determine the probability of winning the $10 prize by matching exactly three numbers, we need to calculate the total number of possible outcomes and the number of favorable outcomes.
The total number of possible outcomes can be calculated using combinations. Since we are selecting 7 numbers out of 35, the total number of possible outcomes is given by the combination formula:
C(n, r) = n! / (r!(n - r)!)
In this case, n = 35 (total numbers) and r = 7 (numbers selected). Substituting these values into the formula:
C(35, 7) = 35! / (7!(35 - 7)!)
= 35! / (7!28!)
The number of favorable outcomes is determined by choosing 3 winning numbers from the 7 numbers selected and 4 non-winning numbers from the remaining 28 numbers. The number of favorable outcomes can be calculated using combinations as well:
C(7, 3) * C(28, 4)
Substituting the values into the formula:
C(7, 3) * C(28, 4) = (7! / (3!(7 - 3)!)) * (28! / (4!(28 - 4)!))
Calculating these values:
C(7, 3) = 7! / (3!(7 - 3)!)
= 7! / (3!4!)
= (7 * 6 * 5) / (3 * 2 * 1)
= 35
C(28, 4) = 28! / (4!(28 - 4)!)
= 28! / (4!24!)
= (28 * 27 * 26 * 25) / (4 * 3 * 2 * 1)
= 20475
Therefore, the number of favorable outcomes is 35 * 20475 = 716,625.
Now, we can calculate the probability of winning the $10 prize by dividing the number of favorable outcomes by the total number of possible outcomes:
Probability = Number of favorable outcomes / Total number of possible outcomes
= 716,625 / C(35, 7)
Calculating this value:
Probability = 716,625 / (35! / (7!(35 - 7)!))
It is important to note that calculating the factorial of 35 might result in very large numbers, which may be computationally intensive. Alternatively, you can use numerical methods or estimation techniques to approximate the probability.
Visit to know more about Probability:-
brainly.com/question/24756209
#SPJ11
6 root20+8 root5-5root45
Answers
Answer:
Step-by-step explanation:
\(6\sqrt{20} + 8\sqrt{5} -5\sqrt{45}\)
\(12\sqrt{5} + 8\sqrt{5} -15\sqrt{5}\)
\(5\sqrt{5}\)
Answer:
Step-by-step explanation:
I imagine that you are simplifying this, since there is nothing else you can do with it. You are in the section in algebra where you're learning how to simplify radicals. ALWAYS think prime factorization when it comes to numbers. For example, the square root of 5...the prime factorization of 5 is simply 5 * 1. So we know that √5 is as simple as it can be. It would benefit us if we could simplify either of the other 2 radicals down to the same radicand so we could add or subtract them.
The prime factorization of 20 is
20--> 5 * 4
4--> perfect square (2×2). So the simplification of 6√20 is 6×2√5 which is 12√5.
The prime factorization of 45 is
45--> 5 * 9
9--> perfect square (3×3). So the simplification of 5√45 is 5×3√5 which is 15√5.
Put it all together to get
12√5 + 8√5 -15√5 which simplifies to
5√5
7 2/9 + -5 1/5 =
show your work, show me how you got this answer pls double check!!!!!
D;
Answers

Solve: 4x < -16
A
B
C
D
X>4
X>12
X<-4
X <-20
Answers
Answer:
\( \: answer \: c = x < - 4\)
Marta walked at 2.9 miles per hour for 0.52 hours. How far did she walk?
Answers
CARD 3:
The original figure is dilated by a scale
factor of 2.5. What is the perimeter
of the new figure?
Who is correct?
Answers
Therefore, the perimeter of the new figure will be 2.5 times the perimeter of the original figure.
To find the perimeter of the new figure, we need to know its dimensions. Since the original figure is dilated by a scale factor of 2.5, the dimensions of the new figure will be 2.5 times the dimensions of the original figure.
Let's say the original figure has a perimeter of P units. Then the perimeter of the new figure will be:
P' = 2.5P
Therefore, the perimeter of the new figure will be 2.5 times the perimeter of the original figure.
Now, we don't have any information about the dimensions or perimeter of the original figure, so we cannot calculate the actual perimeter of the new figure.
As for who is correct, there is not enough information to determine that either. We would need to know the dimensions or perimeter of the original figure or have a diagram of the figures to compare.
In summary, to find the perimeter of the new figure, we need to know the dimensions of the original figure. Without that information, we cannot calculate the perimeter of the new figure or determine who is correct.
To know more about perimeter visit:-
https://brainly.com/question/6465134
#SPJ11
Find an equation of the line that passes through (3,10) and is parallel to the line x-3y=1
Answers
Answer:
x - 3y = -27
Step-by-step explanation:
Two parallel lines have equations of the same form; only the constants differ.
Thus, if the given line is x - 3y = 1, the desired new line has equation of the form x - 3y = C, where we must find the value of C.
Substituting 3 for x and 10 for y in x - 3y = C, we get 3 - 3(10) = C, or
3 - 30 = C. Thus, C = -27 and the desired new line is x - 3y = -27.