A golfer hits a 50g golf ball with a golf club that weighs 200g. At the point of impact, the golf club has a velocity of 100mph. assume the coefficient of restitution is 0.80. How fast is the ball moving after impact? (Show all work)
Answers
After the impact, the golf ball will be moving at approximately 73.13 mph.
To determine the velocity of the golf ball after impact, we can use the principle of conservation of momentum. The total momentum before the impact is equal to the total momentum after the impact.
Before the impact, the momentum is given by the sum of the momentum of the golf ball and the golf club. The momentum of an object is calculated by multiplying its mass by its velocity. The mass of the golf ball is 50g (0.05 kg) and the mass of the golf club is 200g (0.2 kg). The velocity of the golf club before impact is given as 100 mph, which is converted to m/s (1 mph = 0.447 m/s).
Using the conservation of momentum equation, we have:
(mass of golf ball * velocity of golf ball before impact) + (mass of golf club * velocity of golf club before impact) = (mass of golf ball * velocity of golf ball after impact) + (mass of golf club * velocity of golf club after impact)
Substituting the known values into the equation, we can solve for the velocity of the golf ball after impact. The coefficient of restitution (COR) is given as 0.80, which represents the ratio of the final velocity to the initial velocity of the golf ball. Rearranging the equation, we have:
velocity of golf ball after impact = (velocity of golf ball before impact - velocity of golf club before impact) * COR
Plugging in the values, we find that the velocity of the golf ball after impact is approximately 73.13 mph.
To learn more about Plugging click here
brainly.com/question/12126253
#SPJ11
Related Questions
almost every american adult has this thing
Answers
Answer: omm
but I need this so
Step-by-step explanation:
Danielle pays a monthly charge of $69 for her cable bill. She also pays a fee every time she watches a movie on demand. Last month danielle watched 7 movies on demand, and her total monthly bill was $104. Select from the drop-down menu to correctly complete each statement. The monthly charge for danielle's cable bill is choose. . Danielle also pays choose. Every time she watches a movie on demand.
Answers
Danielle viewed 7 movies on demand, thus you must divide her 35 dollars among them. So the monthly charge for Danielle's cable bill is $5.
Danielle pays a monthly charge of $69 for her cable bill.
She also pays a fee every time she watches a movie on demand.
Last month Danielle watched 7 movies on demand, and her total monthly bill was $104.
We have to find the monthly charge for Danielle's cable bill to choose.
Remove the monthly fee of 69 dollars for cable service from the total of 104 dollars, then check the statement to see that there is still a mystifying 35 dollars on it.
Danielle viewed 7 movies on demand, thus you must divide her 35 dollars among them, giving you the result of $5 per on-demand movie.
To learn more about Simplification link is here brainly.com/question/19691064
#SPJ4
The power generated by an electrical circuit (in watts) as function of its current x (in amperes) is modeled by: P(x)=-12x^2 +120x.
What current will produce the maximum power?
Answers
Given:
The power generated by an electrical circuit (in watts) as function of its current x (in amperes) is modeled by:
\(P(x)=-12x^2+120x\)
To find:
The current that will produce the maximum power.
Solution:
We have,
\(P(x)=-12x^2+120x\)
Here, leading coefficient is negative. So, it is a downward parabola.
Vertex of a downward parabola is the point of maxima.
If a parabola is \(f(x)=ax^2+bx+c\), then
\(Vertex=\left(\dfrac{-b}{2a},f(\dfrac{-b}{2a})\right)\)
In the given function, a=-12 and b=120. So,
\(-\dfrac{b}{2a}=-\dfrac{120}{2(-12)}\)
\(-\dfrac{b}{2a}=-\dfrac{120}{-24}\)
\(-\dfrac{b}{2a}=5\)
Putting x=5 in the given function, we get
\(P(5)=-12(5)^2+120(5)\)
\(P(5)=-12(25)+600\)
\(P(5)=-300+600\)
\(P(5)=300\)
Therefore, 5 watt current will produce the maximum power of 300 amperes.
The equation 4 cos x - 8 sin x cos x = 0 has two solutions in the interval [0, pi/2]. What are they? Smaller solution x = pi Larger solution x = pi
Answers
x = 5pi/6 is not in the interval [0, pi/2]
Starting with the given equation:
4 cos x - 8 sin x cos x = 0
We can factor out 4 cos x:
4 cos x (1 - 2 sin x) = 0
So either cos x = 0 or (1 - 2 sin x) = 0.
If cos x = 0, then x = pi/2 since we're only considering the interval [0, pi/2].
If 1 - 2 sin x = 0, then sin x = 1/2, which means x = pi/6 or x = 5pi/6 in the interval [0, pi/2].
So the two solutions in the interval [0, pi/2] are x = pi/2 and x = pi/6.
That x = 5pi/6 is not in the interval [0, pi/2].
for such more question on interval
https://brainly.com/question/22008756
#SPJ11
The given equation is 4 cos x - 8 sin x cos x = 0. To find the solutions in the interval [0, pi/2], we need to solve for x.
Find the solutions within the given interval. Equation: 4 cos x - 8 sin x cos x = 0
First, let's factor out the common term, which is cos x:
cos x (4 - 8 sin x) = 0
Now, we have two cases to find the solutions:
Case 1: cos x = 0
In the interval [0, π/2], cos x is never equal to 0, so there is no solution for this case.
Case 2: 4 - 8 sin x = 0
Now, we'll solve for sin x:
8 sin x = 4
sin x = 4/8
sin x = 1/2
We know that in the interval [0, π/2], sin x = 1/2 has one solution, which is x = π/6.
So, in the given interval [0, π/2], the equation has only one solution: x = π/6.
To learn more about factor : brainly.com/question/14209188
#SPJ11
Determine the solution for the following equation: (8x-8) 3/2 = 64
x = 3
x = 5
x = 13
x = 65
Answers
The correct answer is option A which is x = 3.
What is an expression?Expression in maths is defined as the collection of the numbers variables and functions by using signs like addition, subtraction, multiplication and division.
The expression will be solved as:-
( 8x - 8 )\(^\dfrac{3}{2}\) = 64
We can write 64 as \(16^{\dfrac{3}{2}}\)
( 8x - 8 )\(^\dfrac{3}{2}\) = \(16^{\dfrac{3}{2}}\)
8x - 8 = 16
8x = 24
x = 3
Therefore the correct answer is option A which is x = 3.
To know more about Expression follow
https://brainly.com/question/723406
#SPJ1
Answer:
A. x=3.
Step-by-step explanation:
Edge 2022.
Is 8+y=4x linear if yes what is standard form
Answers
Answer:4x-y=8
Step-by-step explanation:
It is linear
move y to the left side
8=4x-y
4x-y=8
find the constant solutions, if any, that were lost in the solution of the differential equation.
Answers
The given differential equation is y' - y = e^(2x). Find the constant solutions, if any, that were lost in the solution of the differential equation.Solution:We are given a differential equation: y' - y = e^(2x)This is a linear, first order differential equation.
The general solution of this differential equation can be found by first solving the homogeneous differential equation:y' - y = 0The solution to the homogeneous differential equation is y = Ce^x, where C is the constant of integration.Now, we solve for the particular solution to the non-homogeneous differential equation. The method of variation of parameters can be used to solve this non-homogeneous differential equation.y' - y = e^(2x)
First, we find the complementary function, which is the solution to the homogeneous differential equation:y_c = Ce^xThe particular solution to the non-homogeneous differential equation is of the formThus, the constant solution that was lost in the solution of the differential equation is y = 0, which is the solution to the homogeneous differential equation.
To know more about differential visit:
https://brainly.com/question/13958985
#SPJ11
help-
question : complete each of the following based on the relationship between square and square root.

Answers
Answer:
root 49= 7^2
root 100= 10^2
root 144= 12^2
root 324= 18^2
root 441= 21^2
Step-by-step explanation:
Find the value of x. Segments that appear to be tangent are tangent. Round your answer to the nearest tenth. Do not include "x=" in your answer.

Answers
The square of the hypotenuse is equal to the sum of the square of other two sides. The value of x from the given diagram to the nearest tenth is 11.2
Pythaogram theoremAccording to the theorem, the square of the hypotenuse is equal to the sum of the square of other two sides.
From the diagram
hypotenuse = 5.6 + 8.4 = 14
Other sides are x and 8.4
According to the theorem:
14^2 = x^2 + 8.4^2
x^2 = 14^2 - 8.4^2
Simplify
x^2 = 196 - 70.56
x^2 = 125.44
x = 11.2
Hence the value of x from the given diagram to the nearest tenth is 11.2
Learn moreon Pythagoras theorem here: https://brainly.com/question/18811544
Answer:
11.2
Step-by-step explanation:
just did it
What value of c will complete the square in the expression below to make it a perfect
square trinomial?
x² + 8x + c
Answers
Answer:
c = 16
Step-by-step explanation:
We have (a + b)² = a² + 2ab + b²
x² + 8x + c is of the form a² + 2ab + b²
where x² = a²
8x = 2ab
and c = b²
⇒ x² + 8x + c = (x + √c)² which is a perfect square
x² = a² ⇒ x = a
8x = 2ab
⇒ 8x = 2xb
⇒ b = 8x/(2x)
⇒ b = 4
c = b²
⇒ c = 4²
⇒ c = 16
(x + √c)² = (x + √16)²
= (x + 4)²
= x² + 2(x)(4) + 4²
= x² + 8x + 16
Therefore, c = 16 makes the expression a perfect square
Samia y su hija fueron a una obra de teatro musical, ella pago $90 por su boleto y $45 por el de su hija. Ese dia el cajerovendio 100 boletos y cuenta con $8190, pero necesita saber cuantos adultos y menores de edad entraron al evento?
Answers
Answer:
Al evento entraron 82 adultos y 18 menores de edad.
Step-by-step explanation:
De acuerdo a la información proporcionada, puedes plantear las siguientes ecuaciones:
x+y=100 (1)
90x+45y=8190 (2), donde:
x es el número de adultos
y es el número de menores de edad
Puedes despejar x en (1):
x=100-y (3)
Después, puedes reemplazar (3) en (2):
90(100-y)+45y=8190
9000-90y+45y=8190
9000-8190=90y-45y
810=45y
y=810/45
y=18
Ahora, puedes reemplazar el valor de y en (3) para encontrar x:
x=100-y
x=100-18
x=82
De acuerdo a esto, la respuesta es que al evento entraron 82 adultos y 18 menores de edad.
pls help me no links pls

Answers
Here's ur perfect answer

Someone please help me I’ll give out brainliest please dont answer if you don’t know
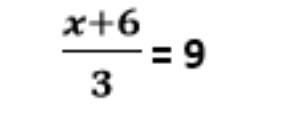
Answers
Answer:
21
Step-by-step explanation:
Clint is interested in making an offer on a house with hardwood floors that will need to be replaced. The hallway is 18 feet by 6 feet. The kitchen is 20 feet by 30 feet. The living room is 25 feet by 45 feet. There are two bedrooms, which measure 12 feet by 16 feet each, plus a master bedroom that is 14 feet by 20 feet. If the cost of the flooring is $5.48 per square foot, and the cost of installation is $1.49 per square foot, how much can Clint plan to spend to replace the floors
Answers
The amount of money Clint will plan to spend to replace the floors is $17404.09
How to find the cost to replace the floor?The hardwood floor is rectangular.
Therefore,
area of hallway = 18 × 6 = 108 ft²
area of the kitchen = 20 × 30 = 600 ft²
area of the living room = 25 × 45 = 1125 ft²
area of each bedroom = 12 × 16 = 192 ft²
area of master bedroom = 14 × 20 = 280 ft²
Hence,
cost of flooring per square foot is $5.48
total cost for flooring = 108(5.48) + 600(5.48) + 1125(5.48) + 192(5.48) + 192(5.48) + 280(5.48) = $13683.56
Cost of installation is $1.49 per square.
total cost of installation = 108(1.49) + 600(1.49) + 1125(1.49) + 192(1.49) + 192(1.49) + 280(1.49) = $3720.53
Total amount to replace the floor = 13683.56 + 3720.53 = $17404.09
Learn more about cost at: brainly.com/question/21394250
#SPJ4
A daycare center charges $300 per month for preschool and $3.50 per hour every hour after preschool. The function c = 300 + 3.50h can be used to represent the total cost c of monthly preschool and childcare, where h is the number of hours spent in childcare after preschool. If the one month charges for one child totaly $637.75, what was the total number of hours the child spent in childcare after preschool? *
Answers
Answer:
The total number of hours the child spent in childcare after preschool was 96.5.
Step-by-step explanation:
The cost of the preschool, in function of the number of hours that the child spent there, is given by the following equation:
\(c(h) = 300 + 3.5h\)
If the one month charges for one child totaly $637.75, what was the total number of hours the child spent in childcare after preschool?
This is h when c(h) = 637.75. So
\(c(h) = 300 + 3.5h\)
\(637.75 = 300 + 3.5h\)
\(3.5h = 337.75\)
\(h = \frac{337.75}{3.5}\)
\(h = 96.5\)
The total number of hours the child spent in childcare after preschool was 96.5.
If the area of a triangle is 16 units. And the base is 4, what is x?
Answers
Answer:
the area of triangle formula is A = B*H / 2 so it means 16 square = (x+4) x /2 so x²+4x -32=0, D' = 2²- (-32)= 36, sqrt of D' = 6 so x = -2 -6 = -8 or x= -2 +6 = 4 x must be positive so x = 4
Step-by-step explanation:
i really hoped this helped you.
5. Where is the graph increasing?

Answers
Answer:
Increases from points 0x,-6y to 2x,-3y.
Step-by-step explanation:
Consider the vectors: a=(1,1,2),b=(5,3,λ),c=(4,4,0),d=(2,4), and e=(4k,3k)
Part(a) [3 points] Find k such that the area of the parallelogram determined by d and e equals 10 Part(b) [4 points] Find the volume of the parallelepiped determined by vectors a,b and c. Part(c) [5 points] Find the vector component of a+c orthogonal to c.
Answers
The value of k is 1, the volume of the parallelepiped is 12 + 4λ, and the vector component of a + c orthogonal to c is (1,1,1.5).
a) Here the area of the parallelogram determined by d and e is given as 10. The area of the parallelogram is given as `|d×e|`.
We have,
d=(2,4)
and e=(4k,3k)
Then,
d×e= (2 * 3k) - (4 * 4k) = -10k
Area of parallelogram = |d×e|
= |-10k|
= 10
As we know, area of parallelogram can also be given as,
|d×e| = |d||e| sin θ
where, θ is the angle between the two vectors.
Then,10 = √(2^2 + 4^2) * √((4k)^2 + (3k)^2) sin θ
⇒ 10 = √20 √25k^2 sin θ
⇒ 10 = 10k sin θ
∴ k sin θ = 1
Therefore, sin θ = 1/k
Hence, the value of k is 1.
Part(b) The volume of the parallelepiped determined by vectors a, b and c is given as,
| a . (b × c)|
Here, a=(1,1,2),
b=(5,3,λ), and
c=(4,4,0)
Therefore,
b × c = [(3 × 0) - (λ × 4)]i + [(λ × 4) - (5 × 0)]j + [(5 × 4) - (3 × 4)]k
= -4i + 4λj + 8k
Now,| a . (b × c)|=| (1,1,2) .
(-4,4λ,8) |=| (-4 + 4λ + 16) |
=| 12 + 4λ |
Therefore, the volume of the parallelepiped is 12 + 4λ.
Part(c) The vector component of a + c orthogonal to c is given by [(a+c) - projc(a+c)].
Here, a=(1,1,2) and
c=(4,4,0).
Then, a + c = (1+4, 1+4, 2+0)
= (5, 5, 2)
Now, projecting (a+c) onto c, we get,
projc(a+c) = [(a+c).c / |c|^2] c
= [(5×4 + 5×4) / (4^2 + 4^2)] (4,4,0)
= (4,4,0.5)
Therefore, [(a+c) - projc(a+c)] = (5,5,2) - (4,4,0.5)
= (1,1,1.5)
Therefore, the vector component of a + c orthogonal to c is (1,1,1.5).
Conclusion: The value of k is 1, the volume of the parallelepiped is 12 + 4λ, and the vector component of a + c orthogonal to c is (1,1,1.5).
To know more about orthogonal visit
https://brainly.com/question/32250610
#SPJ11
Find the mean (average) of the following sets of numbers. a. 24, 45, 38, 56, 27 b. 24, 31, 17, 39, 9, 17 c. 125, 136, 174, 116, 164 d. 3.8, 9.2, 6.7, 11.5 e. 7.3, 7.5, 7.0, 8.1, 8.0
Answers
The term "mean" or "average" refers to a statistical measure that describes the central value of a set of data.
It is found by adding all the numbers in a set and dividing the sum by the total number of items in the set. The mean is a valuable tool in interpreting and comparing sets of data. Given below are the solutions to the problems presented:
a. Mean (average) = (24 + 45 + 38 + 56 + 27)/5= 190/5= 38
b. Mean (average) = (24 + 31 + 17 + 39 + 9 + 17)/6= 137/6= 22.83
c. Mean (average) = (125 + 136 + 174 + 116 + 164)/5= 715/5= 143
d. Mean (average) = (3.8 + 9.2 + 6.7 + 11.5)/4= 31.2/4= 7.8e.
Mean (average) = (7.3 + 7.5 + 7.0 + 8.1 + 8.0)/5= 38.9/5= 7.78
Therefore, the mean (average) of the given sets of numbers is:
a. 38 b. 22.83 c. 143 d. 7.8 e. 7.78
To know more about average refer to:
https://brainly.com/question/130657
#SPJ11
the measure of an angle is 44 more than the measure of its supplement. Find the measure of the angle.
Answers
How to Find Interquartile Range in Math with Examples?
Answers
The interquartile range (IQR) is a measure of variability in a dataset that is calculated as the difference between the third quartile (Q3) and the first quartile (Q1).
Quartiles divide a dataset into four equal parts, with Q1 representing the 25th percentile and Q3 representing the 75th percentile.
To find the interquartile range, you first need to find the values of Q1 and Q3. Here's an example:
Example:
Consider the following dataset of 11 numbers: 1, 3, 4, 6, 7, 9, 10, 13, 14, 18, 20.
First, we need to order the data in ascending order,
1, 3, 4, 6, 7, 9, 10, 13, 14, 18, 20
Next, we find the median of the entire dataset. Since there are 11 numbers, the median is the 6th number, which is 7.
We divide the dataset into two halves, the first half consists of the numbers below the median, and the second half consists of the numbers above the median. In this case, the first half is 1, 3, 4, 6, and 7, and the second half is 9, 10, 13, 14, 18, and 20.
We find the median of each half of the dataset. For the first half, the median is the average of the two middle numbers, which are 4 and 6. So Q1 = 5. For the second half, the median is the average of the two middle numbers, which are 13 and 14. So Q3 = 13.5.
Finally, we calculate the interquartile range by subtracting Q1 from Q3: IQR = Q3 - Q1 = 13.5 - 5 = 8.5.
So the interquartile range for this dataset is 8.5. This means that the middle 50% of the data is contained within a range of 8.5 units.
To learn more about interquartile range click on,
https://brainly.com/question/29173399
#SPJ4
during a car trip, tasha drives 65 miles per hour for several hours. she stops for gasoline, and then drives 40 miles more
Answers
Answer:
The total is 105 miles ..........,....
answer 4x + 1 = 9 what is x ?

Answers
Answer:
x=2
Step-by-step explanation
According to Euler, the buckling load for a column is given by P= xt 2
π 2
Et
. In this equation, the value of x for a column with one fixed end and the other end free is a) 1 b) 2 c) 4 d) 1/2
Answers
The theory behind Euler's equation and the boundary conditions for a column with one fixed end and the other end free. Therefore, the answer to the question is d) 1/2, as x = π/2L = (2(1) - 1)π/2L = (2n - 1)π/2L when n = 1/2.
Euler's equation is derived from the Euler-Bernoulli beam theory, which states that a slender column under axial compression will buckle when the compressive stress exceeds a certain critical value. The buckling load is given by the equation P= xt^2π^2Et, where P is the buckling load, x is a dimensionless factor called the slenderness ratio (the ratio of the column length to its cross-sectional dimensions), t is the thickness of the column wall, E is the modulus of elasticity of the column material, and π is the mathematical constant pi.
For a column with both ends pinned, the value of x is given by x = nπ/L, where n is an integer and L is the length of the column. For a column with one end fixed and the other end free, the value of x is given by x = (2n - 1)π/2L, where n is an integer. In this case, we have a column with one fixed end and the other end free, so we need to use the equation x = (2n - 1)π/2L to find the value of x. Since n can be any integer, we can choose n = 1 to simplify the equation and get x = π/2L.
Substituting this value of x into Euler's equation, we get P = (π/2L)²π²Et = π²Et/4L². This means that the buckling load for a column with one fixed end and the other end free is proportional to the modulus of elasticity and inversely proportional to the square of the length of the column.
Therefore, the answer to the question is d) 1/2, as x = π/2L = (2(1) - 1)π/2L = (2n - 1)π/2L when n = 1/2
To know more about Euler's visit:-
https://brainly.com/question/14091151
#SPJ11.
What is the missing length?

Answers
Answer:
16km
Step-by-step explanation:
Answer:
I REALLY hope I'm not wrong but I think it's 16
Step-by-step explanation:
I don't know I divided 224 by 14 to get 16.
To get an area you have to multiply length times width and the length is 14 so all you have to do if divide 224 by 14 to get your answer
Again, SO sorry if im wrong
find the volume of a pyramid with a square base, where the perimeter of the base is 5.7 cm 5.7 cm and the height of the pyramid is 8.6 cm 8.6 cm. round your answer to the nearest tenth of a cubic centimeter.
Answers
The volume of the pyramid is approximately 5.9 cm³.
What is the volume of pyramid?To find the volume of a pyramid with a square base, you can use the formula:
Volume = (1/3) * base area * height
First, let's find the area of the square base. The perimeter of the base is given as 5.7 cm, which means each side of the square has a length of 5.7 cm / 4 = 1.425 cm.
The area of a square is given by the formula:
Area = side length * side length
Substituting the side length, we have:
Area = 1.425 cm * 1.425 cm = 2.030625 cm²
Now, we can calculate the volume of the pyramid:
Volume = (1/3) * base area * height
= (1/3) * 2.030625 cm² * 8.6 cm
= 5.91834375 cm³
Rounding to the nearest tenth of a cubic centimeter, the volume of the pyramid is approximately 5.9 cm³.
Learn more about pyramid
brainly.com/question/13057463
#SPJ11
convolution, Fourier series representation problems
w 32. Use the convolution theorem to solve the integral equation: y(t) = ? + - sinhít – sinh(t - A)g()dx 33. Find the Fourier series representation of f(x) given that f(x) = -{: -1, - < x < 0 , 0
Answers
32. Solving integral equation using the convolution theoremThe convolution theorem states that the convolution of two signals in the time domain is equivalent to multiplication in the frequency domain.
Therefore, to solve the given integral equation using the convolution theorem, we need to take the Fourier transform of both sides of the equation.
y(t) = ∫_{-∞}^{∞} sinh(−)g() + ∫_{-∞}^{∞} sinh(−−)g()Taking the Fourier transform of both sides, we haveY() = 2π[G()sinh() + G()sinh(−)]where Y() and G() are the Fourier transforms of y(t) and g(t), respectively.Rearranging for y(t), we gety(t) = (1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)]e^(j) d= (1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)](cos()+j sin())d= (1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)]cos()d+ j(1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)]sin()dTherefore, the solution to the integral equation is given by:y(t) = (1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)]cos()d + (1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)]sin()d
It is always important to understand the principles that govern an integral equation before attempting to solve them. In this case, we used the convolution theorem to solve the equation by taking the Fourier transform of both sides of the equation and rearranging for the unknown signal. The steps outlined above provide a comprehensive solution to the equation. 33. Fourier series representation of f(x)
The Fourier series representation of a periodic signal is an expansion of the signal into an infinite sum of sines and cosines. To find the Fourier series representation of the given signal, we need to first compute the Fourier coefficients, which are given by:an = (1/T) ∫_{-T/2}^{T/2} f(x)cos(nx/T) dxbn = (1/T) ∫_{-T/2}^{T/2} f(x)sin(nx/T) dxFurthermore, the Fourier series representation is given by:f(x) = a_0/2 + Σ_{n=1}^{∞} a_n cos(nx/T) + b_n sin(nx/T)where a_0, a_n, and b_n are the DC and Fourier coefficients, respectively. In this case, the signal is given as:f(x) = -1, -π
To know more about integral visit
https://brainly.com/question/31433890
#SPJ11
Show that the series is convergent. How many terms of the series do we need to add in order to find the sum to the indicated accuracy
Answers
The total of five terms of the series we need to add in order to find the sum to the indicated accuracy.
What is convergent series?A series called convergent if the sequence of it's own partial sums tends to the a limit; that is, when addition one after the other with in order specified by the indices, partial sums become increasingly closer to a certain number.
Step1: The given series is a alternating series;
\(\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n^{6}}\)
where \(a_{n}=\frac{1}{n^{6}}\) is decreasing monotonically with n>1.
Thus, the given alternating series is convergent series.
As a result, we determine the smallest n such that; \(a_{n}\) < 0.00005.
Thus, it is concluded that the total of the series' first n-1 terms approximates the sum within in the allowed error.
Step 2: We must discover the smallest n such that,
\(\begin{aligned}\frac{1}{n^{6}} & < 0.00005 \\\frac{1}{n^{6}} & < \frac{5}{100000}\end{aligned}\)
Taking reciprocal both side,
Because both side is positive, the inequality is reversed.
\(\begin{aligned}n^{6} & > \frac{100000}{5} \\n^{6} & > 20000\end{aligned}\)
Use hit and trial to get the result.
\(\begin{gathered}a_{2}=2^{6}=64 \\a_{3}=3^{6}=729 \\a_{4}=4^{6}=4096\end{gathered}\)
\(\begin{gathered}a_{5}=5^{6}=15625 \\a_{6}=6^{6}=46656 \quad( > 20000)\end{gathered}\)
The smallest integer that fulfils this inequality gets satisfied is n=6.
As a result, n=6 is the lowest amount with an inaccuracy of less than 0.00005.
Therefore, to calculate the sum inside that allowed error, we simply have to add the very first five terms in the series.
To know more about convergent series, here
https://brainly.com/question/15415793
#SPJ4
The complete question is-
Show that the series is convergent. How many terms of the series do we need to add in order to find the sum to the indicated accuracy? \(\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n^{6}}\)
Find the next three terms in the sequence below.
\(\frac{21}{2} , \frac{19}{3}, \frac{17}{4} , 3, . . .\)
Answers
Answer: 13/6
Step-by-step explanation:
Based upon the previous sequence.
1.there is a constant decrease of two in the numerator
2. There is a constant increase of one in the denominator
to find the fourth number in the sequence I used One of the numbers from the previous to determine the answer.
17/4 — —> then I followed the pattern and determine what fraction 3 was . . before it was converted into a whole number.
which would be 15/5 —> Now considering equations that are written like this also mean division, because in this case division is possible the answer would be 3, which would make the whole number 3 instead of 15/3. considering it was an improper fraction.
____________________________________________________________
Now If 15/5 wasn’t converted into 3, The answer to the sequence would be 13/6. If you follow the pattern like I said before there is a certain amount of increase and decrease so 13/6 will be your answer. The only reason is not a whole number because 13 can’t be divided by six to get a whole number.
A rectangular hotel room is 3 meters by 8 meters. The owner of the hotel wants to recarpet the room with carpet that costs $33.38 per square meter. How much will it cost to recarpet the room?
Answers
The amount it will cost to recarpet the the whole room is $891.12
What is area ?The area of a shape is the space occupied by the boundary of a plane figures like circles, rectangles, and triangles.
For example, the area of a circle is given as: A = πr², where r is the radius and π is constant.
The room takes the shape of a rectangle, therefore,
Area of the room = l× w, where l is the length and w is the width.
Area = 3×8 = 24 m²
The cost of 1m² = $33.38
therefore the cost for 24m²
= 24× 33.8
= $801.12
therefore the cost to recarpet the room is $801.12
learn more about area from
https://brainly.com/question/25292087
#SPJ1