A glass prism on a chandelier is 93 millimeters long. A base of the prism is an equilateral triangle with side lengths of 7 millimeters and a height of about 6. 6 millimeters. What is the approximate surface area of the prism?
Answers
The approximate surface area of the glass prism is approximately 1986.66 square millimeters.
To find the surface area of the glass prism, we need to determine the area of each of its faces and then add them together. The prism consists of two congruent equilateral triangles and three rectangular faces.
The area of an equilateral triangle with side length s and height h is given by:
A = (√(3)/4) * s²
Using this formula, we can find the area of each of the two equilateral triangles in the prism:
A = (√(3)/4) * 7² ≈ 21.22 mm²
Next, we need to find the area of each of the three rectangular faces. The length of each rectangular face is equal to the side length of the equilateral triangle (7 mm), and the height is equal to the length of the prism (93 mm). Therefore, the area of each rectangular face is:
A = length x height = 7 mm x 93 mm = 651 mm²
To find the total surface area of the prism, we add the areas of the two equilateral triangles and the three rectangular faces:
Total surface area ≈ 2 x 21.22 mm² + 3 x 651 mm² ≈ 1986.66 mm²
Therefore, the approximate surface area of the glass prism is approximately 1986.66 square millimeters.
To know more about approximate surface area, refer to the link below:
https://brainly.com/question/879203#
#SPJ11
Related Questions
Can someone please help? I will mark brainliest random answers will be reported


Answers
Answer:
5.1
Step-by-step explanation:
hope it helps thank you
Mrs. Peabodys classroom was collecting
canned goods for a food drive. Her class set
a goal of collecting 300 cans. At the end of
the food drive, they collected 270 cans. What
percentage of their goal did they meet?
Answers
Answer:
570
Step-by-step explanation:
yan sagot ko ehh balakajan
pls help will give brainliest when i can

Answers
This is where one angle has the same relative position as another angle.
What’s the answer I need help pls?

Answers
Answer:
(E). y = 2cos(3x)
Step-by-step explanation:
First, amplitude of cos(x) is 1 , then 2cos(x) has amplitude 2
Second, period of cos(x) is 2\(\pi\) , then 3 × \(\frac{2\pi }{3}\) = 2\(\pi\)
So, the answer is y = 2cos(3x)
A customer wants an equity investment with a required rate of return of 7% and wants to receive a yearly dividend payment of $1.25. To meet the customer's requirements, the security must cost:
Answers
If customer wants an investment with rate of return of 7%, then to meet customer's requirements, the security must cost $17.86.
In order to find the cost of the security that meets the customer's requirements, we use the Dividend Discount Model (DDM). The DDM calculates the present value of future dividend payments based on the required rate of return.
The formula to calculate the cost of security is:
Cost of Security is = (Dividend)/(Required Rate of Return),
Substituting the values,
We get,
Dividend = $1.25
Required Rate of Return = 7% or 0.07 (in decimal),
So, the Cost-of-Security is = ($1.25)/(0.07) ≈ $17.86.
Therefore, the security must cost $17.86, in order to meet the requirement of customer.
Learn more about Investment here
https://brainly.com/question/29808903
#SPJ4
here is a scatter plot for a set of bivariate data. what would you estimate the correlation coefficient to be?
Answers
You can use scatter plots to present bivariate data. The data can be used to create coordinate pairs.
What is meant by scatter plot?The relationship between the two variables in a bivariate data set is graphically represented by a scatter plot. Consider them to be the graphic depiction of two data sets that have been combined by allocating each axis in the plot to a distinct variable.
Due to the presence of two variables, this type of data is known as bivariate data. Only 1 variable may be displayed on a line plot. You can use scatter plots to present bivariate data. The data can be used to create coordinate pairs.
The standard deviation of each variable and the covariance between them must first be determined in order to calculate the Pearson correlation. Covariance is subtracted from the product of the standard deviations of the two variables to get the correlation coefficient.
To learn more about scatter plot refer to:
https://brainly.com/question/6592115
#SPJ4
The temperature, C, in degrees Celsius recorded by a city park's weather station between midnight and 7:00 a.m. could be represented as a linear function of the number of hours after midnight, t. The temperature at 1:30 a.m. was −4.2°C and was −8.6°C at 7:00 a.m. Which equation could be used to represent this function?
Answers
Answer:
C(t)=−0.8t−3
Step-by-step explanation:
Trust
Ok, so I'm pretty sure this one is 11.5 I just wanted to make sure with u guys! :)

Answers
Answer:
C: 23 cm
Step-by-step explanation:
This is the answer because:
1) Area of trapezoid is: (base1 + base2)/2 x height
2) In this case, it is 14 + 8 which is 22. 22/2 is 11.
3) Now we have to do 253/11 which is 23 cm.
Hope this helps! :D
Answer:
no its C
Step-by-step explanation:
Can someone help me figure out how to do this?

Answers
What is the value of angle x°?

Answers
Answer:
\(64^\circ\)
Step-by-step explanation:
Please refer to the attached figure for the labeling and construction in the given figure:
Given that minor angle of arc AB is \(116^\circ\).
Or in other words, we can say that angle subtended on the center O by the arc is \(116^\circ\).
Now, PA and PB are the tangents so, if we join the center of circle O with A and B, the angles formed are right angles.
i.e.
\(\angle PAO = 90^\circ\\\angle PBO = 90^\circ\)
Now, we know that sum of internal angles of a quadrilateral is equal to \(360^\circ\).
Here, we have the quadrilateral AOPB.
\(\therefore \angle PAO +\angle PBO+\angle AOB +\angle APB=360^\circ\\\Rightarrow 90+90+116+x=360^\circ\\\Rightarrow x = 360 - 180 - 116\\\Rightarrow x = 64^\circ\)
Hence, the correct answer is:
\(x = 64^\circ\)

9-12x+6y apply the distributive property to factor out the greatest common factor of all three terms
Answers
To factor out the greatest common factor of the expression 9-12x+6y, we need to identify the greatest common factor of all three terms. The numbers 9, 12, and 6 have a common factor of 3, and the variables x and y have no common factors. Therefore, we can factor out 3 from each term using the distributive property.
9-12x+6y = 3(3-4x+2y)
This is the fully factored form of the expression, and we can see that the greatest common factor of all three terms is 3. By factoring out the greatest common factor, we simplify the expression and make it easier to work with.
To apply the distributive property and factor out the greatest common factor (GCF) of the terms in the expression 9 - 12x + 6y, follow these steps:
1. Identify the GCF of the coefficients (9, -12, and 6). The GCF is 3.
2. Factor out the GCF from each term: 3(3 - 4x + 2y).
3. The factored expression is now 3(3 - 4x + 2y).
By applying the distributive property and factoring out the GCF, we simplified the expression to its factored form, making it easier to work with in further calculations.
Learn more about distributive property here: brainly.com/question/32019808
#SPJ11
Line segment SU is dilated to create S'U' using the dilation rule DQ,2.5.
What is the distance, x, between points U' and U?
4 units
4.8 units
6 units
10 units

Answers
The distance between points U' and U is given as follows:
4.8 units.
What is a dilation?A dilation is defined as a non-rigid transformation that multiplies the distances between every point in a polygon or even a function graph, called the center of dilation, by a constant factor called the scale factor.
The equivalent distances are given as follows:
U' to U, S' to S.
Hence the distance between points U' and U is given as follows:
4.8 units.
A similar problem, also about dilation, is given at brainly.com/question/3457976
#SPJ1
The formula for finding the perimeter of a rectangle is p= 2l 2w solve the formula for w.
Answers
Answer:
w = \(\frac{p -2l}{2}\)
Step-by-step explanation:
p = 2l + 2w Subtract 2l from both sides of the equation
p - 2l = 2p Divide both sides by 2
\(\frac{p -2l}{2}\) = w
HELPEOEOOEOE HELP OELASDJ PLEASE
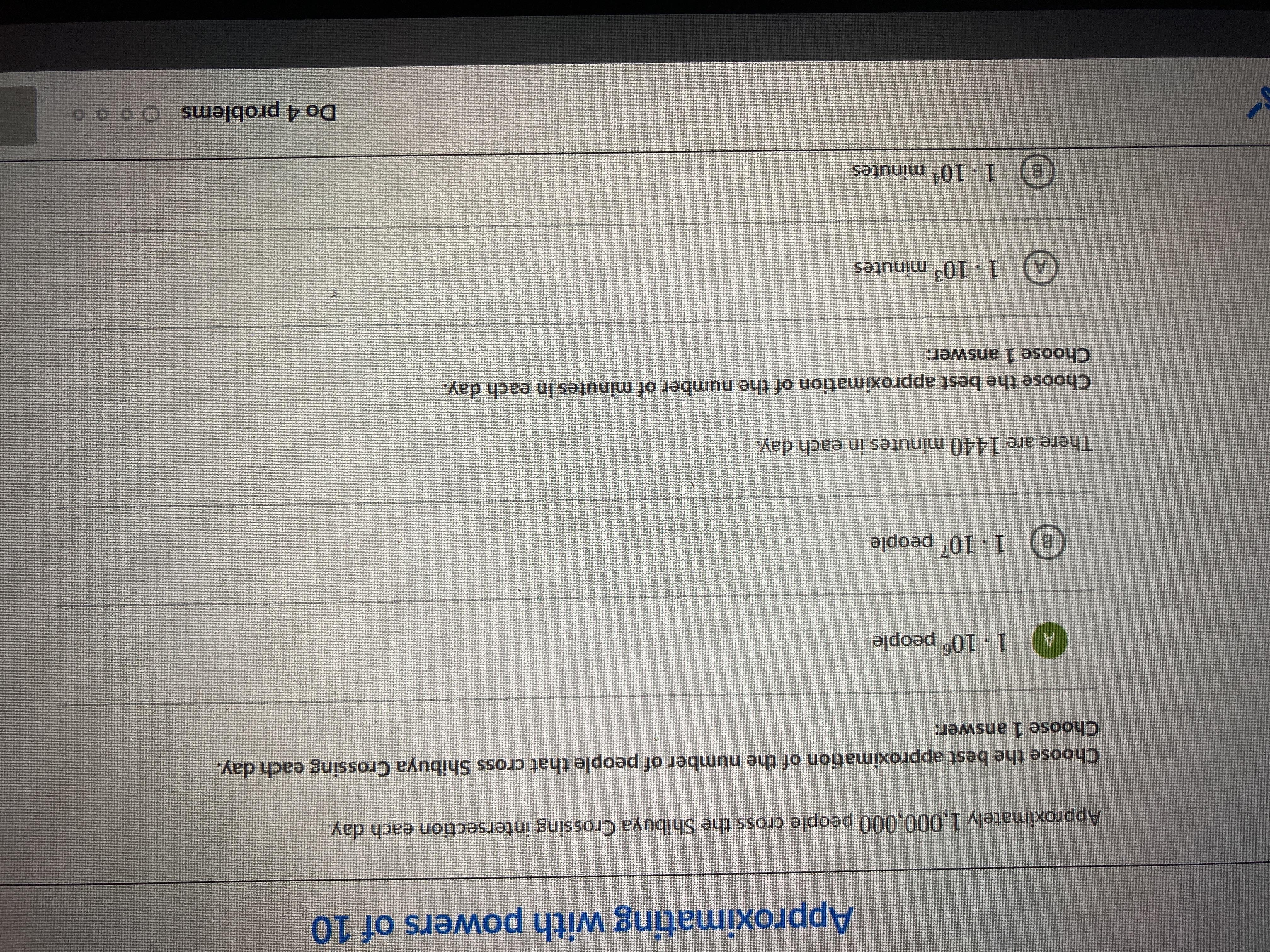

Answers
Answer:
A then B
Step-by-step explanation:
1440≈1,000, and 1,000=10^3
1000000/1440≈700, and 700≈1,000. 1,000=10^3
20% of a is 11. what is a
Answers
Answer:
2.2
Step-by-step explanation:
11*.20 = 2.2
So that is 20% on 11.
Hope this helps!
Hannah has liabilities totaling $30,000 (excluding her mortgage of $100,000 ). Her net worth is $45,000. What is her debt-to-equity ratio? 0.75 0.45 0.67 1.30 1.00
Answers
Hannah's debt-to-equity ratio when her liabilities was $30,000 (excluding her mortgage of $100,000 ) and her net worth is $45,000 is 0.75.
Debt-to-equity ratio is a financial ratio that measures the proportion of total liabilities to shareholders' equity. To calculate the debt-to-equity ratio for Hannah, we need to first calculate her total liabilities and shareholders' equity.
We are given that Hannah has liabilities of $30,000 excluding her mortgage of $100,000. Therefore, her total liabilities are $30,000 + $100,000 = $130,000.
We are also given that her net worth is $45,000. The net worth is calculated by subtracting the total liabilities from the total assets. Therefore, the shareholders' equity is $45,000 + $130,000 = $175,000.
Now we can calculate the debt-to-equity ratio by dividing the total liabilities by the shareholders' equity.
Debt-to-equity ratio = Total liabilities / Shareholders' equity = $130,000 / $175,000 = 0.74 (rounded to two decimal places)
Therefore, Hannah's debt-to-equity ratio is 0.74, which is closest to option 0.75.
Learn more about Debt-to-equity ratio here: https://brainly.com/question/27993089
#SPJ11
Find the value of x. If necessary, round to the nearest tenth.

Answers
Answer:
10.3 in
Step-by-step explanation:
a = (1/2)b*h
53 = (1/2)x * x
53 = (1/2)x²
Multiply both sides by 2
106 = x²
Take the square root of both sides
x = 10.3
Which of the following observations based on the graph is correct?
The cost of maintaining the machine is constantly rising.
No - "Constantly rising" means that there is never but an upward trend, but there is a flat spot and downward trend from 4 to 6 years.
For the first 3 years, it cost $300 to maintain the machine.
No - If true, the graph would be flat in the first 3 years, but it is rising. Only the 3rd years is the cost $300. The average rate of change between year 1 and year 4 is $500-$100/4 years = $400/year
No - The change in time from year 1 to year 4 is 3 years, not 4. And the $400/400 is $100/year.
The average rate of change between year 1 and year 4 is $500-
$100/(4-1) years = $400/3 years = $133.33 per year
Yes - Divide the change in wage by the change in time.
Answers
The average rate of change between year 1 and year 4 is $500-$100/(4-1) years = $400/3 years = $133.33 per year. This statement accurately calculates the average rate of change in cost.
To determine the correctness of the observations based on the graph, we need to carefully analyze the information presented.
Observation 1 states that the cost of maintaining the machine is constantly rising. However, this statement is incorrect as there is a flat spot and a downward trend from 4 to 6 years, indicating a decrease in maintenance costs during that period.
Observation 2 claims that the cost of maintenance is $300 for the first 3 years. This statement is also incorrect since the graph shows a rising trend in the cost during the first 3 years, and it is only in the third year that the cost reaches $300. The cost is not constant for the entire period.
Observation 3 states that the average rate of change between year 1 and year 4 is $400/400 = $100/year. This statement is incorrect because the change in time from year 1 to year 4 is actually 3 years, not 4. Therefore, the correct calculation would be $400/3 years, which is approximately $133.33 per year.
Learn more about cost and expenditure brainly.com/question/29886282
#SJP11
What is an open sentence in math? And how is it different from true or false?
Answers
An open sentence in math means that it uses variables, meaning that it is not known whether or not the mathematical sentence is true or false.
A closed sentence, on the other hand, is a mathematical sentence that is known to be either true or false
In a simple linear regression based on 30 observations, it is found that SSE- 2,540 and SST- 13,870 a. Calculate and se (Round your answers to 2 decimal places.) 5 b. Calculate the coefficient of determinationR. (Round your answer to 4 decimal places.) Coefficient of Determination
Answers
To calculate the standard error of estimate (SE), we can use the following formula:
SE = sqrt(SSE / (n-2))
where SSE is the sum of squared errors, and n is the number of observations.
Substituting the given values, we get:
SE = sqrt(2,540 / (30-2)) = 5.49
Therefore, the standard error of estimate is 5.49 (rounded to 2 decimal places).
b. The coefficient of determination (R-squared) is given by the ratio of the explained variation (SSR) to the total variation (SST):
R² = SSR / SST
where SSR is the sum of squared regression, and SST is the total sum of squares.
Since this is a simple linear regression, we have:
SST = SSR + SSE
where SSE is the sum of squared errors.
Substituting the given values, we get:
SST = 13,870
SSE = 2,540
Therefore, we can calculate SSR as:
SSR = SST - SSE = 13,870 - 2,540 = 11,330
Substituting these values into the formula for R-squared, we get:
R²= SSR / SST = 11,330 / 13,870 = 0.8188
Therefore, the coefficient of determination (R-squared) is 0.8188 (rounded to 4 decimal places). This means that 81.88% of the variation in the dependent variable (y) can be explained by the linear regression model with the independent variable (x).
To know more about standard error refer here:
https://brainly.com/question/13179711
#SPJ11
2 Gallons of Juice for $4.50. How much per Gallon?
Answers
4.50 divided by 2 is 2.25
Answer: 2.25 per gallon
Step-by-step explanation:
4.50 divided by 2 = 2.25
Will give brainliest, please answer

Answers
I got the rest done and now my brain Isn't cooperating, h e l p

Answers
1 x= 2
2 x= 16
3 x= 12
Heart or brainly me!
3. for questions 3-5, complete the missing values in each table below using the graph

Answers
The missing values are derived from the graph as follows:
3 ) 7, 14, 21, 28, 35
4) 3, 7, 10, 14, 17
5) 1, 21, 10, 49, 19
What is a graph?In mathematics, a graph is defined as a graphical representation or diagram that organizes facts or values. The graph's points frequently reflect the relationship between two or more objects.
In order to solve for the above values, the best way is to spot the function that exists in the graph which is given as:
F(y) = 3.5x
In the first table, where x = 2
y= 3.5 *2
= 7
This iteration goes on and on and is consistent for all the values.
In the second table,
Where F(y) is known, for example 10.5, then x is derived as:
10.5 = 3.5x (divide both sides by 3.5)
x = 3
This iteration goes on and on and is consistent for all the values.
In the third table, we simply swap the values back and forth using the function F(y) = 3.5x to derive all values.
Learn more about graphs:
https://brainly.com/question/16608196
#SPJ1
Which is the graph of linear inequality 2y > x-2?

Answers
Answer:
top line third option with shaded above.
Step-by-step explanation:
it's the third option because it's a
dotted line because it's not included (since it doesn't say greater than or equal to). Also, greater than is shaded above the line.
The third graph is the correct representation of the given inequality.
What are linear inequalities?Linear inequalities are defined as a mathematical expression that compares two expressions using the inequality symbol.
The given inequality is 2y > x-2.
i.e y > (x-2)/2
Since the inequality sign does not contain an equals sign, the line is drawn as a dashed line.
The upper region satisfies the inequality.
Hence, the upper shaded portion with the dashed line is the correct graph for the given inequality.
To learn more about linear inequality, use the link given below:
https://brainly.com/question/11897796
#SPJ2
Evaluate the iterated integral by converting to polar coordinates. 20 sqrt(2x − x2) 0 6 sqrt(x2 + y2) dy dx
Answers
The supplied statement states that the iterated integral after being converted to interpolation is 32/3.
What is the definition of an integral?In mathematics, an integral is either a number representing the region beneath a function's graph over a certain interval or just a new function, the reverse of which contains the original mechanism (indefinite integral). To complete the whole, an essential component is required. The term "essential" is almost a synonym in this context. Trigonometric functions of functional and equations are a concept in mathematics. Integral is a derivative of Middle English, Latin integer, and Medieval Latin integralis, each of which mean "making up a whole."
Therefore, the area is,
\(R=\left\{(x, y) \mid 0 \leq x \leq 2,0 \leq y \leq \sqrt{2 x-x^2}\right\}\)
So,
\(y=\sqrt{2 x-x^2}\)
y² = 2x - x²
x² - 2x + y² = 0
x² - 2x + 1 + y² = 1
(x-1)² + y² = 1
In other words, the area is the middle section of the disk with a radius of 1 and a center at (0,1).
Region R's polar coordinates are
x = r cos∅, y = r sin∅
So,
\(y=\sqrt{2 x-x^2}\)
y² = 2x - x²
x² + y² = 2x
r² = 2r cos∅
r = 2 cos∅
The polar coordinates of the sphere of integration as,
\(R=\left\{(r, \theta) \mid 0 \leq \theta \leq \frac{\pi}{2}, 0 \leq r \leq 2 \cos \theta\right\}\)
The provided integral then becomes,
\(\begin{aligned}& \int_0^2 \int_0^{\sqrt{2 x-x^2}} 6 \sqrt{x^2+y^2} d y d x \\= & \int_0^{\frac{\pi}{2}} \int_0^{2 \cos \theta} 6 r \cdot r d r d \theta \\= & \int_0^{\frac{\pi}{2}} \int_0^{2 \cos \theta} 6 r^2 d r d \theta \\= & \int_0^{\frac{\pi}{2}} 6\left(\frac{r^3}{3}\right)_0^{2 \cos \theta} d \theta\end{aligned}\)
\(\begin{aligned}& =\int_0^{\frac{\pi}{2}} 2\left(8 \cos ^3 \theta-0\right) d \theta \\& =16 \int_0^{\frac{\pi}{2}} \cos ^2 \theta \cdot \cos \theta d \theta \\& =16 \int_0^{\frac{\pi}{2}}\left(1-\sin ^2 \theta\right) \cdot \cos \theta d \theta\end{aligned}\)
Let u = sin∅ then du = cos ∅ d∅
If ∅ = 0 then u = 0 and if ∅ = π/2 then u = 1.
The above integral thus becomes,
\(\begin{aligned}& \int_0^2 \int_0^{\sqrt{2 x-x^2}} 6 \sqrt{x^2+y^2} d y d x \\= & 16 \int_0^1\left(1-u^2\right) d u \\= & 16\left(u-\frac{u^3}{3}\right)_0^1 \\= & 16\left(1-\frac{1}{3}\right)\end{aligned}\)
= 32/3
To know more about Integral visit:
https://brainly.com/question/22008756
#SPJ4
Two sides of a triangle are 4m and 5m in length and the angle between them is angle. write the formula for the area of the triangle as a function of angle
Answers
The rate at which the area of the triangle is increasing when the angle between the sides of fixed lengths is π/3 is 0.3 m²/s.
What is the rate of change of an area?If the lengths a and b for two sides of the triangle, as well as the included angle θ, are known, the area of a triangle can be calculated using the sine formula.
\(\text { Area }=\frac{1}{2} a b \sin \theta\)
Now, according to the question;
The two sides of the triangle are given;
Let a = 4m and b = 5m.
Let θ = π/3. be the angle between the two sides;
Then,
Differentiate the area with respect to time (as rate of change of area)
\(\begin{aligned}\frac{\mathrm{d} A}{\mathrm{~d} t}=\frac{\mathrm{d}}{\mathrm{d} t} \frac{1}{2} a b \sin \theta &=\frac{1}{2} * 4 * 5 * \frac{\mathrm{d}(\sin \theta)}{\mathrm{d} \theta} \cdot \frac{\mathrm{d} \theta}{\mathrm{d} t} \\&=10 *(\cos \theta) * 0.06 \frac{\mathrm{m}^{2}}{\mathrm{~s}}=0.6 \cos (\pi / 3) \frac{\mathrm{m}^{2}}{\mathrm{~s}} \\&=0.6 * 0.5 \frac{\mathrm{m}^{2}}{\mathrm{~s}}=0.3 \frac{\mathrm{m}^{2}}{\mathrm{~s}}\end{aligned}\)
Therefore, the area of the triangle as a function of angle is 0.3 m²/s.
To know more about rate of change of area, here
https://brainly.com/question/17203328
#SPJ4
The complete question is-
Two sides of a triangle are 4m and 5 m in length and the angle between them is increasing at a rate of 0.06 rad/sec. Find the rate at which the area of the triangle is increasing when the angle between the sides of fixed lengths is π/3.
Question 15 (1 point)
If (-3,1) is in the function f(x), then which of the following
points will be in the function f-'(x)?
(1, -3)
(3,-1)
(-1,3)
(-1,-3)
Answers
The point which will be in function is f-'(x) is (1, -3).
We are given that;
The point (-3,1) is in the function f(x)
Now,
Function is a type of relation, or rule, that maps one input to specific single output.
A function is an expression, rule, or law that describes the relationship between one variable (the independent variable) and another variable (the dependent variable) (the dependent variable). In mathematics and the physical sciences, functions are indispensable for formulating physical relationships.
Linear function is a function whose graph is a straight line
To find the inverse of a function, we need to switch the inputs and outputs of the function.
In other words, if f(x) = y, then f^ {-1} (y) = x.
This means that if (-3, 1) is in the function f(x), then (1, -3) will be in the function f^ {-1} (x).
Therefore, by function answer will be (1, -3).
Learn more about function here:
https://brainly.com/question/2253924
#SPJ2
The absolute value of a positive or negative number is always going to be greater than or equal to 0. a) absolute value equation b) inverse operations c) linear equation d) property of absolute value
Answers
the absolute value of a positive or negative number is always greater than or equal to 0, which is a property of absolute value.
The given statement is related to the property of absolute value.
The main answer to the question is that the absolute value of a positive or negative number is always greater than or equal to 0.
The absolute value of a number represents its distance from 0 on a number line, regardless of whether the number is positive or negative. Since distance cannot be negative, the absolute value is always non-negative or greater than or equal to 0.
the absolute value of a positive or negative number is always greater than or equal to 0, which is a property of absolute value.
To know more about absolute value visit:
https://brainly.com/question/17360689
#SPJ11
Four friends all five each other presents
The total cost of presents is £80.52
Work out the mean cost of presents in pounds
Answers
Step-by-step explanation:
Four friends all give each other presents. The total cost of the presents is £80.52. We need to find the mean cost of a present in pounds. So, the mean cost of a present is equal to 20.13 .