A flagpole is 25 ft tall. The flagpole is casting a shadow that is 42 feetlong. What is the angle of depression?

Answers
We can draw the following picture:
then we need to find angle theta. However, in order to find theta, we must find angle x first.
Since we have a right triangle, we can apply the tangent function as:
\(\tan x=\frac{42}{25}\)then, x is given by
\(\begin{gathered} x=\tan ^{-1}(\frac{42}{25}) \\ x=\tan ^{-1}(1.68) \end{gathered}\)then, x is equal to
\(x=59.24\text{ degr}ees\)Now, angle x and angle theta are complementary, this means that
\(x+\theta=90\)then, we have
\(\begin{gathered} \theta=90-x \\ \theta=90-59.24 \\ \theta=30.76 \end{gathered}\)Therefore, the angle of depression (theta) is equal to 30.76 degrees.

Related Questions
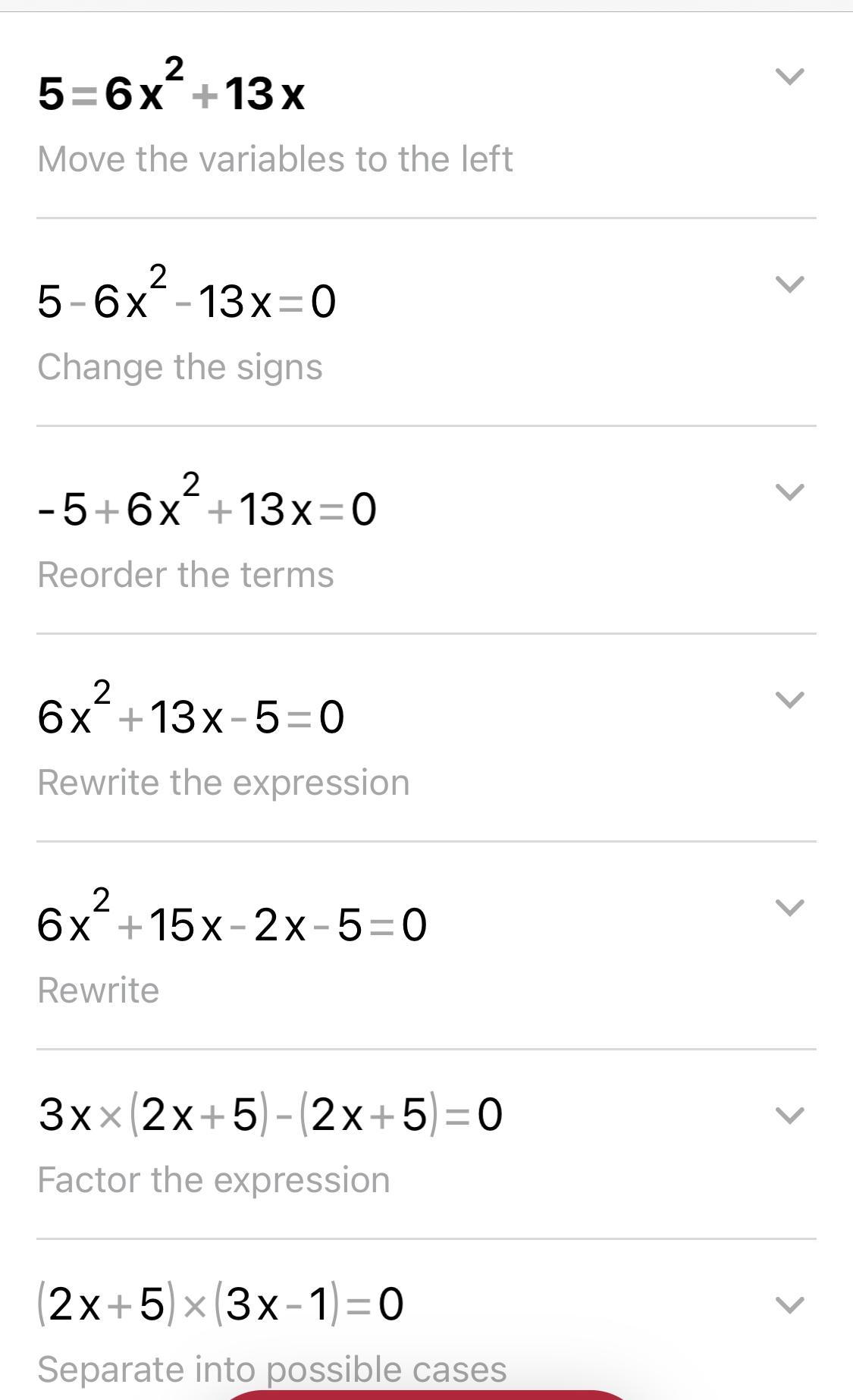
Solve using the quadratic formula or factoring ... 5=6x^2 + 13x
Answers
Answer:
x = \(\frac{-5}{2}\) or x = \(\frac{-1}{3}\)
Step-by-step explanation:
5 − 6 2 − 1 3 = 0
− 6 2 − 1 3 + 5 = 0 -6x^2-13x+5=0 −6x2−13x+5=0 − 1
( 6 2 + 1 3 − 5 ) = 0
Answer:
- 5/2, 1/3
Step-by-step explanation:
See image below:) I could only show half of the steps. But you can use the app photo math you just take a pic of the problem and it gives you the answer and explains the steps.
5a. find the value of a.

Answers
The logarithmic function f(x) = a·log₃(x - 4), passing through the points (13, 7), has the values;
5 a. The value of a is 3.5
b. Please find attached the graph of the function, f(x) = 3.5·log₃(x - 4), created with MS Excel
What is a logarithmic function?A logarithmic function is a function that contain and involves logarithm operation and it is the inverse of an exponential function
The function is f(x) = a·log₃(x - 4),
x > 4 and a > 0
The coordinates of a point on the graph of the function, f is A(13, 7)
5 a. The value of a can be found by plugging in the value of (13, 7) = (x, f(x)), as follows
f(13) = 7 = a·log₃(13 - 4) = a·log₃9 = a·log₃3²
7 = a·log₃3²
7 = 2·a·log₃3 = 2·a·1 = 2·a
2·a = 7
a = 7 ÷ 2 = 3.5
a = 3.5
5 b. The coordinates of the x-intercept of the graph = (5, 0)
The equation of the function is;
f(x) = 3.5·log₃(x - 4)
A third point on the graph is given when f(x) = 14 as follows;
f(x) = 14 = 3.5·log₃(x - 4)
log₃(x - 4) = 14 ÷ 3.5 = 4
3⁴ = x - 4
x = 3⁴ + 4 = 85
Which gives the point, (85, 14)
Similarly, we have the point (31, 10.5), (7, 3.5)
Please find attached the graph of f(x) created with MS Excel
Learn more about logarithmic functions here:
https://brainly.com/question/28033379
#SPJ1

How many feet are there in 3 meters?
Hint: 1 m 3.3 ft
Round your answer to the nearest tenth.
Answers
Answer:
9.8
Step-by-step explanation:
Answer:
9.9
Step-by-step explanation:
2. The diagram above shows a wooden structure in the form of a cone mounted on hemispherical base. The vertical height of the cone is 24cm and the base 7cm. Calculate correct to 3 significant figures the surface area of the structure. (Take π= 22/7)
Answers
The surface area of the wooden structure is approximately 1012 cm².
To calculate the surface area of the wooden structure, we need to find the surface area of the cone and the surface area of the hemispherical base, and then add them together.
Surface Area of the Cone:
The surface area of a cone is given by the formula:
A_{cone = \(\pi \times r_{cone} \times (r_{cone} + s_{cone})\), \(r_{cone\) is the radius of the base of the cone and \(s_{cone\) is the slant height of the cone.
The vertical height of the cone is 24 cm, and the base radius is 7 cm, we can calculate the slant height using the Pythagorean theorem:
\(s_{cone\) = \(\sqrt{(r_{cone}^2 + h_{cone}^2).\)
Using the given measurements:
\(s_{cone\) = √(7² + 24²) cm
\(s_{cone\) ≈ √(49 + 576) cm
\(s_{cone\) ≈ √625 cm
\(s_{cone\) ≈ 25 cm
Now, we can calculate the surface area of the cone:
\(A_{cone\) = π × 7 cm × (7 cm + 25 cm)
\(A_{cone\) = (22/7) × 7 cm × 32 cm
\(A_{cone\) = 704 cm²
Surface Area of the Hemispherical Base:
The surface area of a hemisphere is given by the formula:
\(A_{hemisphere\) = \(2 \times \pi \times r_{base}^2\), \(r_{base\) is the radius of the base of the hemisphere.
Given that the base radius is 7 cm, we can calculate the surface area of the hemispherical base:
\(A_{hemisphere\) = 2 × (22/7) × (7 cm)²
\(A_{hemisphere\) = (22/7) × 2 × 49 cm²
\(A_{hemisphere\) = 308 cm²
Total Surface Area:
To calculate the total surface area, we add the surface area of the cone and the surface area of the hemispherical base:
Total Surface Area = \(A_{cone} + A_{hemisphere}\)
Total Surface Area = 704 cm² + 308 cm²
Total Surface Area = 1012 cm²
For similar questions on surface area
https://brainly.com/question/16519513
#SPJ8
Can someone help !!
2. What is the probability that you select a Jack given that it is a Club?
P(Jack∣Club)=
3. What is the probability that you select a Club given that it is a Jack?
P(Club∣Jack)=
4. What is the probability that you select a card that is NOT a Jack given that it is NOT a Club?
P(NotJack∣NotClub)=
5. What is the probability that you select a card that is NOT a Club given that is it NOT a Jack?

Answers
The probability that you select a Jack given that it is a Club P(Jack∣Club) is 1/13.
The probability that you select a Club given that it is a Jack is P(Club∣Jack) is 1/4.
The probability that you select a card that is NOT a Jack given that it is NOT a Club,P(NotJack∣NotClub) is 47/38
The probability that you select a card that is NOT a Club given that is it NOT a Jack is 38/47
The probability that you select a Jack given that it is a Club P(Jack|Club):
There are 4 Jacks in a deck (one for each suit), and since we are given that the selected card is a Club, we only need to consider the 13 cards in the Club suit.
So, the number of favorable outcomes is 1 (the Jack of Clubs), and the total number of possible outcomes is 13 (the number of cards in the Club suit)
P(Jack|Club) = 1 / 13
The probability that you select a Club given that it is a Jack
P(Club|Jack):
P(Club|Jack) = Number of favorable outcomes / Total number of possible outcomes
P(Club|Jack) = 1 / 4
The probability that you select a card that is not a Jack given that it is not a Club
P(NotJack|NotClub):
The number of cards that are not Jacks is 52 - 4 = 48 (since there are 4 Jacks in the deck), and the number of cards that are not Clubs is 52 - 13 = 39 (since there are 13 cards in the Club suit).
P(NotJack|NotClub) = Number of favorable outcomes / Total number of possible outcomes
P(NotJack|NotClub) = (48 - 1) / (39 - 1)
=47/38
P(NotClub|NotJack) = (39 - 1) / (48 - 1)
=38/47
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ1
Which is the answer??????????

Answers
Answer:
(B) v=p-10 1/10
Step-by-step explanation:
v does equal p if you take 10.1 away each time that's what the 1/10 is there for
Game stop buys a game for $28 and marks the game up 64%. How much will you pay for the game?
Explain it and answer it please.
Answers
you would multiply 28 by the 64% (0.64). when you multiply, you should get $17.92. you take that price and subtract from the initial amount ($28), & you should get the final price which is $10.08 .
Drag each tile to the correct box. Graph the functions as transformations of f(x)=x^2. Arrange the parabolas with respect to the position of their vertices from left to right. 1: y=f(x)
2: y=f(x-4)
3: y=f(x+3)
4: y=f(x-7)
5: y=f(x+2)
6:y=f(x-1/2)
Answers
If a constant is added to a variable then the graph gets shifted toward left and vice-versa. Then the graphs are shown below.
What is the parabola?It's the locus of a moving point that keeps the same distance between a stationary point and a specified line. The focus is a non-movable point, while the directrix is a non-movable line.
The parabola is given below.
f(x) = x²
Then the parabolas with respect to the position of their vertices from left to right will be
1: y = f(x) = x²
2: y = f(x - 4) = (x - 4)²
3: y = f(x + 3) = (x + 3)²
4: y = f(x - 7) = (x - 7)²
5: y = f(x + 2) = (x + 2)²
6: y = f(x - 1/2) = (x - 1/2)²
The graph of the parabola is given below.
More about the parabola link is given below.
https://brainly.com/question/8495504
#SPJ1

what would you do with a TV if you are from the past and dont know to do with it
Answers
Answer:
lol I would think its some type of witchcraft. probably burn it!
In a lottery game, a player picks six numbers from 1 to 25. If the player matches all six numbers, they win 40,000 dollars. Otherwise, they lose $1.
What is the expected value of this game? $
Answers
Answer: around -$0.77
Step-by-step explanation:
To calculate the expected value of this lottery game, we need to find the probability of winning the game and the probability of losing the game.
Probability of winning:
There are a total of C(25, 6) possible combinations of choosing 6 numbers out of 25, where C(n, k) represents the number of combinations of choosing k items from a set of n items. The formula for combinations is:
C(n, k) = n! / (k!(n-k)!)
C(25, 6) = 25! / (6!19!) = 177100
So, there are 177,100 possible combinations. Since there's only 1 winning combination, the probability of winning is:
P(Winning) = 1 / 177,100
Probability of losing:
Since there's only 1 winning combination, the probability of losing is:
P(Losing) = 1 - P(Winning) = 1 - (1 / 177,100) = 177,099 / 177,100
Expected value:
Now, we can calculate the expected value (EV) by multiplying the probabilities of each outcome by their respective values and then summing up these products:
EV = P(Winning) * Value(Winning) + P(Losing) * Value(Losing)
EV = (1 / 177,100) * $40,000 + (177,099 / 177,100) * (-$1)
EV ≈ ($40,000 / 177,100) - ($177,099 / 177,100)
EV ≈ $0.2256 - $1
EV ≈ -$0.7744
The expected value of this lottery game is approximately -$0.7744. This means that, on average, a player would lose about 77.44 cents per game.
Activity
Blaine is selling tickets to a rock concert. Tickets in the front section cost $60 each. Tickets in the back section cost $40
each. Blaine has 55 tickets left to sell, and to meet his sales quota he needs to sell more than $600 in tickets from the
remaining tickets.
Blaine makes a profit of $40 on every ticket for the front section. He makes a profit of $25 on every ticket for the back
section. What's the maximum profit Blaine can make from selling his remaining tickets?
You may find it helpful to review the steps of linear programming e.
Part A
Write the system of inequalities for the given situation where x represents the number of front section tickets and y
represents the number of back section tickets.
Answers
Answer:
25 tickets more
Step-by-step explanation:
I got x+y is (less than or equal to) 55 for the first inequality and 60x+40y>600 for the second one!
Step-by-step explanation:
Since Blaine can sell a maximum of 55 tickets, the first inequalitly is x+y is less than OR EQUAL TO 55. Since the tickets in the back section cost $40 each, 40y represents the money made from those tickets. Blaine needs to make 600 in sale so the inequality is 60x+40y>600.
Which expression shows the distance on the number line between 2 and -7? O 02-(-7) 0 12 - 7 0 1 7+2 O 12+(-7)

Answers
Answer:
=∣∣−5∣∣=5
Step-by-step explanation:
∣∣x−y∣∣=5
Solution:
∣∣x−y∣∣
=∣∣2−7∣∣
=∣∣−5∣∣=5
Answer:
l2-7l
Step-by-step explanation:
Question 1 Part A:
Select and use the most direct method to solve
3x(x - 3) = 12
X=___ Or X=____
Answers
The solution of the equation 3x(x - 3) = 12 will be 4 and negative 1.
What is the solution to the equation?The allocation of weights to the important variables that produce the calculation's optimum is referred to as a direct consequence.
The definition of simplicity is making something simpler to achieve or grasp while also making it a little less difficult.
The equation is given below.
3x(x - 3) = 12
Simplify the equation, then we have
3x(x - 3) = 12
x(x - 3) = 4
x² - 3x - 4 = 0
Factorize the equation, then we have
x² - 3x - 4 = 0
x² - 4x + x - 4 = 0
x(x - 4) + 1(x - 4) = 0
(x - 4)(x + 1) = 0
x = 4, -1
The solution of the equation 3x(x - 3) = 12 will be 4 and negative 1.
More about the solution of the equation link is given below.
https://brainly.com/question/545403
#SPJ1
A lorry left town A to town B and maintained an average speed of 50km/hr. A car left town A for town B 42 minutes later maintained an average speed of 80km/hr . At the time car arrived to town B the lorry had 25km to cover to town B. Determine the distance between town A and B
Answers
The distance between town A and town B is 93.5 km.
Solving for the distance between town A and town B:
Let's first convert the 42 minutes delay of the car to hours:
42 minutes = 42/60 hours
= 0.7 hours
Now, let's assume that the time it took for the car to travel from A to B is t hours.
The distance between A and B is the same for both the lorry and the car, so we can set up an equation:
Distance = Speed x Time
For the lorry:
Distance = 50t
For the car:
Distance = 80 (t-0.7)
We know that when the car arrived at B, the lorry had 25km left to cover. So:
50t - Distance covered by lorry = 25
50t - (50t - 25) = 25
Simplifying:
25 = 25
This equation is always true, which means our assumptions are correct.
Therefore, we can equate the two distance equations:
50t = 80(t-0.7)
50t = 80t - 56
30t = 56
t = 1.87 hours
Finally, we can use the distance equation with either the lorry or the car to find the distance between A and B:
Distance = Speed x Time
Distance = 50 x 1.87
Distance = 93.5 km
So the distance between town A and town B is 93.5 km.
Learn more about distance on
https://brainly.com/question/15172156
#SPJ1
Find (−2)(−8). please.
Answers
Answer:
16
Step-by-step explanation:
How do you solve this 18(6-c)+13c=123
Answers
Answer:
\(c = -3\)
Step-by-step explanation:
Isolate the variable by dividing each side by factors that don't contain the variable.
Newsweek performed a poll in which 500 American parents were asked the question, “Would you prefer to have your child taught by a male or female for grades K-2?” Only 40% responded that they would prefer to have their child taught by a male in grades K-2. Construct a 95% confidence interval for the poll.
Answers
The 95% confidence interval for the poll is given as follows:
(0.3571, 0.4429).
What is a confidence interval of proportions?A confidence interval of proportions has the bounds given by the rule presented as follows:
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which the variables used to calculated these bounds are listed as follows:
\(\pi\) is the sample proportion, which is also the estimate of the parameter.z is the critical value.n is the sample size.The confidence level is of 95%, hence the critical value z is the value of Z that has a p-value of \(\frac{1+0.95}{2} = 0.975\), so the critical value is z = 1.96.
The sample proportion and the estimate for this problem are given as follows:
\(\pi = 0.4, n = 500\)
Then the lower bound of the interval is calculated as follows:
\(\pi - z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.4 - 1.96\sqrt{\frac{0.4(0.6)}{500}} = 0.3571\)
The upper bound of the interval is calculated as follows:
\(\pi + z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.4 + 1.96\sqrt{\frac{0.4(0.6)}{500}} = 0.4429\)
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
if two angles at the base of an isosceles triangle are 50, the other angle is _____because_____________________________________________.
please helpp
Answers
Explanation: So if the 2 base angles have a sum of 50 then the third angle is 180-50=130
The pair of points (g, -1) and (2, 5) lie on a line with a slope of 3/2. What is the value of g?
3
-2
-5
4
Answers
The variable g has its value to be -4 on the given coordinate point
How to calculate the value of point G of the line?From the question, the points are given as
(g, -1) and (2, 5)
Rewrite the above points properly
So, we have the following ordered pairs
(x, y) = (g, -1) and (2, 5)
The slope of the line is given as
Slope = 3/2
The slope of the line is then calculated using the following slope equation
Slope = (y₂ - y₁)/(x₂ - x₁)
Where
(x, y) = (g, -1) and (2, 5)
Substitute the known values in the above equation
So, we have the following equation
3/2 = (5 + 1)/(2 - g)
Evaluate the sum in the equation
This gives
3/2 = 6/2 - g
Cross multiply
So, we have
2(2 - g) = 12
Divide by 2
2 - g = 6
Make g the subject of the formula
g = 2 - 6
Evaluate the like terms
g = -4
Hence, the value of g of the line is -4
Read more about slope at
brainly.com/question/3493733
#SPJ1
Answer:
-2
Step-by-step explanation:
Write an expression using the distributed property to dind the product of 7x63
Answers
The product of the expression 7 x 63 is 441.
We have,
To find the product of 7 x 63 using the distributive property, we can break down 63 as the sum of its factors, such as 60 and 3:
7 x 63 = 7 x (60 + 3)
Now, we can apply the distributive property by multiplying 7 to each term inside the parentheses:
7 x (60 + 3) = 7 x 60 + 7 x 3
Simplifying further:
7 x 60 + 7 x 3 = 420 + 21
Therefore,
The product of 7 x 63 is 441.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
Select all the points that lie on the graph of the line 3x-8y=14.(-26,8)(-6,-4)(10,2)(18,5)(22,-10)
Answers
One way to answer this is by plugging each point for x and y in the equation as follows:
Then:
For (-26, 8), we have:
3 * (-26) - 8 * (8) = -142 (No).
For (-6, -4), we have:
3 * (-6) - 8 * (-4) = 14 (Yes).
For (10, 2), we have:
3 * (10) - 8 * (2) = 14 (Yes).
For (18, 5), we have:
3 * (18) - 8 * (5) = 14 (Yes).
For (22, -10), we have:
3 * (22) - 8 * (-10) = 146 (No).
Then, the points that lie on the graph of the line 3x - 8y = 14 are: (-6, -4), (10, 2), and (18, 5).
write an equation in point-slope form of the line that passes through the point (3, 5) and has a slope or -1
Answers
Answer:
y = -x + 8
Step-by-step explanation:
m = -1 ; x1 = 3 ; y1 = 5
Slope point form: y - y1 = m(x -x1)
y - 5 = -1(x - 3)
y - 5 = -1x - 3 *(-1)
y - 5 =-x + 3
y = -x + 3 + 5
y = -x + 8
Mark bought 114 meters of fencing to enclose an area of pasture for his sheep.he plans to use all of the fencing to make a rectangle that is twice as long as it is wide.
Question/ Find the length (in meters ) of the area he plans the fence in
Answers
Answer:
38 meters
Step-by-step explanation:
Determine the equation of the parabola that opens to the right, has focus (13,-6),
and a focal diameter of 28.
Answers
The equation of the parabola is\((y + 6)^2 = 4(x - 13)\), where the vertex is (13, -6) and the distance between the directrix and focus is 14.
To determine the equation of the parabola, we need to use the standard form for a parabola with a horizontal axis:
\((x - h)^2 = 4p(y - k)\)
Where (h, k) represents the vertex of the parabola, and p is the distance from the vertex to the focus (and also from the vertex to the directrix).
Given that the parabola opens to the right, the vertex will be on the left side. Let's assume the vertex is (h, k).
We know that the focus of the parabola is at (13, -6), so the distance from the vertex to the focus is p = 13 - h.
We are also given that the focal diameter is 28, which means the distance between the directrix and the focus is twice the distance from the vertex to the focus.
Therefore, the distance from the vertex to the directrix is d = 28/2 = 14.
for such more question on parabola
https://brainly.com/question/18274774
#SPJ11
Which statement about function g is true?
g(x)
10
x
1
2 40
3 160
4 640

Answers
The statement about function g which is true is that: function g is exponential because g(x) changes by equal factors over equal intervals of x.
What is a slope?The slope of a line simply refers to the gradient of a line and it's typically used to describe both the ratio, direction and steepness of an equation of a straight line.
How to calculate the slope of a line?Mathematically, the slope of a straight line can be calculated by using this formula;
\(Slope = \frac{Change\;in\;y\;axis}{Change\;in\;x\;axis}\\\\Slope = \frac{y_2\;-\;y_1}{x_2\;-\;x_1}\)
Slope = (40 - 10)/(2 - 1)
Slope = 30/1
Slope = 30
Slope = (160 - 40)/(3 - 2)
Slope = 120/1
Slope = 120.
Factor = 40/10 = 4
Factor = 160/40 = 4
Factor = 640/160 = 4.
Therefore, function g is exponential because g(x) changes by equal factors over equal intervals of x.
Read more on slope here: https://brainly.com/question/18028474
#SPJ1
Which of the following numbers is the
smallest?
A 73
B 7.45
C 7.75
D 7
E 72
Answers
foreign direct investment helps improve the economic situation of a recipient country by increasing —- opportunities in the country that the company invests in.
Answers
Foreign direct investment helps improve the economic situation of a recipient country by increasing employment opportunities in the country that the company invests in.
When foreign companies invest in a recipient country, they often establish or expand their operations, which requires hiring local workers. This leads to job creation and reduces unemployment rates in the recipient country.
Increased employment opportunities result in more individuals having access to income and improved standards of living.
Foreign direct investment also contributes to the transfer of technology, knowledge, and skills to the recipient country. Multinational companies often bring advanced technologies, production techniques, and management practices that may not have been available or widely adopted in the recipient country.
Furthermore, foreign direct investment stimulates domestic investment and encourages the growth of local businesses. When foreign companies invest in a recipient country, they often form partnerships or engage in supply chain relationships with local firms.
Overall, foreign direct investment increases employment opportunities, fosters technology transfer, and stimulates domestic investment, all of which contribute to improving the economic situation of a recipient country.
for similar questions on company invests.
https://brainly.com/question/27717275
#SPJ8
SOMEONE PLSSS HELP MEE AND PLEASE DONT JUST TYPE FOR FUN ALSO ILL GIVE BRAINLESS TO WHOEVERS RIGHT
Solve. −3 2/3=x−1 1/4 What is the solution to the equation? Enter your answer as a simplified mixed number in the box.
Question
Solve.
x−(−2 7/8)=−1/2
What is the solution to the equation?
Enter your answer as a simplified mixed number in the box.
Question
Solve.
−2 1/3x=−1 3/4
What is the solution to the equation?
Enter your answer as a simplified fraction in the box.
Answers
Answer:x-(2 7/8)=1/2
Step-by-step explanation:
JKLM is a triangle. Find the measure of angle KL and JM

Answers
Answer:
x = 10
m∠K = 90°
y = 15
JM = 65
Step-by-step explanation:
KJ = LM
⇒ x + 31 = 5x - 9
⇒ 40 = 4x
⇒ x = 10
From inspection of the diagram, m∠K = 90° (right angle)
KL = JM
⇒ 4y + 5 = 2y + 35
⇒ 2y = 30
⇒ y = 15
JM = 2y + 35
⇒ JM = 2(15) + 35
⇒ JM = 30 + 35
⇒ JM = 65
Opposite sides of rectangle are equal
\(\\ \rm\Rrightarrow x+31=5x-9\)
\(\\ \rm\Rrightarrow 4x=40\)
\(\\ \rm\Rrightarrow x=10\)
m<K=90°\(\\ \rm\Rrightarrow 4y+5=2y+35\)
\(\\ \rm\Rrightarrow 2y=30\)
\(\\ \rm\Rrightarrow y=15\)
KL=JM=2(15)+35=30+35=652x+2y=16x Solve for X Solve for Y
Answers
Answer:
x = \(\frac{y}{7}\), y = 7x
Step-by-step explanation:
hope this helps