a farmer hires 110 workers to harvest apples from his trees .it's takes the 12 days to harvest the farmers entire crop .how long will it take 440farmes to harvest the crop
Answers
110 = 12
12 × 4 = 48 days
hope I'm right
Related Questions
Condense each Logarithm

Answers
The equation of logarithm are solved and
a) A = 2 + 3 log x + 4 log b
b) B = ( 36 + x + y ) ( log 6 )
c) C = ( 1/2 )x log 5
d) D = ln ( x⁴ / y² )
Given data ,
Let the logarithmic equation be represented as A
Now , the value of A is
a)
A = 2 log 10 + 3 log x + 4 log b
The base of the logarithm is 10 , so
A = 2 + 3 log x + 4 log b
b)
B = log 6³⁶ + log 6ˣ - log 6^ ( y )
From the properties of logarithm , we get
log A + log B = log AB
log A − log B = log A/B
log Aⁿ = n log A
B = 36 log 6 + x log 6 + y log 6
On taking the common term , we get
B = ( 36 + x + y ) ( log 6 )
c)
C = ( 1/2 )log 5ˣ
From the properties of logarithm , we get
C = ( 1/2 )x log 5
d)
D = 4 ln x - 2 ln y
From the properties of logarithm , we get
D = ln x⁴ - ln y²
On further simplification , we get
D = ln ( x⁴ / y² )
Hence , the logarithmic equations are solved
To learn more about logarithm click :
https://brainly.com/question/12049968
#SPJ1
The formula d=rt is used to calculate the distance
an object travels over a period of time, t, at a
constant rate, r. Based on this formula, what is the
rate, r, in terms of d and t?
A) r = d/t
B)r = dt
C)r = t/d
D) r = r - t
Answers
Raphael purchased a 3-year-old car for $16,000. He was told that this make and model
depreciates exponentially at a rate of 5.45% per year. What was the original price of the car
when it was new?
Answers
Answer:
$18,760.76
Step-by-step explanation:
16000 * 0.0545 = 872
16000 + 872 = 16872
16872 * 0.0545 = 919.52
16872 + 919.52 = 17791.52
17791.52 * 0.0545 = 969.64
17791.52 + 969.64 = 18760.76
hope this helps. if you need more help lmk. Happy Holidays!
Answer:$18,929.34
Step-by-step explanation: This is the correct answer.
Angle ADB and CD are straight lines. angle ADC = 5 x angle CDB Work out the size of angle ADC.

Answers
Answer:
Step-by-step explanation:

Help please if you know, thanks

Answers
Answer:
xsqrt(2)
Step-by-step explanation:
sqrt(a) / sqrt(b) = sqrt(a/b)
sqrt(22x^6) / sqrt(11x^4)
sqrt(22x^6/11x^4)
sqrt(2x^2)
We know sqrt(ab) = sqrt(a) sqrt(b)
sqrt(x^2) sqrt(2)
xsqrt(2)
Solve each of the following equations and show how you checked your answers 2y+4y=6-3y
Answers
Answer:
y=2/3
Step-by-step explanation:
2y+4y=6-3y
⇔ 2y+4y+3y=6
⇔ 9y=6
⇔ y=6/9=2/3
The answer is:
y = 2/3
Work/explanation:
For now, I focus on the left side and combine the like terms:
\(\bf{2y+4y=6-3y}\)
\(\bf{6y=6-3y}\)
Add 3y to each side
\(\bf{6y+3y=6}\)
Combine like terms
\(\bf{9y=6}\)
Divide each side by 9
\(\bf{y=\dfrac{6}{9}}\)
\(\bf{y=\dfrac{2}{3}}\)
Hence, the answer is 2/3.
If a fission reaction yields 4.50×10^9 kJ of energy, then how much mass was lost?
1.50×10^−6 kg
5.00×10^−2 kg
5.00×10^−5 kg
1.50×10^−3 kg
Answers
Answer:
(c) 5.00×10^-5 kg
Step-by-step explanation:
The mass and energy are related by Einstein's formula E = mc².
__
Solving for mass in kg, we find it to be ...
m = E/c² . . . . . . . . where E is in joules, and c is in meters/second
m = (4.50×10^12 J)/(3×10^8 m/s)² = 5.00×10^-5 kg
The lost mass was about 5.00×10^-5 kg.
Answer:
5.00×10^−5 kg
Step-by-step explanation:
I took the test and it was correct! PLEASE LIKE and have a wonderful day!

Henrik grew 3 times as many potatoes as Derek grew. Derek managed to grow 49 potatoes. Henrik already had 173 potatoes harvested from his other field. How many potatoes does Henrik have in all?

Answers
Answer: Henrik grew 147 more potatoes than Derek
Step-by-step explanation:
A contractor is building a tower shaped like a tall
rectangular prism. He is told that the dimensions
of the tower must be 50 ft x 80 ft x 250 ft. The
building is to have 20 floors with a 2.5 ft tall
portion between each floor and for the roof. What
is the volume of each floor of the building?
A. 40,000 ft3
B. 49.500 ft
C. 50,000 ft
D. 60,000 ft
Answers
Answer: I put 50,000 ft^3
Step-by-step explanation: You have to multiply 50, 80, 250 then divide by 20 because you’re looking for the floors only and not the roof and floor
What is the asymptote of the graph of f(x)=5x−1?
Answers
The asymptotes of the graph of \(f(x) = \frac{5}{x - 1}\) are as follows:
Vertical: x = 1.Horizontal: y = 0.What are the asymptotes of a function f(x)?The vertical asymptotes are the values of x which are outside the domain, which in a fraction are the zeroes of the denominator.The horizontal asymptote is the value of f(x) as x goes to infinity, as long as this value is different of infinity.In this problem, the function is:
\(f(x) = \frac{5}{x - 1}\)
For the vertical asymptote, we have that:
\(x - 1 = 0 \rightarrow x = 1\).
For the horizontal asymptote, we have that:
\(y = \lim_{x \rightarrow \infty} f(x) = \frac{5}{\infty - 1} = 0\).
More can be learned about asymptotes at https://brainly.com/question/16948935
#SPJ1
Simplify 4(5x + 8) show work please
Answers
Answer:
20x+32
Step-by-step explanation:
4(5x+8)
4*5x + 4*8
20x+32
In a roll of 50 pennies, there are 12 dated 1977. If a penny is drawn at random, what is the probability that it is dated 1977?
Answers
Thus, probability that the one drawn penny is from 1977 dated pennies is 6/25.
Define about the probability:The probability about an occurrence in an experiment is the likelihood that the event will occur. Any event's probability is a number between (including all) "0" and "1".
If an event's probability is represented by P(E), then we get
If and only if the condition E is an impossibility, P(E) = 0.If and just if E is a specific event, then P(E) = 1.Given data:
Total pennies = 50
number of 1977 dated pennies = 12
probability = favourable outcome / total outcome
probability(1977 dated pennies) = number of 1977 dated pennies/ Total pennies
probability(1977 dated pennies) = 12/50
Divide numerator and denominator by 2.
probability(1977 dated pennies) = 6/25
Thus, probability that the one drawn penny is from 1977 dated pennies is 6/25.
Know more about the probability
https://brainly.com/question/13604758
#SPJ1
If two cards are randomly drawn from a deck of ordinary playing cards, one at a time, with replacement, what is the probability of obtaining no aces
Answers
Answer:
144/169
Step-by-step explanation:
There are 52 cards, 4 are aces, so the probability of not getting ace is 48/52, so we square it, or multiply it by itself to get 144/169
There are 2.54 centimeters in 1 inch. There are 100 centimeters in 1 meter. To the nearest inch, how many inches are in 12 meters?
Answers
Answer:
12 meters = 472.441 inches
~Hope this helps~
What is the result when the number 38 is decreased by 50%?
Answers
Answer:
19
Step-by-step explanation:
38 - 50% = 19
What is the area of the kite? 21 square feet 40 square feet 42 square feet 84 square feet.
Answers
Answer:
A=pq2 is the answer i think
evaluate this following questions

Answers
Answer:
Step-by-step explanation:

Answer:
\((i) \quad\;\;\; \left(3^0 + 4^{-1}\right) \times 2^2=5\)
\((ii) \quad \;\;\left(2^{-1} \times 4^{-1}\right) \div 2^{-2}=\dfrac{1}{2}\)
\((iii) \quad \left(\dfrac{1}{2}\right)^{-2}+\left(\dfrac{1}{3}\right)^{-2}+\left(\dfrac{1}{4}\right)^{-2}=29\)
\((iv) \quad \;\: \left(3^{-1}+4^{-1}+5^{-1}\right)^0=1\)
\((v) \quad \;\;\left\{\left(\dfrac{-2}{3}\right)^{-2}\right \}^2=\dfrac{81}{16}\)
Step-by-step explanation:
To evaluate the given expressions, we can use the following exponent rules:
\(\boxed{\begin{minipage}{6cm}\underline{Exponent Rules}\\\\$a^0=1$ \qquad \qquad \qquad \qquad $1^n=1$\\\\\\$a^b \times a^c=a^{b+c}$ \qquad \;\;$a^b \div a^c=a^{b-c}$\\\\\\$\left(\dfrac{a}{b}\right)^c=\dfrac{a^c}{b^c}$ \qquad \qquad $\left(\dfrac{a}{b}\right)^{-c}=\left(\dfrac{b}{a}\right)^{c}$\\\\\\$a^{-n}=\dfrac{1}{a^n}$\qquad \qquad \qquad$\dfrac{1}{a^{-n}}=a^n$\\\\\\$(a^b)^c=a^{bc}$\\\end{minipage}}\)
Part (i)\(\left(3^0 + 4^{-1}\right) \times 2^2\)
\(=\left(1 + (2^2)^{-1}\right) \times 2^2\)
\(=\left(1 + 2^{-2}\right) \times 2^2\)
\(=2^2 + 2^2\times 2^{-2}\)
\(=2^2 + 2^{2-2}\)
\(=2^2 + 2^{0}\)
\(=4+1\)
\(=5\)
Part (ii)\(\left(2^{-1} \times 4^{-1}\right) \div 2^{-2}\)
\(=\left(2^{-1} \times (2^2)^{-1}\right) \div 2^{-2}\)
\(= \left(2^{-1} \times 2^{-2}\right) \div 2^{-2}\)
\(=\left(2^{-1-2}\right) \div 2^{-2}\)
\(=2^{-3} \div 2^{-2}\)
\(=2^{-3-(-2)}\)
\(=2^{-3+2}\)
\(=2^{-1}\)
\(=\dfrac{1}{2^1}\)
\(=\dfrac{1}{2}\)
Part (iii)\(\left(\dfrac{1}{2}\right)^{-2}+\left(\dfrac{1}{3}\right)^{-2}+\left(\dfrac{1}{4}\right)^{-2}\)
\(=\dfrac{1^{-2}}{2^{-2}}+\dfrac{1^{-2}}{3^{-2}}+\dfrac{1^{-2}}{4^{-2}}\)
\(=\dfrac{1}{2^{-2}}+\dfrac{1}{3^{-2}}+\dfrac{1}{4^{-2}}\)
\(=2^2+3^2+4^2\)
\(=4+9+16\)
\(=13+16\)
\(=29\)
Part (iv)\(\left(3^{-1}+4^{-1}+5^{-1}\right)^0\)
\(=1\)
Part (v)\(\left\{\left(\dfrac{-2}{3}\right)^{-2}\right \}^2\)
\(=\left(\dfrac{-2}{3}\right)^{-2\times 2}\)
\(=\left(\dfrac{-2}{3}\right)^{-4}\)
\(=\left(\dfrac{3}{-2}\right)^{4}\)
\(=\dfrac{3^4}{(-2)^4}\)
\(=\dfrac{81}{16}\)
22×(4.5×4.5×4.5+9)=
what is the answer?
Answers
Answer:
2202.75
Step-by-step explanation:
calculator
solve from missing angle

Answers
OQ=4x+2,OQ=4x+2, PQ=4x-10,PQ=4x−10, and OP=3x-3,OP=3x−3, determine the numerical length of OQ
.
Answers
Answer:
22
Step-by-step explanation:
The segment addition theorem tells us the whole is the sum of the parts. We can use this to write an equation relating the expressions for segment length.
SetupOQ = OP +PQ . . . . . segment addition theorem
4x +2 = (3x -3) +(4x -10) . . . . substitute given expressions
Solution15 = 3x . . . . . . add 13 -4x to both sides
5 = x . . . . . . . divide by 3
OQ = 4x +2 = 4(5) +2 = 22
The length of OQ is 22 units.
In a class of 42 students, the number of boys is 2/5 of the girls. Find the number of boys and girls in the class.
Answers
Answer:
BOYS = 30.
GIRLS = 12.
Step-by-step explanation:
Boys: B
Girls: G
B = (2/5)G
B + G = 42.
(2/5)G + G = 42
2G + 5G = 210
7G = 210
G = 210/7
G = 30.
B = (2/5)G
B = (2/5)(30)
B = 60/5
B = 12.
Answer:
\(\Huge \boxed{\bold{\text{12 Boys}}}\)
\(\Huge \boxed{\bold{\text{30 Girls}}}\)
Step-by-step explanation:
Let the number of girls be \(g\) and the number of boys be \(b\).
According to the problem: \(b = \frac{2}{5} \times g\)
We also know that the total number of students is 42, so \(b + g = 42\).
Now, we have two equations with two variables:
\(b = \frac{2}{5} \times g\) \(b + g = 42\)We can solve these equations to find the values of \(b\) and \(g\).
Step 1: Solve for \(\bold{b}\) in terms of \(\bold{g}\)
From the first equation, we have\(b = \frac{2}{5} \times g\)
Step 2: Substitute the expression for \(\bold{b}\) into the second equation
Replace \(b\) in the second equation with the expression we found in step 1.
\(\frac{2}{5} \times g + g = 42\)
Step 3: Solve for \(\bold{g}\)
Now, we have an equation with only one variable, \(g\):
\(\frac{2}{5} \times g + g = 42\)
To solve for \(g\), first find a common denominator for the fractions:
\(\frac{2}{5} \times g + \frac{5}{5} \times g = 42\)
Combine the fractions:
\(\frac{7}{5} \times g = 42\)
Now, multiply both sides of the equation by \(\frac{5}{7}\) to isolate \(g\):
\(g = 42 \times \frac{5}{7}\)\(g = 30\)Step 4: Find the value of \(\bold{b}\)
Now that we have the value of \(g\), we can find the value of \(b\) using the first equation:
\(b = \frac{2}{5} \times g\)\(b = \frac{2}{5} \times 30\)\(b = 12\)So, there are 12 boys and 30 girls in the class.
----------------------------------------------------------------------------------------------------------
The points A, B, and C, shown on the number line, have weights 0.5, 0.3, and 0.2 respectively.
H
в с
2 3 4 5 6 7 8
9 10
Which statement is true about the weighted average, w, of the points A, B, and C?
w lies before A.
w lies beyond C.
w lies between A and B.
w lies between B and C.

Answers
Answer:
"w" (and any subsequent words) was ignored because we limit queries to 32 words.
w = 0.33 so, w lies before A, B, and C.
Option A is the correct answer.
What is a number line?It is the representation of numbers in real order.
The difference between the consecutive numbers in a number line is always positive.
We have,
Average weight.
w = Sum of all the weight / 3
w = (0.5 + 0.3 + 0.2) / 3
w = 1/3
w = 0.33
Now,
A = 3, B = 6, and C = 7 on the number line.
0.33 lies before A, B, C
Thus,
w lies before A.
Learn more about number line here:
https://brainly.com/question/13425491
#SPJ2
brainliest if correct
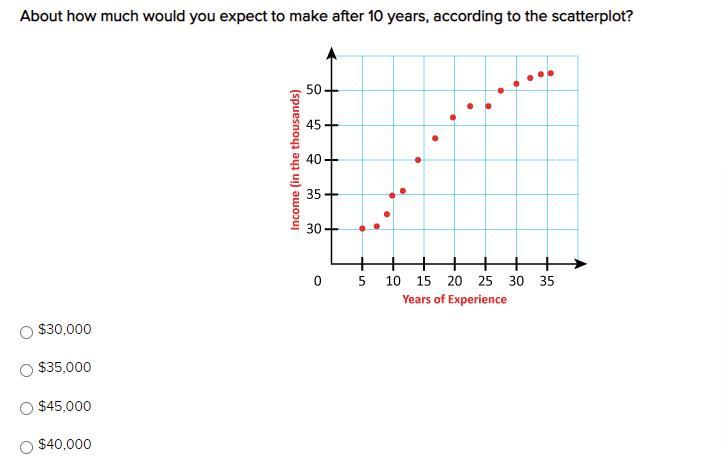
Answers
Answer: $35,000
so The answer is B
hope i helped
Step-by-step explanation:
35,000.
The wage after years experience is shown in this graph. At x = 10, the output is approximately 35k
Hope this helps,
Jeron
:- )
(p.s., maybe brainliest if I really helped?? :)))) )
How can you eliminate the x-terms in this system?

Answers
Answer:
3 times the second equation, plus the first
Step-by-step explanation:
You want a strategy for eliminating x-terms in the system of equations ...
9x -7y = -3-3x +5y = 9EliminationYou can eliminate x-terms by making their coefficients opposites. We observe that the coefficient of x in the first equation is -3 times the coefficient of x in the second equation.
Multiplying the second equation by 3 will make the x-coefficient -9, the opposite of that in the first equation. Doing that makes the system ...
9x -7y = -3-9x +15y = 27Adding these two equations together will eliminate the x-terms:
(9x -7y) +(-9x +15y) = (-3) +(27)
8y = 24 . . . . . . . simplify; x-terms are gone
You can eliminate x-terms by multiplying the second equation by 3, then adding the two equations together.
Identify the correlation you would expect to see between the average amount of snowfall (inches) and the number of school closings.
Answers
Answer:
Simple Linear Regression Correlation
Step-by-step explanation:
When it snows normally the schools continue .But constant snowing affects the schools continuity. As more and more snow falls more schools are closed.
There may be a situation where all the schools are closed at a certain temperature.
So it is a simple linear regression correlation because in it there are two variables and one variable is dependent on the other. In this example the schools are dependent on the average snowfall.
If there's a snow blizzard or extreme weather all the schools are definitely closed .
It can be represented by a graph.

How long do animals live? Beluga whole 40 bengal tiger 10 elephant seal 20 giraffe 25 orangutan 35
Answers
The time period of the animals life cycles are,
⇒ Beluga whole = 35 years
⇒ Bengal tiger = 10 years
⇒ Elephant = 20 years
⇒ Giraffe = 25 years
⇒ Orangutan = 40 years
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
There are some animals and there ages.
Now,
Since, There are some animals and there ages are given.
Hence, The correct ages of the animals are,
⇒ Beluga whole = 35 years
⇒ Bengal tiger = 10 years
⇒ Elephant = 20 years
⇒ Giraffe = 25 years
⇒ Orangutan = 40 years
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
Find the circumstance of a circle with the diameter of 13 meters use 3.14 as an approximation
Answers
Answer:
okay so the circumference is 40.82m
\(circumference = 2\pi \: \times r \\ = 2 \times 3.14 \times 6.5 \\ = 40.82m\)
the diameter will be divided by 2 to give 6.5
The sum of three numbers is 56. The first number is 5 less than the second. The third number is 2 times the second. What are the numbers
Answers
Answer:
10.25, 15.25,30.5
x + (x+5) + 2 (x+5)=56
4× +15=56
x=10.25
Please hurry it’s missing

Answers
exact form 77/8
decimal form 9.625
mixed number form 9 5/8
The function below represents the number of zombies, N, where t is the number of years since the zombies gained control of Earth:
N(t) = 300 · 2-t/8
Is this exponential growth or decay?
Answers
See explanation:
Answer:
This is decay. The exponent has a negative sign. The reciprocal of 2 is 0.5. So N(t) can be rewritten as 0.5^(t/8). The base is fraction less than 1, which is decay.
Step-by-step explanation:
sample response on edgen 2022