(a) Complete this synthetic division table.
-2) 3
-1
-11
8 7
Answers
Answer:
i didnt understand can you plz explain
Related Questions
what would be the slope of (1,-2) and (3,0)
Answers
Answer:
1
Step-by-step explanation:
Hello :)
So to answer this problem, we can use the rise over run formula.
The rise is the difference of any two y values.
The run is the difference of the x values from the same two y values.
This question gives us 1,-2 and 3,0
We can use them for the formula:
-2 - 0 divided by 1 - 3
-2/-2 = 1
Answer:
\(m=1\)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Slope Formula: \(m=\frac{y_2-y_1}{x_2-x_1}\)Step-by-step explanation:
Step 1: Define
Point (1, -2)
Point (3, 0)
Step 2: Find slope m
Substitute [Slope Formula]: \(m=\frac{0+2}{3-1}\)Evaluate Addition/Subtraction: \(m=\frac{2}{2}\)Evaluate Division: \(m=1\)Consider the function f(x)=1/x for x∈R and 35 f(x) =1/5. this is the resonse that need to fix. Start with f(x)=1/x where 3∣ how did we get here? since 30 does it matter that x>0 ? - 1/5 ∗ 1/x ∗
∣x−5∣ I do not follow. Why are we multiplying all of these? - 1/5 ∗ 1/3 ∗
∣x−5∣ where did 1/3 come from? - There for ∣1/x−1/5∣<1/15∣x−5∣ (1) - I do not follow the algebra here. We should have clear steps from ∣f(x)−L∣< epsilon to the delta value. - Then from (1) - We get ∣1/x−1/5∣<1/15∗15 epsion use proper symbols - ∣1/x−1/5∣< Epsilon - Wherever, ∣x−5∣<15 Epsilon - Wherever, for any epsilon >0 we get delta=15epsilon - To get ∣1/x−1/5∣< epsilon, whenever ∣x−5∣<15 epsilon - So, for any ∣1/x−1/5∣< epsilon - Lim x−>5 1/x=1/5 use proper notation with equation editor
Answers
To prove that the limit of 1/x as x approaches 5 is 1/5, we manipulate the expression |1/x - 1/5| < epsilon. By introducing the absolute value of x - 5 and setting |x - 5| < 5 * epsilon, we can choose delta = 5 * epsilon. Therefore, for any epsilon > 0, we have |f(x) - L| < epsilon whenever |x - 5| < delta, confirming that lim(x->5) 1/x = 1/5.
Starting with the function f(x) = 1/x, we want to find a value of delta such that |f(x) - L| < epsilon, where L = 1/5 and epsilon > 0.
To do this, we begin by manipulating the expression |f(x) - L| < epsilon:
|1/x - 1/5| < epsilon
Next, we introduce the absolute value of x - 5:
|1/x - 1/5| = |1/x - 1/5| * |x - 5| / |x - 5|
Here, we multiply both sides of the inequality by |x - 5|, which is positive for x > 0.
Simplifying further:
|1/x - 1/5| * |x - 5| / |x - 5| = |(1 - x/5)/(5x)| * |x - 5|
We notice that 1 - x/5 is less than 1, so we have:
|(1 - x/5)/(5x)| * |x - 5| < |1/(5x)| * |x - 5|
Now, we choose a value for delta such that:
|1/(5x)| * |x - 5| < epsilon
For this to hold, we set |x - 5| < 5 * epsilon, which implies:
|x - 5| < delta = 5 * epsilon
Therefore, for any epsilon > 0, we can choose delta = 5 * epsilon such that |f(x) - L| < epsilon whenever |x - 5| < delta.
In other words, as x approaches 5, the limit of 1/x is indeed 1/5.
Mathematically, we can express this as:
lim(x->5) 1/x = 1/5
To learn more about functions visit : https://brainly.com/question/11624077
#SPJ11
A shape that is can be suggested by dots or dashes that do not connect is known as ___________ shape.Quizlet
Answers
A dotted shape is a type of shape that can be suggested by dots or dashes that don't connect. A shape that can be suggested by dots or dashes that do not connect is known as a Dotted shape.
The term "dotted shape" refers to the shapes that are created by drawing dots or dashes that don't connect. The idea behind this technique is to suggest the shape of an object without drawing its entire outline.The dotted shape technique is commonly used in drawing and graphic design to add a decorative touch to a design. It is also used in children's books and educational materials to teach children about shapes and how to draw them.
There are different types of dotted shapes, including circles, squares, triangles, and rectangles, to name a few. The dotted shape technique can be used to create a variety of designs, from simple to complex, depending on the desired effect.
To know more about shape visit :-
https://brainly.com/question/21335077
#SPJ11
a tank in the shape of a hemisphere has a diameter of 6 feet. if the liquid that fills the tank has a density of 53.3 pounds per cubic foot, what is the total weight of the liquid in the tank, to the nearest full pound?
Answers
The total weight of the liquid in the tank, to the nearest full pound, is calculated to be 3,012 pounds.
The volume of a hemisphere with diameter 6 feet is (2/3) x π x (6/2)³ = 56.55 cubic feet.
The weight of the liquid in the tank can be found by multiplying the volume of the liquid by its density:
Weight = Volume x Density = 56.55 x 53.3 = 3,012.32 pounds.
Rounding this to the nearest full pound gives a total weight of 3,012 pounds. Therefore, the total weight of the liquid in the tank is 3,012 pounds (to the nearest full pound).
Learn more about Hemisphere :
https://brainly.com/question/30480557
#SPJ4
Answer:
3014
Step-by-step explanation:
I just did it
please answer quickly

Answers
1a. 10. 24
1b. 125/243
2a. 0. 0048
2b. 32/3125
3a. 0. 64
3b. 0. 0031
4a. 2/5
4b. 48. 735
5a. 2. 36
5b. 1. 39
How to determine the values
1a. Given the values
(2/5)^2/(1/2)^6
Multiply both the numerator and denominator by the powers
⇒ \(\frac{\frac{4}{25} }{\frac{1}{64} }\)
To find the common ration, multiply thus;
⇒ \(\frac{4}{25}\) × \(\frac{64}{1}\)
⇒ \(\frac{256}{25}\)
= 10. 24
1b. (5/7)^2 × (5/7)^1
= \(\frac{25}{49}\) × \(\frac{5}{7}\)
= \(\frac{125}{343}\)
= 125/243
2a. 0. 6^1 × 0. 2^3
= 0. 6 × 0. 008
= 0. 0048
2b. (2/5)^3 × (2/5)^2
= \(\frac{8}{125}\) × \(\frac{4}{25}\)
= \(\frac{32}{3125}\)
= 32/ 3125
3a. 1^99 - 0. 6^2
= 1 - 0. 36
= 0. 64
3b. (0. 2 ) ^1 × (1/8)^2
= 0. 2 × 1/64
= 0. 2 × 0. 016
= 0. 0031
4a. (1/2)^2/ (5/8)^1
= \(\frac{\frac{1}{4} }{\frac{5}{8} }\)
Take the inverse of the denominator
= \(\frac{1}{4}\) × \(\frac{8}{5}\)
= 2/5
4b. 7^2 - 0. 5^3
= 49 - 0. 125
= 48. 875
5a. 3^1 - 0. 8 ^2
= 3 - 0. 64
= 2. 36
5b. 0. 7^2 + 0. 9^1
= 0. 49 + 0. 9
= 1. 39
Learn more about index notation here:
https://brainly.com/question/10339517
#SPJ1
answer this correctly for brainlist
A family has a unique pattern in their tile flooring on the patio. An image of one of the tiles is shown.
A quadrilateral with a line segment drawn from the bottom vertex and perpendicular to the top that is 5 centimeters. The right vertical side is labeled 3 centimeters. The portion of the top from the left vertex to the perpendicular segment is 5 centimeters. There is a horizontal segment from the left side that intersects the perpendicular vertical line segment and is labeled 6 centimeters.
What is the area of the tile shown?
53 cm2
45.5 cm2
42.5 cm2
36.5 cm2
Answers
Answer:
45.5
Step-by-step explanation:
i passed
i took the test
What is the sum of the three number below ? -16+(-23)+7=
Answers
Answer:
-32
Step-by-step explanation:
What is the value of (−127) − 62 − (−15)?
−174
−50
−204
−80
Answers
Answer:
(-127)-62-(-15)
Open the bracket
-127-62+15
Bodmas rule(addition first)
-127-47=-174
Please answer the circled questions! (also part a b c)

Answers
Answer:
1) Total cost is $27.84
2) a)You first have to divide the product price by their price per pound to find the pound value
2)b) Find their values
2)c) Yolanda bought 3.2 pounds of mixed fruit and 2.8 pounds of dried fruit
3) a) We made a linear equation
3)b) Found the value of x where x is representing the value of pounds
5) She used 6.72 of shampoo
Step-by-step explanation:
1) Total cost = 2.32(3.50)+(2.32)(2)(4.25)
=8.12+(2.32)(2)(4.25)
=8.12+(4.64)(4.25)
=8.12+19.72
=27.84
Total cost is $27.84
2)a) You first have to divide the product price by their price per pound to find the pound value
2)b) find their values
2)c) 21.60/6.75=x
11.90/4.25=y
where, y = value of dried fruit pound value
x= value of mixed fruit value
calculate
Rewrite equations:
3.2=x;2.8=y
Step: Solve3.2=xfor x:
3.2=x
3.2+−x=x+−x(Add -x to both sides)
−x+3.2=0
−x+3.2+−3.2=0+−3.2(Add -3.2 to both sides)
−x=−3.2
−x/−1 = −3.2/−1
(Divide both sides by -1)
x=3.2
Step: Substitute3.2forxin2.8=y:
2.8=y
2.8=y
2.8+−y=y+−y(Add -y to both sides)
−y+2.8=0
−y+2.8+−2.8=0+−2.8(Add -2.8 to both sides)
−y+0=−2.8
−y+0/−1 = −2.8/−1
(Divide both sides by -1)
y+0=2.8
y = 2.8
Yolanda bought 3.2 pounds of mixed fruit and 2.8 pounds of dried fruit
3) a) We made a linear equation
Let's make an equation
3.50x+0.40=20.00
3)b) 3.5x+0.4=20
Step 1: Subtract 0.4 from both sides.
3.5x+0.4−0.4=20−0.4
3.5x=19.6
Step 2: Divide both sides by 3.5.
3.5x/3.5 = 19.6/3.5
x=5.6
Mario bought 5.6 pounds of trail mix
5) 4.8 + 5.4 + 6.6
=10.2+6.6
=16.8
Since she used 2/5 of shampoo we will multiply 2/5 by 16.8
= (16.8)(2)/5
= 33.6/5
=6.72
She used 6.72 of shampoo
Then, substract 6.72 from 16.8
=16.8-6.72
=16.8−6.72
=16.8+−6.72
=10.08
10.08 is the remaining ounces
Therefore, she used 6.72 ounce
Alice and Bob each have a coin. For Alice's coin, the probability of a head is 1/2. For Bob's coin, the probability of a head is 1/3. If each of them tosses their coin once, the probability that they will have different outcomes is
Answers
To find the probability that Alice and Bob will have different outcomes when tossing their coins once, we need to consider the possible combinations of outcomes.
Alice's coin can result in two outcomes: heads (H) with a probability of 1/2 and tails (T) with a probability of 1/2.
Bob's coin can also result in two outcomes: heads (H) with a probability of 1/3 and tails (T) with a probability of 2/3.
The possible combinations of outcomes are:
1. Alice gets H (1/2) and Bob gets T (2/3)
2. Alice gets T (1/2) and Bob gets H (1/3)
The probability that they will have different outcomes is the sum of the probabilities of these two cases.
Probability of different outcomes = (1/2) * (2/3) + (1/2) * (1/3)
= 2/6 + 1/6
= 3/6
= 1/2
Therefore, the probability that Alice and Bob will have different outcomes when tossing their coins once is 1/2 or 50%.
To know more about probability refer here
https://brainly.com/question/31828911#
#SPJ11
to find a power series for the function, centered at 0. f(x) = ln(x6 1)
Answers
The power series for f(x) centered at 0 is:
6 ln(x) + ∑[n=1 to ∞] (-1)^(n+1) / (n x^(6n))
To find a power series for the function f(x) = ln(x^6 + 1), we can use the formula for the Taylor series expansion of the natural logarithm function:
ln(1 + x) = x - x^2/2 + x^3/3 - x^4/4 + ...
We can write f(x) as:
f(x) = ln(x^6 + 1) = 6 ln(x) + ln(1 + (1/x^6))
Now we can substitute u = 1/x^6 into the formula for ln(1 + u):
ln(1 + u) = u - u^2/2 + u^3/3 - ...
So we have:
f(x) = 6 ln(x) + ln(1 + 1/x^6) = 6 ln(x) + 1/x^6 - 1/(2x^12) + 1/(3x^18) - 1/(4x^24) + ...
Thus, the power series for f(x) centered at 0 is:
6 ln(x) + ∑[n=1 to ∞] (-1)^(n+1) / (n x^(6n))
To know more about power series refer here:
https://brainly.com/question/29896893
#SPJ11
Put the following equation of a line into slope-intercept form, simplifying all
fractions.
6x + y = -1
Answers
Answer:
y=6x-1
Step-by-step explanation:
Answer:
\(\bold{-6x + y = -1}\)
Step-by-step explanation:
The slope form is \(y=mx+b\). So, convert this to a slope form:

Which of the following are possible side lengths
for a triangle?
A. 10, 12,3
B. 14, 8,3
C. 15, 5,9
Answers
ANSWER FAST PLEASSEEEEE
The information in the table shows the average weekly temperatures in degrees Fahrenheit of four cities.
Which city’s data set is bimodal?
A. City A
B. City B
C. City C
D. City D

Answers
Finding the mode of each data-set, the bimodal city's data is given by:
C. City C.
What is the mode of a data-set?It is the value that appears the most times in the data-set. If two values appear the same number of sets, the data-set is called bimodal.
Hence, looking at the table:
For City A, 10 appears three times, hence it is the only mode.For City B, 25 appears five times, hence it is the only mode.For City C, 42 and 66 each appear three times, hence they are the modes, and the data-set is bimodal.For City D, 78 appears three times, hence it is the only mode.Hence option C is correct.
More can be learned about the mode of a data-set at https://brainly.com/question/24732674
#SPJ1
PLEASE HELP 20 POINTS!!
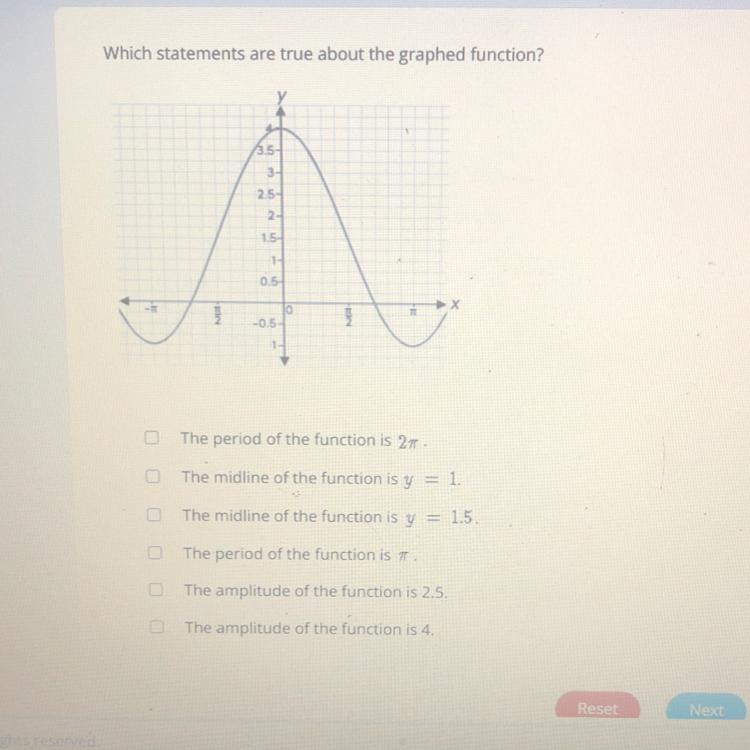
Which statements are true about the graphed function?
Answers
Step-by-step explanation:
The Amplitude is 4
The period is 2π
The midline is y=1.5
OPTION 1, 3,6
Answer:
See below ~
Step-by-step explanation:
The period of the function is 2π as it is the time taken to travel between successive troughs/crestsThe midline of the function is the mean of the highest y-value and lowest y-value ⇒ 4 - 1 / 2 = 3/2 ⇒ y = 1.5Similarly, amplitude is the distance between the top of the crest and axis ⇒ A = 4A new amusement park ride that last one minute can have up to 1,200 Riders per hour. How many riders can ride per minute.
Pls help
Answers
Answer:
20
Step-by-step explanation:
1 hour = 60 minutes
1200 riders = 60 minutes: divide by sixty to set equal to 1
20 riders = 1 minute
Just divide 1,200 by 60 because there are 60 minutes in 1 hour.
Just think about it this way: If you eat 1 banana a minute, you eat 60 bananas an hour. The amusement park ride goes around once a minute. In one hour it goes around 60 times. Each time it carries the same amount of people.
1,200 divided by 60 is...
20!
The ride can carry 20 riders each ride, and each ride lasts a minute.
PLEASE help me with this question with solutions

Answers
Answer:
D
Step-by-step explanation:
the inscribed angle intersects an arc that twice the measure of the arc interested by the central angle. The inscribed angle's arc measures 144° and the central angle's arc measures 72°
>central angle and the arc the intersected arc are equal i.e they are both 72°
>the inscribed angle is half of the measure of the intersected arc i.e since the inscribed angle is 72° the arc interested is 144°
What is the integrated rate law for a 1st order reaction?
Answers
Expiation: the half-life of a first-order reaction is independent of concentration, and this equation has the form y=mx + b so a plot of the natural log of [A] as a function of time yields a straight line
Source: khanacadamey.org
Hope this helps!
14 Jun 2018 · Norman is 12 years older than Michael. In 6 years, he will be twice as old as Michael. How old is Michael now? (A) 3 (B) 6 (C) 12
Answers
Michael is now (B) 6 years old.
Let's start by defining variables for the current ages of Norman and Michael.
Let N be Norman's current age, and M be Michael's current age.
From the problem statement, we know that N = M + 12 (Norman is 12 years older than Michael).
We also know that in 6 years, Norman will be twice as old as Michael.
So we can set up the following equation:
N + 6 = 2(M + 6)
Substituting N = M + 12 into the equation, we get:
M + 12 + 6 = 2(M + 6)
Simplifying:
M + 18 = 2M + 12
M = 6
Therefore, Michael is currently 6 years old.
Answer: (B) 6
To learn more about years here:
https://brainly.com/question/3859460
#SPJ4
Yemi is 5 years older than kunle.The product of their ages is 750. How old is kunle.
Answers
Answer:
Kunie is 25
Step-by-step explanation:
Let's make Yemi's age y, and Kunie's age k.
Because Yemi is 5 years older that Kunie, k + 5 = y.
Because the product of their ages is 750, k * y = 750.
With substitution, we can determine that k * (k + 5) = 750.
Then with distributive property we can simplify the equation to get k^2 + 5k = 750.
Then we bring all the terms to one side of the equation to get k^2 + 5k - 750 = 0.
Then with quadratics, we can factor the equation to get (k + 30)(k - 25)=0.
Thus, either k + 30 must equal 0, or k - 25 must equal 0. Thus, k must equal 25 or -30, and because someone cannot be -30 years old, k = 25.
Then, because Yemi is 5 years older than Kunie, y = 30.
Hope it helps <3
Kunle's age is marked as k.
Yemi's age is therefore k + 5.
The product of k and k + 5 equals 750.
What is k?
Now that we have tought this through...
Here is the equality:
\(k(k+5)=750\)
Expanding the parentheses and subtracting 750 from both sides gives you
\(k^2+5k-750=0\)
Which is a second degree polynomial (ie. quadratic equation).
That means there are two solutions of what Kunle's age might be.
\(k^2+5k-750=0\)
\(k^2+30k-25k-750=0\)
\(k(k+30)-25(k+30)=0\)
\((k+30) (k-25) =0\implies k_1=-30, k_2=25
\)
So we got two results and since age cannot be negative that leaves us with one result and that is 25.
TL;DR The answer is: Kunle is 25 years old.
Hope this helps.
A van loses 10% of its value every year. If its value when new was £6000, what is its value after 2 years?
Answers
Answer:
£4860
Step-by-step explanation:
To calculate the value of the van after 2 years, we need to subtract 10% of its value each year for 2 years.In the first year, the van loses 10% of its value, which is 10% of £6000.\(\sf 10\%\: of \:6000\: =\:6000 * 0.10 = 600\)
So, after the first year, the value of the van becomes£6000 - £600 = £5400
In the second year, the van loses another 10% of its value, which is 10% of £5400.\(\sf10\% \:of\: 5400 \:= 5400 * 0.10 = 540\)
So, after the second year, the value of the van becomes£5400 - £540 = £4860
Therefore, the value of the van after 2 years would be £4860.
Solve the set of two reals for the following exponential equation: \(\Large\text{${\dfrac{27^x\:-\:3^x}{9^x\:-\:3^x} = 82}$}\)
Answers
Answer: The value of the variable x in this exponential equation is 4.
The problem simply asks to solve the following exponential equation on the set of reals:
\(\begin{gathered} \bold{\dfrac{27^x~-~3^x}{9^x~-~3^x}~=~82}\\\\\\ \bold{\dfrac{\left(3^3\right )^x~-~3^x}{\left(3^2\right)^x~-~3^x}~=~82}\\\\\\ \bold{\dfrac{3^{3x}~-~ 3^x}{3^{2x}~-~3^x}~=~82}\end{gathered}\)
To solve this exponential equation in a much simpler way, what we're going to try to do is factor. Note that if we take \(\bold{ 3^x3}\)
x as a common factor what we will get is:
\( \bold{\dfrac{\not\!\!3^x\cdot\left(3^{2x}~-~1\right)}{\not\!\!3^x\cdot\left( 3^{x}~-~1\right)}~=~82}\\\\\\ \bold{ \dfrac{3^{2x}~-~1}{3^x~-~1}~=~82}\)
We can see that factoring the first part of our exponential equation resulted in a much easier exponential equation to solve. Note that \(\sf 3^{2x}~-~13\)
− 1 by the laws of exponents can be written as \(\sf \left(3^x\right)^2~-~1^ 2\)
by definition \(\sf x^2~-~y^2~=~\left(x~+~y\right)\cdot\left(x~-~y\right)\) so we have:
\(\begin{gathered} \bold{\dfrac{\left(3^x\right)^2~-~1}{3^x~-~1}~=~82} \\\\\\ \bold{ \dfrac{\left(3 ^x~+~1\right)\cdot\left(3^x~-~1\right)}{3^x~-~1}~=~82\\\\\\ 3^x~+~ 1~=~82}\\\\\\ \bold{3^x~=~81 }\end{gathered}\)
The exponential equation we now have is not at all difficult to solve. If you repeat the powers of the number 3, you can see that \(\sf 3^4\)
Is the same as 81, so we have:
\(\begin{gathered} \bold{\not\!\!3^x~=~\not\!\!3^4} \\\\\\ \boxed{\sf \bold{\therefore~x~=~4}}~~ \bold{\Rightarrow ~Answer}\end{gathered}\)
![Solve the set of two reals for the following exponential equation: [tex]\Large\text{${\dfrac{27^x\:-\:3^x}{9^x\:-\:3^x}](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/0G7N5tYPhbaVCL5mKsGHPPEmXVJZMZla.jpeg)
\(\sf{\dfrac{27^x\:-\:3^x}{9^x\:-\:3^x} = 82}\)
\(\sf{\dfrac{9^x(3^x)\:-\:3^x}{3^x(3^x)\:-\:3^x} = 82}\)
\(\sf{\dfrac{3^x(9^x-1)}{3^x(3^x-1)} = 82}\)
\(\sf{\dfrac{\cancel{3^x}(9^x-1)}{\cancel{3^x}(3^x-1)} = 82}\)
\(\sf{\dfrac{(9^x-1)}{(3^x-1)} = 82}\)
\(\sf{\dfrac{(3^x-1)(3^x+1)}{(3^x-1)} = 82}\)
\(\sf{(3^x+1)= 82}\)
\(\sf{(3^x)= 81}\)
\(\sf{(3^x)= 3^{4}}\)
\(\boxed{\bold{x= 4}}\)
I forgot how to do this. I will give brainliest!

Answers
Answer:
A = 2, B = 3 and C = 4
Step-by-step explanation:
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
Given
2x + 3y = 2 ( subtract 2x from both sides )
3y = - 2x + 2 ( divide all terms by 3 )
y = - \(\frac{2}{3}\) x + \(\frac{2}{3}\) ← in slope- intercept form
with slope m = - \(\frac{2}{3}\)
Parallel lines have equal slopes, thus
y = - \(\frac{2}{3}\) x + c ← is the partial equation
To find c substitute (2, 0) into the partial equation
0 = - \(\frac{4}{3}\) + c ⇒ c = \(\frac{4}{3}\)
y = - \(\frac{2}{3}\) x + \(\frac{4}{3}\) ← in slope- intercept form
Multiply through by 3
3y = - 2x + 4 ( add 2x to both sides )
2x + 3y = 4 ← in standard form
with A = 2, B = 3 and C = 4
a nurse is caring for a client who has depression and is taking imipramine 300 mg po divided equally every 6 hr. available is imipramine 50 mg tablets. how many tablets should the nurse administer per dose? (round the answer to the nearest tenth. use a leading zero if it applies. do not use a trailing zero.)
Answers
The nurse should administer 6 tablets per dose.
To calculate this, divide the total daily dose (300 mg) by the dose per tablet (50 mg):
300 mg / 50 mg = 6 tablets
Since the dose is divided equally every 6 hours, the nurse should administer 6 tablets every 6 hours.
It's important for the nurse to double check the medication order and dosing calculations before administering any medication to ensure the safety and well-being of the client. In addition, the nurse should monitor the client's response to the medication and report any adverse effects to the healthcare provider.
To know more about healthcare provider click on below link:
https://brainly.com/question/28463188#
#SPJ11
the biblical account of joshua's long day is a miracle of: timing intervention of natural laws visible appearance all of these
Answers
Answer:
According to search result [1], the Biblical account of Joshua's long day is a miracle of "all of these": timing, intervention of natural laws, and visible appearance.
Step-by-step explanation:
HELP ASAP PLS
a survey asked two age groups about the car color that they most preferred. the results are down in the table below. which car color eat most preferred by people ages 16-24 and what is the relative frequency within this age group?
A.) Blue, 71.4%
B.)Red, 60.6%
C.)Blue, 26.8%
D.)33.9%

Answers
Answer:
blue i think good luck
hi please help me with this i’ll give brainliest if you give a correct and show your work!

Answers
Answer:
So, A
22 divided by 5
Reduce the expression, if possible, by cancelling the common factors.
Exact Form:
22 /5
Decimal Form:
4.4
Mixed Number Form:
4 and 2 /5
Next, B
Reduce the expression, if possible, by cancelling the common factors.
Exact Form:
7 /8
Decimal Form:
0.875
Step-by-step explanation:
I hope this helps! Have a great day!
Answer:
I have boxed and highlighted the answer. Sorry for the ink to make the answers a bit messy, but the answers are :-
a. 22 ÷ 5 = 4.4
b. 7 ÷ 8 = 0.875
Hope this helps, thank you :) !!

The probability of event A is 0.53 and the probability of event B is 0.17. The probability of A and B occurring is 0.901. Which statement accurately describes these two events?

Answers
Explanation:
We're given that
P(A) = 0.53P(B) = 0.17P(A and B) = 0.901Note that P(A)*P(B) = 0.53*0.17 = 0.0901 which is somewhat similar to 0.901 but not entirely the same. We have an extra zero between the decimal point and the nine. So this indicates that \(P(A)*P(B) \ne P(\text{A and B})\). Therefore, events A and B are not independent. We consider them dependent.
Find the distance between the points!? Help

Answers
Answer:
3\sqrt(5)
or 6.71
Step-by-step explanation:
2. The car dealership sold 1,800 cars last year.
According to the chart, how
many
Mazdas
did the dealership sell?
Cars Sold by Car Dealership
Toyota
36%
Mazda
17%
Jeep
18%
Ford
29%
(A) 648
(B) 306
(C) 324
(D) 522
(E) 486

Answers
9514 1404 393
Answer:
(B) 306
Step-by-step explanation:
The chart says 17% of the 1800 cars sold were Mazdas. That number is ...
17% × 1800 = 0.17 × 1800 = 306
The dealership sold 306 Mazdas.