a company believes that travel agent a is more reliable than travel agent b. that belief is expressed on a scale from 1 to 5. identify the type of data.
Answers
The type of data expressed in the example is ordinal data.
This is an example of ordinal data, as it is data that is expressed on a scale from 1 to 5. Ordinal data is useful for comparing objects or ideas in relation to each other, and is often used to indicate levels of preference or satisfaction. In this case, the data is used to compare the reliability of two travel agents.
Ordinal data is a type of data where the values are ranked in order of magnitude. In the example given, the company has expressed their belief on a scale from 1 to 5, with higher numbers representing a higher level of reliability. Therefore, this type of data is considered ordinal.
The type of data expressed in the example is ordinal data.
Ordinal data is a type of data where the values are ranked in order of magnitude.
Learn more about data here
https://brainly.com/question/14893265
#SPJ4
Related Questions
A particle moves according to a law of motion s = f(t) = t³ - 15t + 63t, t ≥ 0 where t is measured in seconds and sin feet (a) Find the velocity at time t
(b) What is the velocity after 1 s?
(c) When is the particle at rest?
(d) WHen is the particle moving in the positive direction?
Answers
a) The velocity of the particle at any given time is v = 3t² - 15 ft/s.
b) The velocity of the particle after 1 second is v = 3(1)² - 15 = -12 ft/s.
c) The particle is at rest at t = √5 seconds.
d) The particle moves in the positive direction when t > √5 seconds.
Given the equation of motion s = t³ - 15t + 63t, we need to find the velocity of the particle at any given time, its velocity after 1 second, the instances when the particle is at rest, and when it moves in the positive direction.
The equation of motion gives us the position of the particle at any given time. To find the velocity of the particle, we need to differentiate the equation of motion with respect to time.
(a) The velocity of the particle is given by v = ds/dt. Differentiating s = t³ - 15t + 63t with respect to time, we get v = 3t² - 15. Therefore, the velocity of the particle at any given time is v = 3t² - 15 ft/s.
(b) To find the velocity of the particle after 1 second, we substitute t = 1 in the velocity equation. Therefore, the velocity of the particle after 1 second is v = 3(1)² - 15 = -12 ft/s.
(c) The particle is at rest when its velocity is zero. Therefore, we need to solve the equation 3t² - 15 = 0 to find the instances when the particle is at rest. Simplifying the equation, we get t = ±√5. Since time cannot be negative, the particle is at rest at t = √5 seconds.
(d) The particle moves in the positive direction when its velocity is positive. Therefore, we need to solve the inequality 3t² - 15 > 0 to find when the particle moves in the positive direction. Simplifying the inequality, we get t < -√5 or t > √5. Since time cannot be negative, the particle moves in the positive direction when t > √5 seconds.
For more questions like Velocity click the link below:
https://brainly.com/question/30885221
#SPJ11
Please help with this problem

Answers
Answer:
x = 2
Step-by-step explanation:
Multiply both sides by (x-5) and expand:
(x+4)/(x-5)*(x-5) = -2(x-5)
x+4 = -2x+10
Subtract 4 from both sides:
x+4-4 = -2x+10-4
x = -2x+6
Add 2x to both sides:
x+2x = -2x+6+2x
3x = 6
Divide both sides by 3:
3x/3 = 6/3
x = 2
X=2
Your welcome.
(btw the comment i made was wrong)
A table is 4.1 m and 4.1m wide. Explain how you could us Pythagorean theorem to prove that the diagonal length across the table is the same length
Answers
The opposite diagonal is 5.95m long, exact as previous diagonal in length which indicates that the table's diagonal length is the same throughout.
Define pythagorean TheoremAccording to the Pythagorean Theorem, the square of the length of the hypotenuse in every right triangle equals the sum of the squares of the lengths of the two legs.
Let's denote the width as w = 4.1m and the length as l = 4.1m. Then, the diagonal length d can be found as:
d² = w² + l²
Substituting the given values, we get:
d² = (4.1m)² + (4.1m)²
d² = 16.81m² + 16.81m²
d² = 2(16.81m²)
d = sqrt(2(16.81m²))
d ≈ 5.95m
So, we have found that the diagonal length across the table is approximately 5.95m.
Now, to prove that the diagonal length is the same length, we can repeat this calculation, but using the other diagonal of the table.
Let's denote the width as w = 4.1m and the length as l = 4.1m. Then, the other diagonal length d' can be found as:
d'² = w² + l²
Substituting the given values, we get:
d'² = (4.1m)² + (4.1m)²
d'² = 16.81m² + 16.81m²
d'² = 2(16.81m²)
d' = sqrt(2(16.81m²))
d' ≈ 5.95m
As a result, we have established that the other diagonal is roughly 5.95m long, the same as the first diagonal. This demonstrates that the table's diagonal length is the same throughout.
To know more about triangle, visit:
brainly.com/question/2773823
#SPJ1
zy is perpindicular to xy, zy=6, and xy = 8 find xz
Answers
Using the Pythagorean Theorem, it is found that xz = 10.
What is the Pythagorean Theorem?The Pythagorean Theorem relates the length of the legs \(l_1\) and \(l_2\) of a right triangle with the length of the hypotenuse h, according to the following equation:
\(h^2 = l_1^2 + l_2^2\)
In a right triangle, the sides are perpendicular, hence in this problem the sides are zy = 6 and xy = 8, while xz is the hypotenuse.
Hence, applying the Pythagorean Theorem:
(xz)² = (zy)² + (xy)²
(xz)² = 36 + 64
(xz)² = 100
xz = sqrt(100)
xz = 10.
More can be learned about the Pythagorean Theorem at https://brainly.com/question/654982
#SPJ1
Write all prime numbers between 15 and 20
Answers
Answer:
17 and 19
Step-by-step explanation:
Answer:
17, 19
Step-by-step explanation:
15 is composite (5, 3) (15, 1)
16 is composite (8, 2) (4, 4) (16, 1)
17 is prime (17, 1)
18 is composite (9, 2) (6, 3) (18, 1)
19 is prime (19, 1)
20 is composite (2, 10) (4, 5) (20, 1)
Simon and his niece marcie are comparing their ages to see if there is a mathematical connection. They find that Simon is three years more than four times marcie' age. The sum of their ages is 58. Let m be marcie's age. Could marcie be seven years old? Write an expression for Simon's age in terms of the variable m. Write and equation that models the information given Now solve for m? What is marcie's age? What is Simon's age?
Answers
Answer:
The expression for Simon's age in terms of the variable m would indicate that Simon's age is equal to four times Marcie's age plus 3:
s=4m+3 (1)
Also, you know that the sum of their ages is 58, which is:
s+m=58 (2)
You can replace (1) in (2) and solve for m to find Marcie's age:
4m+3+m=58
5m=58-3
5m=55
m=55/5
m=11
Finally, you can replace m in (1) to find Simon's age:
s=4(11)+3
s=44+3
s=47
According to this, Marcie is 11 years old and Simon is 47 years old.
Let U ={a, b, c, d, e, f, g, h, i, j, k}. Let A={d, f, g, h, i, k}. Let B={a, d, f, g, h}. Let C={a, c, f. i, k} Determine (AUC) U ( AB). Choose the correct answer below and, if necessary, fill in the answer box in your choice. OA. (AUC) U(ANB)= } (Use a comma to separate answers as needed.) OB. (A'UC) U (ANB) is the empty set. LE This Question: 1 pt Let U={x|XEN and x<9). Let A={x | E N and x is even and x 9). Let B = {x | XEN and x is odd and x <9). Let C={x | x E N and x<5). Determine the set ( A B)' UC. Select the correct answer below and, if necessary, fill in the answer box to complete your choice. A. (A B) UC = { } (Use a comma to separate answers as needed. Use ascending order) B. (ANB)'U C is the empty set. This Question: 1 pt When will n(An B)=0? Explain and give an example. (AN B)=0 when B is a subset of A. Give an example of A and B such that n(ANB)=0. O A. A={1,2,3), B = {1,3,4} OB. A={1,3), B = {2.4} O c. A={1.2.3), B = {1,3} OD. A = {1,2,3), B = {1,2,3} O E. A={1,3). 8 = {1.3.4}
Answers
n((A-B)U C) = 0
C. A={1,2,3), B = {1,3} Since B is a subset of A, (A-B) U C = C, which is the set of all natural numbers less than 5. Therefore, n((A-B)U C) = 0.
Learn more about sets
brainly.com/question/4801204
#SPJ11
Angles θ and φ are angles in standard position such that:
sinθ = -5/13 and θ terminates in Quadrant III
tanφ = -8/15 and φ terminates in Quadrant II
Find sin(θ + φ).
Answers
When \(\theta\) terminates in quadrant III, both \(\cos\theta\) and \(\sin\theta\) are negative, and
\(\sin^2\theta+\cos^2\theta=1\implies\cos\theta=-\sqrt{1-\sin^2\theta}=-\dfrac{12}{13}\)
When \(\varphi\) terminates in quadrant II, \(\cos\varphi\) is negative and \(\sin\varphi\) is positive, so
\(1+\tan^2\varphi=\sec^2\varphi\implies\sec\varphi=-\dfrac{17}{15}\)
which gives
\(\cos\varphi=\dfrac1{-\frac{17}{15}}=-\dfrac{15}{17}\)
\(\tan\varphi=\dfrac{\sin\varphi}{\cos\varphi}=-\dfrac8{15}\implies\sin\varphi=\dfrac8{17}\)
Now,
\(\sin(\theta+\varphi)=\sin\theta\cos\varphi+\cos\theta\sin\varphi=-\dfrac{21}{221}\)
(q007) identify the true statement. group of answer choices p-waves and s-waves are seismic surface waves. s-waves are compressional body waves, while p-waves are shear body waves. surface waves are the first to show up on a seismogram recording of a quake. surface waves typically have the largest amplitude.
Answers
In this case, the true statement is that surface waves typically have the largest amplitude.
Explanation:
What are seismic waves?
Seismic waves are vibrations that travel through the earth's layers and carry the energy from an earthquake's release. Seismic waves are divided into two main types: body waves and surface waves.
Body waves are waves that travel through the earth's interior and have two different types: P-waves, or primary waves, and S-waves, or secondary waves.
Surface waves are the waves that travel along the earth's surface and are responsible for the most significant destruction during an earthquake. Surface waves are divided into two types: Rayleigh waves and Love waves.
Surface waves typically have the largest amplitude, which means that they are the ones that shake the most and cause the most significant destruction.
Learn more about Body Waves here:
https://brainly.com/question/3901556
#SPJ11
Write an explicit formula for a_n , the n^{th} term of the sequence 125, 25, 5, ...
Answers
The explicit formula for the sequence is \(a_n = 125 \times (\frac{1}{5})^{n-1}\).
Describe Geometric Sequence.A geometric sequence is a sequence of numbers in which each term is obtained by multiplying the previous term by a fixed constant. This fixed constant is called the common ratio and is denoted by the letter r.
\(\mathrm{ \large{a_n }= a_1 \times r^{n-1} }\)
where aₙ is the nth term of the sequence, a₁ is the first term of the sequence, r is the common ratio, and n is the position of the term in the sequence.
The common ratio of a geometric sequence determines how quickly the terms increase or decrease. If the common ratio is greater than 1, the terms will increase exponentially. If the common ratio is between 0 and 1, the terms will decrease exponentially. If the common ratio is negative, the terms will alternate between positive and negative values.
The sum of a finite geometric sequence can be calculated using the formula:
\($\mathrm{S_n = a_1 \times \frac{1-r^n}{1-r}}\)
Geometric sequences have applications in many areas of mathematics and science, including finance, physics, and computer science. They are used to model exponential growth and decay, as well as to analyze patterns in data and algorithms.
The given sequence is a geometric sequence with a common ratio of 1/5. The first term is 125.
The explicit formula for a geometric sequence is given by:
\(\mathrm{ \large{a_n }= a_1 \times r^{n-1} }\)
where a₁ is the first term and r is the common ratio.
Substituting the given values, we get:
\(a_n = 125 \times (\frac{1}{5})^{n-1}\)
Hence, the explicit formula for the sequence is \(a_n = 125 \times (\frac{1}{5})^{n-1}\).
To know more about sequence visit:
brainly.com/question/28615767
#SPJ1
During the next 4 months the SureStep Company is forecasted the following demands for pairs of shoes: Month 1 Month 2 Month 4 Demand 3000 5000 Month 3 2000 1000 At the beginning of month 1,500 pairs of shoes are on hand (already produced previously and not sold). and SureStep has 100 workers. A worker is paid E 1500 per month. Each worker can work up to 160 hours a month before he or she receives overtime. A worker may be forced to work up to 20 hours of overtime per month and is paid E 13 per hour for overtime labor. It takes 4 hours of labor and E 15 of raw material to produce a pair of shoes. At the beginning of each month, workers can be hired or fired. Each hired worker costs E 1600, and each fired worker costs E 2000. At the end of each month, a holding cost of E3 per pair of shoes left in inventory is incurred. Production in a given month can be used to meet that same month's demand. Back ordering is allowed and comes at the cost of E5 per pair of shoes due to administrative costs. Draw up three possible aggregate plans (one level plan, one chase plan with overtime, one chase plan without using overtime), and give your advice to SureStep's operations manager which one to follow and why. Submit your Excel file here.
Answers
Based on the provided information, three possible aggregate plans for SureStep Company are:
Level Plan: Produce a constant number of shoes each month to match the average demand over the four months.
Chase Plan with Overtime: Adjust the workforce level each month to match the demand exactly, utilizing overtime when necessary.
Chase Plan without Overtime: Adjust the workforce level each month to match the demand exactly, without using overtime.
To determine the best aggregate plan, we need to evaluate each plan based on the given criteria. Let's analyze each plan in detail:
Level Plan:
In this plan, SureStep Company produces a constant number of shoes each month to match the average demand over the four months. This means the product will be 4,750 pairs of shoes per month ([(3000+5000+2000+1000)/4]). By using a level plan, SureStep aims to have a stable production rate and maintain a steady workforce.
Chase Plan with Overtime:
In this plan, SureStep adjusts the workforce level each month to match the demand exactly. The company utilizes overtime when necessary to meet the demand. By hiring or firing workers, they can achieve the required workforce level. The number of workers required each month is calculated by dividing the demand for that month by the regular working hours per worker (160 hours) and rounding it up to the nearest whole number. If the demand exceeds the capacity even with regular working hours, overtime is used.
Chase Plan without Overtime:
Similar to the Chase Plan with Overtime, SureStep adjusts the workforce level each month to match the demand exactly. However, in this plan, overtime is not utilized. The number of workers required each month is calculated the same way as in the previous plan, but if the demand exceeds the capacity even with regular working hours, the excess demand is back-ordered.
To decide which plan to follow, we need to consider various factors such as costs, customer satisfaction, and overall company objectives. Here are some points to consider:
Level Plan: This plan provides a consistent production rate and helps in managing inventory levels efficiently. However, it may result in higher holding costs due to excess inventory. Also, it may lead to customer dissatisfaction if there are significant variations in demand during the four months.
Chase Plan with Overtime: This plan allows SureStep to meet the exact demand each month by adjusting the workforce level and utilizing overtime when necessary. It helps in minimizing holding costs and back-ordering costs. However, overtime labor costs and the cost of hiring/firing workers should be considered. It may also lead to potential employee fatigue due to overtime work.
Chase Plan without Overtime: This plan aims to meet the exact demand each month without utilizing overtime. It helps in minimizing overtime labor costs but may result in higher back-ordering costs and potential customer dissatisfaction due to delayed deliveries.
Based on the specific cost and customer satisfaction preferences of SureStep Company, the operations manager needs to evaluate the trade-offs and select the most suitable aggregate plan. The decision may involve analyzing the financial impact, evaluating customer service levels, and considering the company's overall strategy and goals.
For more questions like Company click the link below:
https://brainly.com/question/30532251
#SPJ11
In 1994 , the moose population in a park was measured to be 4280 . By 1998 , the population was measured again to be 4800 . If the population continues to change linearly: A.) Find a formula for the moose population, P, in terms of t, the years since 1990. P(t)= B.) What does your model predict the moose population to be in 2006 ?
Answers
To find a formula for the moose population, P, in terms of t, the years since 1990, we need to determine the rate of change in population over time. Given two data points, we can use the slope-intercept form of a linear equation.
Let t = 0 correspond to the year 1990. We have two points: (4, 280, 1994) and (8, 4800, 1998). Using the formula for the slope of a line, m = (y2 - y1) / (x2 - x1), we can calculate the slope:
m = (4800 - 4280) / (8 - 4)
Simplifying, we get m = 130 moose per year. Now, we can use the point-slope form of a linear equation to find the formula:
P - 4280 = 130(t - 4)
Simplifying further, we get P(t) = 130t + 4120.
To predict the moose population in 2006 (t = 16), we substitute t = 16 into the formula:
P(16) = 130(16) + 4120 = 2080 + 4120 = 6200.
Therefore, the model predicts the moose population to be 6200 in 2006.
To know more about linear equations click here: brainly.com/question/32634451
#SPJ11
If profits decrease by 13.8% when the degree of operating
leverage (DOL) is 3.8, then the decrease in sales is:
A) 0.28%
B) 0.52%
C) 3.63%
D) 10%
E) 52.44%
Answers
Given that profits decrease by 13.8% when the degree of operating leverage (DOL) is 3.8.
The decrease in sales is: We have to determine the percentage decrease in sales Let the percentage decrease in sales be x.
Degree of Operating Leverage (DOL) = % change in Profit / % change in Sales3.8
= -13.8% / x Thus, we have: x
= -13.8% / 3.8
= -3.63%Therefore, the decrease in sales is 3.63%.Hence, the correct option is C) 3.63%. Percentage decrease in sales = % change in profit / degree of operating leverage
= 13.8 / 3.8
= 3.63% The percentage decrease in sales is 3.63%.
To know more about profits, visit:
https://brainly.com/question/29987711
#SPJ11
will give brainlist or whatever.
Meredith has $5.10 in quarters and dimes. She has 24 coins in all. How many quarters and how many dimes does she have?
Answers
Write the expression in words.
2x + 2=
Answers
Answer:
um
two times x plus two equals _
Step-by-step explanation:
two plus the sum of two times a number
MY LAST QUESTION PLEASE HELP
Given the special right triangle below, what is the value of the hypotenuse?
30°
60°
6
A
6
B
673
С
123
D
12

Answers
Answer:
12
Step-by-step explanation:
Since this is a right triangle, we can use trig functions
cos theta = adj / hyp
cos 60 = 6/hyp
hyp = 6 / cos 60
hyp = 6 / (1/2)
htp = 12
A line contains the points (-4, 2) and (-4, 6). The line is translated 3 units to the right and 2 units down. What are the new points on the translated line? The new point for (-4, 2) is: () The new point for (-4, 6) is: ()
Answers
The new points after the translation are (1, 0) and (1, 4)
What are the new points on the translated line?A translation of 3 units to the right and 2 units down, applied to a general point (x, y), gives:
(x + 3, y - 2)
Here we know that one line passes through the points (-4, 2) and (-4, 6). (so this is a vertical line)
If we apply the translation, we will get:
(-4 + 3, 2 - 2) = (1, 0)
(-4 + 3, 6 - 2) = (1, 4)
These are the new points of the line.
Learn more about translations at:
https://brainly.com/question/24850937
#SPJ1
a+hedge+fund+returns+on+average+26%+per+year+with+a+standard+deviation+of+12%.+using+the+empirical+rule,+approximate+the+probability+the+fund+returns+over+50%+next+year.
Answers
Based on the empirical rule, the probability that the hedge fund returns over 50% next year is approximately 5%.
The empirical rule, also known as the 68-95-99.7 rule, is a statistical guideline that applies to a normal distribution (also called a bell curve). It states that for a normal distribution:
Approximately 68% of the data falls within one standard deviation of the average.
Approximately 95% of the data falls within two standard deviations of the average.
Approximately 99.7% of the data falls within three standard deviations of the average.
In this case, we know the average return of the hedge fund is 26% per year, and the standard deviation is 12%. We want to approximate the probability that the fund returns over 50% next year.
To do this, we need to determine how many standard deviations away from the average 50% falls. This can be calculated using the formula:
Z = (X - μ) / σ
Where:
Z is the number of standard deviations away from the average.
X is the value we want to find the probability for (50% in this case).
μ is the average return of the hedge fund (26% per year in this case).
σ is the standard deviation (12% in this case).
Let's calculate the Z-value for 50% return:
Z = (50 - 26) / 12
Z ≈ 24 / 12
Z = 2
Now that we have the Z-value, we can refer to the empirical rule to estimate the probability. According to the rule, approximately 95% of the data falls within two standard deviations of the average. This means that there is a 95% chance that the hedge fund's return will fall within the range of (μ - 2σ) to (μ + 2σ).
In our case, the range is (26 - 2 * 12) to (26 + 2 * 12), which simplifies to 2 to 50.
To know more about average here
https://brainly.com/question/16956746
#SPJ4
HELP! The function f is defined above. For what value of k, if any, is f continuous at x=-7
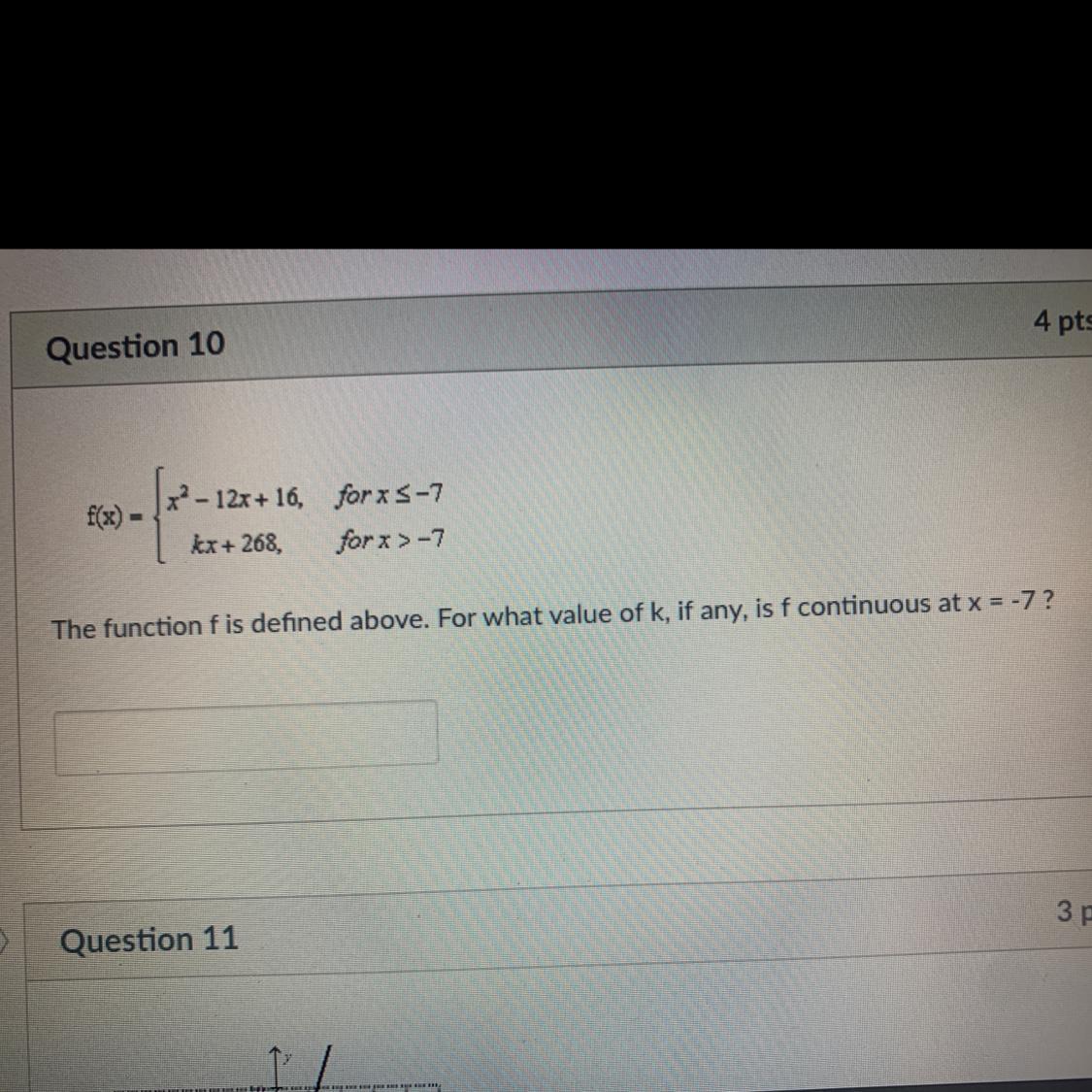
Answers
In order for the function to be continuous at x = -7, the limits from either side as x approaches -7 must be equal:
\(\displaystyle \lim_{x\to-7^-} f(x) = \lim_{x\to-7}(x^2-12x+16) = 149\)
\(\displaystyle \lim_{x\to-7^+} f(x) = \lim_{x\to-7}(kx+268) = -7k+268\)
Solve for k :
149 = -7k + 268
7k = 119
k = 17
The function f(x) is continuous at x = -7 if and only if k = 41. This is because for continuity to hold at x = -7, the value of k must be such that the left-hand limit, right-hand limit, and the actual value of the function at x = -7 are equal. In this case, the value of k that satisfies this condition is k = 41.
For a function to be continuous at a specific point, the following conditions must be satisfied:1. The function must be defined at that point (i.e., the function should have a value at x = -7).
2. The limit of the function as x approaches -7 from the left must be equal to the limit of the function as x approaches -7 from the right.
3. The value of the function at x = -7 must be equal to the limits mentioned in condition 2.
Let's go through each of these conditions step by step for the given function:
Given function:
f(x) = { \(x^2 - 12x + 16\), for x <= -7
kx + 268, for x > -7
1. The function must be defined at x = -7:The function is defined at x = -7 for the first part of the piecewise definition: x^2 - 12x + 16. So, this condition is satisfied.
2. The limit from the left must be equal to the limit from the right as x approaches -7:We need to calculate the limits as x approaches -7 from the left (LHL) and from the right (RHL) for the second part of the piecewise definition: kx + 268.
LHL as x approaches -7: lim (x->-7-) [kx + 268] = -7k + 268.
RHL as x approaches -7: lim (x->-7+) [kx + 268] = -7k + 268.
Since both the left-hand limit and the right-hand limit are equal (-7k + 268), this condition is satisfied.
3. The value of the function at x = -7 must be equal to the limits: \(f(-7) = -7^2 + 12 * 7 + 16 = 49 - 84 + 16 = -19.\)
The limits from conditions 2 are -7k + 268.
To have continuity, the value of the function at x = -7 must be equal to the limits: -19 = -7k + 268.
Solving for k: -7k = -19 - 268
-7k = -287
k = 41.
So, for the function f to be continuous at x = -7, the value of k must be 41.
To know more about continuous:
https://brainly.com/question/31523914
#SPJ3
+
ht
3
4
-1
2
+
2
4
15-1 -
0 1
A==
+
1
3
? Use the number line to explain your
3
4
answer.
No, because
is to the left of
4
3
4
O No, because
is to the right of
4
4
Yes, because
is to the left of
4
3
4
Yes, because
is to the right of
4.
3
4

Answers
Answer: B.) No, because - 1/4 is to the right of - 3/4
That was the answer I got it right!!!
PLEASE HELP!! NO LINKS!!

Answers
Answer: 95
Step-by-step explanation:
360 - 265 = 95
If f(x)=-3x+4 and g(x)=2, solve for the value of x for which f(x)=g(x) is true
Answers
Answer: 2/3
Step-by-step explanation:
Fx) = g(x)
−3x + 4 = 2
-3x + 4 - 4 = 2 - 4
-3x = -2
Dividing by -3 on both sides;
(-3x)/-3 = (-2)/-3
x = 2/3
Given that slope = -1 and a point (3,-1), write an equation in slope-
intercept form of the line,
у
X +
Answers
Slope/M= -1
X= 3
Y= -1
-1 = -1(3)+b
-1 = -3 + b
Add +3 to -3 and -1 to cancel -3 out to get (b)
-3+3 = 0 cancel it
-1 +3 = 2
So, b = 2
In an equation it will be written as
y= -1x + 2
In standard form it will be
1x + y = 2
But your official answer will be
B= 2
Y= -1x+2
20% of what number is 24
Answers
Answer:
20% of 120 is 24.
Step-by-step explanation:
i need to write 20 letters
Please help me with math

Answers
The set of numbers from least to greatest is-
5×10⁻², 6%, 2/5, 4/9, 2⁻¹, √3.
What is referred as the ascending order?The arrangement of numbers or even other items in order of increasing from smallest to largest is referred to as ascending order. Ascending order is represented by numbers that emerge on a number line from left to right. We generally represent it with commas or by using the 'less-than symbol (<)' between numbers.For the given numbers;
The given number are-
2/5, 5×10⁻², √3, 6%, 4/9, 2⁻¹.
These number can be written in the decimal form as;
2/5 = 0.405×10⁻² = 0.058√3 = 1.7326% = 0.064/9 = 0.442⁻¹ = 0.5Now arrange the number from least to greatest.
0.058, 0.06, 0.40, 0.44, 0.5, 1.73
Convert the number in given form.
5×10⁻², 6%, 2/5, 4/9, 2⁻¹, √3.
Thus, the number represented in the ascending order are-
5×10⁻², 6%, 2/5, 4/9, 2⁻¹, √3.
To know more about the ascending order, here
https://brainly.com/question/12783355
#SPJ13
Write the converse, inverse and contrapositive of the followingIf the triangle is equilateral, then the triangle is equiangular
Answers
this is the answer gimme brainliest

plz help first one who answers gets brainlyest

Answers
Tax: $0.28
New Subtotal: $3.76
Hope this helps!
I bought a pack of 100 rectangular index cards. Each card measured 15 cm by 10 cm. The pack said: paper density=200gsm (grams per square metre). This means that a square metre of these cards weighs 200 g.
All the cards in the pack are placed flat on a table without overlap. In square metres, what is the total area of the table covered by the cards?
Answers
Answer:
15,000cm^2
Step-by-step explanation:
Given data
Dimension of a card
Length= 15cm
Widht= 10cm
Area= 15*10= 150cm^2
Now if 1 card covers area of 150cm^2
the 100 cards will cover x
cross multiply
x= 150*100
x= 15,000cm^2
Hence the total area covered is 15,000cm^2
assume that the population germination time is normally distributed. find the 97% confidence interval for the mean germination time.
Answers
The 97% confidence interval for the mean germination time is (13.065, 18.535) (option a).
To find the 97% confidence interval for the mean germination time based on the provided data, we can calculate the interval using the t-distribution since the sample size is small (n = 10) and the population standard deviation is unknown.
Using statistical software or a t-distribution table, the critical value for a 97% confidence level with 10 degrees of freedom is approximately 2.821.
Calculating the sample mean and sample standard deviation from the given data:
Sample mean (\(\bar x\)) = (18 + 12 + 20 + 17 + 14 + 15 + 13 + 11 + 21 + 17) / 10 = 15.8
Sample standard deviation (s) = √[(Σ(xᵢ - \(\bar x\))²) / (n - 1)] = √[(6.2² + (-3.8)² + 4.2² + 1.2² + (-1.8)² + (-0.8)² + (-2.8)² + (-4.8)² + 5.2² + 1.2²) / 9] = 4.652
Now we can calculate the confidence interval:
Confidence Interval = sample mean ± (critical value * (sample standard deviation / √(sample size)))
Confidence Interval = 15.8 ± (2.821 * (4.652 / √10))
Confidence Interval ≈ (13.065, 18.535)
Therefore, the correct option for the 97% confidence interval for the mean germination time is A. (13.065, 18.535).
To know more about confidence interval:
https://brainly.com/question/32546207
#SPJ4
The complete question is:
Recorded here are the germination times (in days) for ten randomly chosen seeds of a new type of bean. Assume that the population germination time is normally distributed. Find the 97% confidence interval for the mean germination time.
18, 12, 20, 17, 14, 15, 13, 11, 21 and 17
A. (13.065, 18.535)
B. (13.063, 18.537)
C. (13.550, 21.050)
D. (12.347, 19.253)
E. (14.396, 19.204)
Olivia and her three siblings bring a sack lunch to school each day, consisting of a bagel, an apple, a cookie, and a juice box. When Olivia's mom goes grocery shopping, she likes to purchase the same amount of each lunch item so that she can make complete lunches, with no leftover items. However, each item comes in a different sized package, as shown below: Bagels: six in a bag Apples: eight in a bag Cookies: twelve in a box Juice Boxes: nine in a box Find the least number of packages she must purchase in order to have the same amount of each item.
Olivia's mom should purchase how many bags of apples?
Answers
Answer:
72
Step-by-step explanation:
Find the LCM
6=2x3
8=2x2x2
9=3x3
12=2x2x3
LCM=2³x3²
=72