A community center offers yoga classes for $8 per month plus an additional $0.25 per center floor mat used.
Write an equation to express this relationship, using m to represent the number of mats used per month and C to represent the total cost in dollars.
Answers
X represents the amount of center floor mats used
Related Questions
b/5 - 3 = 3
What is the value of 3?
Answers
Answer:
wait huh?
Step-by-step explanation:
cdzfv
c
c
c
c
c
Solve 2x^2 - 3x = 12 using the quadratic formula.
A) x = 3/4+√105/4i, x = 3/4-√105/4i
B) x = 3/4+√87/4i, x = 3/4-√87/4i
C) x = 3/4 + √87/4, x = 3/4-√87/4
D) x = 3/4 + √105/4, x = 3/4-√105/4
Answers
Answer:
\(x = \frac{3}{4} + \frac{ \sqrt{105} }{4} \: \: , \: \: \: x = \frac{3}{4} - \frac{ \sqrt{105} }{4} \\ \)
Step-by-step explanation:
2x² - 3x - 12 = 0
Using the quadratic formula which is
\(x = \frac{ - b \pm\sqrt{ {b}^{2} - 4ac} }{2a} \\ \)
From the question
a = 2 , b = - 3 , c = - 12
So we have
\(x = \frac{ - - 3\pm \sqrt{ ({ - 3})^{2} - 4(2)( - 12)} }{2(2)} \\ = \frac{3\pm \sqrt{9 + 96} }{4} \\ = \frac{3\pm \sqrt{105} }{4} \: \: \: \: \: \: \)
Separate the solutions
We have the final answer as
\(x = \frac{3}{4} + \frac{ \sqrt{105} }{4} \: \: , \: \: \: x = \frac{3}{4} - \frac{ \sqrt{105} }{4} \\ \)
Hope this helps you
is the equation a true statement when x equals -3 in other words is -3 a solution to the equation 6 x + 5 = 5x +8 + 2x explained? explain
Answers
Answer: Yes
Step-by-step explanation: bc 6(-3)+5=5(-3)+8+2(-3)
Becomes -18+5=-15+8+-6 which equals -13 on both sides meaning -3 is a solution
6x+5=5x+8+2x
6x+5=(5x+2x)+(8)(Combine Like Terms)
6x+5=7x+8
6x+5=7x+8
Step 2: Subtract 7x from both sides.
6x+5−7x=7x+8−7x
−x+5=8
Step 3: Subtract 5 from both sides.
−x+5−5=8−5
−x=3
Step 4: Divide both sides by -1.
−x
−1
=
3
−1
x=−3
Answer:
x=−3
i need help with math

Answers
The relationship between the distance that birds fly in relation to the time they do so, is positive.
There are about 3 outliers but for the most part, the relationship is positive.
How to describe the relationship ?The graph which shows the distance that birds fly in relation to the time they do, shows that there is a positive relationship because as the time increases, the distance that the birds have flown also increases.
There are some outliers such as the bird that flew 1 mile in 7 hours but in general, as the time increases, the distance increases as well. There are two clusters of distance as well.
Find out more on relationship at https://brainly.com/question/1599922
#SPJ1
Kiran reads 5 pages in 20 minutes. He spends the same amount of time per page. How long will it take him to read 11 pages? Do not include units (in minute) in your answer. If you get stuck, consider using the table.
Answers
Answer:
44 minutes
Step-by-step explanation:
It takes him 4 minutes to read one page, so you multiple 4 by 11 and get the amount of time it takes him to read 11 pages
Answer:
takes 44 minutes to read 11 pages
Step-by-step explanation:
Help would be much appreciated

Answers
standard form two thousand, fifty seven and eighteen hundredths
Answers
Answer:
2,057.18
Step-by-step explanation:
Each volleyball set costs $63.74.
Which equation represents the cost, c, of n sets?
Answers
The equation that represents the cost, c, of n sets is c = 63.74n
Which equation represents the cost, c, of n sets?from the question, we have the following parameters that can be used in our computation:
Each volleyball set costs $63.74.
Let the total number of sets be n
So we have
Cost of n = 63.74 * n
This gives
c = 63.74n
Hence, the equation is c = 63.74n
Read more about equation at
https://brainly.com/question/32492977
#SPJ1
Please help thank you all so much

Answers
The domain of the composite functions:
a). (f + g)(-2) = 23
b). (f - g) (-2) = 1
c). f(x) - g(x) = x² - 5x - 13
What is composite function?A function is composite when the co- domain of the first mapping is the domain of the second mapping
Given the functions f(x) = x² - 4x and g(x) = x + 13, we shall evaluate the domains of the functions as follows:
a). (f + g)(-2) = (-2)² - 4(-2) + (-2) + 13
(f + g)(-2) = 4 + 8 - 2 + 13
(f + g)(-2) = 23
b). (f - g) (-2) = (-2)² - 4(-2) - (-2) - 13
(f - g)(-2) = 4 + 8 + 2 - 13
(f - g) (-2) = 1
c). f(x) - g(x) = x² - 4x - x - 13
f(x) - g(x) = x² - 5x - 13
Therefore, the domain of the composite functions:
a). (f + g)(-2) = 23
b). (f - g) (-2) = 1
c). f(x) - g(x) = x² - 5x - 13
Read more about composite function here:https://brainly.com/question/10687170
#SPJ1
Write an equivalent
unit rate to eating 5
potato chips in 1/4 of a
minute.
Answers
Answer:
1 potato chip every 3 seconds
Step-by-step explanation:
Answer:
20 chips in one minute
Step-by-step explanation:
multiply each number by 5
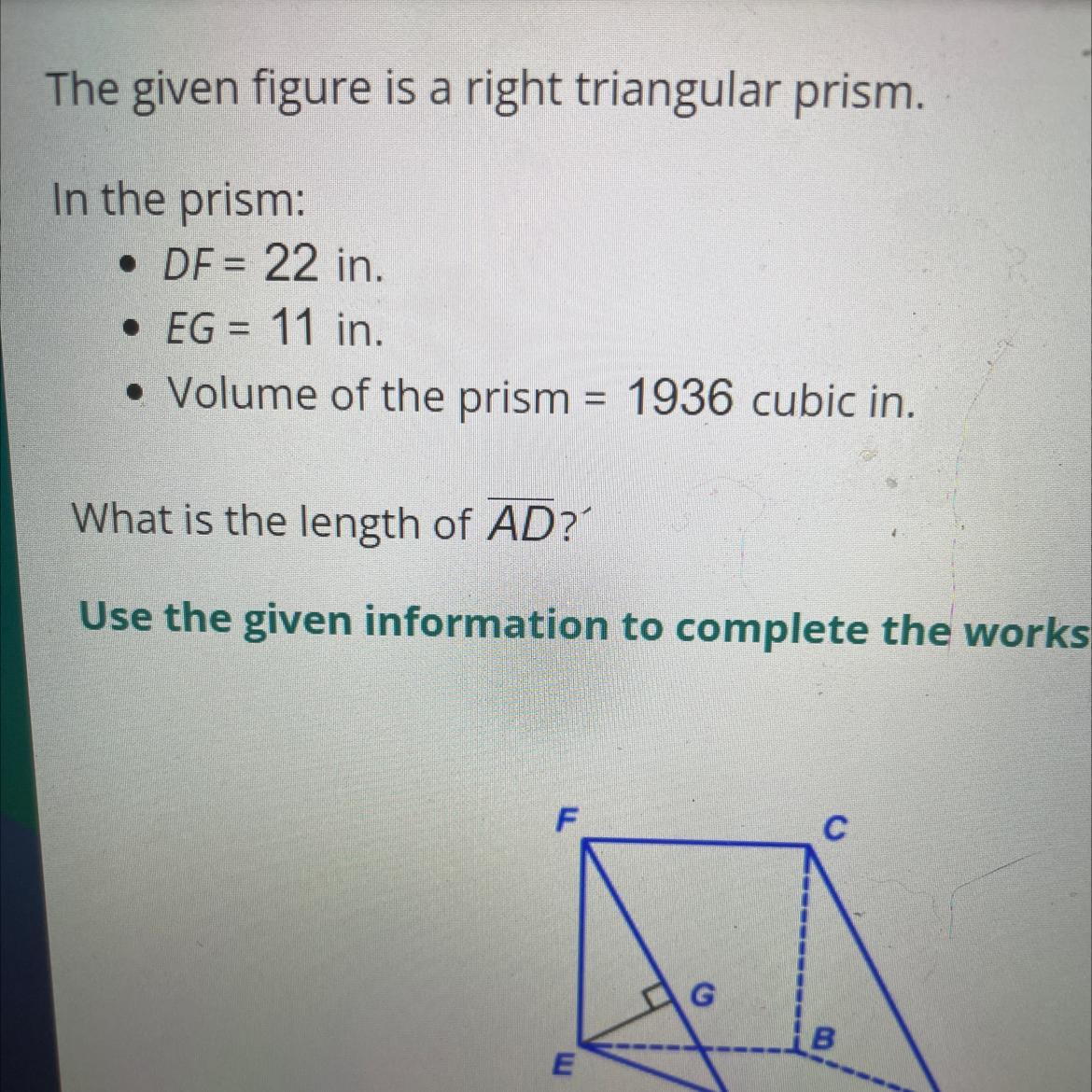
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
The high school drama club earned $855 after selling 255 tickets. The student tickets were $1 each, and guest tickets were $5 each. How many students and guest tickets were sold?
Answers
Answer:
Step-by-step explanation:
20 tickets were sold to guest and 235 were sold to guest
Got to say what a school
Number of student tickets are 105 and the number of guest tickets are 150.
What is an Equation?An equation is the statement of two expressions located on two sides connected with an equal to sign. The two sides of an equation is usually called as left hand side and right hand side.
Let x be the number of student tickets and y be the number of guest tickets sold.
The high school drama club earned $855 after selling 255 tickets.
x + y = 255
Given,
Cost of one student ticket = $1
Cost of one guest ticket = $5
x + 5y = 855
Thus we get two linear equations :
x + y = 255
x + 5y = 855
Solving this, we will get the number we need.
Subtracting the first equation from the second one,
4y = 600
y = 600 / 4
y = 150
x = 255 - y
= 255 - 150
= 105
Hence the high school drama club sold 105 student tickets and 150 guest tickets.
To learn more about Equations, click :
https://brainly.com/question/10413253
#SPJ2
A soft drink manufacturer wishes to know how many soft drinks adults drink each week. They want to construct a 95% confidence interval with an error of no more than 0.08. A consultant has informed them that a previous study found the mean to be 3.1 soft drinks per week and found the variance to be 0.49. What is the minimum sample size required to create the specified confidence interval? Round your answer up to the next integer.
Answers
Answer:
The minimum sample size required to create the specified confidence interval is 295.
Step-by-step explanation:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.95}{2} = 0.025\)
Now, we have to find z in the Z-table as such z has a p-value of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.025 = 0.975\), so Z = 1.96.
Now, find the margin of error M as such
\(M = z\frac{\sigma}{\sqrt{n}}\)
In which \(\sigma\) is the standard deviation of the population and n is the size of the sample.
Variance of 0.49:
This means that \(\sigma = \sqrt{0.49} = 0.7\)
They want to construct a 95% confidence interval with an error of no more than 0.08. What is the minimum sample size required to create the specified confidence interval?
The minimum sample size is n for which M = 0.08. So
\(M = z\frac{\sigma}{\sqrt{n}}\)
\(0.08 = 1.96\frac{0.7}{\sqrt{n}}\)
\(0.08\sqrt{n} = 1.96*0.7\)
\(\sqrt{n} = \frac{1.96*0.7}{0.08}\)
\((\sqrt{n})^2 = (\frac{1.96*0.7}{0.08})^2\)
\(n = 294.1\)
Rounding up:
The minimum sample size required to create the specified confidence interval is 295.
Solve for the value of q

Answers
Answer:
\(q=45\)
Step-by-step explanation:
Notice that \((q+2)^{\circ}\) and \((3q-2)^{\circ}\) form a linear pair, that is, they sum to \(180^{\circ}\) as follows:
\((q+2)^{\circ}+(3q-2)^{\circ}=180^{\circ}\\(q+2+3q-2)^{\circ}=180^{\circ}\\(4q)^{\circ}=180^{\circ}\\4q=180\\q=\frac{180}{4}\\q=45\)
please help me asap

Answers
Answer:
Step-by-step explanation:
it is B
A bag contains 1 purple beads and 3 green beads. A bead is drawn and then replaced before drawing the second bead. Find the probability both beads
drawn are green.
6
~
7
Answers
ggg
Step-by-step explanation:
Answer:
9/16
Step-by-step explanation:
There are 4 beads in the bag, 1 purple and 3 green
P ( green) = green/total
= 3/4
The bead is replaced
There are 4 beads in the bag, 1 purple and 3 green
P ( green) = green/total
= 3/4
P ( green, replace, green) =P( green) * P ( green)
= 3/4 * 3/4
= 9 /16
ou are working with the penguins dataset. you want to use the summarize() and mean() functions to find the mean value for the variable body mass g. you write the following code: penguins %>% drop na() %>% group by(species) %>% add the code chunk that lets you find the mean value for the variable body mass g.
Answers
The mean body mass of the Adelie species is 3706.164 g.
Original chunk of code:
penguins %>%
drop_na() %>%
group_by(species) %>%
The code chunk summarize(mean(body_mass_g)) lets you find the mean value for the variable body_mass_g. The correct code is
penguins %>% drop_na() %>% summarize (mean(body_mass_g)).
The summarize () function displays summary statistics. We can use the summarize() function in combination with other functions - such as mean(), max(), min() - to calculate specific statistics. In this case, you use mean() to calculate the mean value for body mass.
Hence, The mean body mass for the Adelie species is 3706.164 g.
To learn more about mean body mass click here :
brainly.com/question/11050881
#SPJ4
16 families went on a trip which cost them Rs 2,16,352. How much did each
family pay?
Answers
Given that 16 families went on a trip and the cost of the trip was Rs. 2,16,352.The amount paid by each family is to be determined by unitary method Hence each family paid Rs.13522
Now, let's solve this by using the method of unitary method. To find the cost of 1 family trip, we will divide the total cost of the trip by the number of families.2,16,352 / 16 = 13,522 So, the cost of the trip per family is Rs. 13,522.Hence, each family paid Rs. 13,522 for the trip.
to know more about unitary method
https://brainly.com/question/28276953
Answer:
Step-by-step explanation
1. The total cost of the trip for all 16 families is Rs 2,16,352.
2. To find out how much each family paid, we need to divide the total cost by the number of families: Rs 2,16,352 ÷ 16.
3. When we do the division, we get the result: Rs 13,522.
Now let's check if this result is correct:
1. If each family paid Rs 13,522 for the trip, then the total cost for all 16 families would be: 16 × Rs 13,522 = Rs 2,16,352.
2. This is exactly the same as the total cost given in the problem statement.
So we have shown that each family paid **Rs 13,522** for the trip
Part of the American romantic transcendental belief system included a turning away from the negative effects of industrialization and corruption in the cities.
Where did these transcendentalists turn for respite?
Answers
Answer:
NatureStep-by-step explanation:
acellus
The American romantic transcendental turn for respite nature.
What is the city?A permanent, densely populated area with a clearly defined territorial area is what is meant by a city. Most cities have advanced equipment for housing, transport, sanitation, utilities, land use, manufacturing, and telecommunications.
The Transcendentalists worshipped nature. Instead of being beneath mankind, nature served as the additional half of a symbiotic association. The transcendental perspective of environment and the individuality of a person is based on this analogy.
The idea is that in order to connect with God via nature, mankind must transcend the physical and almost all materialistic world. These all reaffirm the core tenets of transcendentalism: freedom of thought, independence and nonconformity, personal development, and regeneration.
Learn more about city, Here:
https://brainly.com/question/24476050
#SPJ2
Write an equation for the line parallel to y =-2/3x – 7 that contains (-6, 3).
Answers
keeping in mind that parallel lines have exactly the same slope, let's check for the slope of the equation above
\(y = \stackrel{\stackrel{m}{\downarrow }}{-\cfrac{2}{3}}x-7\qquad \impliedby \qquad \begin{array}{|c|ll} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}\)
so, we're really looking for the equation of a line whose slope is -2/3 and passes through (-6 , 3)
\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{3})\qquad \qquad \stackrel{slope}{m}\implies -\cfrac{2}{3} \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{3}=\stackrel{m}{-\cfrac{2}{3}}(x-\stackrel{x_1}{(-6)})\implies y-3=-\cfrac{2}{3}(x+6) \\\\\\ y-3=-\cfrac{2}{3}x-4\implies y=-\cfrac{2}{3}-1\)
The equation for the line parallel to y =-2/3x – 7 that contains (-6, 3) is y - 3 = -2/3(x+6)
Equation of a line in parallel formThe equation of a line in point slope form is expressed as:
y - y1 = m(x-x1)
m is the slope
(x1, y1) is any point on the line
GIven the equation y =-2/3x – 7, the slope of the line is -2/3
Substitute m = -2/3 and (-6, 3) into the formula
y - 3 = -2/3(x-(-6)
y - 3 = -2/3(x+6)
Hence the equation for the line parallel to y =-2/3x – 7 that contains (-6, 3) is y - 3 = -2/3(x+6)
Learn more on equation of aline here: https://brainly.com/question/13763238
What term number will have 400 square in it?
Answers
Answer:
400^2 = 160 000
Step-by-step explanation:
The square of a number means the product of a number by itself, while the perfect square ... For example, the number 9 is a perfect square because it can be expressed as a product of ... A square football pitch has a perimeter of 400 meters.
determine what type of model bets fits the given situation: A $500 raise in salary each year
Answers
The type of model that best fits the situation of a $500 raise in salary each year is a linear model.
In a linear model, the dependent variable changes a constant amount for constant increments of the independent variable.
In the given case, the dependent variable is the salary and the independent variable is the year.
You may build a table to show that for increments of 1 year the increments of the salary is $500:
Year Salary Change in year Change in salary
2010 A - -
2011 A + 500 2011 - 2010 = 1 A + 500 - 500 = 500
2012 A + 1,000 2012 - 2011 = 1 A + 1,000 - (A + 500) = 500
So, you can see that every year the salary increases the same amount ($500).
In general, a linear model is represented by the general equation y = mx + b, where x is the change of y per unit change of x, and b is the initial value (y-intercept).
In this case, m = $500 and b is the starting salary: y = 500x + b.
The table below represents the function F. 3 7 F(x) 4 15 5 31 7 127 8 255 The equation that represents this function is?
Answers
The table is an exponential function, and the equation that represents this function is \(f(x) =2^x -1\)
The equation of the tableThe table is given as:
x F(x)
4 15
5 31
7 127
8 255
Rewrite the table as:
x F(x)
4 16 - 1
5 32 - 1
7 128 - 1
8 256 - 1
Express as a base of 2
x F(x)
4 2⁴ - 1
5 2⁵- 1
7 2⁷ - 1
8 2⁸ - 1
Notice that the function is 1 subtracted from 2 raised to the power of the input.
This is represented as:
\(f(x) =2^x -1\)
Hence, the equation of the table is \(f(x) =2^x -1\)
Read more about exponential functions at
https://brainly.com/question/9608962
#SPJ1
The height of a rocket a given number of seconds after it is released is modeled by h(t)=-16t+32t+10 what does t represent?
Answers
The graph to the right is the uniform probability density function for a friend who is x minutes late. (a) Find the probability that the friend is between 10 and 30 minutes late. (b) It is 10 A.M. There is a 20% probability the friend will arrive within how many minutes? part a) what is the probability that the friend is between 10 and 30 minutes late_?

Answers
The probability that the friend is between 10 and 30 minutes late is approximately 0.6667, or 66.67%.
Since the probability density function is uniform, the probability of the friend being between 10 and 30 minutes late is equal to the area of the rectangle that lies between x = 10 and x = 30, and below the curve of the probability density function.
The height of the rectangle is equal to the maximum value of the probability density function, which is 1/30 since the interval of possible values for x is [0, 30] minutes.
The width of the rectangle is equal to the difference between the upper and lower limits of the interval, which is 30 - 10 = 20 minutes.
Therefore, the probability of the friend being between 10 and 30 minutes late is:
P(10 < x < 30) = (height of rectangle) x (width of rectangle)
= (1/30) x 20
= 2/3
≈ 0.6667
So the probability that the friend is between 10 and 30 minutes late is approximately 0.6667, or 66.67%.
To know more about probability follow
https://brainly.com/question/27077702
#SPJ1
a certain forest covers 4400 km^2 suppose that each year this area decreases by 7.25% what will the area be after 6 years?
Answers
In accordance with the exponential model, the current forest area is equal to 2801.149 square kilometers after six years.
What forest area shall remain after 6 years?
According with statement, the forest area decreases exponentially in time. Then, the exponential model is defined by following model:
n(x) = n' · (1 - r)ˣ
Where:
n' - Initial forest area, in square kilometers.r - Grown rate.x - Time, in years.If we know that n' = 4400 km², r = 0.0725 and x = 6 yr, then the current forest area is:
n(6) = 4400 · (1 - 0.0725)⁶
n(6) = 2801.149
To learn more on exponential functions: https://brainly.com/question/30951187
#SPJ1
Find the mean, median, mode and range of the following data
set:
13, 2, 20, 20, 14, 16, 20, 30, 3, 40
Answers
Answer:↓↓
Step-by-step explanation:
2, 3, 13, 14, 16, 20, 20, 20, 30, 40
Mean: the average of a data set.
2 + 3 + 13 + 14 + 16 + 20 + 20 + 20 + 30 + 40 / 10 = 178/10 = 17.8
Median: the middle of the set of numbers.
16 + 20 / 2 = 36/2 = 18
Mode: the most common number in a data set.
20
Range: The difference of the smallest and highest number.
40 - 2 = 38
Assume that in a given year the mean mathematics SAT score was 515, and the standard deviation was 116. A sample of 65 scores is chosen. Use the TI-84 Plus calculator. Part 1 of 5 (a) What is the probability that the sample mean score is less than 500
Answers
Answer:
His is a normal distribution question with a) x1 = 480 x2 = 520 P(480.0 < x < 520.0)=? This implies that P(480.0 < x < 520.0) = P(-2.4326 < z < 0.3475) = P(Z < 0.3475) - P(Z < -2.4326)
Step-by-step explanation:
A Sample Of 65 Scores Is Chosen. Use The TI-84 Plus Calculator. Part 1 Of 5 (a) What Is The Probability That The Sample Mean Score Is Less Than 5007
H . E . L . P
this work is due tomorrow, and i have absolutely no idea what the answer is. please help me.
DONT COMMENT FOR POINTS PLEASE

Answers
Answer:
A) 5
B) 20
C) 28
D) 25
Step-by-step explanation:
Hope this helps :))
Answer:
a) a-b
7-2 =5
b) 2×a + 3×b
2×7 + 3×2
14 +6 =20
c) 2ab
2×a×b
2×7×2 =28
d) (7-2) power of 2
5 power of 2
5+5 =10
Two angles form a linear pair, the sum of one angle plus 27 is equal to two times the sum of the other angle
Answers
The pair of Linear angles are 51° and 129°.
What are Linear Angles:When two lines intersect at a point then they will form two linear angles. The sum of angles of a linear pair is always equal to 180°. Such angles are also known as supplementary angles.
In other words, if the sum of two adjacent angles is 180° then the pair of angles are said to be Linear Angles.
Here we have
Two angles form linear angles
Let x and y be the two angles
=> x + y = 180 ------ (1) [ since both are linear angles ]
Given that the sum of one angle plus 27 is equal to two times the sum of the other angle
=> x + 27 = 2y
=> x = (2y - 27) ---- (2)
Substitute (2) in (1)
=> 2y - 27 + y = 180
=> 3y = 153
=> y = 153/3
=> y = 51
Now substitute y = 51 in (1)
=> x + 51 = 180
=> x = 180 - 51
=> x = 129
The pair of Linear angles are 51° and 129°.
Learn more about Linear Angles at
https://brainly.com/question/26555759
#SPJ1