A college plans to interview 8 students for possible offer of graduate assistantships. The college has three assistantships available. How many groups of three can the college select?.
Answers
The number of groups of three that the college can select is 56.
Total number of students = 8
Number of assistantships available = 3
Groups of three can be selected by the college means that out of the eight students three need to be selected at random and this can be done in ⁸\(C_{3}\) ways.
In this case, we use combination and not permutation because the order of selection of the students does not matter.
Now, we know
ⁿ\(C_{r}\) = ( n! )/( r! (n-r )!)
Here, n = 8 and r = 3
⁸\(C_{3}\) = ( 8! )/( 3! (8-3)! )
⁸\(C_{3}\) = ( 8 × 7 × 6 × 5! )/ ( 3 × 2 × 1 × ( 5! ) )
⁸\(C_{3}\) = ( 8 × 7 × 6 )/ ( 3 × 2 )
⁸\(C_{3}\) = 56
The number of groups of three that the college can select is 56.
To know more about Combination and Permutation Refer to the link:
https://brainly.com/question/11732255
#SPJ4
Related Questions
If the sum of an infinite geometric series is \( \frac{15625}{24} \) and the common ratio is \( \frac{1}{25} \), determine the first term. Select one: a. 625 b. 3125 c. 25 d. 125
Answers
The first term of the infinite geometric series is 625.Let's dive deeper into the explanation.
We are given that the sum of the infinite geometric series is \(\( \frac{15625}{24} \)\)and the common ratio is\(\( \frac{1}{25} \).\)The formula for the sum of an infinite geometric series is \(\( S = \frac{a}{1 - r} \)\), where \( a \) is the first term and \( r \) is the common ratio.
Substituting the given values into the formula, we have \(\( \frac{15625}{24} = \frac{a}{1 - \frac{1}{25}} \).\)To find the value of \( a \), we need to isolate it on one side of the equation.
To do this, we can simplify the denominator on the right-hand side.\(\( 1 - \frac{1}{25} = \frac{25}{25} - \frac{1}{25} = \frac{24}{25} \).\)
Now, we have \(\( \frac{15625}{24} = \frac{a}{\frac{24}{25}} \).\) To divide by a fraction, we multiply by its reciprocal. So, we can rewrite the equation as \( \frac{15625}{24} \times\(\frac{25}{24} = a \).\)
Simplifying the right-hand side of the equation, we get \(\( \frac{625}{1} = a \).\)Therefore, the first term of the infinite geometric series is 625.
In conclusion, the first term of the given infinite geometric series is 625, which corresponds to option (a).
learn more about geometric series here here
https://brainly.com/question/30264021
#SPJ11
what is the cosine form of the function 10sin(wt 40)
Answers
The cosine form of the function 10sin(wt - 40) is 10cos(wt - 50).
The cosine form of the function 10sin(wt - 40) can be found using the identity sin(x - y) = sin(x)cos(y) - cos(x)sin(y).
By applying this identity to the given function, we can rewrite it in terms of cosine.
10sin(wt - 40) = 10(sin(wt)cos(40) - cos(wt)sin(40))
Now, we can use the fact that cos(90 - x) = sin(x) and sin(90 - x) = cos(x) to further simplify the expression.
10(sin(wt)cos(40) - cos(wt)sin(40)) = 10(sin(wt)sin(50) + cos(wt)cos(50))
Finally, we can use the identity cos(x + y) = cos(x)cos(y) - sin(x)sin(y) to rewrite the expression in terms of cosine.
10(sin(wt)sin(50) + cos(wt)cos(50)) = 10cos(wt - 50)
Therefore, the cosine form of the function 10sin(wt - 40) is 10cos(wt - 50).
To know more about cosine form click on below link:
https://brainly.com/question/3516247#
#SPJ11
At a road work site, 20 cones are placed along 50 feet of road. How many cones are placed along 35 feet of road?
Answers
Answer: 14 cones
Step-by-step explanation:
We can do 50/20
= 2.5 cones placed per feet of distance (vector)
To find: How many cones are placed along 35 feet of road?
We can now divide 35 by 2.5 and the result is 14.
14 cones were placed, in the interval of 35 feet.
Answer: 14
Step-by-step explanation: if we divide the total length by the amount of cones we get 2.5 which is feet between cones, so now we start with 2.5 = 1 and get 2.5 to 35 so the 1 is the answer, finally dividing 35 by 2.5 gives us the answer: 14.
Find the product of the complex numbers. express your answer in trigonometric form.
Answers
The product of the complex numbers in trigonometric form computed as:
\(\(z_1 \cdot z_2 = r_1 r_2 (\cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2))\)\)
To find the product of two complex numbers in trigonometric form, we can multiply their magnitudes and add their arguments. Let's denote the complex numbers as follows:
Number 1: \(\(z_1 = r_1(\cos \theta_1 + i \sin \theta_1)\)\)
Number 2: \(\(z_2 = r_2(\cos \theta_2 + i \sin \theta_2)\)\)
The product of these complex numbers can be computed as:
\(\(z_1 \cdot z_2 = r_1 r_2 (\cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2))\)\)
In this form, \(\(r_1\) and \(r_2\)\) represent the magnitudes of the complex numbers, and \(\(\theta_1\) and \(\theta_2\)\) represent their arguments.
Please provide the values of the complex numbers you want to multiply, and I'll calculate their product in trigonometric form for you.
Learn more about complex numbers here:
https://brainly.com/question/20566728
#SPJ11
An equation is modeled. What value of x makes the equation true?
Answers
An equation is modeled. The value of x makes the equation true is -1.
Equation:
Conditional comparisons apply only to specific values of variables. An equation consists of two expressions joined by an equal sign ("="). Expressions for both sides of the equals sign are called the "left side" and the "right side" of the equation. Usually the right side of the equation is assumed to be zero. If this is accepted, it does not reduce the generality, since it can be done by subtracting the right side from the two sides.
According to the Question:
5x + 6 = 1
5x = -5
x = -1
Complete Question:
An equation is modeled. What value of x makes the equation true?
(1) 1
(2) 7
(3) -5
(4) -1
Learn more about Equation:
https://brainly.com/question/29657983
#SPJ4

Please help me please please please please please help me I’ll give brainly

Answers
Answer:
3y
Step-by-step explanation:
Divide the numbers and then divide the variables.
21/7 = 3
y²/y = y
Therefore,
21y²/7y = 3y
plsss help i’ll give brainliest if you give a correct answer

Answers
Answer:
x = 23
Step-by-step explanation:
I hope this helps! Have a good day! :)
Will 10 + x to the second power be greater than 2 to the x power
Answers
\(10 + x^2\) Will be greater than \(2^x\)for certain values of x, specifically when x is approximately less than
0.543 and between 4.337 and 5.172.
Set up the inequality: \(10 + x^2 > 2^x\)
Since there's no algebraic method to solve this inequality directly, we can analyze it graphically.
Plot the two functions,\(y1 = 10 + x^2\) and\(y2 = 2^x\), on a graph.
Find the points where the two graphs intersect.
If there's a region where the graph of y_1 is above the graph of y_2, that means \(10 + x^2 > 2^x\) in that region.
When analyzing the graphs, you'll find that\(10 + x^2 > 2^x\) for x approximately less than 0.543 and x approximately
between 4.337 and 5.172.
In these regions, the inequality holds true.
In conclusion, \(10 + x^2\) will be greater than \(2^x\) for certain values of x, specifically when x is approximately less than 0.543 and between 4.337 and 5.172.
for such more questions on inequality
https://brainly.com/question/30238989
#SPJ11
What can you observe in the graph of a logarithmic function?.
Answers
The logarithmic function is inverse of expontial function that why graph of logarithmic function is draw according to features of expontial function.
The logarithmic function \( f(x) = log_{b}(x) \) is the inverse of the exponential function y=bˣ. Clearly, the logarithm function must have domains and limits of (0, ∞) and (−∞,∞). The logarithmic function can be graphed by examining the graph of the exponential function and swapping x and y. Graphs of exponential functions f (x) = bˣ or y = bˣ include the following features:
The domain of exponential is real (-∞,∞). The range is also a positive real number (0, ∞).The graph of an exponential function usually passes through the point (0, 1). This means that the y-intersection is at pt. (0, 1).The graph of the exponential function f(x) =bˣ has a horizontal asymptote at y = 0.Exponential graphs decrease from left to right when 0 < b < 1, in which case they are called exponential decays.If the basis of a function f(x) = bˣ , b> 1, its graph grows from left to right and is called exponential growth.For example, the graph above represents a logarithmic function, \( f(x) = log_{2}(x) \).
To learn more about Logarithm function, refer:
https://brainly.com/question/30283912
#SPJ4

Lawrence, an attorney, charges an initial fee of $100 plus $75 per hour for a consultation. he typically charges clients either less than $250 or more than $700. which inequality represents x, the typical number of hours worked? 75x 100 < 250 or 75x 100 > 700 100x 75 < 250 or 100x 75 > 700 250 < 75x 100 < 700 250 < 100x 75 < 700
Answers
The inequality that represents the typical number of hours worked, x, is 250 < 75x + 100 < 700.
To determine the inequality that represents the typical number of hours worked, we need to consider the given information about Lawrence's charges and the range of fees he typically charges clients.
We know that Lawrence charges an initial fee of $100, which is a fixed cost regardless of the number of hours worked. Additionally, he charges $75 per hour for a consultation. Therefore, the total cost for a consultation can be represented as $75x, where x is the number of hours worked.
Now, let's consider the range of fees Lawrence typically charges clients. It is mentioned that he charges either less than $250 or more than $700. This means that the total cost of a consultation, which includes the initial fee and the hourly rate, must be either less than $250 or more than $700.
Combining these conditions, we can write the inequality:
250 < (75x + 100) < 700
This inequality states that the total cost of a consultation (75x + 100) must be greater than $250 and less than $700. Therefore, it represents the typical number of hours worked, x, for Lawrence.
To learn more about inequality visit : https://brainly.com/question/30238989
#SPJ11
I need help on this

Answers
Answer:
I think that it is A or D
Step-by-step explanation:
Graph the linear equation
5x - y = 30 by following these steps:
Step 1: Find the x-intercept. Let y = 0 and solve for x.
=
Answers
Answer:
Step-by-step explanation:
5x-(0)=30
add 0 to both sides to cancel
5x=30
divide by 5 on both sides to cancel
x=6
Which number line have a point that is equal to point p? Check all that apply
Answers
A and C is the answer
Answer: A and C
Step-by-step explanation:
I would really appreciate some help with identifying the language needed to solve this in a program like STATA. I need to learn how to write in a enonometrics related program in order to solve problems based on data from the book's website. thank you
http://wps.aw.com/aw_stock_ie_3/178/45691/11696965.cw/index.html
Additional Empirical Exercise 4.3
The data file CollegeDistance contains data from a random sample of high school seniors interviewed in 1980 and re-interviewed in 1986. In this exercise, you will use these data to investigate the relationship between the number of completed years of education for young adults and the distance from each student’s high school to the nearest four-year college. (Proximity to college lowers the cost of education, so that students who live closer to a four-year college should, on average, complete more years of higher education.)
A detailed description is given in College Distance_Description, also available on the Web site.1
a. Run a regression of years of completed education (ED) on distance to the nearest college (Dist), where Dist is measured in tens of miles. (For example, Dist = 2 means that the distance is 20 miles.) What is the estimated intercept? What is the estimated slope? Use the estimated regression to answer this question: How does the average value of years of completed schooling change when colleges are built close to where students go to high school?
b. Bob’s high school was 20 miles from the nearest college. Predict Bob’s years of completed education using the estimated regression. How would the prediction change if Bob lived 10 miles from the nearest college?
c. Does distance to college explain a large fraction of the variance in educational attainment across individuals? Explain.
d. What is the value of the standard error of the regression? What are the units for the standard error (meters, grams, years, dollars, cents, or something else)?
Answers
The given empirical exercise aims to investigate the relationship between the number of completed years of education and the distance from high schools to the nearest four-year college. To address this, the STATA programming language can be used.
Running a regression of completed education (ED) on distance to the nearest college (Dist) provides insights into this relationship. The estimated intercept represents the average number of completed years of schooling when the distance to the nearest college is zero, while the estimated slope indicates the average change in completed education associated with a one-unit increase in distance. This allows us to understand the effect of college proximity on average educational attainment.
By predicting Bob's completed education using the estimated regression, we can assess the impact of distance on his educational attainment. Altering the distance value in the prediction allows us to observe how the regression equation affects the predicted education level for Bob.
The R-squared value measures the proportion of variance in educational attainment explained by distance to college. A higher R-squared value suggests that distance to college explains a larger fraction of the differences in educational attainment among individuals.The standard error of the regression, expressed in years, represents the average deviation between observed and predicted years of completed education. It provides information about the precision of the regression estimates.
To learn more about regression click here brainly.com/question/28178214
#SPJ11
An isosceles triangle had two base angles equal to 13 degrees. What is the measure of the third angle?
Answers
The measure of the third angle of the isosceles triangle is θ = 154°
Given data ,
In an isosceles triangle, two sides are of equal length, and thus two base angles are also of equal measure.
Given that the two base angles of the isosceles triangle are both 13 degrees, we can denote one of the base angles as 13 degrees, and the other base angle as 13 degrees as well.
Let's denote the measure of the third angle as "x" degrees
The sum of angles in any triangle is always 180 degrees.
So , 13 + 13 + x = 180
Simplifying the equation:
26 + x = 180
Subtracting 26 from both sides of the equation:
x = 180 - 26
x = 154°
Hence , the measure of the third angle in the isosceles triangle is 154°
To learn more about isosceles triangle click :
https://brainly.com/question/1900674
#SPJ1
Jeffrey went to the movies with his friends. The tickets cost $8.50 each for students and they spent $15.00 altogether at the concession stand. Their total was $49.00. How many people went to the movies?
Answers
Answer:
4 people
Step-by-step explanation:
Let's first write an equation.
We want to find the number of tickets t
The total was $49 so our equation will equal $49 and they spent $15 in snacks so on the other side of the eqaution we have to add $15, on the same side as the snacks we need to add in the cost of tickets, which is $8.50 multiplies by t, or the total number of tickets.
$49 = $8.50t + $15
Solve for t, first subtract $15 from both sides.
$49 - $15 = $8.50t
$34 = $8.50t Divide both sides by $8.50
$34/$8.50 = $8.50t/$8.50
$34/$8.50 = t
4 = t
4 tickets meaning 4 people went.
Find the difference between points M(6, 16) and Z(-1, 14) to the nearest tenth.
Answers
The distance between points M(6, 16) and Z(-1, 14) is approximately 7.1 units.
We can use the distance formula to find the distance between two points in a coordinate plane. The distance formula is:
d = √((x2 - x1)² + (y2 - y1)²)
where (x1, y1) and (x2, y2) are the coordinates of the two points. Substituting the coordinates of M(6, 16) and Z(-1, 14), we get:
d = √((-1 - 6)² + (14 - 16)²) = √(49 + 4) = √53 ≈ 7.1
Therefore, the distance between points M(6, 16) and Z(-1, 14) is approximately 7.1 units.
To learn more about
nearest tenth
brainly.com/question/12102731
#SPJ11
45/27=x/3 solve for x pls help
Answers
Answer:
x = 5
Step-by-step explanation:
hope this helps!!
Answer:
x=5
Step-by-step explanation:
5/3=45/27

You created a new playlist, 100 of your freinds listen to it and shared if they liked the new playlist or not. Rachel said the ratio of the number of the people who liked the playlist to the number of people who did not like the playlist is 75:25. Dylan said that for every three people who liked the playlist, one person did not. Do Rachel and Dylan argree? Prove your answer using the values of the ratio.
Answers
Answer:
- Yes, They agree
Step-by-step explanation:
Do Rachel and Dylan argree?
- Yes, They agree
Prove your answer using the values of the ratio.
100 of your friends listen to it
- Total Number = 100
Rachel said the ratio of the number of the people who liked the playlist to the number of people who did not like the playlist is 75:25.
The ratio can be simplifies further by diving all through by 25;
75/25 : 25/25
3 : 1
Dylan said that for every three people who liked the playlist, one person did not.
This simplifies to 3 : 1.
Same thing with what rachel said, so they both agree
The mapping diagram shows a functional relationship. A mapping diagram shows a relation, using arrows, between domain and range for the following ordered pairs: (8, 4), (negative two-thirds, 3), (11, negative 1), (4, one-half). Complete the statements. f(4) is . f(x) = 4 when x is?
Answers
Answer:
f(4) is 1/2 the second is 8
Step-by-step explanation:
Answer:
1: 1/2
2: 8
Step-by-step explanation:
I did the assignment
First gets brainliest and i can solve any question you have :D



Answers
First is $677.5
Second is 2.8%
Third is increase, decrease, and increase i believe
Describe the translation from the pre-image to the image please

Answers
Step-by-step explanation:
Look at point A ====> A'
x goes from 1 to 4 so X: x + 3
y goes from 7 to 3 so Y: y - 4
10
이
10
4
Which of the following are integers
Answers
Integers consists of positive whole numbers and their negative opposites and zero. |0| is equal to 0 which also makes it an integer.
Write the quadratic function f(x) = x2 + 8x + 3 in vertex form.
Answers
The length of two sides of a triangle are 4 units and 7 units. The length of the third side is a whole number of units. What is the maximum possible length of the third side?
Answers
Answer:
I think you have to calculate the length and the units like 4+7 and then × it
A power outage affected all homes and businesses within a 5 mi radius of the power station. If the power station is located 1 mi west and 3 mi north of the center of town, find an equation of the circle consisting of the furthest points from the station affected by the power outage.
Answers
Answer: x^2 - 2x + y^2 - 6y + 10 = 0.
Step-by-step explanation: The power station is located 1 mi west and 3 mi north of the center of town, which means that it is located at the point (1, 3) on the coordinate plane. The power outage affected all homes and businesses within a 5 mi radius of the power station, which means that the furthest points from the station affected by the power outage are located on a circle with a radius of 5 mi.
The equation of a circle with center (h, k) and radius r is given by:
(x - h)^2 + (y - k)^2 = r^2
Substituting the values for the center of the circle (h, k) = (1, 3) and the radius r = 5, the equation of the circle consisting of the furthest points from the power station affected by the power outage is:
(x - 1)^2 + (y - 3)^2 = 5^2
This simplifies to:
x^2 - 2x + 1 + y^2 - 6y + 9 = 25
Combining like terms, the equation becomes:
x^2 - 2x + y^2 - 6y + 10 = 0
This can be written in standard form as:
x^2 - 2x + y^2 - 6y + 10 = 0
Therefore, the equation of the circle consisting of the furthest points from the power station affected by the power outage is x^2 - 2x + y^2 - 6y + 10 = 0.
the length of a rectangle is six more than double the width. if the perimeter is 90 inches, find the dimensions.
Answers
The dimensions of the rectangle are a width of 13 inches and a length of 32 inches.
To find the dimensions of the rectangle with a perimeter of 90 inches, follow these steps:
Let the width of the rectangle be represented as w.
Since the length is six more than double the width, we can represent the length as 2w + 6.
The formula for the perimeter of a rectangle is P = 2L + 2W, where P is the perimeter, L is the length, and W is the width.
Substitute the given perimeter (90 inches) and the expressions for length and width into the formula: 90 = 2(2w + 6) + 2w.
Simplify the equation: 90 = 4w + 12 + 2w.
Combine the terms with w: 90 = 6w + 12.
Subtract 12 from both sides of the equation: 78 = 6w.
Divide both sides by 6 to solve for w: w = 13.
Substitute the value of w back into the expression for the length: L = 2(13) + 6 = 26 + 6 = 32.
The rectangle is a size of 13 inches in width and 32 inches in length.
Learn more about "Rectangle perimeter": https://brainly.com/question/19819849
#SPJ11
find the value of k, so that the difference of roots of x^2_5x + 3{k_1} =0 is 11
Answers
u can find the answer in the attached file

To convert 120 ounces to pounds, which of the following proportions should you use?
ANSWER VERY QUICKLY PLEASE!!!! NEED ANSWERS ASAP.
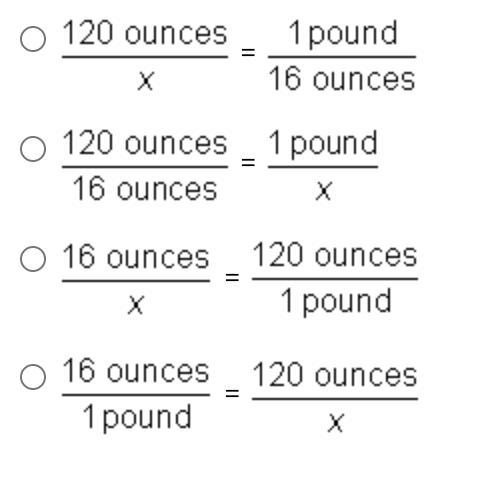
Answers
Answer: you would use the last option
4. 9d - 5 = 4
What does d =
5. 6-3w=-27 what does w =
6. -4= q/8-19 what does q =
Answers
Answer:
4) d = 1
5) w = 11
6) q = 120
Step-by-step explanation:
4) \(9d - 5 = 4\)
Adding 5 on both the sides ,
\( = > 9d - 5 + 5 = 4 + 5\)
\( = > 9d = 9\)
Dividing both the sides by 9 ,
\( = > \frac{9d}{9} = \frac{9}{9} \)
\( = > d = 1\)
5) \(6 - 3w = - 27\)
Substracting 6 from both the sides ,
\(6 - 3w - 6 = - 27 - 6\)
\( = > - 3w = - 33\)
Dividing both the sides by -3 ,
\( = > \frac{ - 3w}{ - 3} = \frac{ - 33}{ - 3} \)
\( = > w = 11\)
6) \( - 4 = \frac{q}{8} - 19\)
Adding 19 on both the sides ,
\( \frac{q}{8} - 19 + 19 = - 4 + 19\)
\( = > \frac{q}{8} = 15\)
Multiplying both the sides by 8 ,
\( = > \frac{q}{8} \times 8 = 15 \times 8\)
\( = > q = 120\)