a cheeta runs a speed of 65mi/hr, how many meters/second is that?
Answers
Answer: 29.058
Step-by-step explanation:N/A
Related Questions
Can somebody help me?

Answers
Just believe me thats the correct answer
Which figure best represents a kite?
A figure with 1 pair of parallel sides.
A figure with 2 pairs of parallel sides with the different lengths.
A square.
A kite.
Answers
Which side of triangle XYZ is the longest?
A. overline XY
B. overline XZ
C. overline YZ
D. Cannot be determine
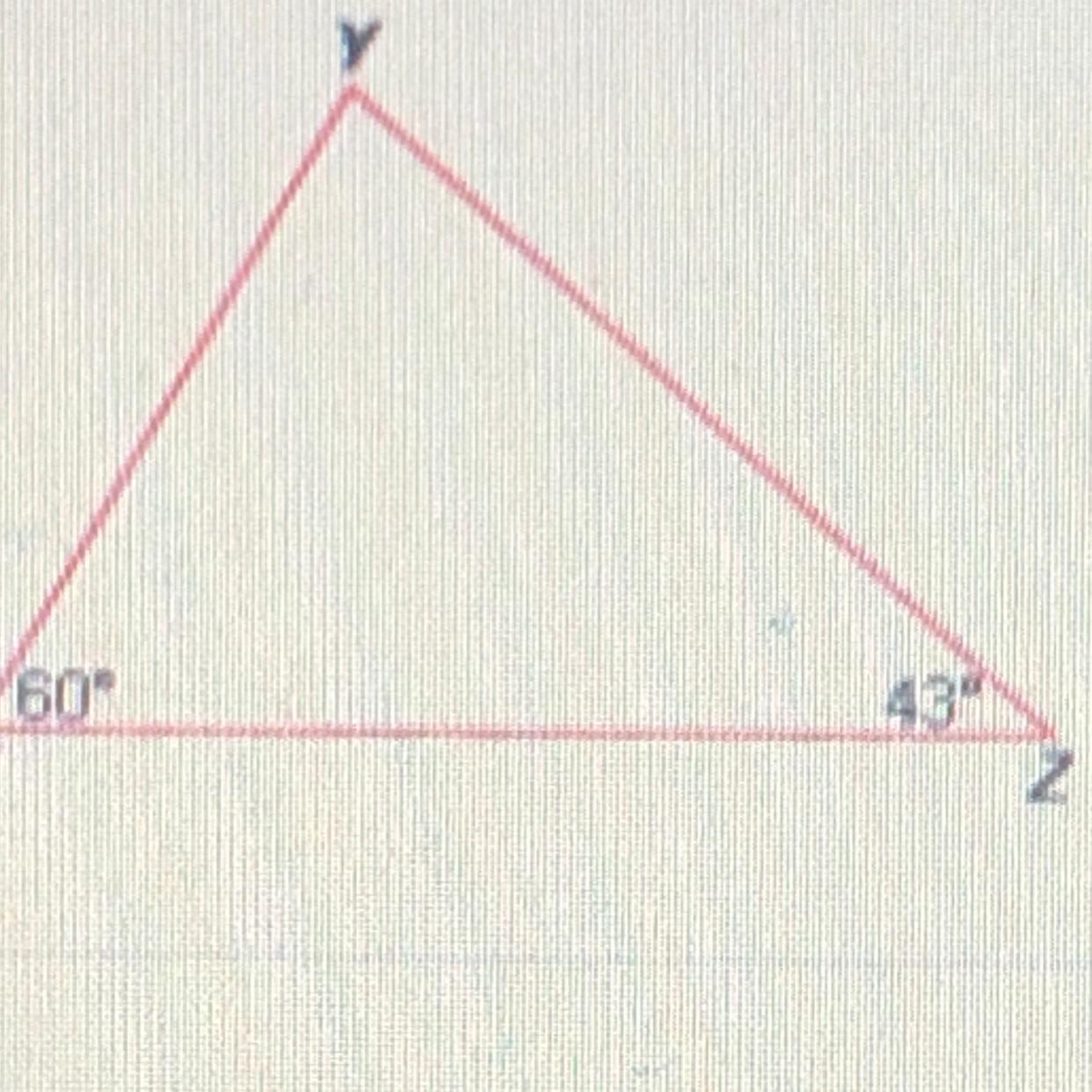
Answers
Answer:
B)XZ
Used a calculator and just took this quiz
Answer:
B
Step-by-step explanation:
m < y = 180 degrees - 60 degrees - 43 degrees = 77 degrees
77 > 60 > 43
xz > yz > xy
XZ is the longest side. So the answer is B
2+2= what +6 HA they cant repo this so u guys can get points
Answers
Answer:
10
Step-by-step explanation:
2+2=4
4+6= 10
Answer:
The answer is uhhhhhhhh 10
Step-by-step explanation:
a carpenter has three sheets of plywood that are each 6.85 feet long. a 3.4-foot piece is cut from one sheet 0.5-foot piece is cut from another piece. How many feet in plywood is left in all
Answers
Answer:
16.65 feet
Step-by-step explanation:
Okay, we have three boards that are each 6.85 feet long. If we cut 3.4 feet off one board, that board has:
6.85
−
3.4
=
3.45
feet left
If we cut off 0.5 feet off another board, that board has:
6.85
−
0.5
=
6.35
feet left
So, if we take our three new boards, the total length of plywood left is:
6.85
+
3.45
+
6.35
=
16.65
feet
Hope this helps!
a tank is 3/7 full of water.After removing 420 litres it became 12/35 full .how much can the tank hold when full?
Answers
Answer:
4900 Litres
Step-by-step explanation:
First we need a common demoninator:
3/7=15/35
Then we subtract the two to figure out how much 420 Litres is:
15/35-12/35=3/35
3/35=420 litres
Divide amount by the numerater for thow much 1/x is.
1/35=140
and multiply by the denomenator to get a full number on your fraction, and therefore a full tank.
140 x 35 = 4900
show that acos(wt)+bsin(wt) can be written in the form
Answers
This form of the equation is useful because it shows that any periodic function of time can be represented as a sum of sine and cosine functions with different amplitudes and phases.
We can show that acos(wt) + bsin(wt) can be written in the form Rsin(wt + φ) where R and φ are constants and R is the amplitude of the wave.
Using the trigonometric identity sin(a+b) = sin(a)cos(b) + cos(a)sin(b), we can write:
acos(wt) + bsin(wt) = R(sin(wt+φ)),
where R = √(a^2+b^2) and φ = tan⁻¹(b/a).
To see how this works, we can use the values of a = 3 and b = 4 as an example:
acos(wt) + bsin(wt) = 3cos(wt) + 4sin(wt)
R = √(a^2+b^2) = √(3^2 + 4^2) = 5
φ = tan⁻¹(b/a) = tan⁻¹(4/3)
So we can rewrite the equation as:
acos(wt) + bsin(wt) = 5sin(wt + tan⁻¹(4/3))
This form of the equation is useful because it shows that any periodic function of time can be represented as a sum of sine and cosine functions with different amplitudes and phases. It is also helpful in analyzing the properties of waves, such as their amplitude and frequency.
Learn more about periodic function here
https://brainly.com/question/29120892
#SPJ11
6-5 Practice Operations with radical expressions
1. √540
2. 3√432
3. 3√128
4. - 4√405
5. 3√-5000
Answers
The Practice Operations with radical expressions is simplified using the basic of the Algebra:
Algebraic expressions incorporating radicals are known as radical expressions. The root of an algebraic expression makes up the radical expressions (number, variables, or combination of both). The root might be an nth root, a square root, or a cube root. Radical expressions can be made simpler by taking them down to their most basic form and, if feasible, getting rid of all of the radicals.
Radical expressions are simplified by taking them down to their most basic form and, if feasible, altogether deleting the radical. An algebraic expression's numerator and denominator are multiplied by the appropriate radical expression if the denominator contains a radical expression.
Practice Operations with radical expressions are:
1) \(\sqrt{540}\) = \(\sqrt{36 * 15 }\)
= 6√15
2) \(\sqrt[3]{432}\) = \(\sqrt[3]{216*2}\)
= \(6\sqrt[3]{2}\)
3) \(\sqrt[3]{128}\) = \(\sqrt[3]{64*2}\)
= \(4\sqrt[3]{2}\)
4) \(-\sqrt[4]{405}\) = \(-\sqrt[4]{81*5}\)
= \(-3\sqrt[4]{5}\)
5) \(\sqrt[3]{-5000}\) = \(-\sqrt[3]{1000*5}\)
= \(-10\sqrt[3]{5}\)
Learn more about Radical expressions:
https://brainly.com/question/26637176
#SPJ4
URGENT PLEASE HELP!!! WILL GIVE 20 POINTS
Read this excerpt from Infinite Jest.
'I could, if you'd let me, talk and talk. Let's talk about anything. I believe the influence of Kierkegaard on Camus is
underestimated. I believe Dennis Gabor may very well have been the Antichrist. I believe Hobbes is just
Rousseau in a dark mirror. I believe, with Hegel, that transcendence is absorption. I could interface you guys
right under the table,'I say. “I'm not just a creâtus, manufactured, conditioned, bred for a function.'
What assumption does the narrator make in this excerpt?
that the people he is addressing enjoy long conversations
O that the people he is addressing appreciate intellectualism
that the people he is addressing have researched philosophy
that the people he is addressing expect a confrontation
Answers
Answer: that the people he is addressing appreciate intellectualism
Step-by-step explanation: found it on quizlet
Answer:
That the people he is addressing have researched philosophy
Step-by-step explanation:
i said so
Yooooo somebody help me with this.

Answers
Answer
one line is points (-9,4 ) (1,-2) and both cross over each at (3,4)
Step-by-step explanation:
Honors algebra was a tragic year
(0)
A production line operates for two eight-hour shifts each day. During this time, the production line is expected to produce 3,000 boxes. What is the takt time in minutes?
Group of answer choices
.25
.3
3
.6
Answers
The expected number of boxes to be produced is given as 3,000 boxes. So, the correct answer is 0.3, indicating that the takt time in minutes is 0.3 minutes.
The production line operates for two eight-hour shifts each day, which means there are 16 hours of production time available. Since there are 60 minutes in an hour, the total available time in minutes would be 16 hours multiplied by 60 minutes, which equals 960 minutes.
The expected number of boxes to be produced is given as 3,000 boxes.
To calculate the takt time in minutes, we divide the total available time (960 minutes) by the expected number of boxes (3,000 boxes):
\(Takt time = Total available time / Expected number of boxes\)
\(Takt time = 960 / 3,000\)
By performing the calculation, we find that the takt time is approximately 0.32 minutes, which is equivalent to 0.3 minutes rounded to one decimal place.
Learn more about minutes here:
https://brainly.com/question/31148642
#SPJ11
mary and jerry are excercising on a track. mary is walking a rate of 3 miles per hour. Jerry starts jogging at a rate of 4 miles per hour after mary has been walking for 15 minutes. Jerry jogs 2 miles as mry continues walking, they both stop at the same time. what is the total distance in miles that mary walks around the track
Answers
The total distance covered by Mary while walking around the track is 2 1/2 miles.
On a track, Mary and Jerry are working out.
Mary is moving along at a 3 mph pace.
After Mary has been walking for fifteen minutes, Jerry begins to jog at a speed of four miles per hour.
Mary continues to walk as Jerry jogs for two kilometers before they both stop at the same time.
Enter Mary's total walking mileage around the track in miles.
Find the distance M had walked when J starts jogging.
15 min = 0.25 hrs
3 × .25 = .75 miles
Find how long it took J to jog 2 miles at 4 mph
2/4 = .5 hrs
Find how far M can walk in .5 hrs at 3 mph
.5 × 3 = 1.5 miles
Enter the total distance, in miles, that Mary walks around the track
.75 + 1.5 = 2.25 mi or 2 1/4 miles.
Hence distance covered in miles is 2.25 miles.
Learn more about Speed distance and time here:
brainly.com/question/7243416
#SPJ1
Can a triangle be made from 24cm,8cm,30cm
Answers
explanation: all triangles have to equal 180 degrees. this triangle equals 62 degrees.
because if 24 cm and 8 cm are sides A and B then a squared plus b squared should equal to to a little more than c squared.
For the following right triangle, find the side length x. Round your answer to the nearest hundredth.
8
14
X
Answers
So, we have:
8^2 + 14^2 = x^2
Simplifying:
64 + 196 = x^2
260 = x^2
Taking the square root of both sides:
x = 16.12
So, the length of the hypotenuse is approximately 16.12.
My math grade went from a 78 to a 86. What is the percent increase
Answers
Answer:
10.25641...% or 10.3%
Step-by-step explanation:
(86/78)/78 = 8/78
8/78 * 100 = 400/39 = 10.25641...%
Students arrive at the Administrative Services Office at an average of one every 12 minutes, and their requests take on average 10 minutes to be processed. The service counter is staffed by only one clerk, Judy Gumshoes, who works eight hours per day. Assume Poisson arrivals and exponential service times. Required: (a) What percentage of time is Judy idle? (Round your answer to 2 decimal places. Omit the "%" sign in your response.) (b) How much time, on average, does a student spend waiting in line? (Round your answer to the nearest whole number.) (c) How long is the (waiting) line on average? (Round your answer to 2 decimal places.) (d) What is the probability that an arriving student (just before entering the Administrative Services Office) will find at least one other student waiting in line? (Round your answer to 3 decimal places.)
Answers
The probability that an arriving student will find at least one other student waiting in line is approximately 0.167.
To solve this problem, we'll use the M/M/1 queueing model with Poisson arrivals and exponential service times. Let's calculate the required values: (a) Percentage of time Judy is idle: The utilization of the system (ρ) is the ratio of the average service time to the average interarrival time. In this case, the average service time is 10 minutes, and the average interarrival time is 12 minutes. Utilization (ρ) = Average service time / Average interarrival time = 10 / 12 = 5/6 ≈ 0.8333
The percentage of time Judy is idle is given by (1 - ρ) multiplied by 100: Idle percentage = (1 - 0.8333) * 100 ≈ 16.67%. Therefore, Judy is idle approximately 16.67% of the time. (b) Average waiting time for a student:
The average waiting time in a queue (Wq) can be calculated using Little's Law: Wq = Lq / λ, where Lq is the average number of customers in the queue and λ is the arrival rate. In this case, λ (arrival rate) = 1 customer per 12 minutes, and Lq can be calculated using the queuing formula: Lq = ρ^2 / (1 - ρ). Plugging in the values: Lq = (5/6)^2 / (1 - 5/6) = 25/6 ≈ 4.17 customers Wq = Lq / λ = 4.17 / (1/12) = 50 minutes. Therefore, on average, a student spends approximately 50 minutes waiting in line.
(c) Average length of the line: The average number of customers in the system (L) can be calculated using Little's Law: L = λ * W, where W is the average time a customer spends in the system. In this case, λ (arrival rate) = 1 customer per 12 minutes, and W can be calculated as W = Wq + 1/μ, where μ is the service rate (1/10 customers per minute). Plugging in the values: W = 50 + 1/ (1/10) = 50 + 10 = 60 minutes. L = λ * W = (1/12) * 60 = 5 customers. Therefore, on average, the line consists of approximately 5 customers.
(d) Probability of finding at least one student waiting in line: The probability that an arriving student finds at least one other student waiting in line is equal to the probability that the system is not empty. The probability that the system is not empty (P0) can be calculated using the formula: P0 = 1 - ρ, where ρ is the utilization. Plugging in the values:
P0 = 1 - 0.8333 ≈ 0.1667. Therefore, the probability that an arriving student will find at least one other student waiting in line is approximately 0.167.
To learn more about Probability, click here: brainly.com/question/16988487
#SPJ11
1. The nature of time series data True or False: For time series data sets, the time at which each observation is made is important; however, that is not the case for cross-sectional data. True False
Answers
True. Time series data refers to a collection of observations gathered over time, where the time dimension is a critical component of the data.
Each data point is linked to a specific point in time. In contrast, cross-sectional data is collected at a single point in time and does not have a time dimension. Therefore, the timing of each observation is crucial in time series data but not as important in cross-sectional data.
Time series data is a sequence of data points indexed in time order. It is used to track change over time.
Cross-sectional data is a snapshot of data at a specific point in time. It is used to compare different groups or variables .
Think about how the time at which each observation is made affects the analysis of time series data and cross-sectional data.
to learn more about Time series data click here:
brainly.com/question/29097191
#SPJ11
38 x 97 help help help
Answers
Answer:
3686
Step-by-step explanation:
2 of 6
Brian and Colin are marking exam papers.
Each set takes Brian 43 minutes and Colin
1 hour. Express the times Brian and Colin
take as a ratio in its simplest form.
Answers
Step-by-step explanation:
Brian takes = 43 minutes
Colin takes = 1 hour = 60 minutes
In ratio,
43/60
Which of the following represents the range of the function table?
A. {-3, 1, 7}
B. {-6, -3, -2, 1, 5, 7}
C. {0, 1, 2, 3, 4, 5, 6}
D. {-6, -2, 5}

Answers
The range of the given table would be set of all possible y-values as {-6, -2, 5} which is the correct answer would be an option (D).
What are the domain and range of the function?The domain of the function includes all possible x values of a function, and the range includes all possible y values of the function.
We have been given that table as:
x y
-3 -6
1 -2
7 5
As per the given table, the required solution would be as:
The range of a function is the set of all possible output values of the function. In this case, the output values of the function are the y-values in the table. The range of the function table is the set of all possible y-values, which in this case is {-6, -2, 5}.
Therefore, the range of the function table is therefore -6 to 5.
Learn more about the domain and the range here:
brainly.com/question/21027387
#SPJ2
5x+64=-20
9 +2x=25
Solve the system of equations
Answers
The values of the variables are x = -16.8 and x = 8
What are algebraic expressions?Algebraic expressions are defined as expressions that are composed of varaibles, coefficients, terms, constants and factors.
These algebraic expressions are also made up of mathematical operations, such as;
BracketDivisionParenthesesSubtractionMultiplicationFrom the information given, we have that;
5x+64=-20
collect the like terms, we get;
5x = -20 - 64
subtract the values
5x = -84
Divide by the coefficient, we have;
x = - 16. 8
Also,
9 +2x=25
collect like terms
2x = 16
Divide by the coefficient
x = 8
Learn about algebraic expressions at: https://brainly.com/question/4344214
#SPJ1
Someone please help me out! I’m too lost pls thank you so much :( pls don’t ignore

Answers
Answer:
its abcd
this is the answer because its asking you for the pattern
hope i helped, TRUST ME ITS RIGHT
I just took a project and got a bad grade on it my teacher wrote this, It looks like you made a calculation error with the radius measurement in your work. Take a look at the comments I left on your paper. You may revise your work and resubmit and I will regrade your project. This is my work. Please help

Answers
The areas that needs correction has been attended to and they include the following:
4.)533.8 meters
5.)22686.5 m²
8.)19.06 m
How to determine the radius of a circle?To determine the radius of a circle, the diameter should be divided into two.
For the wheel, the radius is calculated as follows;
Diameter = 150/2
= 85 meters.
For 4.)
The circumference of the wheel with the given radius;
Formula = 2πr
= 2×3.14×85
= 533.8 meters
For 5.)
Area of the wheel = πr²
= 3.14×85×85 = 22686.5 m²
For 8.) The arc length between the two cars;
= circumference/number of compartment
= 533.8/28
= 19.06 m
Learn more about area here:
https://brainly.com/question/28470545
#SPJ1
what is the probability that headway is within 1 standard deviation of the mean value? (round your answer to three decimal places.)
Answers
The probability that headway is within 1 standard deviation of the mean value is 0.890.
What is mean value?
By dividing the sum of the given numbers by the entire number of numbers, the mean—the average of the given numbers—is determined.
The mean of a discrete probability distribution of a random variable X is equal to the sum over all possible values weighted by the likelihood of each value. To calculate the mean, one must multiply each potential value of X by its probability P(x), then add all of these products.
Given mean value is P( 0.995 ≤ x ≤ 1.445) = F(1.445) - F(0.995).
The cdf for the distribution is
\(F(x)=\left \{ {{1 -\frac{1}{x^6} ,x > 1} \atop {0,x\le 1}} \right.\)
Now calculate the value of F(1.445) and F(0.995).
F(1.445) = 1 - (1/(1.445)⁶)
F(0.995) = 0
Now putting the value of F(1.445) and F(0.995) in P( 0.995 ≤ x ≤ 1.445) = F(1.445) - F(0.995):
P( 0.995 ≤ x ≤ 1.445)
=1 - (1/(1.445)⁶) - 0
=0.890
To learn more about standard deviation, click on below link:
https://brainly.com/question/15059898
#SPJ4
If 0.000006493 was written in scientific notation, what would be the exponent?
Answers
Answer:
6.493×10^ -6
.............exponent= -6
consider a predicate p. suppose that we proved p(-2) and p(0). find the set of integers k for which p(k) is proved true if we also prove that p(k)^p(k 2)=> p(k-2)
Answers
The set of integers for which p(k) is true is all even integers for which p(k) is proved true if we also prove that p(k)^p(k 2)=> p(k-2).
Considering that p(- 2) and p(0) are valid and expecting that p(k)^p(k+2) => p(k-2), we can decide the arrangement of numbers k for which p(k) is valid by acceptance. In particular, we can show that p(k) is valid for all even numbers k by enlistment, as follows.
To begin with, since p(- 2) and p(0) are valid, the base instance of k = - 2 is valid.
Then, expect that p(k) is valid for some even number k. Then, at that point, utilizing the given ramifications, we have p(k+2) is valid.
At long last, utilizing a similar ramifications once more, we have that p(k-2) is valid. Accordingly, by acceptance, we have shown that p(k) is valid for all even numbers k.
To learn more about mathematical induction, refer:
https://brainly.com/question/29584620
#SPJ4
please help me with this question

Answers
Answer:
V = 3 * 3 * 7 + 2 * 3 * 5 = 63 + 30 = 93 just adding 2 segments
4. Xander pays $8 for 10 skateboard stickers. There is a proportional relationship between the number of stickers Xander buys, x, and the total cost, y. Equation:
Answers
Answer:8x=10y
Step-by-step explanation:
A proportional relationship between the number of stickers Xander buys, x, and the total cost, y is 8x=10y.
Given that, Xander pays $8 for 10 skateboard stickers.
What is a proportional relationship?Proportional relationships are relationships between two variables where their ratios are equivalent. Another way to think about them is that, in a proportional relationship, one variable is always a constant value times the other. That constant is know as the "constant of proportionality".
Given, the number of stickers Xander buys, x, and the total cost, y.
Now, 8x=10y
⇒ x/y = 10/8
Therefore, a proportional relationship between the number of stickers Xander buys, x, and the total cost, y is 8x=10y.
To learn more about the proportional relationship visit:
https://brainly.com/question/12917806.
#SPJ5
GIVING BRAINLIEST AFTER TWO ANSWERS ARE GIVEN!!! WILL CHOOSE THE BEST ONE!!! ( the answer is either yes or no )

Answers
Answer:
no
Step-by-step explanation:
she did run/rise instead of rise/run
In a two-tailed test, a statistician got a z test statistic of 1.47. What is the p-value? Select one: a. .0708 b. .1416 c. .0874 d. .0301
Answers
The p-value is 2 * 0.0708 = 0.1416.
To find the p-value associated with a z test statistic of 1.47 in a two-tailed test, we need to calculate the probability of observing a test statistic as extreme or more extreme than 1.47 in both tails of the standard normal distribution.
The p-value is the probability of observing a test statistic as extreme or more extreme than the observed value. In a two-tailed test, we need to consider both tails.
To find the p-value, we can use a standard normal distribution table or a statistical calculator. In this case, using a standard normal distribution table, we find that the area to the right of 1.47 is 0.0708.
Since it is a two-tailed test, we need to consider both tails. Therefore, the total p-value is twice the area in one tail.
Know more about probability here:
https://brainly.com/question/32004014
#SPJ11