A caterpillar crawling in a straight line across a coordinate plane starts at point (-3, -4) and ends at point (25, 38). Counting the start point and end point, how many points with integer coordinates does the caterpillar touch?
Answers
Answer:
15 points
Step-by-step explanation:
The start and end point of the caterpillar path are;
Start point = (-3, -4)
End point = (25, 38)
The slope of the caterpillar's path, 'm', given the 'x', and y-coordinates of two points is given by the following formula;
\(Slope, \, m =\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Therefore, m = (38 - (-4))/(25 - (-3)) = 1.5
The equation of the caterpillar's path in point and slope form is given as follows;
y - (-4) = 1.5 × (x - (-3))
y + 4 = 1.5 × (x + 3)
y + 4 = 1.5·x + 4.5
y = 1.5·x + 4.5 - 4 = 1.5·x + 0.5
y = 1.5·x + 0.5
Given that the 0.5 is added to the product of 'x' and 1.5, the points that have both integer points for 'x', and 'y' are the points that have odd number values of 'x', as follows;
(-3, -4), (-1, -1), (1, 2), (3, 5), (5, 8), (7, 11), (9, 14), (11, 17), (13, 20), (15, 23), (17, 26), (19, 29), (21, 32), (23, 35), (25, 38)
Therefore, we have 15 points counting the start and end points with integer coordinates
Related Questions
What is heron's formula
Answers
Answer:
\(\boxed{A=\sqrt{s(s-a)(s-b)(s-c)}}\)
Step-by-step explanation:
We can use Heron’s formula to determine the area of a triangle when three side lengths of a triangle are given.
\(s=\frac{a+b+c}{2}\)
\(s : \mathrm{semi \: perimeter}\)
\(A=\sqrt{s(s-a)(s-b)(s-c)}\)
\(A : \mathrm{area}\)
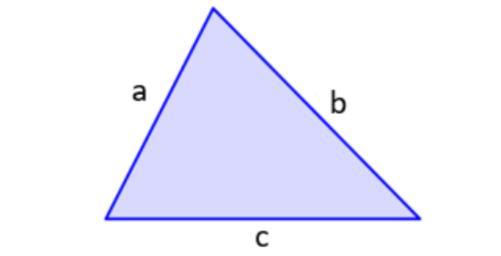
Answer:
Heron's formula gives the area of a triangle when the length of all three sides are known. Use Heron's formula to find the area of triangle ABC, if AB=3,BC=2,CA=4 . Substitute S into the formula . Round answer to nearest tenth.
Step-by-step explanation:
What is the symbol ~, if you're trying to find the probability of ~A?
the addition probability
the probability of the event not happening
the multiplication probability
None of these choices are correct.
Answers
The symbol ~ (tilde) is commonly used to represent the negation or complement of an event. When we refer to ~A, it means "not A" or "the complement of A." In terms of probability, ~A represents the event not happening or the event A occurring.
The square on the right is a scaled copy of the square on the left. Identify the scale factor. Express your answer in simplest form.

Answers
In a roll of 50 pennies, there are 12 dated 1977. If a penny is drawn at random, what is the probability that it is dated 1977?
Answers
The probability of drawing a penny dated 1977 is 0.24 or 24%.
What is Probability:Probability is a branch of mathematics that deals with the study of random events. It is used to measure the likelihood or chance of a particular event occurring.
Probability is expressed as a fraction or a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain.
The probability of drawing a penny dated 1977 can be found by dividing the number of pennies dated 1977 by the total number of pennies.
Here we have
Total number of pennies = 50
Number of pennies dated 1977 = 12
Probability of drawing a penny dated 1977
= Number of pennies dated 1977 / Total number of pennies
= 12 / 50
= 0.24
Therefore,
The probability of drawing a penny dated 1977 is 0.24 or 24%.
Learn more about Probability at
https://brainly.com/question/29221515
#SPJ1
Eric and Erica collect phone cards, and their phone
cards are in a ratio of 3:4. If Erica has 14 more phone
cards than Eric, how many cards does Eric have?
Answers
Answer:
18.67
Step-by-step explanation:
my calculate ratio results
How much will a person pay for 13.5 pounds of bananas at a price of $1.68
Answers
Answer:$15.18
Step-by-step explanation:
using the data on this scatter plot

Answers
Answer:
\( - 8(45) + 482 = - 360 + 482 = 122\)
What change do you have to make to the graph of f (x) = 7x in order to graph the function g (x) = 7x+10?
Answers
To graph the function g(x) = 7x + 10, we shift the graph of f(x) = 7x vertically by adding a constant term of +10. This means every y-coordinate on the graph increases by 10 units. The slope of the line remains the same at 7. The resulting graph is a straight line passing through (0, 10) with a slope of 7.
To graph the function g(x) = 7x + 10, you need to make the following change to the graph of f(x) = 7x:
1. Translation: The graph of f(x) = 7x can be shifted vertically by adding a constant term to the equation. In this case, the constant term is +10.
Here's how you can do it step by step:
1. Start with the graph of f(x) = 7x, which is a straight line passing through the origin (0,0) with a slope of 7.
2. To shift the graph vertically, add the constant term +10 to the equation. Now, the equation becomes g(x) = 7x + 10.
3. The constant term of +10 means that every y-coordinate of the points on the graph will increase by 10 units. For example, the point (0,0) on the original graph will shift to (0,10) on the new graph.
4. Similarly, if you take any other point on the original graph, such as (1,7), the corresponding point on the new graph will be (1,17) since you add 10 to the y-coordinate.
5. Keep in mind that the slope of the line remains the same, as only the y-values are affected. So, the new graph will still have a slope of 7.
By making this change, you will have successfully graphed the function g(x) = 7x + 10.
For more such questions graph,Click on
https://brainly.com/question/19040584
#SPJ8
Which negative angle is equivalent to an 85° angle?
A. An angle measuring -95°
B. An angle measuring -275°
C. An angle measuring -85°
D. An angle measuring -265°
Answers
Which negative angle is equivalent to an 85° angle?
A. An angle measuring -95°
B. An angle measuring -275°
C. An angle measuring -85°D. An angle measuring -265°
-KeonLee
I hope it help
#Carry on learning
An angle measuring -275°
*view photo*

classify the following differential equation s given in both standard and differential form. Q5 only

Answers
y' = 2xy + x
Rewriting it in differential form, we get:
(2xy + x)dx - dy = 0
This is a first-order linear differential equation, which can be written in the form:
y' + P(x)y = Q(x)
where P(x) = -2x and Q(x) = x.
Therefore, the differential equation is a first-order linear differential equation.
what is the value of x^2 - 6x + 9 when x = 2 + i?
Answers
The Expression x^2 - 6x + 9 when x = 2 + i is -2i
To evaluate the expression x^2 - 6x + 9 when x = 2 + i, we substitute the value of x into the expression:
(2 + i)^2 - 6(2 + i) + 9
Simplifying the first term, we get:
(2 + i)^2 = 2^2 + 2(2)(i) + i^2 = 4 + 4i + i^2
Since i^2 = -1, we can substitute that in and simplify further:
(2 + i)^2 = 4 + 4i - 1 = 3 + 4i
Now we substitute this into the original expression:
(2 + i)^2 - 6(2 + i) + 9 = (3 + 4i) - 6(2 + i) + 9
Simplifying further, we get:
= 3 + 4i - 12 - 6i + 9
= 0 - 2i
= -2i
Therefore, the value of x^2 - 6x + 9 when x = 2 + i is -2i.
To know more about Expression .
https://brainly.com/question/1859113
#SPJ11
A waiter earned a 25% tip. What decimal is equivalent to 25%?
Answers
how many solutions does the eqaution below have? 4x-3-2x+5=6-3x+2+5x
Answers
Answer:
4x - 3 - 2x + 5 = 6 - 3x + 2 + 5x
2x + 2 = 2x + 8
2 ≠ 8, so this equation has no solutions.
Answer:
No solution
Step-by-step explanation:
Given:
\(4x-3-2x+5=6-3x+2+5x\)
rearrange terms so like terms are together
\(4x-2x-3+5=6+2-3x+5x\)
combine like terms
\(2x+2=8+2x\)
subtract 2x to both sides
\(2\neq 8\)
2 doesn't equal 8, meaning that there are 0 solutions to this problem.
Hope this helps! :)
Solve ARST.
R
S
72°
7
T
15
r
S

Answers
Answer:
r = 14.3s = 4.6S = 18°Step-by-step explanation:
You want the solution to right triangle RST with RS = 15, R = 72°, T = 90°.
Trig relationsThe mnemonic SOH CAH TOA reminds you ...
Sin = Opposite/Hypotenuse ⇒ r = 15·sin(72°) ≈ 14.3
Cos = Adjacent/Hypotenuse ⇒ s = 15·cos(72°) ≈ 4.6
The acute angles in a right triangle are complementary, so ...
S = 90° -R = 90° -72° = 18°

Mid topic checkpoint chapter 4 for questions 3,and 4

Answers
3) The equation of the linear model would be y = 7.5x+60.
4) If Adam studies for 6 hours then his score would be 88.
What is the Linear equation?
An algebraic equation with only a constant and a first-order (linear) term is said to be linear if it has the formula y = mx + b, where m is the slope and b is the y-intercept. The above is occasionally referred to as a "linear equation with two variables," where y and x are the variables.
y = mx + c
where m denotes the slope.
The y-intercept is represented by the constant c. (Where x is zero)
In our instance, y-intercept equals 60.
The line's equation will therefore be:
y = mx + 60
y = mx + 60
There are given the line's coordinates (4, 90). These considerations will thus satisfy the equation.
90 = 4*m + 60
4.m = 30 m = 7.5 m = 7.5 y = 7.5x + 60 y = 7.5 * 6 + 60 y = 45 + 60 y = 105 is
y = 7.5x + 60.
If Adam's study for 6 hours then his score would be
y = 7.5x + 60.
y = 7.5(6) + 60
y = 105
Hence,
3) The equation of the linear model would be y = 7.5x+60.
4) If Adam studies for 6 hours then his score would be 88.
To learn more about equations refer to:
brainly.com/question/4344214
#SPJ1
Heather invests $1,050 in an account with a 3.5% interest rate, making no other deposits or withdrawals. What will Heather’s account balance be after 7 years if the interest is compounded 6 times each year?
Answers
Heather's account balance will be approximately $1,340.55 after 7 years if the interest is compounded 6 times each year.
What is the accrued amount after 7 years?To solve this problem, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A is the account balance after a certain amount of time
P is the principal or initial amount invested
r is the annual interest rate (as a decimal)
n is the number of times the interest is compounded per year
t is the time period in years
Given tha data in the question;
P = $1,050R = 3.5%n (the interest is compounded 6 times each year) = 6t = 7 yearsFirst, convert R as a percent to r as a decimal
r = R/100
r = 3.5/100
r = 0.035 rate per year.
Substituting these values into the formula solve for accrued amount, we get:
A = P(1 + r/n)^(nt)
A = 1,050(1 + 0.035/6)^(6 × 7)
A = 1,050(1 + 0.005833333333333)⁴²
A = 1,050(1.005833333333333333)⁴²
A = $1,340.55
Therefore, the accrued amount is $1,340.55.
Learn more about compound interest here: brainly.com/question/27128740
#SPJ1
How much would $200 invested at 5% interest compounded monthly be
worth after 9 years?
Answers
9514 1404 393
Answer:
$313.37
Step-by-step explanation:
The compound interest formula is used to find that value.
A = P(1 +r/12)^(12t)
P compounded monthly at annual rate r for t years.
A = $200(1 +0.05/12)^(12·9) ≈ $313.37
What?
AAeEeEeEeOOoooO
h??
Eeb
Answers
Hello!
What am i doing with my life?
In a certain chemical, the ratio of zinc to copper is 3 to 19. A jar of the chemical contains 874 grams of copper. How many grams of zinc does it contain?
It contains
grams of Zinc
Answers
Answer:
138 grams of zinc
Step-by-step explanation:
Zinc : copper = 3 : 19
Let amount of zinc = 138 grams
3 : 19 :: x : 874
Product of means = product of extremes
19 * x = 3 * 874
x = \(\frac{3*874}{19}\)
x = 3 * 46
Zinc = 138 grams
\(\underline{\underline{\sf \bigstar \qquad Solution \qquad \: \bigstar}} \\ \)
Copper and Zinc in the ratio = 3:19Weight of copper in chemical = 874 gramsLet weight of copper be 3x and weight of zinc be 19x.
☯ \(\underline{\boldsymbol{According\: to \:the\: Question\:now :}} \\\)
\(:\implies \textsf {Total weight = weight of copper + weight of zinc} \\ \\ \\ \)
\(:\implies \textsf {Total weight = 3x +19x} \\ \\ \\ \)
\(:\implies \underline{ \boxed{ \textsf {Total weight = 22x}}} \\ \\ \\ \)
⠀⠀━━━━━━━━━━━━━━━━━━━━━━━━
\(\dashrightarrow\:\:\textsf{ Weight of chemical = weight of zinc + weight of copper} \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 22x = 3x + 19x \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 22x = 3x + 874 \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 22x - 3x = 874 \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 19x = 874 \\ \\ \\ \)
\(\dashrightarrow \: \: \sf x = \dfrac{874}{19} \\ \\ \\ \)
\(\dashrightarrow \: \: \underline{\boxed{ \sf x = 46}} \\ \\ \\\)
⠀⠀━━━━━━━━━━━━━━━━━━━━━━━━━━━
\(\bigstar\:\underline{\frak{Finding \: the \: weight \: of \: the \: zinc \: in \: a \: chemical : }}\)
\(\longrightarrow\:\:\sf weight \: of \: zinc = 3x \\ \\ \\ \)
\(\longrightarrow\:\:\sf weight \: of \: zinc = 3 \times 46 \\ \\ \\ \)
\(\longrightarrow\:\: \underline{ \boxed{\sf weight \: of \: zinc =138 \: grams}} \\ \\ \\ \)
\(\therefore\:\underline{\textsf{The chemical contains \textbf{138 grams}} \textsf{ of zinc}}. \\ \)
In your own words, tell me the difference between a geometric and an arithmetic sequence.
Answers
As several differences are there between them and is differentiated below.
What is Sequence?
A list of numbers in a specific order is called a sequence. The terms of the sequence are the various numbers that appear in it.
Let a sequence's terms be a1, a2, a3,..., an,..., etc.
The term's position is indicated by the subscripts. That implies,
Initial phrase = a1
term two = a2
term three Equals a3
….
The nth term, indicated by an, is the number that appears in the sequence at the nth place. This phrase is also known as the sequence's general phrase.
Geometric Sequence:
It is a sequence of numbers in which each new term is calculated by multiplying by a non-zero and fixed number.Multiplication or Division is done in every step.A common ratio between 2 successive terms is the common ratio.It is of the Exponential Form.Arithmetic Sequence:
It is a list of numbers, in which every new term alters from another preceding term by a definite quantity.Addition or Subtraction is done in every step.A common ratio between 2 successive terms.It is of the Linear Form,To learn more about Sequence, visit:
https://brainly.com/question/21961097
#SPJ1
Please Help - Find the Volume
I know the answer is 1982.0 ft³. However, I don't know how to get to that answer. I keep getting 2112ft³.

Answers
Answer:
1982.0 ft³
Step-by-step explanation:
The composite figure can be decomposed into a cube and a square pyramid. The volume is the sum of the volumes of these.
__
pyramidThe square base of the pyramid is 12 ft on each side, so the diagonal of the base is 12√2 feet. (The diagonal of a square is √2 times the side length.) Then the distance from a corner to the center of the base is half that, or 6√2 feet.
That distance and the height of the pyramid form a right triangle whose hypotenuse is the given 10 ft measure of the length of the edge of a face of the pyramid. Then the height can be found using the Pythagorean theorem:
h² +(6√2)² = 10²
h² = 100 -72 = 28
h = 2√7 ≈ 5.291503 . . . ft
The volume of the pyramid is ...
V = 1/3Bh = 1/3s²h
V = 1/3(12 ft)²(5.2910503 ft) ≈ 253.992 ft³
__
cubeThe volume of a cube is given by ...
V = s³
V = (12 ft)³ = 1728 ft³
__
total volumeThe total volume of the figure is the sum of the pyramid volume and the cube volume:
total volume = 253.992 ft³ +1728 ft³ = 1981.992 ft³
The volume of the figure is about 1982.0 ft³.
_____
Additional comment
Your figure for the volume seems to assume the height of the pyramid is 8 feet. That length is the slant height of one face of the pyramid. It would be the hypotenuse of a right triangle whose other legs are 6 ft and the height of the pyramid. Then we would have ...
h² +6² = 8²
h² = 64 -36 = 28 . . . . as above
The pyramid height is the perpendicular distance from the plane of the base to the peak. It is measured through the middle of the volume, not along one face.
Abe can mow a lawn in 3 hours. After he has been working for 1/3 hour, Bob helps, and working together, it takes 1 and 2/3 hours more to finish the job. How long would it take Bob to mow the lawn by himself?
Please show work.
Answers
Bob would take 5 hours to mow the law by himself.
Let us consider, the area of the lawn to be mowed to be x inch².
It is given that the law can be mowed by Abe alone in 3 hours.
We know that,
Rate of work = Work/Time
⇒ rate of work of Abe = area to be mowed(work)/time taken
= (x/3) inch²/hour
Now,
Abe has been working alone for 1/3 hour
⇒work done by Abe alone = rate of work of Abe x time
= (x/3) inch²/hour x 1/3 hour
= x/9 inch²
Remaining work = x - x/9 = 8x/9 inch²
Let, the rate of work of Bob be y inch²/hour.
It is given that the time taken by Abe and Bob to complete the remaining work together is 1 and 2/3 hours, i.e, 5/3 hours.
Therefore,
The rate of work of Abe and Bob when working together
= work ÷ time
=(8x/9) ÷ (5/3)
=8x/15 inch²/hour
⇒ Rate of work of Abe + Rate of work of Bob = 8x/15
⇒ x/3 + y = 8x/15
⇒ y = (8x/15) - (x/3)
⇒ y = 3x/15 = x/5 inch²/hour
Thus, the time taken by Bob to mow the law by himself
= work ÷ rate of work
= x inch² ÷ (x/5) inch²/hour
= 5 hours
So, it would take 5 hours for Bob to mow the lawn alone.
To know more about Time and Work,
https://brainly.com/question/13086625
A study was conducted showing the relationship between the average maintenance cost and the age of a car in years.
Number of observations: 13
Least Squares | Standard | T
Parameter | Estimate | Error | Statistic| P-Value
Intercept | 54.7757 | 54.87 | 0.998282 | 0.3396
Slope | 120.689 | 11.8442 | 10.1898 | 0.0000
a) What is the formula for the regression function based on the output above (Write your equation in the context of question)?
b) Interpret the slope of the regression equation (In the context of question)?
c) Construct an 95% interval to predict the maintenance cost for a car that is 7 years old?
d) Based on this analysis, can we conclude that a relationship exists between the maintenance cost and the age of the car in years? What is the null and alternative hypothesis? Justify your answer using three steps process.
Answers
Answer:
Step-by-step explanation:
a) The formula for the regression function is:
Maintenance Cost = 54.7757 + 120.689 x Age of Car
b) The slope of the regression equation is 120.689. This means that on average, for every one year increase in the age of a car, the maintenance cost is expected to increase by $120.689.
c) To construct a 95% interval to predict the maintenance cost for a car that is 7 years old, we can use the formula:
Y = a + bX ± tα/2 * SE
where Y is the predicted maintenance cost, a is the intercept, b is the slope, X is the age of the car, tα/2 is the t-value for the 95% confidence level with n-2 degrees of freedom (11 in this case), and SE is the standard error of the estimate.
Plugging in the values, we get:
Y = 54.7757 + 120.689 * 7 ± 2.201 * 11.8442
Y = 923.167 ± 26.010
Therefore, we can be 95% confident that the maintenance cost for a car that is 7 years old will be between $897.16 and $949.17.
d) The null hypothesis is that there is no significant linear relationship between the average maintenance cost and the age of a car in years. The alternative hypothesis is that there is a significant linear relationship between the average maintenance cost and the age of a car in years.
To test the hypothesis, we can perform a t-test on the slope coefficient using the t-statistic and the p-value provided in the output. The t-statistic is 10.1898, which is much greater than the critical t-value at the 0.05 level of significance for a two-tailed test with 11 degrees of freedom (2.201). The p-value is 0.0000, which is less than the significance level of 0.05. Therefore, we can reject the null hypothesis and conclude that there is a significant linear relationship between the maintenance cost and the age of the car in years.
AT&T would like to test the hypothesis that the proportion of 18- to 34-year-old Americans that own a cell phone is less than the proportion of 35- to 49-year-old Americans. A random sample of 200 18- to 34-year-old Americans found that 126 owned a smartphone. A random sample of 175 35- to 49-year-old Americans found that 119 owned a smartphone. If Population 1 is defined as 18- to 34-year-old Americans and Population 2 is defined as 35- to 49-year-old Americans, the correct hypothesis statement for this hypothesis test would be
Answers
Answer:
The null and alternative hypothesis can be written as:
\(H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2< 0\)
Step-by-step explanation:
This is a hypothesis test for the difference between proportions.
The claim is that the proportion of 18- to 34-year-old Americans that own a cell phone is less than the proportion of 35- to 49-year-old Americans.
This claim will be reflected in the alternnative hypothesis, that will state that the population proportion 1 (18 to 34) is significantly smaller than the population proportion 2 (35 to 49).
On the contrary, the null hypothesis will state that the population proportion 1 is ot significantly smaller than the population proportion 2.
Then, the null and alternative hypothesis can be written as:
\(H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2< 0\)
The significance level is assumed to be 0.05.
The sample 1, of size n1=200 has a proportion of p1=0.63.
\(p_1=X_1/n_1=126/200=0.63\)
The sample 2, of size n2=175 has a proportion of p2=0.68.
\(p_2=X_2/n_2=119/175=0.68\)
The difference between proportions is (p1-p2)=-0.05.
\(p_d=p_1-p_2=0.63-0.68=-0.05\)
The pooled proportion, needed to calculate the standard error, is:
\(p=\dfrac{X_1+X_2}{n_1+n_2}=\dfrac{126+119}{200+175}=\dfrac{245}{375}=0.653\)
The estimated standard error of the difference between means is computed using the formula:
\(s_{p1-p2}=\sqrt{\dfrac{p(1-p)}{n_1}+\dfrac{p(1-p)}{n_2}}=\sqrt{\dfrac{0.653*0.347}{200}+\dfrac{0.653*0.347}{175}}\\\\\\s_{p1-p2}=\sqrt{0.001132+0.001294}=\sqrt{0.002427}=0.049\)
Then, we can calculate the z-statistic as:
\(z=\dfrac{p_d-(\pi_1-\pi_2)}{s_{p1-p2}}=\dfrac{-0.05-0}{0.049}=\dfrac{-0.05}{0.049}=-1.01\)
This test is a left-tailed test, so the P-value for this test is calculated as (using a z-table):
\(\text{P-value}=P(z<-1.01)=0.1554\)
As the P-value (0.1554) is bigger than the significance level (0.05), the effect is not significant.
The null hypothesis failed to be rejected.
There is not enough evidence to support the claim that the proportion of 18- to 34-year-old Americans that own a cell phone is less than the proportion of 35- to 49-year-old Americans.
Henry's family drove 425 miles. How many more
miles do they need to drive to reach 1,000 miles?
Answers
Answer:
I'm pretty sure the answer is 575 :D
Step-by-step explanation:
1,000 minus 425 is 575. have a good day!
Class: Algebra 2
I need help with these Natural Logarithms problems!!!!!
I will give lots of points!!!!

Answers
The solutions are: x = ln(2) for 2eˣ = 4, x = ln(25)/4 for e⁴ˣ = 25, x = ln(72) for eˣ = 72 and x = ln(124)/3 for e³ˣ = 124.
Solving equations using natural logarithmTo solve these equations using natural logarithm, we can use the following rules:
If a = eᵇ, then b = ln(a).If ln(aᵇ) = b ln(a).Using these rules, we can solve the given equations as follows:
2eˣ = 4
Divide both sides by 2 to get
eˣ = 2.
Take the natural logarithm of both sides to get
ln(eˣ) = ln(2).
Using rule 1 above, we can simplify ln(eˣ) to x, and we get
x = ln(2).
e⁴ˣ = 25
4x = ln(25).
Divide both sides by 4 to get
x = ln(25)/4.
eˣ = 72
Take the natural logarithm of both sides to get
x = ln(72).
e³ˣ = 124
Take the natural logarithm of both sides to get
3x = ln(124).
Divide both sides by 3 to get
x = ln(124)/3.
For the second set of equations, we use the same rule as above
So, we have
ln(x - 3) = 2
x - 3 = e²
x = e² + 3.
x ≈ 10.389.
Therefore, the solution is x ≈ 10.389.
ln(2t) = 4
2t = e⁴
t = 0.5 * e⁴
t ≈ 27.299.
Therefore, the solution is t ≈ 27.299.
Read more about logarithm at
https://brainly.com/question/24160402
#SPJ1
pls help
show work pls

Answers
Answer:
1. x=17
y= 7 1/3
2. x= 6 2/3
y=1.7
Step-by-step explanation:
4x=68 because it is isosceles triangle
x=17
y+1/2= 7 5/6
y= 7 1/3
can you maybe just give me the answer please because I'm running out of time to turn this in. thank you so much

Answers
A linear function must satisfy the condition that the slope between any two points must remain the same.
Use this fact to find pairs of points which do not satisfy that condition. That will tell you which options are not linear functions.
A)
The slope of points (-2,0) and (1,-3) is -1 while the slope of points (1,-3) to (3,-6) is -3/2. Then, this is not a linear function.
B)
The slope of every pair of numbers here is 2. Then, this set represents a linear function.
C)
The slope of points (-7,-7) and (-3,-4) is 3/4 while the slope of points (-3,-4) and (0,-1) is -1. Then, this is not a linear function.
D)
The slope of points (3,3) and (5,4) is 1/2 while the slope of (5,4) and (7,6) is 1. Then, this is not a linear function.
Therefore, the answer is:
\(B\)Calculer la moyenne de la série suivante :
Valeurs 7 8 9 10 11 12 13 14 15 16 18
Effectifs 7 1 1 1 1 3 2 1 1 1 1
On donnera la réponse sous la forme d'un entier relatif ou d'un nombre décimal.
Answers
Answer:
Pour calculer la moyenne, nous devons multiplier chaque valeur par sa fréquence, additionner tous les produits, puis diviser par la fréquence totale.
Le calcul ressemblerait à ceci :
(7 * 7) + (8 * 1) + (9 * 1) + (10 * 1) + (11 * 1) + (12 * 3) + (13 * 2) + (14 * 1) + (15 * 1) + (16 * 1) + (18 * 1)
= 49 + 8 + 9 + 10 + 11 + 36 + 26 + 14 + 15 + 16 + 18
= 238
Fréquence totale = 7 + 1 + 1 + 1 + 1 + 3 + 2 + 1 + 1 + 1 + 1 = 21
Moyenne = 238/21 = 11,333
La moyenne de la série est de 11,3333.
The transformation rule (x, y) - (1.5x, 1.5y) (x, y) – (1.5x,1.5y) wouldan enlargementA translationA rotationA reduction
Answers
When performing a transformation to a point on the coordinate system, if the coordinates are multiplied by a constant k the resulting transformation will be a dilation.
If k > 1 → the resulting dilation is an enlargment
If k < 1 →the resulting dilation is a reduction
For the given rule
(1.5x,1.5y)
The constant is k=1.5, the resulting transformation is an enlargement.