a bucket holds c liters of water but a jar holds d liters more how much water do they hold together
Answers
The bucket and the jar together will hold (c + d) litres of water.
What is defined as linear equation on two variables?A linear function does have a positive relationship, so increasing one variable (input variable) causes a rise in the second variable (output variable), implying that the variables have always been directly proportional. As a result, the graph of such a linear function is a straight line with a constant slope.Correspondingly, a linear equation is a first-order algebraic equation with two variables and terms with exponents of one.A linear equation in 2 variables [x and y] is any equation with the form:
ax + by = c and at least one of a or b being non-zero.
This is known as the equation's General Form.
For the given question;
The water hold by bucket = c litres.
The water hold by jar = d litres.
Thus, the water hold by both bucket and jar is is linear equation with two variable c and d.
Total water = c + d
By, varying any value the total amount of the water will also get change.
Thus, total water hold by jar and bucket is (c + d) litres.
To know more about the linear equation on two variables, here
https://brainly.com/question/24085666
#SPJ9
Related Questions
Cariyah placed $2000 into a savings account with 3.5% interest, compounded annually. Write Cariyah's total savings S(t) as a function of time in years, t.
S(t) =
Answers
Answer:
450
Step-by-step explanation:
Determine the location of the vertex and determine the nature of the vertex for the graphs of: y = x^3 - 6x^2 -15x + 7
Answers
Answer:
(5, -93) local minima, (-1, 15) local maxima
Step-by-step explanation:
differentiate this equation, we get
y' = 3x^2 - 12 x -15
the x-axis of the vertices are:
3x^2 - 12x - 15 = 0
(x-5)(3x+3) = 0
x1 = 5 and x2=-1
so the positions of the vertices are (5, -93) and (-1 , 15)
(5, -93) is the local minima, and (-1, 15) is the local maxima
What is the cost of a pair of shoes if they retail for $18.50, have a tax of 6%, and you have a coupon for 20% off after taxes
Answers
Answer:
$15.69
Step-by-step explanation:
multiply the retail price by 1.06 to get the price after taxes.
find the discounted price by multiplying the price after taxes(19.61) by 0.8 since it is 20% off to get the answer
The initial size of a culture of bacteria 1100. After 1 hour, the bacteria count is 9500.
Find the function n(t)=no
that models the population after
hours.
Find the population after 1.5 hours.
Then Find the number of hours when the number of bacteria will reach 20,000.
Sketch the graph of the population function.
Answers
To find the function n(t) that models the population of bacteria after t hours, we can use the exponential growth formula:
n(t) = n0 * e^(kt)
Where:
n(t) is the population after t hours,
n0 is the initial population size,
e is the base of the natural logarithm (approximately 2.71828),
k is the growth rate constant.
We can determine the value of k using the given information. After 1 hour, the bacteria count is 9500, which is the population at time t = 1. Plugging these values into the equation:
\(9500 = 1100 * e^(k*1)\)
To find k, we can divide both sides by 1100:
9500/1100 = e^k
Now, we can solve for k by taking the natural logarithm (ln) of both sides:
ln(9500/1100) = ln(e^k)
ln(9500/1100) = k
Now we have the value of k. We can plug it back into the exponential growth formula to obtain the function n(t):
\(n(t) = 1100 * e^(ln(9500/1100) * t)\)
To find the population after 1.5 hours, we can substitute t = 1.5 into the equation:
\(n(1.5) = 1100 * e^(ln(9500/1100) * 1.5)\)
To find the number of hours when the number of bacteria will reach 20,000, we can set n(t) equal to 20,000 and solve for t:
\(20,000 = 1100 * e^(ln(9500/1100) * t)\)
Finally, to sketch the graph of the population function, plot the values of t on the x-axis and the corresponding values of n(t) on the y-axis using the equation n(t) = 1100 * e^(ln(9500/1100) * t). The resulting graph will show the exponential growth of the bacteria population over time.
For more such questions on exponential
https://brainly.com/question/30166689
#SPJ8
You are playing in the NBA Playoffs and attempt a 3-point shot as the buzzer sounds for the end of the
game, if you make the shot your team wins! Your basketball is is traveling on a path described by the
following function: b(x) = -x2 +1.36x + 2. The net is on a level described by the following function:
n(x) = 3 between (8 < x < 8.5). Will you make the shot and win the playoffs?
You may work alone or in a group of up to 3 students total.
BONUS: How high in the air will the basketball be at its highest point?
UNITS: x is in meters, y is in meters

Answers
Since we do not know the value of u, we cannot find the time taken by the basketball to travel a distance of 8.5 meters. We cannot find the height of the basketball at its highest point.
Given that n(x) = 3 for 8 < x < 8.5.It is impossible to determine whether the shot will be made or not based solely on this information. Winning the playoffs depends on various factors, such as the score, time remaining, and the overall performance of the team.
Therefore, additional information is required to determine the outcome of the playoffs.However, to find the height of the basketball at its highest point, we need to know the equation of the trajectory of the basketball.
Assuming that the basketball follows a parabolic path, we can use the formula:
y = ax² + bx + c,
where y is the height of the basketball, and x is the horizontal distance traveled by the basketball.
To find the values of a, b, and c, we need to know three points on the trajectory of the basketball. Let's assume that the basketball is thrown from a height of 1.5 meters and lands on the floor after traveling a horizontal distance of 8.5 meters.
Therefore, the points on the trajectory of the basketball are:
(0, 1.5), (8.5/2, h), and (8.5, 0),
where h is the height of the basketball at its highest point.Substituting these values in the equation of the trajectory,
we get:
1.5 = a(0)² + b(0) + c...(1)0 = a(8.5)² + b(8.5) + c...(2)h = a(8.5/2)² + b(8.5/2) + c...(3)
Simplifying equations (1) and (2),
we get:
c = 1.5...(4)b = -a(8.5)²/8.5...(5)
Substituting equation (4) in equation (3), we get:
h = a(8.5/2)² + b(8.5/2) + 1.5h = a(8.5/2)² - a(8.5)²/8.5 + 1.5h = -29.375a + 1.5
Substituting the value of a from equation (5) in the above equation,
we get:
h = -29.375(-a(8.5)²/8.5) + 1.5h = 0.5a(8.5)² + 1.5
Therefore, to find the height of the basketball at its highest point, we need to find the value of a. Since we know that the basketball lands on the floor after traveling a horizontal distance of 8.5 meters,
we can use the formula:
x = ut + 0.5at²,
where u is the initial horizontal velocity of the basketball, and t is the time taken by the basketball to travel a distance of 8.5 meters.
To learn more about : time
https://brainly.com/question/26862717
#SPJ8
Vehicles generally decrease in value around 14% per year. If you buy a vehicle priced at $39,500 , this can be modeled by the equation A=39500(0.86)t . Estimate the value of the vehicle after 4 years. Round to the nearest cent and do not round until the final calculation.
Answers
Rounding to the nearest cent, the estimated value of the vehicle after 4 years is approximately $23,726.20..
To estimate the value of the vehicle after 4 years, we can use the given equation A = 39500(0.86)^t, where A represents the value of the vehicle and t represents the number of years.
Substituting t = 4 into the equation:
A = 39500(0.86)^4
A ≈ 39500(0.5996)
A ≈ 23726.20
Rounding to the nearest cent, the estimated value of the vehicle after 4 years is approximately $23,726.20.
This estimation is based on the assumption that the vehicle's value decreases by 14% each year. The equation A = 39500(0.86)^t models the exponential decay of the vehicle's value over time. By raising the decay factor of 0.86 to the power of 4, we account for the 4-year period. The final result suggests that the value of the vehicle would be around $23,726.20 after 4 years of ownership.
For more such questions on estimated value
https://brainly.com/question/27898355
#SPJ8
Public school per student expenditures increased approximately linear from $1.3 Thousand in 1975 to $10.7 Thousand and 2011 predict the per student expenditure In 2024
Answers
Expenditures increase by $2200/9 per year.
Expenditure in 2024 = expenditure in 2011 + 13 years of increases
= 10100 + 13*(2200/9)
= $13,277.78
The per-student expenditure in 2024 is $14094.43.
What is slope?A line's steepness and direction are measured by the line's slope.
As per the given data:
We are given the linear variation of student expenditures.
Expenditure in 1975 = $1300
Expenditure in 2011 = $10700
The expenditure is on the y-axis and the year is on the x-axis.
The increase in expenditure per year will be given by the slope of this graph.
slope = (10700 - 1300) / (2011 - 1975)
slope = 9400/36
slope = 261.11
increase in expenditure per year = $261.11
Expenditure in 2024
= Expenditure in 2011 + increase in expenditure per year × (24 - 11)
= 10700 + 261.11 × 13
= 10700 + 3394.43
= 14094.43
The per-student expenditure in 2024 is $14094.43.
Hence, The per-student expenditure in 2024 is $14094.43
To learn more about slope, click:
brainly.com/question/3605446
#SPJ2
Ana estimated the mass of an object to be 54 grams. The actual mass of the object was 45 grams. What was the percent error in Ana’s estimate.
Answers
Answer:
20%
Step-by-step explanation:
percent error = (estimated value - real value)/(real value) × 100%
percent error = (54 - 45)/(45) × 100%
percent error = 0.2 × 100%
percent error = 20%
what is x y and z value

Answers
5x = 72
x = 72/5
x = 14.4
18/y = 9/5
90 = 9y
9y = 90
y = 90/9
y = 10
34/z = 9/5
170 = 9z
9z = 170
z = 170/9
z = 18.8° (nearest tenth)
Suppose that $9000 is placed in an account that pays 9% interest compounded each yea
Assume that no withdrawals are made from the account

Answers
Answer:
1). $9810
2). $10,620
Step-by-step explanation:
9000 x .09= 810
9000 + 810= 9810
810 x 2= 1620
9000 + 1620= 10,620
Answer: A : 810 B : 1620
Step-by-step explanation: 9000 x 9% x 1
9000 x 9% x 2
P x R x T
Principle (Money started with) x Rate ( Interest Rate) x Time (Years)
Andrea works at two different jobs. She works no more
than 40 hours per week combined between the two jobs.
At one job, she makes $12 per hour. At her other job, she
makes $16 per hour. Each week she earns at least $460.
Andrea writes a system of inequalities to represent this
situation. One of her inequalities is shown below.
x+y≤40
What should be the other inequality in Andrea's system
of inequalities?
Answers
Answer:
Second inequality is
12x + 16y ≥ 460
We also have implied inequalities x ≥ 0, y ≥ 0 meaning hours cannot be negative
Step-by-step explanation:
The other equality refers to the earnings
Let x be the hours worked in the first job
Earnings at $12 per hour = 12x
Let y be the hours worked in the second job
Earnings at $16 per hour = 16y
Total earnings = 12x + 16y
This must be at least $460
"at least" means ≥
So second inequality is
12x + 16y ≥ 460
Please help me !!! I need help asap

Answers
After calculating The perimeter of rectangle is 46.52 in the given rectangle.
What is area of rectangle?
area of rectangle can be defined as the product of length and breadth.
Given ,
A rectangle has a length 20 5 /6 and
breadth = 2 3/7
The perimeter of rectangle = 2 (l+b)
length = (120 + 5 ) / 6 = 125/ 6
breadth = (14+3) / 7 = 17/7
perimeter = 2 (125/6 + 17/7 )
= 2 ( (125*7 + 17 * 6) / 42 )
= 2 (875+102) / 42
= 2 * 23.26
= 46.52
Hence, after calculating The perimeter of rectangle is 46.52 in the given rectangle.
To learn more about area of rectangle from the given link.
https://brainly.com/question/20693059
#SPJ1
I need help please anyone ?????!!!
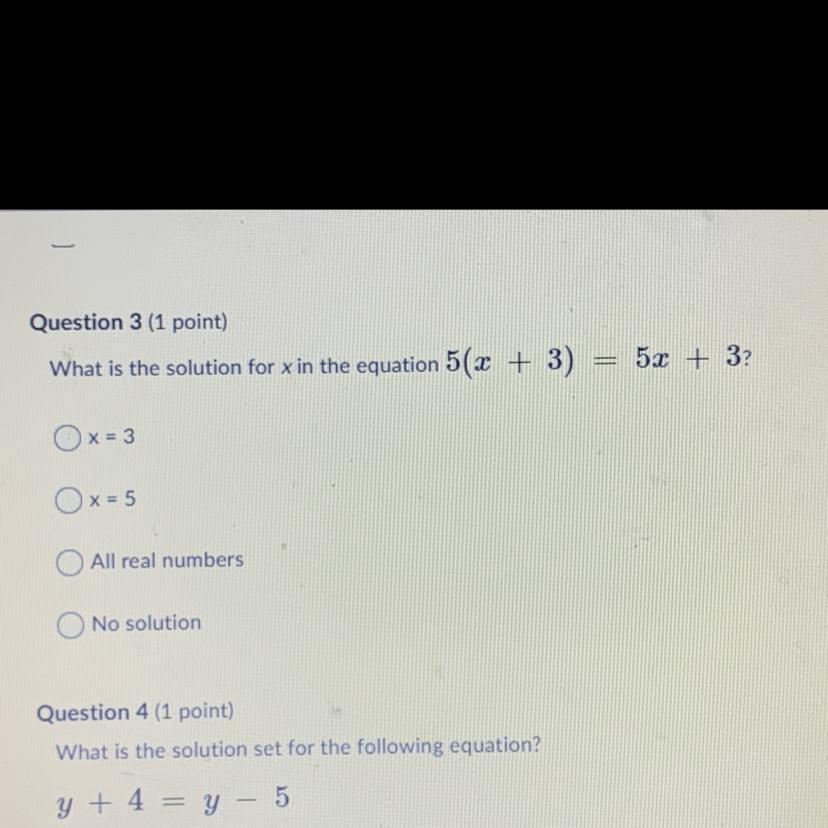
Answers
Answer:
3) No solution
4) No solution
Step-by-step explanation:
3) The equation simplifies to ...
5x +15 = 5x +3
15 = 3 . . . . . . . . . . subtract 5x; no value of x will make this true
There is no solution.
__
4) The equation simplifies to ...
4 = -5 . . . . . . . . . subtract y; no value of y will make this true
There is no solution.
Answer:
Step-by-step explanation:
What do you add to 17/4 to make 5?
Answers
The number that can be added to 17/4 to make 5 is 3/4
How to add fractionsGiven
Add to 17/4 to make 5
let
x = number addedx + 17/4 = 5
x = 5 - 17/4
x = (20-17) / 4
x = 3/4
Learn more about fraction:
https://brainly.com/question/11562149
Please help me with all asap I’ll mark brainly

Answers
The number of solution of each of the equations -2x + 4 = 4 - 2x, 5 - 3x = -5 - 3x and 2 + 3x = 2 + 2x are infinite solution, no solution and one solution respectively.
What is the number of solutions of each equation?Given the equations in the question;
a) -2x + 4 = 4 - 2x
b) 5 - 3x = -5 - 3x
c) 2 + 3x = 2 + 2x
To determine the number of solutions of each equation, solve for x.
a)
-2x + 4 = 4 - 2x
Solve for x
-2x + 2x + 4 - 4 = 4 - 4 - 2x + 2x
-2x + 2x = 4 - 4
0 = 0
Hence, the equation has infinite solutions.
b)
5 - 3x = -5 - 3x
Solve for x
5 - 5 - 3x + 3x = -5 - 5 - 3x + 3x
- 3x + 3x = -5 - 5
0 = -10
Hence, the equation has no solution.
c)
2 + 3x = 2 + 2x
Solve for x
2 - 2 + 3x - 2x = 2 - 2 + 2x - 2x
3x - 2x = 2 - 2
x = 0
Hence, the equation has one solution.
Learn to solve more equations here: https://brainly.com/question/9236233
#SPJ1
Solve this inequality 15n<8n-21
Answers
The solution of the inequality 15n>8n-21 is given by, n<-3.
Inequality is a relation between two or more mathematical expression or quantities via unequal signs i.e. greater, less, greater or equal, less or equal, not equal.
Given that the inequality is 15n<8n-21
Solving the inequality we have,
15n<8n-21
15n-8n<8n-21-8n, subtracting from both sides
7n<-21
n<-3, dividing 7 from both sides
So the solution of the given inequality is, n<-3.
To know more about Inequality refer to:
https://brainly.com/question/24372553
#SPJ1
Find the measure of ∠GJK. (I need the answer as fast as possible)

Answers
Answer:
∠ GJK = 102°
Step-by-step explanation:
(2x + 92) and (3x + 63) are same- side interior angles and sum to 180° , so
2x + 92 + 3x + 63 = 180
5x + 155 = 180 ( subtract 155 from both sides )
5x = 25 ( divide both sides by 5 )
x = 5
Then
∠ GJK = 2x + 92 = 2(5) + 92 = 10 + 92 = 102°
What are the rules of multiplying decimals?
Answers
Answer:
To multiply decimals, first multiply as if there is no decimal. Next, count the number of digits after the decimal in each factor. Finally, put the same number of digits behind the decimal in the product.
Step-by-step explanation:
1. Find the ratio of the area of two similar triangles if the ratioof two correspond side is 2:√3.
Answers
The ratio of the area of two similar triangles whose ratio of two correspond side is 2:√3 is; 4/3.
What is the ratio of ten areas?As evident in the task content; the two correspond side is 2:√3.
let k = ratio of two correspond sides.
Therefore, ratio of areas of the two triangles is; k².
Therefore, we have; 2² : (√3)².
Consequently, the ratio of the areas of the two triangles is; 4/3.
Read more on ratio of areas;
https://brainly.com/question/2254300
#SPJ1
Find the value of y
pls let me know how u solve this

Answers
Answer:
X° = 45°
Y = 8√2
Step-by-step explanation:
Angle of this triangle 45°:45°:90° so ratio of the triangle = 1:1:√2
8:8:8√2
I hope you understand it and sorry if it is wrong
7 more than a number ?
A)n+7
B)7+n
C)7-n
Answers
Answer:
B)7+n
Step-by-step explanation:
Answer:
A but see below.
Step-by-step explanation:
A is likely the best answer, although B is also correct. However you should write things in the other they are given.
n + 7 is the very best way to answer.
7 + n is not wrong but maybe not wanted.
As a general guideline, the research hypothesis should be stated as the _____. a. null hypothesis b. alternative hypothesis
c. hypothesis the researcher wants to disprove d. tentative assumption
Answers
As a general guideline, the research hypothesis should be stated as the B alternative hypothesis
What is a hypothesis?A statement of expectation or prediction that will be put to the test through research is called a research hypothesis. Learn more about the subject that interests you before developing your research hypothesis. A straightforward hypothesis is a claim that expresses the relationship between precisely two variables.
An assertion used in statistical inference experiments is known as the alternative hypothesis. Another way to put it is that it is just a different option from the null. An alternative theory in hypothesis testing is a claim that the researcher is testing.
Learn more about hypothesis on:
https://brainly.com/question/11555274
#SPJ1
A boat sails 6km from a point x on a bearing of 065 and thereafter 13km on a bearing of 136, what is the distance and of the boat from x?
Answers
Answer:
0650 + 500 = 1150
Step-by-step explanation:
You will need to represent the question on a triangle.
You will actually need a ruler and pencil for drawing along with a good eraser in case you make mistake.
Take your pencil and draw a point X, take ruler and rule a straight line to another point Y and rule another straight line to point Z and finally close it up at point X again.
A line passes through the points (-1,4) and (4,-2). Find the equation of the line in slope intercept form.
Answers
Answer:
Your Answer mark me as brainlist
Step-by-step explanation:
slope = "rise over run" the difference in y values divided by the difference in x values
= 6/-3 = -2 = m. It's negative because as x increases, y decreases
plug that into the point slope formula, with either point. generally use the most simple point
y-h= m(x-k) where m= -2 and (k,h) = (2,-2)
y+2 = -2(x-2)
simply if you want
Y = -2x +4 -2 = -2x +2
or
2x +y = 2
Wärmelehre - German
20 Words

Answers
Answer:
Step-by-step explanation:
a steel batch of t = 830 c is quenched in an oil bath (mol = 450kg / tol = 20c). What is the maximum mass of steel in kg allowed in the batch. Have the oil not heated up to more than 30 c?
useful data: ol c = 1.8kj / (kg.K)
steel: c = 0.49kj / (kg.K m steel = kg
A bacteria culture doubles every 5 hours. Determine the hourly growth rate of the bacteria
culture. Round your answer to the nearest tenth of a percent.
Answers
Answer:
10
Step-by-step explanation:
Using an exponential function, it is found that the hourly growth rate of the bacteria culture is of 14.9%.
------------------------
An exponential function has the following format:
\(A(t) = A(0)(1+r)^t\)
In which:
A(0) is the initial amount.r is the hourly growth rate.------------------------
Since it doubles every 5 hours, it means that:
\(A(5) = 2A(0)\)
And we use this to find r.
------------------------
\(A(t) = A(0)(1+r)^t\)
\(2A(0) = A(0)(1+r)^5\)
\((1 + r)^5 = 2\)
\(\sqrt[5]{(1 + r)^5} = \sqrt[5]{2}\)
\(1 + r = 2^{\frac{1}{5}}\)
\(1 + r = 1.149\)
\(r = 1.149 - 1 = 0.149\)
0.149*100% = 14.9%.
The hourly growth rate of the bacteria culture is of 14.9%.
A similar problem is given at https://brainly.com/question/24218305
Round 765.2 to nearest hundreds
Answers
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
Which best describes the graph of the cubic function f(x) = x3 + x2 + x + 1?
Answers
Answer:
Option A
Step-by-step explanation:
f(x) = x³ + x² + x + 1This is increasing function
The first option is correct
See attached graph for reference

Answer:
A
Step-by-step explanation:
That's your Danny had $20,000 to invest. He invest some of it in an account that paid 7% simple interest per year, and he invested the rest in an account that paid 10% simple interest per year. After one year, he received a total of $1580 in interest.how much did he invest in each account.first account $second account $
Answers
Let the principal of the investment be represnted below
\(p_1=20000-p_2\)Therefore,
\(\begin{gathered} I=\frac{prt}{100} \\ for\text{ the first one } \\ I=\frac{(20000-p_2)\times7\times1}{100}=\frac{140000-7p_2}{100} \\ \end{gathered}\)\(\begin{gathered} \text{For the second one} \\ I=\frac{p_2\times10\times1}{100}=\frac{10p_2}{100}=\frac{p_2}{10} \end{gathered}\)Therefore,
\(\begin{gathered} \frac{140000-7p_2}{100}+\frac{p_2}{10}=1580 \\ \frac{140000-7p_2+10p_2}{100}=1580 \\ 140000-7p_2+10p_2=158000 \\ 3p_2=158000-140000 \\ p_2=\frac{18000}{3} \\ p_2=6000 \end{gathered}\)\(\begin{gathered} P_1=20000-6000 \\ p_1=14000 \end{gathered}\)He invested $14000 in the first account and $6000 in the second account.