A baseball card that originally cost $24 has been decreasing in value
at an annual rate of 6% for the last 5 years. What is the present value?
Answers
Answer:
I believe it is four dollars
Related Questions
Find the slope of the tangent line to the given polar curve at the point specified by the value of θ. r = 4 sin θ, θ π/6
Answers
The slope of the tangent line to the given polar curve at the specified point is √3.
What is polar equation?
Cartesian coordinates, which may be found by moving across an x-axis and up and down the y-axis in a rectangular pattern, are complemented by polar coordinates. Polar coordinates are written as (r,) as opposed to the (x, y) used for Cartesian coordinates.
A point's location in polar coordinates is determined by its r from the origin and the angle θ (measured in radians) between the line leading to the point and the x-axis.
As given,
For the polar equation r = 4 sin θ, we have
x = r cosθ
x = 4 sinθ cosθ
x = 2sin2θ
y = r sinθ
y = 4 sin²θ
Differentiate obtained values of x and y with respect to θ respectively,
dx/dθ = d(2sin2θ)/dθ
dx/dθ = 2cos2θ (2)
dx/dθ = 4cos2θ
Similarly,
dy/dθ = d(4sin²θ)/dθ
dy/dθ = 4sin2θ
Evaluate the slope (dy/dx) as follows:
dy/dx = (dy/dθ) / (dx/dθ )
dy/dx = (4 sin2θ) / (4 cos2θ)
dy/dx = (sin2θ) / (cos2θ)
dy/dx = (tan2θ)
At θ = π/6
slope = dy/dx
Substitute values,
slope = tan2( π/6)
slope = tan( π/3)
slope = √3.
Hence, the slope of the tangent line to the given polar curve at the specified point is √3.
To learn more about polar coordinates from the given link.
https://brainly.com/question/14965899
#SPJ4
\(4.03 x 10x^{6}\)
Answers
The simplified form of the given expression 4.03x + 10x⁶, is \(x(4.03x + 10x^5)\)
What is an expression?An expression in math is a sentence with a minimum of two numbers or variables and at least one math operation.
Given that an expression 4.03x + 10x⁶
We need to simplify it,
4.03x + 10x⁶
Applying the exponent rule: \(a^{b+c}=a^ba^c\)
\(x^6=x^5x\)
\(=4.03x+10x^5x\)
Factor out common term x,
\(=x\left(4.03+10x^5\right)\)
Hence, the simplified form of the given expression 4.03x + 10x⁶, is \(x(4.03x + 10x^5)\)
Learn more about expressions, click;
https://brainly.com/question/14083225
#SPJ9
The quotient of a number and negative two is greater than or equal to ten
Answers
Answer:
n/-2 ≥ 10
Hope this helps!
Can somebody please help me? :(

Answers
Using the Distributive Property, we can simplify the equation \(2(3x + 4) = 6x + 8\) by multiplying 2 by each term inside the parentheses to get \(6x + 8.\)
What is the distributive Property?Isolate the variable: To isolate the variable in an equation means to rearrange the equation in such a way that the variable appears alone on one side of the equation.
For example, to isolate the variable n in the equation \(3n + 12 = 27,\) we can subtract 12 from both sides to get 3n = 15 and then divide both sides by 3 to get \(n = 5.\)
Inequality: An inequality is a mathematical statement that compares two expressions using one of the symbols <, >, ≤, or ≥. For example, \(3x + 5 < 10\) is an inequality that states that the expression \(3x + 5\) is less than 10.
Distributive Property: The Distributive Property is a property of multiplication that states that multiplying a number by a sum is the same as multiplying the number by each term in the sum and then adding the products.
For example, \(10(x + 5) = 10x + 50\) is an equation that uses the Distributive Property to simplify the expression \(10(x + 5)\) .
Example:
To isolate the variable in the equation \(4y - 6 = 18\), we can add 6 to both sides to get \(4y = 24\), and then divide both sides by 4 to get y = 6.
The inequality \(2x + 3 > x + 7\) states that the expression \(2x + 3\) is greater than x + 7.
Therefore, Using the Distributive Property, we can simplify the equation \(2(3x + 4) = 6x + 8\) by multiplying 2 by each term inside the parentheses to get \(6x + 8\).
Learn more about property here:
https://brainly.com/question/5637942
#SPJ1
when you solve a system of equations (i.e. two equations with two variables each), what possible form(s) could the solution take
Answers
. A(0,8), B(6,5), C(-3,2)
Answers
Answer:
a
Step-by-step explanation:
Use linear approximation, i.e. the tangent line, to approximate as follows: Let f(x) = and find the equation of the tangent line to f(x) at a nice" point near 0.202. Then use this to 1/0.202 approximate 1/0.202

Answers
ANSWER
\(\begin{equation*} 4.95 \end{equation*}\)EXPLANATION
Given;
\(f\mleft(x\mright)=\frac{1}{x}\)Now, evaluate its first derivative;
\(f^{\prime}(x)=-\frac{1}{x^2}\)Now;
\(\begin{gathered} x=0.2=\frac{1}{5} \\ f(x)=5,f^{\prime}(x)=-25 \end{gathered}\)Hence, we have;
\(l(x)=5-25(x-0.2)=5-25x+5\)by substitution;
\(\begin{gathered} \frac{1}{0.202}=5.25(0.202-0.2) \\ =5-0.05 \\ \cong4.95 \end{gathered}\)
Use the drawing tool(s) to form the correct answer on the provided grid.
A team of painters is working on the exterior of a building. One of the painters sets a ladder on the ground 5 feet from the base of the building
and leans it up to touch the wall. Using an angle measurement tool, he finds that the angle the ladder makes with the ground is 73.61 degrees.
Use the grid provided to draw a scale representation of the ladder against the wall, rounding calculations to the nearest foot. Each unit on the
grid represents one foot. i’m
Answers
The Length of ladder is 17.73 feet.
What is angle of elevation?The angle formed by the line of sight and the horizontal plane for an object above the horizontal.
distance of the foot of the ladder = 5 feet
Using trigonometry,
cos \(\theta\\\) = B/H
cos 73.61= 5/H
0.282 = 5/H
H = 5/0.282
H = 17.73 feet
Learn more about this concept here:
https://brainly.com/question/13193897
#SPJ1
3|2+x|-4=14
Solve this absolute value equation.
Answers
Answer:
Its a number
Step-by-step explanation
Consider a piece of wire with uniform density. It is the quarter of a circle in the first а quadrant. The circle is centered at the origin and has radius 3. Find the center of gravity
Answers
To find the center of gravity of the wire, we need to use the formula for center of gravity of a two-dimensional object:
x-bar = (1/A) ∫y*dA
y-bar = (1/A) ∫x*dA
where A is the area of the object, x and y are the coordinates of any point on the object, and the integrals are taken over the entire area of the object.
Since the wire is a quarter of a circle in the first quadrant with radius 3, the area of the wire is:
A = (1/4)π(3^2) = (9/4)π
To find the center of gravity, we need to split the wire into small elements and integrate over the entire area. We can use polar coordinates to simplify the integration. Let r be the distance from the origin to a point on the wire, and θ be the angle that the radius makes with the x-axis. Then the coordinates of any point on the wire are:
x = r*cos(θ)
y = r*sin(θ)
Since the wire has uniform density, the mass of each element is proportional to its length. The length of each element is equal to the radius times the angle it subtends at the center of the circle, which is dθ. So the mass of each element is:
dm = ρ*r*dθ
where ρ is the density of the wire.
To find the center of gravity in the x-direction, we integrate over the x-coordinates of each element:
x-bar = (1/A) ∫y*dA
x-bar = (1/A) ∫[r*sin(θ)]*dm
x-bar = (1/A) ∫[r*sin(θ)]*ρ*r*dθ
x-bar = (1/A) ∫(3*sin(θ))*(ρ*r^2)*dθ
x-bar = (1/(9/4)π) ∫(3*sin(θ))*(ρ*r^2)*dθ
x-bar = (4/9) ∫(3*sin(θ))*(ρ*r^2)*dθ
x-bar = (4/9) ρ ∫(3*sin(θ))*(r^2)*dθ
x-bar = (4/9) ρ ∫(3*sin(θ))*(r^3)*(dθ/r)
x-bar = (4/9) ρ ∫(3*sin(θ))*(r^2)*dr
x-bar = (4/9) ρ ∫(9*cos(θ))*(r^2)*dr
x-bar = (4/9) ρ [∫(9*r^2*cos(θ))*dr]
x-bar = (4/9) ρ [(9/3)*r^3*cos(θ)]
x-bar = (4/3) ρ r^3*cos(θ)
The limits of integration for θ are from 0 to π/2, since the wire is in the first quadrant. Substituting r=3 and ρ=1 (since the wire has uniform density), we get:
x-bar = (4/3) (3^3) ∫cos(θ)*dθ
x-bar = 36 ∫cos(θ)*dθ
x-bar = 36 [sin(θ)]_0^π/2
x-bar = 36 [sin(π/2) - sin(0)]
x-bar = 36
Therefore, the center of gravity of the wire is located at (36, 0).
Learn more about :
gravity : brainly.com/question/14874038
#SPJ11
help xxx
23421 x 230 = ? im not allowed to use a calc on this
Answers
Answer:
5,386,830
Step-by-step explanation:
Find the Area of the figure below, composed of a square and four semicircles. Rounded to the nearest tenths place
12
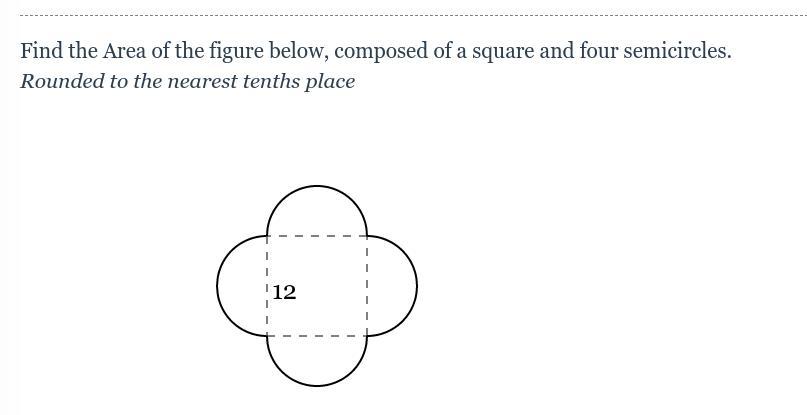
Answers
Answer:
370.1 \(units^{2}\)
Step-by-step explanation:
Square
a = \(s^{2}\)
a = \(12^{2}\) = 144
Semi - Circle:
a = 1/2(\(\pi r^{2}\))
a = 1/2(3.14)(36) The radius is 1/2 the diameter of 12 (6) \(6^{2}\) = 36
a = 1/2(113.04)
a = 56.52
144 + 4(56.52)
144 + 226.08
370.08 rounded to the nearest tenths place 370.1
The point-slope form of the equation of the line that passes through (-9, -2) and (1, 3) is y - 3 = {(x :- 1). What is
the slope-intercept form of the equation for this line?
y= {x + 2
O y= {x-4
O y = 2/ 3x + 3/2
O y = 2 / 3x - 2 / 2
Answers
Answer:
Its B because its saids y equal times what plus 2 so you have to figure that out i got my answer.
A loan of $3000 is to be repaid in four equal semiannual (every 6 months) payments. If the annual interest rate is 8% compounded semiannually, how much is each payment? 3. A machine costs $30,000 and has a 6-year useful life. At the end of the 6 years, it can be sold for $9,000. If annual interest is 8%, compounded semiannually, what is the equivalent uniform annual cost of the machine?
Answers
Loan repayment: Each semiannual payment is $879.92.
Machine cost: The equivalent uniform annual cost is $6,541.34.
Loan Repayment:
1. Calculate the semiannual interest rate: Divide the annual interest rate (8%) by the number of compounding periods per year (2) to get the semiannual interest rate (4%).
2. Calculate the number of compounding periods: Since the loan is repaid in four equal semiannual payments, there are a total of eight compounding periods (4 years x 2).
3. Calculate the present value factor: Use the formula for the present value of an annuity to calculate the present value factor for eight periods at a semiannual interest rate of 4%.
4. Determine the payment amount: Divide the loan amount ($3000) by the present value factor from step 3 to find the equal semiannual payment.
Machine Cost:
1. Calculate the semiannual interest rate: Divide the annual interest rate (8%) by the number of compounding periods per year (2) to get the semiannual interest rate (4%).
2. Calculate the number of compounding periods: Since the useful life of the machine is 6 years and compounding occurs semiannually, there are a total of 12 compounding periods (6 years x 2).
3. Calculate the future value factor: Use the formula for the future value of a single sum to calculate the future value factor for 12 periods at a semiannual interest rate of 4%.
4. Determine the equivalent uniform annual cost: Subtract the future value of the machine ($9,000) from the initial cost of the machine ($30,000) and divide by the future value factor from step 3 to find the equivalent uniform annual cost.
By following these steps and performing the calculations, you will determine the semiannual payment for the loan and the equivalent uniform annual cost of the machine.
To learn more about loan, click here: brainly.com/question/25696681
#SPJ11
Pls help me. To be submitted tomorrow

Answers
Answer:
\(\frac{1}{7}\)
Step-by-step explanation:
Given
tanx = \(\frac{3}{4}\) = \(\frac{opposite}{adjacent}\)
This is a 3- 4- 5 right triangle with hypotenuse = 5, then
cosx = \(\frac{adjacent}{hypotenuse}\) = \(\frac{4}{5}\)
sinx = \(\frac{opposite}{hypotenuse}\) = \(\frac{3}{5}\)
Then
\(\frac{cosx-sinx}{cosx+sinx}\)
= \(\frac{\frac{4}{5}-\frac{3}{5} }{\frac{4}{5}+\frac{3}{5} }\)
= \(\frac{\frac{1}{5} }{\frac{7}{5} }\)
= \(\frac{1}{5}\) × \(\frac{5}{7}\)
= \(\frac{1}{7}\)
Write 7/13 as a decimal to the hundredths place and write the remainder as a fraction.
Answers
7/13 as a decimal to the hundredths place is 0.54 and the remainder as a fraction is 7/13.
7/13 as a decimal to the hundredths place and the remainder as a fraction
In order to convert 7/13 to a decimal, we will divide 7 by 13.
Using long division, we get7 ÷ 13 = 0.53846153846...To the nearest hundredth, we round up to 0.54.
Hence, 7/13 as a decimal to the hundredths place is 0.54.
To find the remainder as a fraction, we subtract the product of the quotient and divisor from the dividend. Then, we simplify the fraction as much as possible.
Remainder = Dividend - Quotient x DivisorRemainder = 7 - 0 x 13
Remainder = 7/13
Therefore, 7/13 as a decimal to the hundredths place is 0.54 and the remainder as a fraction is 7/13.
To know more about fraction visit:
https://brainly.com/question/10354322
#SPJ11
which number is equivalent to
6^2×6^3
A. 150
B. 623
C. 327
D. 252
Answers
Answer:
150
Step-by-step explanation:
In a statistical test of hypotheses, we say the data are statistically significant at level α if.
Answers
If the P value in a statistical test of hypotheses is more than, we may claim that the data are statistically significant at level. Less than is the P-value. =0.05 .
What is hypotheses ?An assumption is said to as a hypothesis when it is supported by evidence. Any investigation that turns the research questions into predictions must start here. Variables, the population, and the relationships between the variables are among its constituent parts. A hypothesis used to examine the link between two or more variables is known as a research hypothesis.
One dependent variable and one independent variable are shown to be related. For instance, eating more vegetables will help you lose weight more quickly. In this scenario, increasing your vegetable intake is an independent variable, while weight loss is the dependent variable.
It makes a claim that conflicts with the premise. There is no connection between the independent and dependent variables, which is a negative assertion. The emblem stands for.
Hence, If the P value in a statistical test of hypotheses is more than, we may claim that the data are statistically significant at level. Less than is the P-value. =0.05 .
learn more about hypothesis click here:
https://brainly.com/question/606806
#SPJ4
ASAP, Will give you the brainliest answer. Thanks
Enlarge shape A by scale factor 2 with centre of enlargement (-2, -5).
What are the coordinates of the vertices of the image?

Answers
The coordinates of the image of the shape A with vertices at (2, 3), (4, 7), (8, 3), and (-2, -5) enlarged by a scale factor 2 with centre of enlargement at (-2, -5) are (0, -1), (2, 1), (4, -1), and (-4, -9).
Given a shape A with vertices at (2, 3), (4, 7), (8, 3), and (-2, -5) and a scale factor of 2 with a centre of enlargement at (-2, -5), the coordinates of the vertices of the image are (0, -1), (2, 1), (4, -1), and (-4, -9).
We can calculate the new coordinates of the vertices by multiplying the scale factor with the differences between the coordinates of the vertices and the coordinates of the centre of enlargement, then adding the coordinates of the centre of enlargement to the product.
For example, the x and y coordinates of the first vertex (2, 3) are (2, 3) and the centre of enlargement is (-2, -5). So, the difference between the two is (2 - (-2), 3 - (-5)) = (4, 8). Multiplying the scale factor 2 with the differences gives (4 * 2, 8 * 2) = (8, 16). Adding the centre of enlargement to the product gives (8 + (-2), 16 + (-5)) = (6, 11). Therefore, the coordinates of the image of the first vertex is (6, 11).
Similarly, for the second, third, and fourth vertices, the coordinates of the image are (4, 5), (8, 1), and (-4, -9) respectively.
Learn more about coordinates here:
https://brainly.com/question/16634867
#SPJ1
Express ln 32 - ln 8 as a single natural logarithm. Ln 4 ln 24 ln 256.
Answers
\(\textit{Logarithm of rationals} \\\\ \log_a\left( \frac{x}{y}\right)\implies \log_a(x)-\log_a(y) \\\\[-0.35em] ~\dotfill\\\\ \ln(32)-\ln(8)\implies \ln\left( \cfrac{32}{8} \right)\implies \ln(4)\)
Answer:
Next one is (B) In 4
Step-by-step explanation:
EDGE 2022
five cards are drawn at random and without replacement from an ordinary deck of cards. let x1 and x2 denote, respectively, the number of spades and the number of hearts that appear in the five cards. (a) determine the joint pmf of x1 and x2. (b) find the two marginal pmfs. (c) what is the conditional pmf of x2, given x1
Answers
There are (525) possible combinations of 5 cards, and each combination has an equal chance of being drawn.
What is probability?The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a statement is true.An event's probability is a number between 0 and 1, where, roughly speaking, 0 denotes the event's impossibility and 1 denotes certainty.The likelihood that an event will occur increases with its probability.A straightforward illustration is tossing a fair (impartial) coin.The chance of both outcomes ("heads" and "tails") is equal because the coin is fair, "heads" is more likely than "tails," there are no other conceivable outcomes, and the likelihood of either outcome is .According to our question-
It is simpler to derive this from first principles than to add up the x2 (which will work but is harder).
There are (525) possible combinations of 5 cards, and each combination has an equal chance of being drawn.
The number of combinations that contain x1 spades is what we are looking for.
There are (13x1) ways to select the spade, followed by (395x1) ways to select the other card.
Hence, There are (525) possible combinations of 5 cards, and each combination has an equal chance of being drawn.
learn more about probability click here:
brainly.com/question/13604758
#SPJ4
If you know the length of an object in centimeters, how can you
figure out the length of the object in millimeters without re measuring
Answers
Answer:
There are 10 mm in a cm so if u have let's say 5 cm than u would have 50mm
Find all the real values of x such that f(x)=0. f(x)=4x+34
Answers
EXPLANATION
If f(x) = 4x + 34, the values of x such that f(x) = 0 can be obtained by equaling the function to zero as shown as follows:
4x + 34 = 0
Subtracting -34 to both sides:
4x = -34
Dividing both sides by 4:
x = -34/4
Simplifying:
x = -8.5
Hence, the value is x=-8.5
In both the Vendor Compliance at Geoffrey Ryans (A) and
Operational Execution at Arrows Electronics there are problems and
challenges. Integrate the problems and challenges from both
cases.
Answers
In both the Vendor Compliance at Geoffrey Ryans (A) and Operational Execution at Arrows Electronics cases, there are common problems and challenges. These include issues related to vendor management.
One of the key problems faced by both companies is vendor compliance. This refers to the ability of vendors to meet the requirements and standards set by the company. Both cases highlight instances where vendors fail to meet compliance standards, leading to disruptions in the supply chain and operational inefficiencies. This problem affects the overall performance and profitability of the companies.
Another challenge faced by both companies is operational execution. This encompasses various aspects of operations, including inventory management, order fulfillment, and delivery. In both cases, there are instances where operational execution falls short, leading to delays, errors, and customer dissatisfaction. This challenge requires the companies to streamline their processes, improve communication and coordination, and enhance overall operational efficiency.
Overall, the problems and challenges in both cases revolve around effective vendor management, supply chain optimization, and operational excellence. Addressing these issues is crucial for both companies to improve their performance, meet customer demands, and maintain a competitive edge in the market.
To learn more about vendor management click here :
brainly.com/question/30714854
#SPJ11
Use the simplex algorithm to find the optimal solution to the following LP (solve manually): maxz= 36x1+30x2−3x3−4x4
s.t. x1+x2−x3≤5
6x1+5x2−x4≤10
∀xi≥0
Answers
The maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
maximize: z = c1x1 + c2x2 + ... + cnxn
subject to
a11x1 + a12x2 + ... + a1nxn ≤ b1
a21x1 + a22x2 + ... + a2nxn ≤ b2
am1x1 + am2x2 + ... + amnxn ≤ bmxi ≥ 0 for all i
In our case,
the given LP is:maximize: z = 36x1 + 30x2 - 3x3 - 4x
subject to:
x1 + x2 - x3 ≤ 5
6x1 + 5x2 - x4 ≤ 10
xi ≥ 0 for all i
We can rewrite the constraints as follows:
x1 + x2 - x3 + x5 = 5 (adding slack variable x5)
6x1 + 5x2 - x4 + x6 = 10 (adding slack variable x6)
Now, we introduce the non-negative variables x7, x8, x9, and x10 for the four decision variables:
x1 = x7
x2 = x8
x3 = x9
x4 = x10
The objective function becomes:
z = 36x7 + 30x8 - 3x9 - 4x10
Now we have the problem in standard form as:
maximize: z = 36x7 + 30x8 - 3x9 - 4x10
subject to:
x7 + x8 - x9 + x5 = 5
6x7 + 5x8 - x10 + x6 = 10
xi ≥ 0 for all i
To apply the simplex algorithm, we initialize the simplex tableau as follows:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0 | 36 | 30 | -3 | -4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | 0 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x6| 0 | 0 | 1 | 6 | 5 | 0 | -1 | 10 |
---------------------------------------------------------------------------
Now, we can proceed with the simplex algorithm to find the optimal solution. I'll perform the iterations step by step:
Iteration 1:
1. Choose the most negative coefficient in the 'z' row, which is -4.
2. Choose the pivot column as 'x10' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 5/0 = undefined, 10/(-4) = -2.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to
make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.4 | 36 | 30 | -3 | 0 | 12 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.2 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x10| 0 | 0 | 0.2 | 1.2 | 1 | 0 | 1 | 2.5 |
---------------------------------------------------------------------------
Iteration 2:
1. Choose the most negative coefficient in the 'z' row, which is -3.
2. Choose the pivot column as 'x9' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 12/(-3) = -4, 5/(-0.2) = -25, 2.5/0.2 = 12.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.8 | 34 | 30 | 0 | 4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.4 | 0.6 | 1 | 5 | -2 | 10 |
---------------------------------------------------------------------------
x9| 0 | 0 | 1 | 6 | 5 | 0 | -5 | 12.5 |
---------------------------------------------------------------------------
Iteration 3:
No negative coefficients in the 'z' row, so the optimal solution has been reached.The optimal solution is:
z = 0
x1 = x7 = 0
x2 = x8 = 10
x3 = x9 = 0
x4 = x10 = 0
x5 = 10
x6 = 0
Therefore, the maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
Learn more about Simplex Algorithm here:
https://brainly.in/question/46895640
#SPJ11
Solve a = d+c/b
Help me please

Answers
Answer:
Option A is the correct
Step-by-step explanation:
a=d+c/b
Now we have to solve for d
Multiplying b on both sides
a*b=d+c/b*b
ab=d+c
ab-c=d
I hope this will help you:)
Which of the following values is the solution to the equation
-16 + x = -30 ?
1.)-2
2.)-14
3.)-480
4.)-46
Answers
Answer:
Step-by-step explanation:
x - 16 = -30
x = -14
Answer:
3.
Step-by-step explanation:-16 + x = -30
what is the measure of GAB
Answers
Answer:
180°
Step-by-step explanation:
the measure of GAB is 180°
Answer:
TRUBOMAT GAB measures the turbidity of liquid applying nephelometric method. For this purpose, a combined transmitted & scattered beams measurements are used, in which a transmitter and a receiver face each other and another transmitter is arranged orthogonally (at an angle of 90 °).
please mark as brainliest
For A-D, choose Yes or No to indicate whether the situation can be represented by a negative number.
A. A student answered a 5-point question correctly.
B. Mila lost 30 points answering a question incorrectly.
C. A dog loses 13 pounds.
D. The average temperature in a city last month was 68°F.
OYes No
OYes No
OYes No
OYes No
Answers
Answer:
A. NO
B. YES
C: YES
D: NO
Step-by-step explanation:
HELP NEEDED ASAP/NOW......NO LINKS AND NO JOKING PLS
AUBSERD ANSWERS WILL BE REPORTED
Give the answer as a simplified expression written in descending order.
A) f(x+1)=7(x+1)-3
B) f(-x)=7(-x)-3
Answers
Evaluating the function as simplified expression, we have:
A. f(x + 1) = 7x + 7 - 3
B. f(-x) = -7x - 3
How to Evaluate a Function?To state the simplified form of each of the given functions in descending order, implies that we are to leave our answer in the standard form.
A. f(x + 1) = 7(x + 1) - 3
Apply the distributive property
f(x + 1) = 7(x) + 7(1) - 3
f(x + 1) = 7x + 7 - 3
Combine like terms
f(x + 1) = 7x + 4 [descending order/standard form]
B. f(-x) = 7(-x) - 3
Simplify
f(-x) = -7x - 3 [descending order/standard form]
Therefore, evaluating the function as simplified expression, we have:
A. f(x + 1) = 7x + 7 - 3
B. f(-x) = -7x - 3
Learn more about functions on:
https://brainly.com/question/15602982
#SPJ1