A bacteria culture starts with 6,500 bacteria. After 2. 5 hours, there are 208,000 bacteria present. What is the length of the doubling period
please lmk how you got the answer i’m confused
Answers
The doubling period of the bacteria in the culture is 3 hours.
What is exponential growth?Exponential growth refers to a sort of function in which the growth is modelled by an exponential function. The growth of the organisms in this culture is modelled by the equation; P(t) = Poe^rt
Where;
P(t) = population at time t
Po = initial population
r = growth rate
t = time taken
Now;
208,000 = 6,500e^2.5r
208,000/ 6,500 = e^2.5r
ln(208,000/ 6,500) = ln (e^2.5r)
3.46 = 2.5 r
r = 3.46/2.5
r = 1.38 hr-1
If the population is doubled, we have 416000
416000 = 6,500e^(1.38t)
416000/6,500 = e^(1.38t)
64 = e^(1.38t)
ln(64) = lne^(1.38t)
4.15 = 1.38t
t = 4.15 / 1.38
t = 3 hours
Learn more about exponential growth: https://brainly.com/question/1340582
Related Questions
HELPPPP
What is the equation, in slope-intercept form, of the line that passes through
the point (7, 2) and is parallel to y= -2x+1?
Answers
Find the slope of the parallel line
(7, 2) and is parallel to y= -2x+1?
When two lines are parallel, they have the same slope.
⇒ if the slope of the given line is = - 2
then the slope of the parallel line (m) = - 2
Determine the equation
We can now use the point-slope form (y - y₁) = m(x - x₁)) to write the equation for this line:
⇒ y - 2 = - 2 (x - 7)
We can therefore write the equation in the slope-intercept form by making y the subject of the equation and expanding the bracket to simplify:
since y - 2 = - 2 (x - 7)
∴ y = - 2 x + 16
!) What does the double line connected to the double diamond symbol indicate? (mark all that apply):A) Partial participation between associated entities.B) Total participation between associated entities.C) That the double rectangle entity can not exist without the single rectangle entity connected to it.D) That the double rectangle entity can exist without the single rectangle entity connected to it.E) That the single rectangle entity can not exist without the double rectangle entity connected to it.
Answers
The double line connected to the double diamond symbol indicates:
B) Total participation between associated entities. ,and,
C) That the double rectangle entity can not exist without the single rectangle entity connected to it.
The double line connected to the double diamond symbol indicates that total participation between associated entities and that the double rectangle entity can not exist without the single rectangle entity connected to it. The reason behind it is that Double diamonds are always used to represent relationships between strong and weak entities. Strong Entity - Simple Rectangle Weak Entity - Double Rectangle.
An Entity Relationship diagram (ER) is a data modeling diagram used to represent the entities that will be modeled in a database, and the relationships between those entities (I use the one-to-many, one-to-one , many-to-many relationship terms themselves). When implementing a relational database, these relationships will determine which foreign keys I need to implement to relate one table to another. Diamonds represent sets of relationships in an ER diagram. A relationship set defines the relationship between two sets of entities in a database. A double diamond represents a set of relationships linked to a set of weak entities. A set of weak entities is a collection without a primary key.
Learn more about Rectangle:
https://brainly.com/question/28993977
#SPJ4
whats the height of the prism
if you can help me with is question it would mean a lot :) im having some trouble figuring it out
Iready
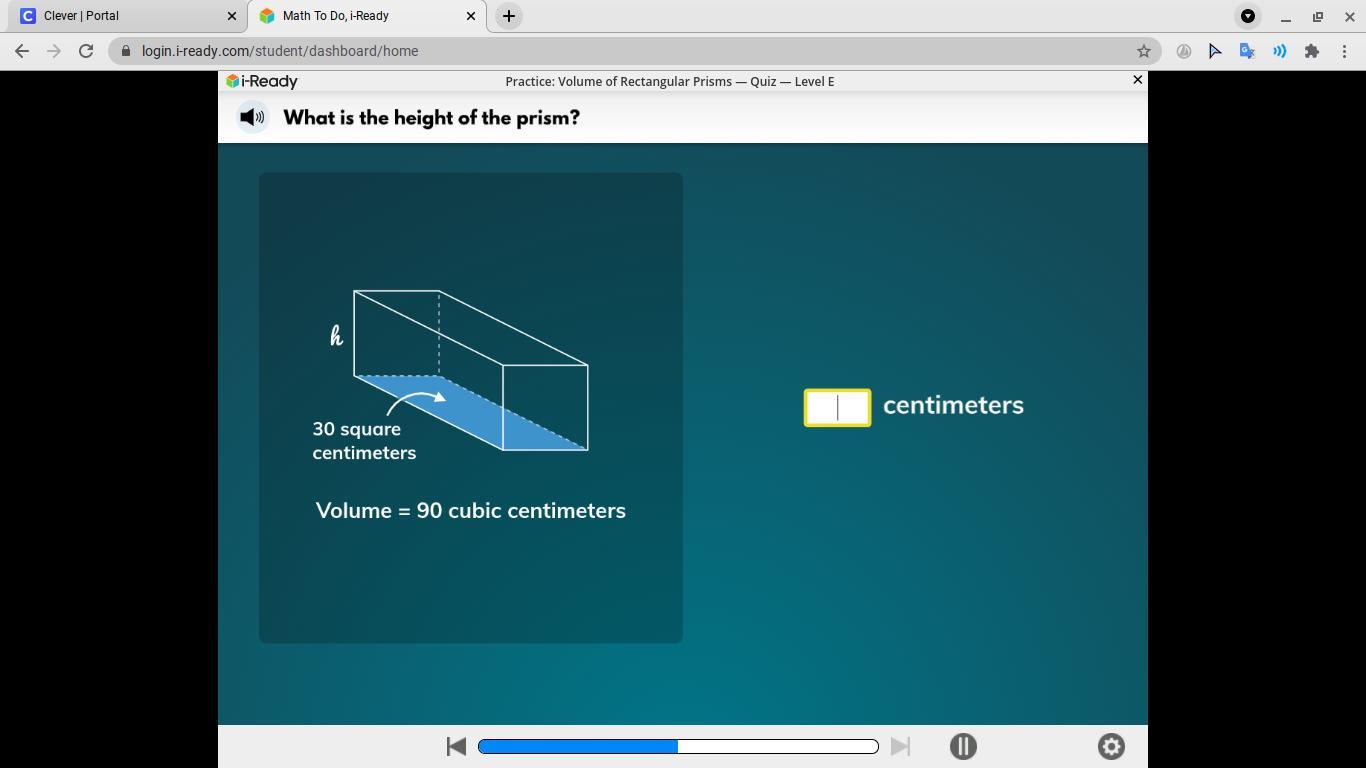
Answers
Answer:
The height of the prism = 3cm
Step-by-step explanation:
Answer:3
Step-by-step explanation:
The base of the solid is square, one of whose sides is the interval [0, 2] along the the x-axis. The cross sections perpendicular to the x-axis are rectangles of height f(x) 8x² . Compute the volume of the solid. (Use symbolic notation and fractions where needed:)
Answers
The volume of the solid is 64/3 cubic units.
To compute the volume of the solid, we integrate the area of the cross sections over the interval [0, 2] along the x-axis. The area of each cross section is given by the product of the height f(x) = 8x² and the width dx. Hence, we have:
V = ∫[0,2] f(x) dx
= ∫[0,2] 8x² dx
= [8(x³/3)] [0,2]
= 8(2³/3 - 0³/3)
= 8(8/3)
= 64/3
Therefore, the volume of the solid is 64/3 cubic units.
Learn more about volume here
https://brainly.com/question/27710307
#SPJ11
Which of the following BEST describes how to use the addition property of equality to isolate the variable
m below?
-6 = -3+ m
A. add 3 to both sides of the equation
B. subtract 3 from both sides of the equation
C. add 6 to both sides of the equation
D. subtract 6 from both sides of the equation
Answers
Answer:B
Step-by-step explanation:
From calculating the equations below, we find that all sections have m equal to negative three.
According to the second option, it is most likely because six is added.
Elizabeth is considering buying a $30,000 car. Which financing option would
have the LOWEST expected monthly payment and the HIGHEST expected total
interest payments? *
$0 down payment, 6% interest, 60 months
$0 down payment, 6% interest, 84 months
$3000 down payment, 6% interest, 60 months
$3000 down payment, 0% interest, 36 months
Answers
The lowest expected monthly payment and the highest expected total
interest payments will be $0 down payment, 6% interest, 84 months.
What is down payment?In a financial transaction, such as the purchase of a property or car, a down payment is cash given up ahead.Loans are frequently obtained by buyers to cover the remaining balance of the purchase price.The more money the buyer puts down, the less they'll need to borrow to complete the deal, the lower their monthly payments, and the less interest they'll end up paying overall.Lenders may ask for down payments of 0% or even 50%, depending on the borrower and the type of transaction.A down payment on a property is a typical illustration of a down payment. The down payment for a home can range from 5% to 25%, with the remaining amount being covered by a mortgage obtained from a bank or another financial institution. Car down payments function similarly.The down payment may not always be refunded if the buyer causes the contract to fall through.To learn more about down payment, refer to
https://brainly.com/question/1698287
#SPJ4
Which expression completes the statement to form a true equation?
28–3+2=
3³
5(4 + 2)
3² + 19
44–24
Please help!
Answers
Central Market sells 5 jars of jam for $3.00. Valley Market sells jars of jam at 59 cents per jar. Yasmin bought 10 jars from Central Market, and Nadia bought 10 jars from Valley Market.
Answers
Answer:
Yasmin will spend $6
Nadia will spend $5.9
Step-by-step explanation:
Step one:
the cost of 5 jars at Central market is $3
the cost of 1 jar = 3/5= $0.6
60 cents per jar
we are told that Valley Market sells jars of jam at 59 cents per jar.
$0.59
Step two:
If Yasmin buys 10 jars from Central Market,
Yasmin will spend = 10*0.6= $6
If Nadia buys 10 jars from Valley Market.
Nadia will spend = 10*0.59= $5.9
The market difference is 6-5.9= $0.1
ten percent of the items produced by a machine are defective. out of 15 items chosen at random, what is the probability that exactly 3 items will be defective?
Answers
The probability of exactly 3 items out of 15 being defective is 0.184 or approximately 18.4%.
What is Probability ?
Probability can be defined as ratio of number of favourable outcomes and total number outcomes.
To solve this problem, we can use the binomial distribution, which is a probability distribution that describes the number of successes in a fixed number of independent trials, where each trial has the same probability of success.
In this case, the probability of a single item being defective is 10%, or 0.1, and the probability of a single item being non-defective is 90%, or 0.9. We want to know the probability of getting exactly 3 defective items out of a sample of 15 items.
Using the binomial distribution formula, we can calculate this probability as follows:
P(X = 3) = (15 choose 3) * \(0.1^3\) *\(0.9^12\)
where (15 choose 3) is the number of ways to choose 3 items out of 15, which is given by the binomial coefficient:
(15 choose 3) = 15! / (3! * 12!) = 455
Substituting these values into the formula, we get:
P(X = 3) = 455 * \(0.1^3\) *\(0.9^12\)
Therefore, the probability of exactly 3 items out of 15 being defective is 0.184 or approximately 18.4%.
To learn more about Probability from given link.
brainly.com/question/30034780
#SPJ1
Choose the polynomial written in standard form. x2 4x4 10x6 x4 4x3 10x x7 4x3 10x4 x6 4x3 10x7
Answers
The polynomial that is written in standard form out of the given options is given by: Option 2: x^4 + 4x^3 + 10x
What is standard form of a polynomial?Suppose the considered polynomial is of only one variable.
Then, the standard form of that polynomial is the one in which the terms with higher exponents are written on left side to those which have lower exponents.
What are terms in polynomials?Terms are added or subtracted to make a polynomial. They're composed of variables and constants all in multiplication.
Example:
\(x^3 + 3x +5\)
is a polynomial consisting 3 terms as \(x^3, 3x \: \rm and \: 5\)
Cheking all the options for them being in standard form or not:
Option 1: \(x^2 + 4x^4 + 10x^6\)Second term has 4 as exponent, but on its left, the first term has 2 as exponent. So higher expoent holding term is not on left. Thus, this polynomial is not in standard form.
Option 2: \(x^4 + 4x^3 + 10x\)4 > 3 > 1 (comparing the exponents), and the terms holding them are also in this order (left to right).
Thus, this polynomial is in standard form.
Option 3: \(x^7 + 4x^3 + 10x^4\)Not in standard form because the last term has bigger power then the term on its left.
Option 4: \(x^6 + 4x^3 + 10x^7\)Not in standard form because the last term has bigger power then the term on its left.
Thus, the polynomial that is written in standard form out of the given options is given by: Option 2: x^4 + 4x^3 + 10x
Learn more about standard form of a polynomial here:
https://brainly.com/question/15313798
The boys football team is selling game tickets for a football game. Adult admission is $8 and student admission is $6 there are usually twice as many students than adults at the game. If the goal is to make $3000. Write 2 equations. Solve the system of equations, how many student and adult tickets must be sold? Let a = the number of adults and b = the number of students
Answers
To make $3000 selling game tickets, the boys football team needs to sell a combination of adult and student tickets. Solving the system of equations gives the number of adult and student tickets that must be sold 150 adult tickets and 300 student tickets.
The first equation relates the number of adults and students: since there are twice as many students as adults, we can write
b = 2a
where b is the number of students and a is the number of adults.
The second equation relates the revenue from ticket sales to the number of adults and students
8a + 6b = 3000
where 8a is the revenue from adult tickets and 6b is the revenue from student tickets.
Now we can substitute the first equation into the second equation to get
8a + 6(2a) = 3000
Simplifying, we get
20a = 3000
Dividing by 20, we get
a = 150
This means we need to sell 150 adult tickets. Using the first equation, we can find the number of student tickets
b = 2a = 2(150) = 300
So we need to sell 300 student tickets.
Therefore, the boys football team must sell 150 adult tickets and 300 student tickets to reach their goal of making $3000.
To know more about system of equations:
https://brainly.com/question/21620502
#SPJ1
A street light is 7.5 feet tall casts a 3-foot-long shadow A nearby flagpole casts a 16.5 foot long shadow what is the height of the flag pole
Answers
Answer:
h = 41.25 foot
Step-by-step explanation:
Given that,
Height of a street light = 7.5 feet
It casts a 3-foot-long shadow.
A nearby flagpole casts a 16.5 foot long shadow. We need to find the height of the flag pole. Let the height be h. It can be calculated as :
\(\dfrac{\text{height of street light}}{\text{height of shadow of street light}}=\dfrac{\text{height of flagpole}}{\text{height of shadow of the flag pole}}\\\\\dfrac{7.5}{3}=\dfrac{h}{16.5}\\\\h=\dfrac{7.5\times 16.5}{3}\\\\h=41.25\ foot\)
So, the height of the flag pole is equal to 41.25 foot.
The height of the flag pole is 41.25 feet tall.
Word problems in mathematics are methods used to solve real-life cases. They usually follow a logical approach with the use of arithmetic operations when solving them.
From the parameters given:
If 7.5 feet tall casts = 3-foot long shadowLet the height of the flag pole be = x
∴
(x) feet tall casts = 16.5 foot long shadow.To determine the height of the flag pole, we have:
\(\mathbf{x = \dfrac{7.5 feet \ tall \times 16.5 \ foot \ long} {3 \ foot \ long} }\)
x = 41.25 feet tall
Learn more about word problems here:
https://brainly.com/question/21405634
I need help plz help me I am not good at math HELP

Answers
Answer:
600 boys
800 girls
Step-by-step explanation:
Ratio is 3:4
let total number of boys be x
3/4=x/1400-x
4x=3(1400-x)
4x=4200-3x
7x=4200
x=600
600 boys
1400-600 = 800 girls
3 2/5 times 2 1/3 simplified answer pls
Answers
Exact: 119/15
Look at the figure. Classify the pair of angles: <2 and <7.
•corresponding angles
•same-side interior angles
•same-side exterior angles
•alternate interior angles

Answers
Answer:
Same-side exterior angles
Step-by-step explanation:
Through the process of elimination it is not:
→ Corresponding angles as that would be 2 and 6
→ Same side interior angles as that would be 3 and 6 or 4 and 5
→ Alternate interior angles as that would be 6 and 4 of 3 and 5
the probability of winning on a slot machine game is 0.152. if you play the slot machine until you win for the first time, what is the expected number of games it will take?
Answers
The expected number of games it will take to win on a slot machine game with a probability of winning of 0.152 is approximately 6.579 games.
The expected number of games can be calculated using the formula for the expected value of a geometric distribution. In this case, the probability of winning on each game is 0.152.
The expected number of games is calculated as the reciprocal of the probability of winning. Therefore, the expected number of games is 1 divided by 0.152, which is approximately 6.579.
This means that on average, it is expected to take approximately 6.579 games to win on the slot machine. However, it's important to note that this is an average value and individual experiences may vary. Some players may win on their first few games, while others may take more games to win. Nonetheless, on average, it is expected to take approximately 6.579 games to achieve a win.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
A bird is attempting to fly northeast at a constant speed, but a wind blowing southward at 5 miles per
hour blows the bird off course. If the bird’s overall movement (incorporating its intended movement
and the movement due to wind) is at a speed of √53 miles per hour, how fast would it have been traveling if there was no wind?
Answers
Answer:
The value is \(v_b = 9.89 \ miles /hour\)
Step-by-step explanation:
From the question we are told that
The velocity of the wind southward is \(v = 5 j \ miles / hour\)
The resultant velocity of the bird with the with wind is \(V= \sqrt{53}\)
Generally for an object moving in the northwest direction the angle with the horizontal is 45°
Generally the velocity of the bird in the along the x -axis is
\(V_x= v_b cos 45^o i\)
Generally the velocity of the bird in the along the y -axis is
\( V_y=(v_b sin 45^o - 5)j\)
Here \(v_b\) is the velocity of the bird without the wind
Generally the resultant velocity of the bird with the with wind is mathematically represented as
\(V = \sqrt{V_x^2 + V_y^2 }\)
=> \( \sqrt{53} = \sqrt{(v_b cos 45^o)^2 + (v_b sin 45^o - 5)^2 }\)
Generally
\(sin 45^o = \frac{1}{\sqrt{2} }\)
and
\(cos 45^o = \frac{1}{\sqrt{2} }\)
So
\( \sqrt{53} = \sqrt{(v_b* (\frac{1}{\sqrt{2} ))^2 + ([v_b * (\frac{1}{\sqrt{2} ) ]- 5)^2 }\)
=> \(53 = \frac{1}{2} v_b^2 + \frac{1}{2} v_b^2 + 5^2 -2*5 * \frac{1}{\sqrt{2} } v_b\)
=> \( 53 = v_b^2 + 25 - 5 \sqrt{2} v_b\)
=> \( v_b^2 - 5 \sqrt{2} v_b -28 = 0\)
Solving the above quadratic equation using quadratic formula we obtain that
\(v_b = 9.89 \ miles /hour\)
The other value is negative so we do not make use of it because we know that the bird is moving in the positive x and y axis
teacher didnt explain anything just gave the work.

Answers
Answer:
The y-int is -2. The slope is -3/5.
Step-by-step explanation:
Answer:
The 3rd and 4th boxes should be checked. (y-int. is -2, and the slope is -3/5)
Step-by-step explanation:
This is because it is in the form y=mx + b, where b is the y-intercept and m is the slope.
In a standard deck of cards what is the probability of choosing a red king replacing it and then choosing and then a club.
Answers
Answer:
1/104
Step-by-step explanation:
The probability of choosing a red king is 2/52 since there are only two red kings in a deck of 52 cards...the probability of choosing a club would be 13/52 since there are 13 club cardsin a deck of 52 cards
Therefore the probability of choosing both by replacing the king would be 2/52 × 13/52 giving us 1/104
2.AsquareHipushas an area of 64 square inches. It is enlarged by a scale factorof Ž. What is the length of one side of the new square?Step One Find the lengths of the sides of the original square, givennengths-es notits area.weenrThe area is 64. If the sides are n, then n xn= 64 and n="DeanStep Two Multiply the length by the scale factor.8 Xسا |M=The length of the new square is 12 inches.

Answers
We must find the length of one side of the new square.
Step one
The area of the square is 64. We know that the is of a rectangle is given by n x n, so:
\(n\times n=64.\)The value of n is a number that multiplied by itself gives us 64, that number is 8, so we have:
\(n=8.\)Step two
The length of one side of the new square is obtained by multiplying the original length 8 by the scale factor 3/2, which gives us:
\(8\times\frac{3}{2}=\frac{8\times3}{2}=\frac{24}{2}=12.\)Answer
\(\begin{gathered} n=8, \\ 8\times\frac{3}{2}=12. \end{gathered}\)There are 10 Superscript 9 bytes in a gigabyte. There are 10 Superscript 6 bytes in a megabyte. How many times greater is the storage capacity of a 1-gigabyte flash drive than a 1-megabyte flash drive?
Answers
Answer:
1000 times greater.
Step-by-step explanation:
10^9 / 10*6
= 10^(9-6)
= 10^3
= 1000.
Answer:
just took the test answer is C
Step-by-step explanation:
the difference in the measure of two complementary angle is 28 degrees. find the measure of these angles.please answer this question.
Answers
Answer:
Hey
Step-by-step explanation:
Answer:
9
Step-by-step explanation:
because i said so
X – 3 = 7 so X = thank
Answers
Answer:
x=10
Step-by-step explanation:
x-3(+3)=7+3
We need to add 3 to both sides to isolate x.
x=10
Answer:
x = 10Step-by-step explanation:
x - 3 = 7
x = 7 + 3
x = 10
Rewrite in simplest terms: -8(10r + 10r - 6) - 3r
HELP ME
Answers
After simplifying the expression - 8 ( 10 r + 10 r - 6 ) - 3 r, we get the result as 48 - 163 r.
We are provided with an expression:
- 8 ( 10 r + 10 r - 6 ) - 3 r
We need to write the given expression in the simplest terms that is we need to simplify the expression.
So, we will use the property of BODMAS here.
Solving the bracket first , the expression will become:
= - 8 ( 10 r + 10 r - 6 ) - 3 r
= -8 ( 20 r - 6 ) - 3 r
Now, opening the bracket, we get that:
= - 160 r + 48 - 3 r
Now, combining the like terms, we get the result as:
= - 163 r + 48
= 48 - 163 r
Therefore, after simplifying the expression - 8 ( 10 r + 10 r - 6 ) - 3 r, we get the result as 48 - 163 r.
Learn more about expression here:
https://brainly.com/question/723406
#SPJ9
Kyle is renovating the first floor of his home. He bought 650 square feet of carpet flooring and 800 square feet of vinyl flooring and paid $3,214. He went back to the store and bought an additional 190 square feet of carpet flooring and 80 square feet of vinyl and paid $556.40. Find the cost per square foot
of each type of flooring.
Define the variables
x =
y=
Linear System -
(there should be two, for both x and y
Answers
Step-by-step explanation:
we can define the variables as follows:
x = cost per square foot of carpet flooring
y = cost per square foot of vinyl flooring
Then, we can write two equations to represent the total cost of the first purchase and the total cost of the second purchase:
650x + 800y = 3214 (the total cost of the first purchase)
190x + 80y = 556.40 (the total cost of the second purchase)
This gives us a system of linear equations that we can solve simultaneously to find the cost per square foot of each type of flooring
In a class of students, the following data table summarizes how many students passed
a test and complete the homework due the day of the test. What is the probability that
a student chosen randomly from the class passed the test?
Completed the homework
Did not complete the homework
Passed the test Failed the test
12
2
4
3
Answers
Answer:
20/27
Step-by-step explanation:
The length of a rectangle is increasing at a rate of 7 cm/s and its width is increasing at a rate of 3 cm/s. When the length is 11 cm and the width is 5 cm, how fast is the area of the rectangle increasing?
Answers
Answer: 89 cm^2/minute
Step-by-step explanation:
Initial Area: 11 x 5 = 55 cm^2
Area after 1 minute: 18 x 8 = 144 cm^2
The area of the triangle is increasing by
Four fifths times five times two ninths
Answers
Answer:\(\frac{8}{9}\)
Step-by-step explanation:
Four fifths=4/5
two ninths=2/9
\(\frac{4}{5} *5*\frac{2}{9}=\frac{8}{9}\)
Assuming you meant ( four fifths ) * 5 * ( two ninths ), the answer would be 0.88888888888.
If you meant 4/5 x 5 and then x 2/9, the answer would be 8/9, because 4/5 x 5 is 4, and 4 x 2/9 is 8/9.
$9,000 is invested in an account earning 8% interest (APR), compounded daily.
Write a function showing the value of the account after t years, where the annual
growth rate can be found from a constant in the function. Round all coefficients in
the function to four decimal places. Also, determine the percentage of growth per
year (APY), to the nearest hundredth of a percent.

Answers
Answer:
The formula for calculating the value of an account with compound interest is:
A = P(1 + r/n)^(nt)
where:
A = the final amount
P = the principal (starting amount)
r = the annual interest rate (as a decimal)
n = the number of times the interest is compounded per year
t = the time period in years
For this problem, we have:
P = $9,000
r = 8% = 0.08 (APR)
n = 365 (compounded daily)
t = number of years
So the function for the value of the account after t years is:
f(t) = 9000(1 + 0.08/365)^(365t)
Simplifying and rounding to four decimal places:
f(t) = 9000(1.000219178)^t
f(t) = 9000(1.0002)^t
To determine the annual percentage yield (APY), we can use the formula:
APY = (1 + r/n)^n - 1
where r = 0.08 (APR) and n = 365 (compounded daily)
APY = (1 + 0.08/365)^365 - 1
APY = 0.0833 or 8.33%
So the account is growing at an annual rate of 8.33%.
3. What is the vertex of the graph of the
function f(x) = x2 + 8x?
A (-4, 16) B (0,8)
C(-4, -16) D(0, -8)
-
Answers
Answer:
A
Step-by-step explanation:
Given a parabola in standard form
f(x) = ax² + bx + c ( a ≠ 0 )
then the x- coordinate of the vertex is
x = - \(\frac{b}{2a}\)
f(x) = x² + 8x ← is in standard form
with a = 1 , b = 8 , then
x = - \(\frac{8}{2}\) = - 4
substitute x = - 4 into f(x) for corresponding y- coordinate
f(- 4) = (- 4)² + 8(- 4) = 16 - 32 = - 16
vertex = (- 4, - 16 ) → A