A 6pint bucket of paint costs $28.44 what is the price per cup
Answers
Answer:
I think there answer is 4.74
Step-by-step explanation:
so you divide
\(6 \div 28.44 \: and \: you \: get \: answer\)
Related Questions
A healthy school lunch that is $0.75 more than the current lunch has a higher economic
Answers
The fact that the healthy school lunch has a higher price than the current lunch means that it has a higher economic cost.
What is an economic cost?An economic cost in this scenario, is the increased cost that comes with a commodity having greater perceived value.
A healthy school lunch will help a person stay healthy which is why it has more value than the current lunch. This is the reason for its higher price.
Find out more on economic cost at https://brainly.com/question/902188.
#SPJ1
Answer: cost
Step-by-step explanation:
which polynomial correctly combines the like terms and expresses the given polynomial in standard form? 9xy³ -4y⁴ -10x²y² + x³y + 3x⁴ + 2x²y² - 9y⁴
Answers
Answer:
3x^4+(x^3)y-8x^2y^2+9xy^3-13y^4
Step-by-step explanation:
3x^4+(nothing)=3x^4
x^3y+(nothing)=x^3y
-10x^2y^2=2x^2y^2=-8x^2y^2
9xy^3+(nothing)=0
-4y^4-9y^4=-13y^4
Add it all up and write the terms by descending order of exponent value, and u get my answer.
Find the value of perimeter of ABCD. Assume that segments that appear to be tangent are tangent

Answers
The final statement is: The perimeter of the quadrilateral is given by 71 units.
What is Perimeter?The perimeter of a shape is defined as the total distance around the shape. It is the length of the outline or boundary of any two-dimensional geometric shape
Given here: A quadrilateral ABCD with a circle inscribed in it.
Now sides of the quadrilateral form tangents from a common point (vertex)
Thus they must be equal
∴ Perimeter of the ABCD is = 29+12+2.5+2.5+21-17+21
= 71 units
Hence, The perimeter of the quadrilateral is given by 71 units.
Learn more about perimeter here:
https://brainly.com/question/20693059
#SPJ1
What is the area of this figure? 28 km 18 km 9 km 7 km 19 km 25 km
Answers
Answer:
2,154,600
Step-by-step explanation:
find the area of the shaded region (round to four decimal places) the graph depicts the standard normal distribution of bone density scores with the mean of 0 and the standard deviation of 1

Answers
The area of the shaded region equals
\(P(-0.96Graphically you can see it like thisSo, you have:
The values are obtained from the table "Standard Normal Distribution"
\(\begin{gathered} P(-0.96Therefore, the area of the shaded region is 0.7277.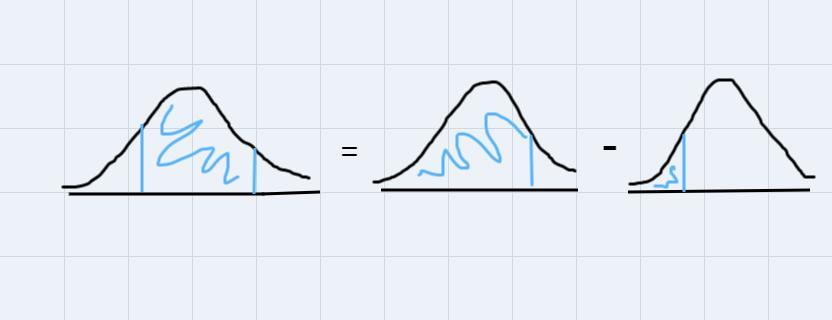
Helppp please!!!!!!

Answers
What is the relative maximum point for the function shown on the graph?
A)(0, -1)
B)(-3,0)
C(-2,-5)
D)(2,5)
Helpppp plzzz

Answers
Answer:
A) (0, -1)
Step-by-step explanation:
A relative maximum point is a point where the function changes direction from increasing to decreasing (making that point a "peak" in the graph)
(0, -1)
Sam weighed 105 lbs. before the holidays. She now weighs 110 lbs. Find the Percent of Change.
Answers
Answer:
5%
Step-by-step explanation:
105=100
110=x
*cross multiply*
=100x110/105
=104.76
=100-105
=5%
subtract the answer gotten with the 100 %
what is the constant of proportionality in y=3 and x=46.50
plsssssssss help its for homework
Answers
Answer:
58y is the correct answer to this question
Show why (2×3×7)^4 = 2^4 × 3^4 × 7^4 show work
Answers
\( {a}^{m} \times {b}^{m} = ( {ab)}^{m} \)
(2×3×7)⁴=(2×3)⁴×7⁴(2×3×7)⁴=(2×3×7)⁴RHS=LHSplease mark this answer as brainlist
Since she bought it. Nissa's favorite baseball card increased in value from $1.20 to $6.
What is the percent change in the card's value?
Enter your answer in the box

Answers
Answer:
500%
Step-by-step explanation:
\( \frac{6 \times 100}{1.2} = 500\%\)
Last year, Bob had $10,000 to invest. He invested some of it in an account that paid 10% simple interest per year, and he invested the rest in an account that paid 8% simple interest per year. After one year, he received a total of $820 in interest. How much did he invest in each account?
Answers
Given:
The total amount is P = $10,000.
The rate of interest is r(1) = 10% 0.10.
The other rate of interest is r(2) = 8%=0.08.
The number of years for both accounts is n = 1 year.
The total interest earned is A = $820.
The objective is to find the amount invested in each account.
Explanation:
Consider the amount invested for r(1) as P(1), and the interest earned as A(1).
The equation for the amount obtained for r(1) can be calculated as,
\(\begin{gathered} A_1=P_1\times n\times r_1 \\ A_1=P_1\times1\times0.1 \\ A_1=0.1P_1\text{ . . . . .(1)} \end{gathered}\)Consider the amount invested for r(2) as P(2), and the interest earned as A(2).
The equation for the amount obtained for r(2) can be calculated as,
\(\begin{gathered} A_2=P_2\times n\times r_2 \\ A_2=P_2\times1\times0.08 \\ A_2=0.08P_2\text{ . . . . . (2)} \end{gathered}\)Since, it is given that the total interest earned is A=$820. Then, it can be represented as,
\(A=A_1+A_2\text{ . . . . . (3)}\)On plugging the obtained values in equation (3),
\(820=0.1P_1+0.08P_2\text{ . . . . .(4)}\)Also, it is given that the total amount is P = $10,000. Then, it can be represented as,
\(\begin{gathered} P=P_1+P_2 \\ 10000=P_1+P_2 \\ P_1=10000-P_2\text{ . }\ldots\ldots.\text{. .(3)} \end{gathered}\)Substitute the equation (3) in equation (4).
\(undefined\)Can anyone help please. I got C but I don’t know.

Answers
explain how to determine whether or not 11/12 is the correct answer to the problem 1 1/4 - 1 / 3
Answers
Answer:
11/12 is correct
Explanation:
To find the result of 1 1/4 - 1/3, we need to write the first number as a fraction, so:
\(1\frac{1}{4}=\frac{(1\times4)+1}{4}=\frac{4+1}{4}=\frac{5}{4}\)Then, 1 1/4 - 1/3 is equivalent to 5/4 - 1/3, so the correct answer is:
\(\frac{5}{4}-\frac{1}{3}=\frac{5(3)-4(1)}{4(3)}=\frac{15-4}{12}=\frac{11}{12}\)Therefore, 11/12 is the correct answer to the problem
a normal distribution with a mean of 25 minutes with a population standard deviation of 5 minutes. The store manager sampled 100 customers and found that the mean waiting time was 24.25 minutes. At the 0.01 significance level, test if the mean waiting time is less than 25 minutes.
Answers
Answer:
\(z=\frac{24.25-25}{\frac{5}{\sqrt{100}}}=-1.5\)
The p value for this case would be given with this probability:
\(p_v =P(z<-1.5)=0.0668\)
For this case since the p value is higher than the significance level of 0.01 we have enough evidence to fail to reject the null hypothesis and we don't have enough evidence to conclude that the true mean is significantly less than 25 min.
Step-by-step explanation:
Information given
\(\bar X=242.5\) represent the sample mean
\(\sigma=5\) represent the population deviation
\(n=100\) sample size
\(\mu_o =25\) represent the value to check
\(\alpha=0.01\) represent the significance level
z would represent the statistic
\(p_v\) represent the p value
Hypotheis to test
We want to verify if the true mean is less than 25 min, the system of hypothesis would be:
Null hypothesis:\(\mu \geq 25\)
Alternative hypothesis:\(\mu < 25\)
The statistic would be given by:
\(z=\frac{\bar X-\mu_o}{\frac{\sigma}{\sqrt{n}}}\) (1)
And replacing the info given we got:
\(z=\frac{24.25-25}{\frac{5}{\sqrt{100}}}=-1.5\)
The p value for this case would be given with this probability:
\(p_v =P(z<-1.5)=0.0668\)
For this case since the p value is higher than the significance level of 0.01 we have enough evidence to fail to reject the null hypothesis and we don't have enough evidence to conclude that the true mean is significantly less than 25 min.
How much will you need to invest at 3% to have earned $900 in interest in 4 years?
Answers
Answer:
You will have earned $113 in interest.
Step-by-step explanation:
After investing for 4 years at 3% interest, your initial investment of $900 will have grown to $1,013.
To find the amount you need to invest, we can use the formula for simple interest:
\(\displaystyle\sf \text{{Interest}} = \text{{Principal}} \times \text{{Rate}} \times \text{{Time}}\)
Here, the principal is the amount you need to invest, the rate is 3% (or 0.03 as a decimal), and the time is 4 years. We can rearrange the formula to solve for the principal:
\(\displaystyle\sf \text{{Principal}} = \frac{{\text{{Interest}}}}{{\text{{Rate}} \times \text{{Time}}}}\)
Plugging in the given values, we get:
\(\displaystyle\sf \text{{Principal}} = \frac{{900}}{{0.03 \times 4}}\)
Simplifying further:
\(\displaystyle\sf \text{{Principal}} = \frac{{900}}{{0.12}}\)
Calculating the division:
\(\displaystyle\sf \text{{Principal}} = 7500\)
Therefore, you will need to invest $7500 at 3% to have earned $900 in interest in 4 years.
pls answer this question, I don't understand it.

Answers
The two numbers could be 0.43× 10⁻⁵ and, 0.06× 10⁻³.
Here, we have,
given that,
the product of two number in scientific notation is: 0.0258 × 10⁻⁸
now, let the two numbers be:
0.43× 10⁻⁵ and, 0.06× 10⁻³
we get,
0.43× 10⁻⁵ × 0.06× 10⁻³
= 0.43 × 0.06× 10⁻⁵ × 10⁻³
= 0.43 × 0.06 × 10⁻⁵⁻³
=0.43 × 0.06× 10⁻⁸
=0.0258 × 10⁻⁸
Hence, The two numbers could be 0.43× 10⁻⁵ and, 0.06× 10⁻³.
To learn more on multiplication click:
brainly.com/question/5992872
#SPJ1
NO LINKS!! Please help me with this statement Part 2mm

Answers
Answer:
y = 2x² + 8x - 5--------------------------------------
Vertex form of a quadratic function:
y = a(x - h)² + k, where (h, k) is vertex and a - constantGiven (h, k) = (-2, -13) and a point (0, - 5).
Substitute all into equation and solve for a:
-5 = a(0 - (-2))² - 13-5 = 4a - 134a = 13 - 54a = 8a = 2The parabola is:
y = 2(x + 2)² - 13Convert it to the standard form:
y = 2(x + 2)² - 13y = 2(x² + 4x + 4) - 13y = 2x² + 8x + 8 - 13y = 2x² + 8x - 5Answer:
\(f(x)=2x^2+8x-5\)
Step-by-step explanation:
\(\boxed{\begin{minipage}{5.6 cm}\underline{Vertex form of a quadratic equation}\\\\$y=a(x-h)^2+k$\\\\where:\\ \phantom{ww}$\bullet$ $(h,k)$ is the vertex. \\ \phantom{ww}$\bullet$ $a$ is some constant.\\\end{minipage}}\)
Given:
Vertex = (-2, -13)Point = (0, -5)Substitute the given vertex and point into the Vertex formula and solve for a:
\(\implies -5=a(0-(-2))^2+(-13)\)
\(\implies -5=a(0+2)^2-13\)
\(\implies -5=4a-13\)
\(\implies 4a=8\)
\(\implies a=2\)
Substitute the given vertex and found value of a into the Vertex formula:
\(y=2(x+2)^2-13\)
The standard form of a quadratic function is f(x) = ax² + bx + c
Expand the function in vertex form to standard form:
\(\implies y=2(x^2+4x+4)-13\)
\(\implies y=2x^2+8x+8-13\)
\(\implies y=2x^2+8x-5\)
What is the solution to the compound inequality: 10<2x-4<20
Answers
Answer:
7 < x < 12
Step-by-step explanation:
To solve this inequality, solve it the same way you do a normal function. Perform the same actions on both sides of the inequality.
\(10 < 2x-4 < 20\\14 < 2x < 24\\7 < x < 12\)
anyone that knows about cos, tan, and csc please help!
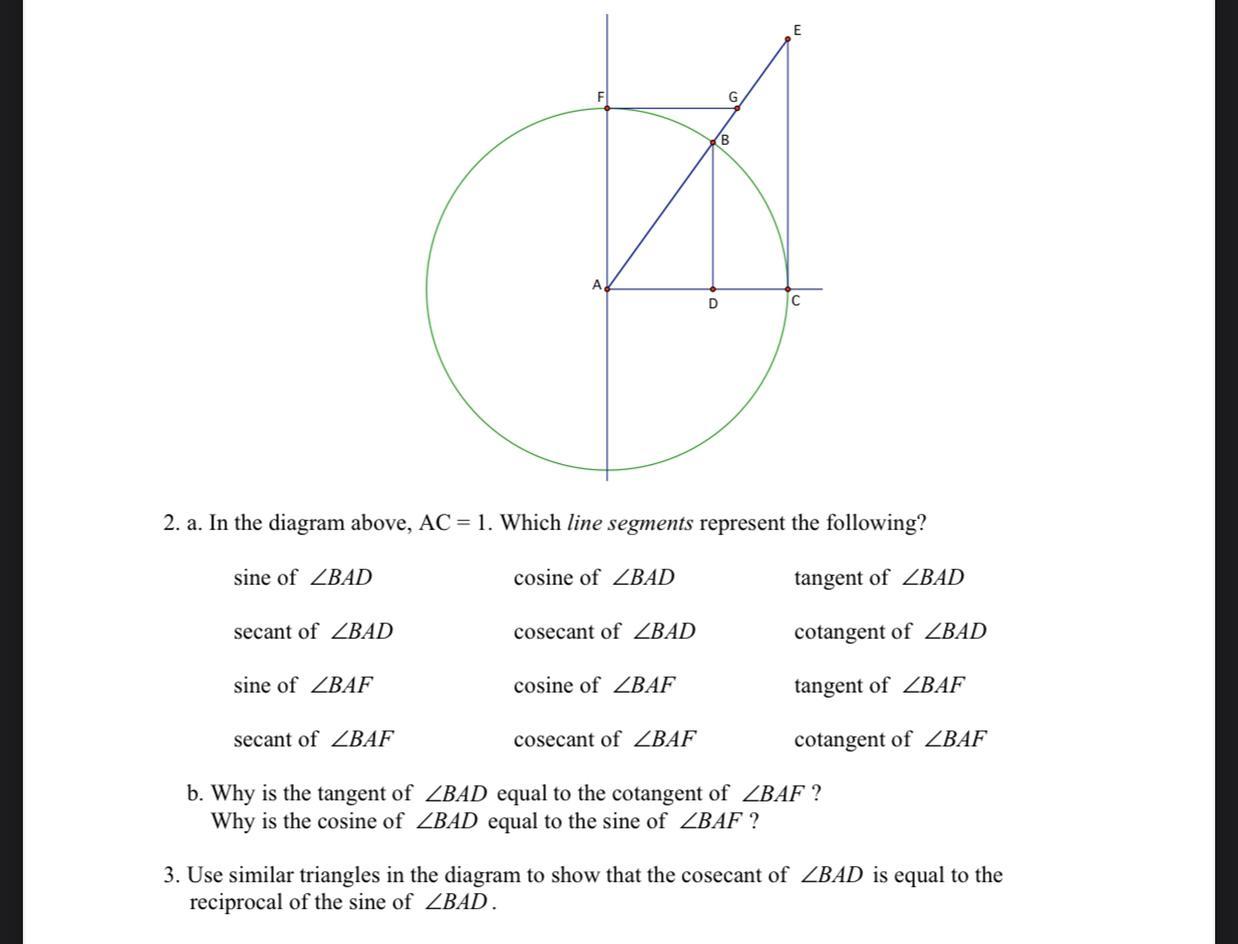
Answers
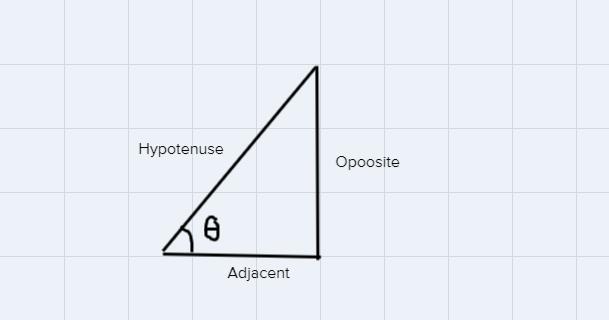
Can someone help me with number 1 and 2

Answers
The first one is 2 hundredths and the second one is 800+60+3. 01 + 004 +0001
Consider the function y= f(x) shown below. Which of the following statements is true?

Answers
Answer: d) none of these
Step-by-step explanation:
\(a)\quad \displaystyle \lim_{x \to 1} f(x)=\large\boxed{1} \\\\\\b)\quad f(1)=\large\boxed{3}\\\\\\c) \displaystyle \lim_{x \to 1} f(1) \neq f(1) \quad \text{therefore it is not continuous}\\\\\\d) \displaystyle \lim_{x \to 1} f(1) = 1,\quad f(1)=3\quad \longrightarrow \quad \displaystyle \lim_{x \to 1} f(1) \neq f(1)\)
In a statewide lottery, one can buy a ticket for $1. With probability .0000001, one wins a million dollars ($1,000,000), and with probability .9999999 one wins nothing ($0). Let Y denote the winnings from buying one ticket. Construct the probability distribution for Y. Show that the mean of the distribution equals .10, corresponding to an expected return of 10 cents for the dollar paid.
Answers
Using the expected value, it is found that the mean of the distribution equals $0.1.
The expected value, which is the mean of the distribution, is given by each outcome multiplied by it's probability.
The probabilities of each outcome are:
.0000001 probability of earning $1,000,000..9999999 probability of earning $0.Thus, the mean is given by:
\(E(Y) = 0.0000001(1000000) + 0.9999999(0) = 0.1\)
Thus showing that the expected value is $0.1.
A similar problem is given at https://brainly.com/question/24855677
Determine the equation of the circle with center (-7, -4) containing the point
(-1,-8).
Answers
Answer:
(-1, -8) is:(x + 7)^2 + (y + 4)^2 = 52
Step-by-step explanation:
i literally just learned this today so here we go:
The equation of a circle with center (h, k) and radius r is given by:
(x - h)^2 + (y - k)^2 = r^2
We are given the center of the circle as (-7, -4), so we can substitute these values for h and k:
(x - (-7))^2 + (y - (-4))^2 = r^2
(x + 7)^2 + (y + 4)^2 = r^2
We also know that the circle contains the point (-1, -8).
We can substitute these values for x and y, and solve for r:
(-1 + 7)^2 + (-8 + 4)^2 = r^2
36 + 16 = r^2
r^2 = 52
Substituting this value of r^2 into the equation for the circle, we get:
(x + 7)^2 + (y + 4)^2 = 52
Therefore, the equation of the circle with center (-7, -4) containing the point (-1, -8) is:(x + 7)^2 + (y + 4)^2 = 52
Give the system of inequalities x-2y=15. 2x+4y=-18 what are x and y
Answers
Answer:
For x-2y=15, it's x= 15 + 2y. For 2x+4y=-18, it's x= -9-2y.
Step-by-step explanation:
Divide 1235 by 25.Write the remainder as fraction.
Answers
is (3 + 5) + 4 = 3 + (5 + 4) a Multiplicative Identity
Answers
If an object with mass m is dropped from rest, one model for its speed v after t seconds, taking air resistance into account, is given by the following where g is the acceleration due to gravity and c is a positive constant describing air resistance.
v=((mg)/c) \(1-e^(-(ct)\/m)\)
(a) Calculate the following.
lim_(t->infinity) v= __________
What is the meaning of this limit?
1)It is the time it takes the object to reach its maximum speed.
2)It is the speed the object approaches as time goes on.
3)It is the time it takes for the object to stop.
4)It is the speed the object reaches before it starts to slow down.
(b) For fixed t, use l'Hospital's Rule to calculate the following.
lim_(c->0**+) v= ___________
What can you conclude about the velocity of a falling object in a vacuum?
1)The speed has nothing to do with the elapsed time. The heavier the object is the faster it will fall.
2)The speed is jointly proportional to the time and the mass. The longer the object falls and the heavier it is the faster it will fall.
3)The speed is proportional to the elapsed time. It doesn't depend on the mass. The longer the object falls the faster it will fall.
Answers
The speed is proportional to the elapsed time. It doesn't depend on the mass. a)Mg/c is the limit and b)gt is the limit
What is speed?
Speed is defined as the rate of change of distance with time. It has the dimension of distance by time. Thus, the SI unit of speed is given as the combination of the basic unit of distance and the basic unit of Timea) lim t-->∞ v = mg/c
mg/c is the limit
2)It is the speed the object approaches as time goes on.
b) lim c-->0^(+) v = gt.
gt is the limit
3)The speed is proportional to the elapsed time. It doesn't depend on the mass. The longer the object falls the faster it will fall because same acceleration g it will not depend on mass.
To learn more about proportion check the given link
https://brainly.com/question/19994681
#SPJ4
suppose a population consists of 5000 being surveyed could result in sample statistic but not parameter
Answers
Use the properties of exponents to simplify the expression:

Answers
The simplified expression for \($(27^{\frac{1}{2} }) ^{\frac{2}{3} }\) is equal to 3.
How can you simplify → aˣ/aⁿ?We can write the simplified form of the given expression using the exponent rule as -
{aˣ/aⁿ} = {aˣ a⁻ⁿ} = {aˣ ⁻ ⁿ}
Given is the expression as -
\($(27^{\frac{1}{2} }) ^{\frac{2}{3} }\)
We can simplify the expression as -
\($(27^{\frac{1}{2} }) ^{\frac{2}{3} } = (27)^{\frac{1}{2} \times \frac{2}{3} }\)
\($(27^{\frac{1}{2} }) ^{\frac{2}{3} } = 27^{\frac{1}{3} }\)
\($(27^{\frac{1}{2} }) ^{\frac{2}{3} } = (3)^{3}^{\frac{1}{3} }\)
\($(27^{\frac{1}{2} }) ^{\frac{2}{3} } = 3\)
Therefore, the simplified expression for \($(27^{\frac{1}{2} }) ^{\frac{2}{3} }\) is equal to 3.
To solve more questions on exponents, visit the link below -
brainly.com/question/12431044
#SPJ1