A 12 ounce Pepsi costs $1.44. A 16 ounce Pepsi costs $2.24. Which is the better buy?
The answer choices are:
A. 12 ounce; $0.15 per ounce.
B. 16 ounce; $0.14 per ounce.
C. 12 ounce; $0.12 per ounce.
D. 16 ounce; $0.09 per ounce.
Answers
$1.44/12 oz x/1 oz x=$.12
$2.24/16oz x/1 oz x=$.14
Related Questions
In ΔMNO, \overline{MO}
MO
is extended through point O to point P, \text{m}\angle MNO = (3x+11)^{\circ}m∠MNO=(3x+11)
∘
, \text{m}\angle OMN = (2x+20)^{\circ}m∠OMN=(2x+20)
∘
, and \text{m}\angle NOP = (8x-5)^{\circ}m∠NOP=(8x−5)
∘
. What is the value of x?x?
Answers
Answer:
x = 12Step-by-step explanation:
Given the triangle MNO which is extended through point O to point P, we are given the followings;
Interior angles;
∠MNO=(3x+11)
∠OMN=(2x+20)
Exterior angle;
∠NOP=(8x−5)
To find x, we will use the theorem, "The sum of the interior angles is equal to the exterior"
Hence;
3x+11+2x+20 = 8x - 5
5x + 31 = 8x - 5
Collect like terms;
5x - 8x = -5-31
-3x = -36
x = -36/-3
x = 12
Hence the value of x is 12
Answer: x=12
Step-by-step explanation:
Which of the following statements for a simple graph is correct?a) Every path is a trailb) Every trail is a pathc) Every trail is a path as well as every path is a traild) Path and trail have no relation
Answers
Statement (c) is correct for a simple graph. Every trail is a path, and every path is a trail.
In graph theory, a simple graph is an undirected graph with no loops or multiple edges between the same pair of vertices. A path in a graph is a sequence of vertices where each consecutive pair is connected by an edge. A trail in a graph is a path that allows for repeated vertices and edges.
Statement (a) is not correct because not every path is a trail. A path does not allow for repeated vertices or edges, whereas a trail does.
Statement (b) is not correct because not every trail is necessarily a path. A trail may contain repeated vertices or edges, but a path does not.
Statement (d) is not correct because paths and trails do have a relation. A trail is a more general concept that encompasses paths by allowing for repetition of vertices and edges.
Therefore, statement (c) is the correct statement. In a simple graph, every trail is a path, and every path is a trail.
Learn more about vertices here : https://brainly.com/question/29154919
#SPJ11
2s 5s + 3t Let W be the set of all vectors of the form B Show that W is a subspace of R4 by finding vectors u and v such that W = Span{u,v}. 4s - 5t 2t Write the vectors in W as column vectors. 2s 5s + 3t EM = su + tv 45-50 2t What does this imply about W? O A. W=s+t OB. W=U + V OC. W = Span{u, v} OD. W = Span{s,t} Explain how this result shows that W is a subspace of R4. Choose the correct answer below. O A. Since s and t are in R and W = u + v, W is a subspace of R4. B. Since s and t are in R and W = Span{u,v}, W is a subspace of R4. OC. Since u and v are in R4 and W = Span{u,v}, W is a subspace of R4. D. Since u and v are in R4 and W = u + V, W is a subspace of R4.
Answers
Since W satisfies all three conditions, it is a subspace of R4. And since we have shown that W = Span{u, v}, we can choose answer (C): "Since u and v are in R4 and W = Span{u, v}, W is a subspace of R4."
What is sub space?
In mathematics, a subspace is a subset of a vector space that is itself a vector space under the same operations of vector addition and scalar multiplication as the original space.
To show that W is a subspace of R4, we need to show that it satisfies three conditions:
The zero vector is in W.
W is closed under vector addition.
W is closed under scalar multiplication.
First, let's find vectors u and v such that W = Span{u,v}. We are given that a vector B in W has the form:
B = (2s + 5s + 3t, 4s - 5t, 2t, 45-50)
We can rewrite this as:
B = (7s, 4s, 0, 45-50) + (3t, -5t, 2t, 0)
So, we can take u = (7, 4, 0, -5) and v = (3, -5, 2, 0) to span W.
Now, let's check the three conditions:
The zero vector is in W:
Setting s = t = 0 in the expression for B gives us the vector (0, 0, 0, -5). This vector is in W, so the zero vector is in W.
W is closed under vector addition:
Let B1 and B2 be two vectors in W. Then, we have:
B1 = su1 + tv1 = a1u + b1v
B2 = su2 + tv2 = a2u + b2v
where a1, b1, a2, b2 are scalars.
Then, B1 + B2 is given by:
B1 + B2 = su1 + tv1 + su2 + tv2
= (a1u + b1v) + (a2u + b2v)
= (a1 + a2)u + (b1 + b2)v
which is also in W, since it can be expressed as a linear combination of u and v.
W is closed under scalar multiplication:
Let B be a vector in W and let k be a scalar. Then, we have:
B = su + tv = au + bv
where a, b are scalars.
Then, kB is given by:
kB = k(su + tv)
= (ks)u + (kt)v
which is also in W, since it can be expressed as a linear combination of u and v.
Therefore, since W satisfies all three conditions, it is a subspace of R4. And since we have shown that W = Span{u, v}, we can choose answer (C): "Since u and v are in R4 and W = Span{u, v}, W is a subspace of R4."
To learn more about sub spaces from the give link:
https://brainly.com/question/30318872
#SPJ1
help me please!
1/2(-4+6n) = 1/3n + 2/3 (n+9)
Answers
Answer:
n = 4
Step-by-step explanation:
simplify left side first:
(1/2) (-4 + 6n) = -2 + 3n.
now simplify right side:
(1/3)n + (2/3) (n + 9) = (1/3)n + (2/3)n + (2/3) (9) = (3/3)n + 6 = n + 6.
so, we now have -2 + 3n = n + 6.
subtract n from both sides and add 2 to both sides
-2 + 3n - n + 2 = n + 6 - n + 2
2n = 8
n = 4
1
2
(
−
4
+
6
)
=
1
3
+
2
3
(
+
9
)
The answer is n=4
answer please i need help with this

Answers
\(\qquad\qquad\huge\underline{\boxed{\sf Answer}}\)
Let's evaluate ~
\(\qquad \sf \dashrightarrow \: \dfrac{1}{3 {}^{ - 2} \times {x}^{ - 4} \times {y}^{2} } \)
plug in the values :
\(\qquad \sf \dashrightarrow \: \dfrac{1}{3 {}^{ - 2} \times {3}^{ - 4} \times { - 1}^{2} } \)
\(\qquad \sf \dashrightarrow \: \dfrac{1}{3 {}^{ - 6} {}^{ } {}^{} } \)
\(\qquad \sf \dashrightarrow \: {3}^{6} \)
\(\qquad \sf \dashrightarrow \:729\)
Therefore, B is the Correct choice ~
・ .━━━━━━━†━━━━━━━━━.・
Answer:
729
Step-by-step explanation:
Given expression:
\(\sf \dfrac{1}{3^{-2}x^{-4}y^2}\)
Apply exponent rule \(\sf \dfrac{1}{a^{-b}}=a^b\)
\(\sf \implies \dfrac{3^2x^4}{y^2}\)
\(\sf \implies \dfrac{9x^4}{y^2}\)
Substituting x = 3 and y = -1:
\(\sf \implies \dfrac{9(3)^4}{(-1)^2}\)
\(\sf \implies \dfrac{9 \cdot 81}1}\)
\(\sf \implies 729\)
To amend a country's constitution, 5 6 of the 52 states in that country must approve the amendment. If 44 states approve an amendment, will the constitution be amended
Answers
Answer: Yes. It will be amended
Step-by-step explanation:
Since 5/6 of the 52 states in a country must approve the amendment before the country's constitution is amended, then the number of states that must approve it will be:
= 5/6 × 52
= 43.33
= 43 approximately
Since 44 states approve an amendment, the constitution be amended since it's more than 5/6 of the 52 states.
Seven years ago, Mrs Grey decided to invest R18 000 in a bank account that paid simple interest at 4,5% p.a. 4.1.1 Calculate how much interest Mrs Grey has earned over the 7 years. 4.1.2 Mrs Grey wants to buy a television set that costs R27 660,00 now. If the average rate of inflation over the last 5 years was 6,7% p.a., calculate the cost of the television set 5 years ago. 4.1.3 At what rate of simple interest should Mrs Grey have invested her money 7 years ago if she intends buying the television set now using only her original investment of R18 000 and the interest earned over the last 7 years?
Answers
The interest earned by Mrs Grey over the 7 years is R5670. The cost of the television set 5 years ago was R20,600.
4.1.1 To calculate the interest earned by Mrs Grey over 7 years, we use the formula for simple interest: Interest = Principal x Rate x Time. Mrs Grey's principal is R18,000 and the rate is 4.5% per annum. The time is 7 years. Using the formula, we can calculate the interest as follows:
Interest = R18,000 x 0.045 x 7 = R5670. Therefore, Mrs Grey has earned R5670 in interest over the 7 years.
4.1.2 To calculate the cost of the television set 5 years ago, we need to account for the inflation rate. The cost of the television set now is R27,660. The average rate of inflation over the last 5 years is 6.7% per annum. We can use the formula for compound interest to calculate the original cost of the television set:
Cost 5 years ago = Cost now / (1 + Inflation rate)^Time
Cost 5 years ago = R27,660 / (1 + 0.067)^5 = R20,600. Therefore, the cost of the television set 5 years ago was R20,600.
4.1.3 To determine the rate of simple interest Mrs Grey should have invested her money at 7 years ago, we can use the formula for interest: Interest = Principal x Rate x Time. We know the principal is R18,000, the time is 7 years, and the interest earned is R5670. Rearranging the formula, we can solve for the rate:
Rate = Interest / (Principal x Time)
Rate = R5670 / (R18,000 x 7) ≈ 0.0448 or 4.48% per annum. Therefore, Mrs Grey should have invested her money at a rate of approximately 4.48% per annum to have earned enough interest to purchase the television set using only her original investment and the interest earned over the 7 years.
Learn more about simple interest here:
brainly.com/question/30964674
#SPJ11
10-1/2x<-18 which inequality represents the solution to this inequality?
Answers
The solution for inequality 10 - 1/2x < -18 is 0 < x < 1/56.
What is an inequality?
In Algebra, an inequality is a mathematical statement that uses the inequality symbol to illustrate the relationship between two expressions. An inequality symbol has non-equal expressions on both sides. It indicates that the phrase on the left should be bigger or smaller than the expression on the right, or vice versa.
The given inequality is -
10 - 1/2x < -18
Solve the inequality to get the value for x.
First collect all the like terms -
-1/2x < -18 + (-10)
Then use arithmetic operation of addition -
-1/2x < -28
Multiply (-1) to both the sides -
-1/2x × (-1) < -28 × (-1)
1/2x < 28
Then move the coefficient of variable to right hand side of the equation -
x < -1 / (2 × (-28))
Then use arithmetic operation of multiplication and division-
x < 1/56
Therefore, the inequality is 0 < x < 1/56.
To learn more about inequality from the given link
https://brainly.com/question/11234618
#SPJ1
Ryan was traveling by car at an average speed of 40.3 miles per hour.
He will cover 322.4 miles in hours.
Answers
Answer:
your answer is 8
Step-by-step explanation:
If you divide 322.4 by the speed 40.3 you would get 8 the amount of hours traveling the given distance.
If you dont think the answer is correct you can simply mutiply 40.3 by 8 to ensure that 322.4 miles is in fact how far you will go in that time
hope this help. Have a good day!
\
Bye
PLS HELP ASAP!!!! 50 PTS

Answers
Answer: x=4
Step-by-step explanation:
6x + 10 = 5x + 14
x + 10 = 14
x = 4
x+10=14
x=4
Select the correct answer. Let f(x) and g(x) be polynomials as shown below. Which of the following is true about f(x) and g(x)? f(x) and g(x) are closed under multiplication because when multiplied, the result will be a polynomial. f(x) and g(x) are closed under multiplication because when multiplied, the result will not be a polynomial. f(x) and g(x) are not closed under multiplication because when multiplied, the result will be a polynomial. f(x) and g(x) are not closed under multiplication because when multiplied, the result will not be a polynomial.
Answers
f(x) and g(x) are not closed under subtraction because when subtracted, the result will be a polynomial, the correct option is B.
What is Polynomial?A polynomial is a mathematical equation that solely uses the operations addition, subtraction, multiplication, and non-negative integer exponentiation of variables. Variables are sometimes known as indeterminate in mathematics. Majorly used polynomials are binomial and trinomial.
Given f(x) and g(x) two polynomial functions in the standard form of the polynomial,
According to Closure Property, when something is closed, the output will be the same as the input.
The polynomials f(x) and g(x) can be seen in the image.
On subtracting the two polynomials, the output will be a polynomial and so it is closed under subtraction.
Therefore, The reason why f(x) and g(x) are not closed under subtraction is that the outcome of subtraction will be a polynomial, making option B the best choice.
Learn more about Polynomials here:
https://brainly.com/question/11536910
#SPJ1
Complete question:

How many Dollars in 45 Billion won?
Answers
45 billion Korean Won is equal to 45 million US Dollars.
The formula for (USD) is USD = KRW / 1000. To calculate 45 billion won in USD, we must first convert KRW to USD. 45 billion KRW is equal to 45,000,000,000 KRW. Using the formula above, we can calculate the amount of USD:
USD = 45,000,000,000 KRW / 1000
USD = 45,000,000 USD
Therefore, 45 billion won is equal to 45 million US Dollars.
To better understand this conversion, it is important to remember that one US Dollar is equal to 1000 Korean Won. As an example, if you have 10,000 Korean Won, you can convert that to USD by dividing 10,000 by 1000, which equals 10 USD. The same concept applies when converting larger numbers. To convert 45 billion KRW to USD, we must divide 45,000,000,000 by 1000, which equals 45,000,000 USD.
In conclusion, 45 billion Korean Won is equal to 45 million US Dollars.
Learn more about conversion here:
https://brainly.com/question/28770698
#SPJ4
If the system given has parallel lines, what is the answer?
Answers
We need to see the "given system".
Answer:
Since parallel lines never cross, then there can be no intersection; that is, for a system of equations that graphs as parallel lines, there can be no solution. This is called an "inconsistent" system of equations, and it has no solution.
Step-by-step explanation:
What is the smallest positive value of xxx where the displacement of this wave is zero at t=0t=0?
Answers
The smallest positive value x is mathematically given as
\(x= \pi/B\)
What is the smallest positive value of xxx where the displacement of this wave is zero at t=0?Generally, the equation for is mathematically given as
d) for a displacement of the wave at t=0 is 30 sec
\($A \sin (B x-C(0))=0$\)
\(\begin{aligned}-A \sin B x &=0 \\\sin B x &=\sin n \pi \\B x &=m \pi\end{aligned}\)
Therefore, x=(n \pi)/ 8
Since n equals one for the smallest value, the equation that follows provides an answer for the smallest positive value of x that can be found.
\(\begin{aligned}x &=\frac{n \pi}{B} \\&=\frac{(1) \pi}{B} \\x &=\frac{\pi}{B}\end{aligned}\)
In conclusion, the smallest positive value x is
x= \pi/B
Read more about displacement
https://brainly.com/question/11934397
#SPJ4
Complete Question
The complete Question is attached below
What is the smallest positive value of xxx where the displacement of this wave is zero at t=0t=0?
An anthropologist visits an igloo with a circular floor. While there, she measures it and calculates that it has a circumference of 18.84 yards. What is the floor's diameter?
Answers
Answer:
The diameter of the floor is 6 yards
Step-by-step explanation:
Here, we are to calculate the diameter of a circular floor that has a circumference of 18.84 yards
Mathematically,
C = π * D
where C is the circumference
Plugging the values of the circumference , we have ;
18.84 = 22/7 * D
7 * 18.84 = 22D
D = (7* 18.84)/22 = 5.99 which is approximately 6 yards
lan needs to solve 23 = y + 40. What is the step that shows the inverse operation needed to solve this equation. Find the value of y.
Y=
Answers
Answer:
y=17
Step-by-step explanation:
We move all terms to the left:
23-(y+40.)=0
We add all the numbers together, and all the variables
-(y+40)+23=0
We get rid of parentheses
-y-40+23=0
We add all the numbers together, and all the variables
-1y-17=0
We move all terms containing y to the left, all other terms to the right
-y=17
y=17/-1
y=-17
Feri invests some money.
The rate of interest for the first year is 2.5%.
At the end of the second year the overall percentage increase of Feri's investment is 6.6%.
Find the rate of interest for the second year.
Answers
The rate of interest for 2nd year is 4.1%
How to find the interest rate for the second yearFrom the given parameters;
Rate of interest for 1st year = 2.5
As we know the formula for Simple interest is given by
=> I = (PTR)/100
We will use this formula in the following problem
Let 100 be Feri's investment
At the Rate of interest of 2.5
Interest on 100 = [(100(1)(2.5)]/100 = 2.5
Total amount at end of 1st year = 100 + 2.5 = 102.5
Let x be the rate of interest for 2nd year
At the rate of interest of x
interest on 100 = [(100(1)(x)]/100 = x
Total amount at end of 2st year = 102.5 + x
Given that, at end of the 2 years, the rate of interest becomes 6.6%
Interest on 100 at the rate of 6.6%
=> [(100(1)(6.6)]/100 = 6.6
=> total amount = 100 + 6.6 = 106.6
As we know in both cases, the amount must be equal
=> 102.5 + x = 106.6
=> x = 4.1
Therefore, The rate of interest for 2nd year = 4.1
Learn more about interest rate at: https://brainly.com/question/2294792
#SPJ1
Find the product of (4x + 3y)2
Answers
Answer:
8x+6y
Step-by-step explanation:
multiplyy!!
Guys pls help me!!!!!!

Answers
Answer: count them up on each side
Step-by-step explanation:
Answer:
mmhhh
Step-by-step explanation:
(-9,8) look where it ends
In a direct variation, y=8 when x=2. Write a direct variation equation that shows the relationship between x and y.
Answers
Answer:
y=4x
Step-by-step explanation:
Direct Variation means y=kx where k is a Constant
since y=8 when x=2
y=kx --> 8=k*2 then k=4
Then y=4x
A hand of 12 cards is dealt from a well-shuffled standard 52-card deck of cards. What is the probability that the hand contains 2 Jacks?
a) 0.240156
b) 0.210156
c) 0.190156
d) 0.220156
e) 0.200156
Answers
Therefore, the probability of getting 2 Jacks in a hand of 12 cards is 0.190156, rounded to 6 decimal places.
What is probability?Probability is a measure of the likelihood of an event occurring, expressed as a number between 0 and 1. Events that are certain to happen have a probability of 1, while events that are impossible have a probability of 0. Events that are more likely to happen have a higher probability value, while events that are less likely to happen have a lower probability value. The calculation of probability involves determining the number of ways an event can happen and dividing that by the total number of possible outcomes.
Here,
o find the probability of getting 2 Jacks in a hand of 12 cards from a standard 52-card deck, we can use the hypergeometric distribution.
The total number of ways to choose 12 cards from a deck of 52 is:
C(52, 12) = 52! / (12! * 40!)
= 5,311,735,669
The number of ways to choose 2 Jacks from 4 Jacks is:
C(4, 2) = 4! / (2! * 2!)
= 6
The number of ways to choose 10 non-Jack cards from 48 non-Jack cards is:
C(48, 10) = 48! / (10! * 38!)
= 17,296,959
So the total number of ways to get 2 Jacks and 10 non-Jack cards in a hand of 12 cards is:
6 * 17,296,959 = 103,781,754
Therefore, the probability of getting 2 Jacks in a hand of 12 cards is:
103,781,754 / 5,311,735,669 = 0.0195156
To know more about probability,
https://brainly.com/question/30034780
#SPJ1
please help fast it is due
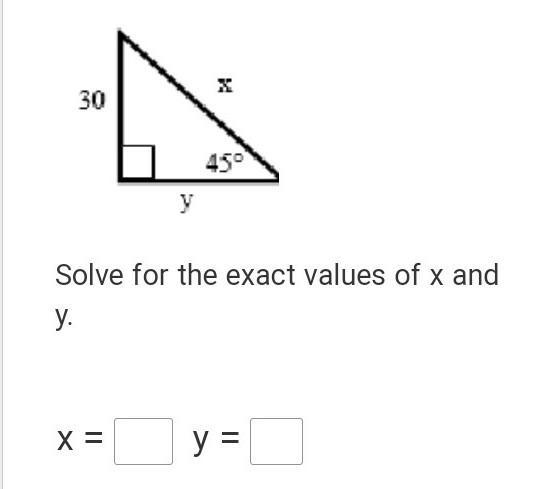
Answers
A right triangle with a 45 degree angle means the two short sides are the same, so y = 30
the hypotenuse is the length of the side x sqrt (2), so x =30sqrt(2)
answer: x = 30sqrt(2) and y = 30
A shipping container will be used to transport several 150-kilogram crates across the country by rail. The greatest weight that can bee loaded into the container is 26000 kilograms. Other shipments weighing 11300 kilograms have already been loaded into the container. Write an inequality representing c, the total number of 150-kilogram crates that can be loaded into the shipping container
Answers
An inequality representing c, the total number of 150-kilogram crates that can be loaded into the shipping container: c ≤ 98
We know that an inequality is a mathematical statement that represents the inequalities between two algebraic expressions with two variables .
It is an unequal relation between two algebraic expressions.
Here, the greatest weight that can be loaded into the container = 26,000 kilograms
the weight of each crate = 150 kilogram
and the weight of other shipment = 11300 kilograms
Let c be the total number of 150-kilogram crates that can be loaded.
So, we get an inequality:
150 c + 11300 ≤ 26,000
150 c ≤ 26,000 - 11300
150 c ≤ 14700
c ≤ 98
Learn more about an inequality here:
brainly.com/question/28816565
#SPJ4
Consider the following language L in the binary alphabet {0, 1}: L = {w = bob1...bn : [ 2n-ib;]3 = 1; n >0} O 0}. O
Answers
L is the collection of all binary strings that contain the character "bob" and satisfy the requirement that the residue of 2n-i modulo 3 is 1, where n is the number of characters after the first instance of "bob."
What is the language L = {w = bob1...bn : [2n-i]3 = 1; n > 0} U {0} defined as?The language L is defined as follows:
L = {w = bob1...bn : [2n-i]3 = 1; n > 0} U {0}
where b represents either 0 or 1, i is the position of the first occurrence of the letter b in w (i.e., the index of the first occurrence of "bob" in w), and [x]3 denotes the remainder of x when divided by 3 (i.e., the residue of x modulo 3).
In other words, L is the set of all binary strings that contain the substring "bob" and satisfy the condition that the residue of 2n-i modulo 3 is 1, where n is the number of characters after the first occurrence of "bob".
The language L also includes the string "0" as a special case.
For example, the following strings are in L: "bob1", "bob100", "1101bob010", "00101bob1000", "0".
The following strings are not in L: "0bob", "01bob0", "bob010", "0101bob0", "111".
Learn more about Language L
brainly.com/question/30548874
#SPJ11
table shows the age, in years, of employees in a company.
Age (a) in years
Frequency
18 < a < 20
20 < a < 22
22 < a < 24
24 < a < 26
26 ≤ a
3
2
7
8
O
a) Find the modal class interval. 24..
26
b) Work out an estimate of the mean age of these employees.
Answers
Considering the given table, we have that:
a) The modal class is 24-26.
b) The estimate of the mean is of 23 years.
What is the modal class of a frequency table?The modal class of a frequency table is the class that has the most observations. In this problem, the class is of 24-26, as it has 8 observations, being the largest number.
What is the mean of a discrete distribution?The expected value of a discrete distribution is given by the sum of each outcome multiplied by it's respective probability.
From the frequency table, consisting of 20 observations, a discrete distribution can be built, considering the half-way point of each interval. Then:
P(X = 19) = 3/20 = 0.15.P(X = 21) = 2/20 = 0.1.P(X = 23) = 7/20 = 0.35.P(X = 25) = 8/20 = 0.4.Then the estimate of the mean is:
E(X) = 0.15 x 19 + 0.1 x 21 + 0.35 x 23 + 0.4 x 25 = 23 years.
More can be learned about the mean of a discrete distribution at https://brainly.com/question/24628525
#SPJ1
write the equation of a line in slope intercept form y=mx+b m=6, (0,5)
Answers
Answer:
m is the slope so plug in y=6x+b
and b is the y intercept so the equation is y=6x+5
Step-by-step explanation:
can someone help me with this please

Answers
Answer:
Step-by-step explanation:
Answer is 30
help me plssssssssssssssssssssssssssssssssssssssssss
and please give explanation


Answers
[1] H 2.4
Let us turn the pictures into equations, using the key given. Then, we will solve.
x + x + \(\frac{1}{4}\)x + 1 + 1 + 1 = x + x + x + \(\frac{1}{2}\)x
2x + \(\frac{1}{4}\)x + 3 = 3x + \(\frac{1}{2}\)x
\(\frac{9}{4}\)x + 3 = \(\frac{7}{2}\)x
3 = \(\frac{5}{4}\)x
x = 2.4
[2] J
We can tell the first two options are incorrect because there was a change in size, not position.
Option H would make the shape bigger, but it becomes larger. This means the answer is option J.
please help on this ill give braneliest

Answers
Answer:
-2.5
Step-by-step explanation:
25/-10 = -2.5
20/-8 = 2.5
10/-4 = 2.5
-5/2 = 2.5
so the answer is -2.5
Can I pls have brainliest
r/2=(r-4)/7 how do i solve this?
Answers
Thx hope it helps