−9x+y=10 10x−y=−9 What is the resulting equation?
Answers
Answer:
x=1, y=19. (1, 19).
Step-by-step explanation:
-9x+y=10
10x-y=-9
--------------
x=1
10(1)-y=-9
10-y=-9
y=10-(-9)=10+9=19
Answer: I was kind of confused but here: x=3, y=21. if i am wrong try to be more elaborate and i will try to help
Related Questions
Find the volume of a cone with a base radius of 6 m and a height of 9 m . Write the exact volume in terms of pi , and be sure to include the correct unit in your answer.
Answers
Answer:
108π
Step-by-step explanation:
The formula for the volume of a cone is:
V = (1/3)πr^2h
where r is the radius of the base and h is the height.
Plugging in the given values, we get:
V = (1/3)π(6^2)(9)
V = (1/3)π(36)(9)
V = (1/3)π(324)
V = 108π
Therefore, the exact volume of the cone is 108π cubic meters.
the very possible foods company makes vegan versions of burgers, hot dogs, and chicken wings, and they offer two platters. platter a consists of $1$ burger, $3$ hot dogs, and $5$ chicken wings, which costs $\$16.$ platter b consists of $2$ burgers, $1$ hot dog, and $8$ chicken wings, which costs $\$20.$
Answers
The minimum cost to meet the minimum requirements is $1280.
To determine the minimum cost, we need to calculate the number of platters required to meet the minimum requirements for each item (hamburgers, hot dogs, and chicken wings) and then multiply it by the cost of each platter.
Let's calculate the number of platters required for each item:
For hamburgers:
80 hamburgers / 1 burger per platter = 80 platters
For hot dogs:
95 hot dogs / 1 hot dog per platter = 95 platters
For chicken wings:
380 chicken wings / 5 chicken wings per platter = 76 platters
Now, let's calculate the cost:
For Platter A:
80 platters * $16 per platter = $1280
For Platter B:
95 platters * $20 per platter = $1900
The minimum cost would be the lower of the two costs, which is $1280. Therefore, the minimum cost to meet the minimum requirements is $1280.
To know more about minimum cost, refer here:
https://brainly.com/question/30461381
#SPJ4
Complete Question:
The Very Possible Foods Company makes vegan versions of hamburgers, hot dogs, and chicken wings, and they offer two platters. Platter A consists of 1 burger, 3 hot dogs, and 5 chicken wings, which costs $16. Platter B consists of 2 burgers, 1 hot dog, and 8 chicken wings, which costs $20.
A barbecue organizer requires 80 hamburgers, 95 hot dogs, and 380 chicken wings. (There can be leftovers, but these are the minimum requirements.) What is the minimum cost (in dollars)?
Use the given transformation to evaluate the integral. double integral 9xy dA R , where R is the region in the first quadrant bounded by the lines y = 2 3 x and y = 3x and the hyperbolas xy = 2 3 and xy = 3; x = u/v, y = v
Answers
It looks like the boundaries of \(R\) are the lines \(y=\dfrac23x \) and \(y=3x\), as well as the hyperbolas \(xy=\frac23\) and \(xy=3\). Naturally, the domain of integration is the set
\(R = \left\{(x,y) ~:~ \dfrac{2x}3 \le y \le 3x \text{ and } \dfrac23 \le xy \le 3 \right\}\)
By substituting \(x=\frac uv\) and \(y=v\), so \(xy=u\), we have
\(\dfrac23 \le xy \le 3 \implies \dfrac23 \le u \le 3\)
and
\(\dfrac{2x}3 \le y \le 3x \implies \dfrac{2u}{3v} \le v \le \dfrac{3u}v \implies \dfrac{2u}3 \le v^2 \le 3u \implies \sqrt{\dfrac{2u}3} \le v \le \sqrt{3u}\)
so that
\(R = \left\{(u,v) ~:~ \dfrac23 \le u \le 3 \text{ and } \sqrt{\dfrac{2u}3 \le v \le \sqrt{3u}\right\}\)
Compute the Jacobian for this transformation and its determinant.
\(J = \begin{bmatrix}x_u & x_v \\ y_u & y_v\end{bmatrix} = \begin{bmatrix}\dfrac1v & -\dfrac u{v^2} \\\\ 0 & 1 \end{bmatrix} \implies \det(J) = \dfrac1v\)
Then the area element under this change of variables is
\(dA = dx\,dy = \dfrac{du\,dv}v\)
and the integral transforms to
\(\displaystyle \iint_R 9xy \, dA = \int_{2/3}^3 \int_{\sqrt{2u/3}}^{\sqrt{3u}} \frac{dv\,du}v\)
Now compute it.
\(\displaystyle \iint_R 9xy \, dA = \int_{2/3}^3 \ln|v|\bigg|_{v=\sqrt{2u/3}}^{v=\sqrt{3u}} \,du \\\\ ~~~~~~~~ = \int_{2/3}^3 \ln\left(\sqrt{3u}\right) - \ln\left(\sqrt{\frac{2u}3}\right) \, du \\\\ ~~~~~~~~ = \frac12 \int_{2/3}^3 \ln(3u) - \ln\left(\frac{2u}3\right) \, du \\\\ ~~~~~~~~ = \frac12 \int_{2/3}^3 \ln\left(\frac{3u}{\frac{2u}3}\right) \, du \\\\ ~~~~~~~~ = \frac12 \ln\left(\frac92\right) \int_{2/3}^3 du \\\\ ~~~~~~~~ = \frac12 \ln\left(\frac92\right) \left(3-\frac23\right) = \boxed{\frac76 \ln\left(\frac92\right)}\)
2. Let y₁(x) = e-*cos(3x) be a solution of the equation y(4) + a₁y (3³) + a₂y" + a3y + ay = 0. If r = 2-i is a root of the characteristic equation, a₁ + a2 + a3 + as = ? (a) -10 (b) 0 (c) 17
Answers
The value of a₁ + a₂ + a₃ + aₛ is 16.
How to find the sum of a₁, a₂, a₃, and aₛ?Given that y₁(x) =\(e^{(-cos(3x))\) is a solution of the differential equation y⁽⁴⁾ + a₁y⁽³⁾ + a₂y″ + a₃y + ay = 0, we can conclude that the characteristic equation associated with this differential equation has roots corresponding to the exponents in the solution.
We are given that r = 2 - i is one of the roots of the characteristic equation. Complex roots of the characteristic equation always occur in conjugate pairs.
Therefore, the conjugate of r is its complex conjugate, which is 2 + i.
The characteristic equation can be expressed as (x - r)(x - 2 + i)(x - 2 - i)(x - s) = 0, where s represents the remaining root(s).
Since r = 2 - i is a root, we can conclude that its conjugate, 2 + i, is also a root. This means that (x - 2 + i)(x - 2 - i) = (x - 2)² + 1 = x² - 4x + 5 is a factor of the characteristic equation.
To find the sum of the remaining roots, we equate the coefficients of the remaining factor (x - s) to zero. Expanding the factor gives us x² - (4 + a₃)x + (5a₃ + aₛ) = 0.
By comparing coefficients, we find that -4 - a₃ = 0, which implies a₃ = -4. Furthermore, since the sum of the roots of a quadratic equation is equal to the negation of the coefficient of x, we can conclude that aₛ = -5a₃ = 20.
Therefore, the sum of a₁, a₂, a₃, and aₛ is a₁ + a₂ + a₃ + aₛ = 0 + 0 - 4 + 20 = 16.
Learn more about differential equation
brainly.com/question/32538700
#SPJ11
5. The first five terms of a sequence are -7.7, -7.4, -7.1, -6.8, -6.5.
a. Find an expression for the nth term.
Answers
The expression of the nth term of the given sequence is
-7.7 + (n - 1)0.3
What is an arithmetic sequence?It is a sequence where the difference between each consecutive term is the same.
Example:
2, 4, 6, 8, 10 is an arithmetic sequence.
We have,
-7.7, -7.4, -7.1, -6.8, -6.5
This is an arithmetic sequence.
Now,
a = -7.7
d = -7.4 + 7.7 = 0.3
The nth term of an arithmetic sequence.
= a + (n - a)d
Now,
a + (n - a)d
= -7.7 + (n - 1)0.3
Thus,
The nth term is -7.7 + (n - 1)0.3.
Learn more about arithmetic sequence here:
https://brainly.com/question/10396151
#SPJ1
One indicator that a pediatrician will use to diagnose an infant with "failure to thrive is a weight below the 5th percentile for the baby's age Explain what this mean
Choose the correct answer below
A. Aweight below the 5th percentile means that the baby's weight is less than 5% of the mean weight for all babies of that age
B. A weight below the 5th percentile means that the baby's weight is less than 95% of the mean weight for all babies of that age
C. A weight below the 5th percentile means that the baby's weight is lower than at least 95% of babies that age
D. A weight below the 5th percentile means that the baby's weight is lower than at least 5% of babies that age
Answers
Option A is correct. A weight below the 5th percentile indicates that the baby's weight is less than 5% of the average weight for infants of the same age.
Percentiles are statistical measures used to compare an individual's measurements to a larger population. In this case, the weight percentile indicates how a baby's weight compares to other babies of the same age. The 5th percentile means that the baby's weight is lower than 95% of babies in that age group. Option A correctly states that a weight below the 5th percentile means the baby's weight is less than 5% of the mean weight, indicating that the baby's weight is significantly lower than the average weight for infants of that age.
Learn more about infant weight click here:
brainly.com/question/30227299
#SPJ11
Coins are placed into a treasure chest, and each coin has a radius of 1.4 inches and a height of 0.0625 inches. If there are 230 coins inside the treasure chest, how many cubic inches of the treasure chest is taken up by the coins? Round to the nearest hundredth and approximate using π = 3.14.
Answers
Answer: 32.2 cubic inches
Step-by-step explanation:
The volume of one coin can be calculated using the formula for the volume of a cylinder: V = πr^2h, where r is the radius and h is the height.
Substituting the given values, we get:
V = π(1.4)^2(0.0625)
V ≈ 0.14 cubic inches (rounded to the nearest hundredth)
To find the total volume of all the coins, we can multiply the volume of one coin by the number of coins:
Total volume = 230 × 0.14
Total volume ≈ 32.2 cubic inches (rounded to the nearest hundredth)
Therefore, the coins take up approximately 32.2 cubic inches of the treasure chest.
one of the biggest ethical issues many marketers face today relates to _____________.
Answers
One of the biggest ethical issues many marketers face today relates to consumer privacy and data protection.
In today's digital age, marketers have access to vast amounts of consumer data, including personal information and online behavior. The ethical issue arises when marketers collect, use, and share this data without adequate transparency, consent, or protection of consumer privacy. It raises concerns about invasion of privacy, unauthorized data sharing, and potential misuse of personal information for targeted advertising or other purposes.
Marketers are increasingly under scrutiny to ensure ethical practices in data collection, storage, and usage, balancing the need for effective marketing strategies with respect for individual privacy rights. Failure to address these ethical concerns can lead to loss of trust, reputational damage, and legal consequences for companies. Therefore, marketers must navigate these ethical challenges by adopting transparent and responsible data practices, respecting consumer choices, and implementing robust privacy and security measures.
To know more about ethical issues,
https://brainly.com/question/32499544
#SPJ11
the main sailboat has the dimensions shown in figure at the right . what is the height of the main sail? Then round to the nearest tenth as needed .)

Answers
Answer:
h = 14.5 ft
Step-by-step explanation:
Apply trigonometric ratio formula to find h:
reference angle = 46°
Opposite side = h
Adjacent side = 14 ft
Thus:
Tan 46 = h/14
Multiply both sides by 14
14*tan 46 = h
h = 14.4974243
h = 14.5 (nearest tenth)
PLEASE HELP ASAP DUE TOMORROW!! IF YOU HELP ME I WILL MARK YOU AS BRAINLIEST AND XTRA POINTS!! PLEASE HELP! LOTS OF LOVE!!!


Answers
Answer:
Step-by-step explanation:
To find the speed of a cyclist, divide the distance traveled by the time taken.
In this case, the speed is:
3.75 miles ÷ 0.3 hours = 12.5 miles per hour (mph)
So, the cyclist was traveling at a speed of 12.5 mph.
Answer:
Step-by-step explanation:
Answer should be 12.5 mph.
Please find the limit. Show work and explain in detail. Thank you!
sin e 37. Lim 0-0 sin 20
Answers
The expression sin(e^37) does not have a well-defined limit as x approaches 0 from the left side since the argument e^37 is not an angle and is a constant.
To find the limit of the function sin(e^37) as x approaches 0 from the left side, we need to evaluate the limit and analyze the behavior of the function near 0.
The expression sin(e^37) represents the sine of a very large number, approximately equal to 5.32048241 × 10^16. The sine function oscillates between -1 and 1 as the input increases, but it does so in a periodic manner.
As x approaches 0 from the left side (x < 0), the function sin(e^37x) will oscillate rapidly between -1 and 1. However, since the argument of the sine function (e^37) is an extremely large constant, the oscillations will occur at a much higher frequency.
To calculate the limit, we can directly evaluate the function at x = 0 from the left side.
sin(e^37 * 0) = sin(0) = 0.
Therefore, the limit of sin(e^37) as x approaches 0 from the left side is equal to 0.
Learn more about limit here:-
https://brainly.com/question/29795597
#SPJ11
how much interest earned on 124 ar 4% for one year
Answers
The principal amount is 124
The interest rate is 4% [in decimal, 4% is 4/100 = 0.04]
To get the interest amount, we mutiply the principal with the interest rate (in decimal).
The answer is:
\(124\cdot0.04=4.96\)Use the models to complete the statement. The first model has 1 shaded square and 5 unshaded squares. The second model has 2 shaded squares and 4 unshaded squares.

Answers
The fraction is 1/6 is less than 2/6.
Less than is the answer
How to use the models to complete the statement?A fraction is used to represent the portion/part of the whole thing. It represents the equal parts of the whole.
From the image, the fraction to the left is 1/6 and the fraction to the right is 2/6.
You can think of 1/6 as having a pizza divided into 6 equal portions and you are to pick 1 out of the 6 whereas in the case of 2/6 you are to pick 2 out of the 6. You will notice that you have less pizza in 1/6 than 2/6.
Thus, 1/6 is less than 2/6
Learn more about fractions on:
brainly.com/question/11562149
#SPJ
meaning of primary school
Answers
Answer:
primary school is a primary school
Answer:the meaning of primary school is elementary school basically grades Kinder-5th grade
Step-by-step explanation:
if you have a pool that holds 25 3/4 gallons of water and you drain 1 5/6 how much water will remain??
Answers
Result in decimals: 23.92
Explain how
you know you would use sine, cosine or tangent to
solve this. Explain thorougly
C
X
10
B В

Answers
Answer:
To solve for x, I would use Cosine.
This is because cosine holds the ratio of adjacent/hypotenuse. Based on the diagram, we can see that HYPOTENUSE = x, so we are solving for x. We know the angle, is 17 degrees. Lastly, we know the triangle leg ADJACENT to the angle is 10 units long. So we would use cosine, implementing the ratio adjacent/hypotenuse. Solving this, we would use cos(17)=10/x. Then our goal is to isolate x, so cos(17)=10/x becomes cos(17)*x=10, we are still trying to isolate x, so, x=10/cos(17). Therefore, our answer x = 10.457 units. cosine would be the best way to go.
Step-by-step explanation:
How would I solve this and what’s the answer

Answers
Step-by-step explanation:
these 2 parallel lines create similar triangles.
that mags they're is one common scaling factor for the side lengths bergen the 2 triangles.
and that means they must have the same ratio.
the large triangle has the side lengths
24 + 9 = 33
32 + x
the smaller triangle has the corresponding side lengths
24
32
so, the equal ratios are
24/33 = 32/(32+x)
24(32 + x) = 32×33
32 + x = 32×33/24 = 4×11 = 44
x = 44 - 32 = 12
What is the value of k in the equation StartFraction k Over 3 EndFraction minus 5 = 34?
A. 11 and one-third
1B. 3
C. 102
D. 117
Answers
Answer:
I think the answer is d
Step-by-step explanation:
Answer:
D.
Step-by-step explanation:

3 cm
20 cm
4 cm
Find the volume of the rectangular prism.
[?] cm
Enter
![3 cm20 cm4 cmFind the volume of the rectangular prism.[?] cmEnter](https://i5t5.c14.e2-1.dev/c-qa-images/contents/attachments/9aWQFK2LT09kXmxBJSYxWiW3KkwjXnUh.png)
Answers
Answer:
240cm^3
Step-by-step explanation:
3cmx20cmx4cm=240cm^3
A typical person begins to lose consciousness if subjected to accelerations greater than about 5 g(49.0 m/s^2) for more than a few seconds. Suppose a 3.00×10^4−kg manned spaceship's engine has an exhaust speed of 2.50×10^3 m/s. What maximum burn rate ∣ΔM/Δt∣ could the engine reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness?
Answers
The maximum burn rate ∣ΔM/Δt∣ that the engine could reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness is approximately 51.0 kg/s.
Acceleration is directly proportional to the force acting on an object. In simple terms, if the force on an object is greater, then it will undergo more acceleration. However, there are limitations to the acceleration that can be tolerated by the human body. At about 5 g (49.0 m/s2) for more than a few seconds, an average person starts to lose consciousness. Let's use this information to answer the given question.
Let the maximum burn rate |ΔM/Δt| that the engine could reach before the ship's acceleration exceeded 5 g be x.
Let the mass of the spaceship be m and the exhaust speed of the engine be v.
Using the formula for the thrust of a rocket,
T = (mv)e
After substituting the given values into the formula for thrust, we get:
T = (3.00 × 104)(2.50 × 103) = 7.50 × 107 N
Therefore, the acceleration produced by the engine, a is given by the formula below:
F = ma
Therefore,
a = F/m= 7.50 × 107/3.00 × 104= 2.50 × 103 m/s²
The maximum burn rate that the engine could reach before the ship's acceleration exceeded 5 g is equal to the acceleration that would be produced by a maximum burn rate. Therefore,
x = a/5g= 2.50 × 103/(5 × 9.8)≈ 51.0 kg/s
Therefore, the maximum burn rate ∣ΔM/Δt∣ that the engine could reach before the ship's acceleration exceeded 5 g and its human occupants began to lose consciousness is approximately 51.0 kg/s.
Learn more about maximum burn rate
https://brainly.com/question/29328145
#SPJ11
99% of all confidence intervals with a 99% confidence level should contain the population parameter of interest. true or false
Answers
The statement that 99% of all confidence intervals with a 99% confidence level should contain the population parameter of interest is false.
A confidence interval (CI) is essentially a range of estimates for an unknown parameter in frequentist statistics. The most frequent confidence level is 95%, but other levels, such 90% or 99%, are infrequently used for generating confidence intervals.
The confidence level is a measurement of the proportion of long-term associated CIs that include the parameter's true value. This is closely related to the moment-based estimate approach.
In a straightforward illustration, when the population mean is the quantity that needs to be estimated, the sample mean is a straightforward estimate. The population variance can also be calculated using the sample variance. Using the sample mean and the true mean's probability.
Hence we can generally infer that the given statement is false.
To learn more about confidence intervals visit:
https://brainly.com/question/24131141
#SPJ4
Math the following measurements
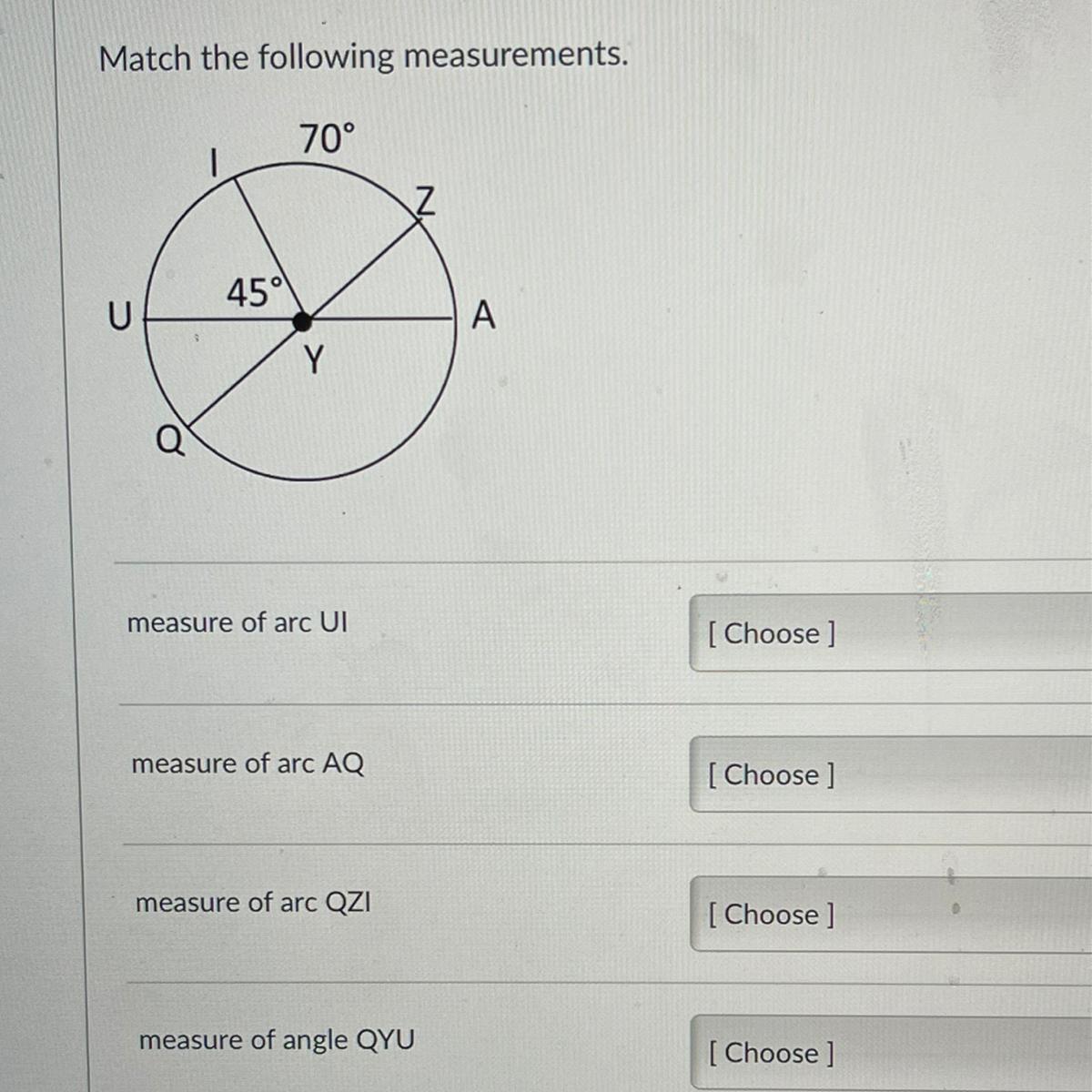
Answers
Answer:
UI=45
AQ=115
QZI=175
QYU=65
is 4x^2 + 8 =12 a linear equation
Answers
No, \(4x^{2} +8=12\) is not a linear equation
What is linear equation?
An equation is said to be linear if the maximum power of the variable is consistently 1. Another name for it is a one-degree equation. A linear equation with one variable has the conventional form Ax + B = 0. In this case, the variables x and A are variables, whereas B is a constant. A linear equation with two variables has the conventional form Ax + By = C. Here, the variables x and y, the coefficients A and B, and the constant C are all present.
No, \(4x^{2}+8=12\\4x^{2} -4=0\)is not a linear equation because An equation is said to be linear if the maximum power of the variable is consistently 1.
This is a quadratic equation, because quadratic equation has a maximum power of 2.
To learn more about linear equation checkout https://brainly.com/question/29739212
#SPJ1
Problem 4-7 Calculating the Number of Periods [LO 4] At 5.25 percent interest, how long does it take to double your money? Note: Do not round intermediate calculations and round your answer to 2 decimal places, e.9., 32.16. At 5.25 percent interest, how long does it take to quadruple your money? Note: Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.
Answers
The number of periods is approximately 26.98.
To calculate the number of periods it takes to double your money at 5.25 percent interest, you can use the formula for compound interest:
Future value = Present value * (1 + interest rate) ^ number of periods
In this case, the future value is twice the present value, so the equation becomes:
2 = 1 * (1 + 0.0525) ^ number of periods
To solve for the number of periods, you can take the logarithm of both sides:
log(2) = log((1 + 0.0525) ^ number of periods)
Using the logarithmic properties, you can bring the exponent down:
log(2) = number of periods * log(1 + 0.0525)
Finally, you can solve for the number of periods:
number of periods = log(2) / log(1 + 0.0525)
Using a calculator, the number of periods is approximately 13.27.
To calculate the number of periods it takes to quadruple your money at 5.25 percent interest, you can follow the same steps as above, but change the future value to four times the present value:
4 = 1 * (1 + 0.0525) ^ number of periods
Solving for the number of periods using logarithms:
number of periods = log(4) / log(1 + 0.0525)
Using a calculator, the number of periods is approximately 26.98.
To know more about periods visit:-
https://brainly.com/question/23532583
#SPJ11
In parallelogram GRAM, m

Answers
Answer:
Step-by-step explanation:

Each question Sandra answers incorrectly changes her overall score by - points. Sandra's
overall score was - 41 points, and then she answered the last question incorrectly. What
was Sandra's final score?
-33
3.
DO
Answers
Answer: you can't really answer this because it's not telling me how many questions she answered so I don't know how many questions there are to decide how many points there are for each question but I'll give it a try.
Step-by-step explanation:
41 - 8 = 33 that's all I got and also next time make sure you put the answer choices on that too if there are any
What is the equation in slope-intercept form of the line that passes through the point(5,0) and is parallel to the line represented by y = 1.2 x + 3.8?
Answers
three more than eight times a number equal to 19
Answers
If you need x, then it’s 2 because
8(2) + 3 = 19
if that is = a, find the value of a + 1 over a
\(3 - \sqrt{5} \)
Answers
Answer:
7+√5/4
Step-by-step explanation:
if that is = a, find the value of a + 1 over a
Given that a = 3 - √5
a+1/1 = (3-√5)+1/3 - √5
4-√5/3 - √5
Rationalize
4-√5/3 - √5 * 3+√5/3 + √5
= 12 +4√5-3√5-√25/9-5
= 12+√5-5/4
= 7+√5/4
Hence the requred answer is 7+√5/4
determine the periodic solutions, if any, of the system x˙ = y x p x 2 y 2 (x 2 y 2 − 2), y˙ = −x y p x 2 y 2 (x 2 y 2 − 2).
Answers
The periodic solutions of the system are:
(0, 0),
(±√2, ±√2).
These points represent periodic orbits in the phase space of the system.
To determine the periodic solutions, if any, of the system:
ẋ = yx^p(x^2y^2 - 2),
ẏ = -xy^p(x^2y^2 - 2),
we need to find values of x and y for which the derivatives ẋ and ẏ are equal to zero simultaneously. These points represent potential periodic solutions.Setting ẋ = 0 and ẏ = 0, we have:
0 = yx^p(x^2y^2 - 2),
0 = -xy^p(x^2y^2 - 2).
From the first equation, we can see that either y = 0 or x^2y^2 - 2 = 0.
If y = 0, then the second equation implies that x = 0. Therefore, (0, 0) is a solution.
If x^2y^2 - 2 = 0, then x^2y^2 = 2.
Taking the square root of both sides, we get xy = ±√2.Considering the second equation, we have -xy^p(x^2y^2 - 2) = 0.
Substituting xy = ±√2, we find that this equation holds true.
For such more questions on Periodic orbits:
https://brainly.com/question/13501470
#SPJ11