9x - 13 =32 what is x
Answers
Answer:
Hi!
\(x=5\)
Step-by-step explanation:
\(9x-13+13=32+13\\9x=45\\\frac{9x}{9}=\frac{45}{9}\\=5\)
Answer:
the answer is 5
Step-by-step explanation:
9 x 5 -13= 32
Related Questions
Are 2b+ b and 3b equivalent expressions?
Answers
Answer:
yes
Step-by-step explanation:
2b+b=3b because2+1 = 3
Answer:
the answer is yes
Step-by-step explanation:
yes it is equivalent expression because 2b+b and 3b have the same value and length or numerator which equals yes.
Is this reasoning valid or not? If it is July then it is summer, and it’s not July therefore it’s not summe.
Answers
Answer:Not valid
Step-by-step explanation:
hope this helps!!!!!!!!!!!!!!!!!!!!!!!!!
I really need help. Giving brainliest to the real answer. Please my grade closes tomorrow (don’t mind the writing I tried doing it myself)
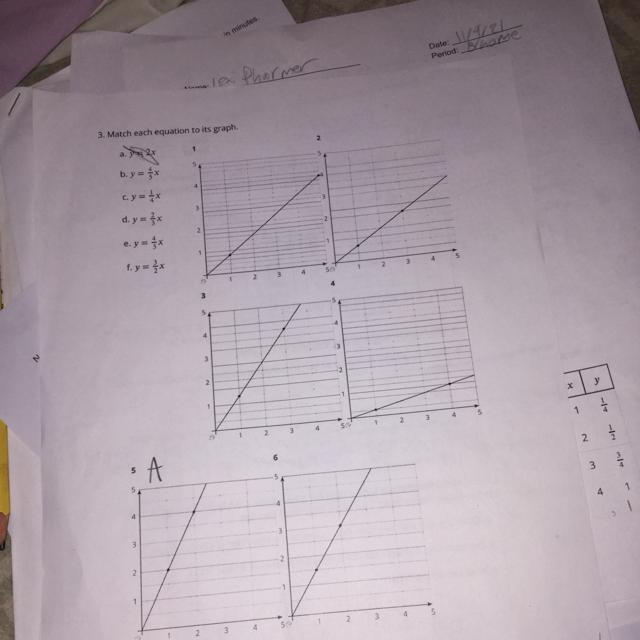
Answers
Answer:
1. B
2. D
3. E
4. C
5. A
6. F
How do I solve for this?

Answers
Answer: \(cosx =- \sqrt{ 1 - sin^2x}\)
Step-by-step explanation:
Generally speaking; \(cos^2x + sin^2x = 1\)
rearranging this gives us all sorts of cool things.
for now, we will use: \(cosx = \sqrt{ 1 - sin^2x}\)
This however, is general.
In the third quadrant, cosine is negative. So cosx in QIII will be:
\(cosx =- \sqrt{ 1 - sin^2x}\)
and thats the answer :)
Solve
7x = 42
x = 294
x = 35
x = 6
x = 49
Answers
Answer:49
Step-by-step explanation:
Answer:
x = 6
Step-by-step explanation:
7 x 6 = 42 making the answer 6 true.
What is 9/24 lowest term
Answers
The lowest term of the fraction 9/24 is 3/8.
To find the lowest term of a fraction, we need to simplify it by dividing both the numerator and denominator by their greatest common divisor (GCD). In the case of 9/24, we can see that both numbers are divisible by 3. By dividing both 9 and 24 by 3, we get the simplified fraction 3/8.
Simplifying fractions to their lowest terms is important because it gives us the simplest and most compact representation of the ratio between the numerator and the denominator. It provides a clearer understanding of the relationship between the parts of the fraction.
In this example, by simplifying 9/24 to 3/8, we can see that the fraction represents a ratio of 3 parts to 8 parts, indicating that for every 3 units, there are 8 units. This simplified form allows for easier comparisons and calculations.
It's worth noting that simplifying fractions is not just about dividing by the GCD. It involves finding the common factors and dividing them out until no further simplification is possible. This process ensures that the fraction is in its lowest terms, providing a more concise and meaningful representation.
To learn more about the division;
https://brainly.com/question/13263114
#SPJ1
Hank made payments of $219 per month at the end of each month for 30 years to purchase a piece of property. He promptly sold it for $195,258. What interest rate, compounded monthly, would he need to earn on an ordinary annuity for a comparable rate of return?
Answers
To achieve a comparable rate of return, Hank would need to earn an interest rate of approximately 0.86% per month, compounded monthly on his ordinary annuity.
To find the interest rate, compounded monthly, that Hank would need to earn on an ordinary annuity for a comparable rate of return, we can use the present value formula for an ordinary annuity.
First, let's calculate the present value of Hank's payments. He made payments of $219 per month for 30 years, so the total payments amount to $219 * 12 * 30 = $78840.
Now, we need to find the interest rate that would make this present value equal to the selling price of the property, which is $195,258.
Using the formula for the present value of an ordinary annuity, we have:
PV = P * (1 - (1+r)\(^{(-n)})\)/r,
where PV is the present value, P is the payment per period, r is the interest rate per period, and n is the number of periods.
Plugging in the values we have, we get:
$78840 = $219 * (1 - (1+r)\({(-360)}\))/r.
Solving this equation for r, we find that Hank would need to earn an interest rate of approximately 0.86% per month, compounded monthly, in order to have a comparable rate of return.
For more questions on interest rates
https://brainly.com/question/31261623
#SPJ8
What is the measure of angle y In this figure?
Enter your answer in the box.
y=____

Answers
Since angle y is directly across from 163* it is equal to that angle.
three sides of triangle is x cm y cm z cm its perimeter and semi perimeter
Answers
Answer:
Step-by-step explanation:
Perimeter:
\(P=(x+y+z) \ cm\)
Semi-perimeter:
\(SP=\frac{1}{2} (x+y+z) \ cm\)
simplify 3 / 8 (–2 / 7 +(–3 / 8 ×2 / 5)
Answers
Answer:
so the answer is 0.16339

what is the variable "d" equal to in the equation 2d + 13
Answers
Answer:
d=-6.5
Step-by-step explanation:
2d+13=0
2d=-13
d= -13/2
d=-6.5
Explain with steps please and thank you! :)

Answers
Using the information in the given diagram, the value of the missing angle is: m∠1 = 75°
How to find the missing angle?The transverse line theorem states that If two parallel lines are cut by a transversal, then corresponding angles are congruent. Two lines cut by a transversal are parallel IF AND ONLY IF corresponding angles are congruent.
Now, when we draw a horizontal line parallel to lines a and b and directly cutting across the vertex of angle 1, we can see that angle 1 will be composed of two angles.
Now, for the transverse line theorem we can say that:
Angle 1 will be composed of two angles namely:
48 degrees and (180 - 153) degrees.
Thus:
m∠1 = 48° + 27°
m∠1 = 75°
Read more about Missing Angle at: https://brainly.com/question/28293784
#SPJ1
Soryyyyyyyyyyyyyy this one to

Answers
The two congruent sides will have congruent angles. One angle measurement is given. Triangle angles equal 180.
Take 180 and subtract the given angle 93.5. Then divide by 2 to get the measurements x and the other unknown.
180 - 93.5 = 86.5
86.5/2 = 43.25
Help me answer this for brainliest

Answers
Answer:
question 1(2)
answer 4
question 2(3)
answer 1
question 3(4)
(a)6; factored
(b)7; factored
c(8); factored
1/3x+6=-8
solve for x
Answers
Answer:
X: should = 0.7, you already have 1/3 , and + 6= 8. take 8-6 = 2: 2- 1/3 = (0.7) so the abswer should be X= 0.7.
There was a girl named sally n she was driving
to her parents house going a speed of 60 miles
every 100 minutes. If it took her 2 hours to get
there and she got there at 6:30 ok what time did
she start
Answers
Answer:
She started at 4:30
Step-by-step explanation:
6:30 - 2hr = 4:30
Tell whether the ratios are equivalent: 3 miles to 4 minutes and 9 miles to 12 miles. Show your work.
Answers
Answer:
they are
Step-by-step explanation:
divide 12*4=3
9*3=3
same ratio
The conditional statement below is true. If possible, write the biconditional statement.
If 2x = 18, then x = 9.
Answers
The biconditional statement for the given conditional statement would be:
2x = 18 if and only if x = 9.
The given conditional statement "If 2x = 18, then x = 9" can be represented symbolically as p → q, where p represents the statement "2x = 18" and q represents the statement "x = 9".
To form the biconditional statement, we need to determine if the converse of the conditional statement is also true. The converse of the original statement is "If x = 9, then 2x = 18". Let's evaluate the converse statement.
If x = 9, then substituting this value into the equation 2x = 18 gives us 2(9) = 18, which is indeed true. Therefore, the converse of the original statement is true.
Based on this, we can write the biconditional statement:
2x = 18 if and only if x = 9.
The biconditional statement implies that if 2x is equal to 18, then x must be equal to 9, and conversely, if x is equal to 9, then 2x is equal to 18. The biconditional statement asserts the equivalence between the two statements, indicating that they always hold true together.
In summary, the biconditional statement is a concise way of expressing that 2x = 18 if and only if x = 9, capturing the mutual implication between the two statements.
for such more question on conditional statement
https://brainly.com/question/27839142
#SPJ8
f(x)= 5x+7
g(x) =3x-1
find: f(g(x))
Answers
Answer: 15x+2
Step-by-step explanation:
f(g(x))=f(3x-1)=5(3x-1)+7=15x-5+7=15x+2
What is the base of a triangle with an area of 207 square inches and a height of 18 inches?
Provide your answer below:
Answers
what does the word "baking" means and of which language,this word belongs to?
Answers
Answer:to cook something to a certain degree and it belongs to English which derives from the old english version “bacan”
Step-by-step explanation:
If m<2 = 48° and m<3 = 76, determine m<1.
Answers
Answer:
do you have a screenshot of the angle or something? is it a triangle or another shape? anyhwhooo I believe your answer should be 56°
Step-by-step explanation:
48° + 76° = 124°
180° - 124° = 56°
so your answer is 56°
You are driving on a road that has a 12% uphill grade. This means that the slope of the road is 12/100. Approximate the amount of vertical change in your position when you drive 200 feet
Answers
Answer:
24
Step-by-step explanation:
Therefore our proportion is: (where x is the "vertical" rise)
Slope is defined as rise over fun so....
12/100 = x/200
(12*200)/100 = x
24 feet = x
In △JKL , if m∠ J < 90° , then ∠K and ∠L are _____
Answers
Both angle K and angle L must be acute angles, measuring less than 90 degrees, in order to satisfy the conditions of the given triangle.
In triangle JKL, if angle J is less than 90 degrees, then angle K and angle L are both acute angles.
An acute angle is defined as an angle that measures less than 90 degrees. Since angle J is given to be less than 90 degrees, it is an acute angle.
In a triangle, the sum of the interior angles is always 180 degrees. Therefore, if angle J is less than 90 degrees, the sum of angles K and L must be greater than 90 degrees in order to satisfy the condition that the angles of a triangle add up to 180 degrees.
Hence, both angle K and angle L must be acute angles, measuring less than 90 degrees, in order to satisfy the conditions of the given triangle.
For more questions on triangle
https://brainly.com/question/1058720
#SPJ8
Required Information NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Show that if n is an integer and m+ 5 is odd, then n is even using a proof of contraposition. Rank the options below. We can write n = 2k +1 for some integer k. As n + 5 Is two times an integer, it is even. Assume that n is odd. Thus, if n is odd, then 3 + 5 is even. Then, 13 + 5 = (2K+993 +5=863 +1242 +66+6 = 2(4x3 +672 + 3k + 3).
Answers
If n is an integer and m + 5 is odd, then n must be even.
To prove this statement using contraposition, we need to show that if n is odd, then m + 5 must be even. Assume that n is odd, which means we can write n = 2k + 1 for some integer k.
Then, we can rewrite m + 5 as (2k + 1) + 5 = 2k + 6 = 2(k + 3), which is even.
Therefore, we have shown that if n is odd, then m + 5 is even.
By contraposition, we can conclude that if m + 5 is odd, then n must be even. Overall, the proof uses the fact that odd + odd = even and even + odd = odd, along with the definition of even and odd integers.
For more questions like Contraposition click the link below:
https://brainly.com/question/5306301
#SPJ4
Find the of the slope of the line through (6,-10) and (4,-8)
Answers
Answer:
-1
Step-by-step explanation:
y = mx + c
m is the slope/gradient
to find slope = y2 - y1 / x2 - x1
= -8 - -10 / 4 - 6
m = -1
Given the following sets, find the set (A U B) n (AUC).
U= {1, 2, 3, ..., 10}
A=(2, 5, 7, 10}
B = {1, 2, 3)
C={1, 2, 3, 4, 5}
Answers
The set (A U B) n (A U C) is {2, 5, 7, 10}. A.
To find the set (A U B) n (A U C), we first need to calculate the union of sets A and B, and then calculate the union of that result with set C. Finally, we find the intersection of these two sets.
Set A U B:
The union of sets A and B, denoted as A U B, is the combination of all elements from both sets without any repetitions.
A contains the elements 2, 5, 7, and 10, while B contains the elements 1, 2, and 3.
A U B consists of the elements {1, 2, 3, 5, 7, 10}.
Set (A U B) U C:
Next, we calculate the union of the set (A U B) with set C, denoted as (A U B) U C. A U B contains the elements {1, 2, 3, 5, 7, 10} and C contains the elements {1, 2, 3, 4, 5}.
Taking the union of these two sets results in {1, 2, 3, 4, 5, 7, 10}.
Finding the intersection:
Finally, we find the intersection of (A U B) U C with A U C. A U C consists of the elements {2, 5, 7, 10}.
The intersection of these two sets is the combination of common elements.
The common elements are {2, 5, 7, 10}.
For similar questions on set
https://brainly.com/question/13458417
#SPJ8
Problem of the Day
The tortoise and the hare were arguing: who's the fastest? The tortoise boasted he
could swim 220 miles in 10 hours. The hare bragged he could hop 90 miles in 2 hours.
But who is faster? How can you tell?
Answers
Answer:
hare
Step-by-step explanation:
Their average rates are ...
tortoise: (220 mi)/(10 h) = 22 mi/h
hare: (90 mi)/(2 h) = 45 mi/h
The hare has a faster speed than the tortoise.
You randomly select an integer from 0 to 39 (inclusively) and then randomly select an integer from 0 to 4 (inclusively). What is the probability of selecting a 2 both times? The probability is nothing.
Answers
The correct value of probability of selecting a 2 both times is 1/200.
Let's calculate the correct probability.When randomly selecting an integer from 0 to 39, there is 1 favorable outcome (selecting a 2) out of 40 possible outcomes. Therefore, the probability of selecting a 2 in the first selection is 1/40.
Similarly, when randomly selecting an integer from 0 to 4, there is 1 favorable outcome (selecting a 2) out of 5 possible outcomes. Therefore, the probability of selecting a 2 in the second selection is 1/5.
To find the probability of both events happening (selecting a 2 in both selections), we multiply the individual probabilities:
P(Selecting a 2 both times) = (1/40) * (1/5) = 1/200
Therefore, the probability of selecting a 2 both times is 1/200.We are given two independent events:
Randomly selecting an integer from 0 to 39 (inclusive).
Randomly selecting an integer from 0 to 4 (inclusive).
We want to calculate the probability of selecting a 2 in both selections.
In the first selection, there is only one favorable outcome (selecting a 2)out of 40 possible outcomes (numbers from 0 to 39). Therefore, the probability of selecting a 2 in the first selection is 1/40.
In the second selection, there is again only one favorable outcome (selecting a 2) out of 5 possible outcomes (numbers from 0 to 4). So, the probability of selecting a 2 in the second selection is 1/5.
Since the two events are independent, we can multiply their individual probabilities to find the probability of both events happening.
Probability of selecting a 2 in both selections = (1/40) * (1/5) = 1/200Therefore, the probability of randomly selecting a 2 in both selections is 1/200. This means that out of all possible outcomes, there is a 1 in 200 chance of selecting a 2 in both selections.
Learn more about Probability here:
https://brainly.com/question/23417919
#SPJ8
A pizza is cut into six unequal slices (each cut starts at the center). The largest slice measures 90 degrees: If Larry eats the slices in order from the largest to the smallest, then the number of degrees spanned by a slice decreases at a constant rate. (So the second slice is smaller than the first by a certain number of degrees, then the third slice is smaller than the second slice by that same number of degrees, and so on.)
What is the degree measure of the fifth slice Larry eats?
Can someone explain how they got the answer and what numbers to use?

Answers
9514 1404 393
Answer:
42°
Step-by-step explanation:
The problem tells you the degree measures form an arithmetic progression. The sum of the 6 terms of the progression is 360, and the first term is 90.
The sum of n terms of an arithmetic progression is given by ...
Sn = (a1 +d/2(n -1))n
For Sn = 360, a1 = 90, n = 6, we have ...
360 = (90 +d/2(5))(6)
Dividing by 6 and subtracting 90 gives ...
-30 = 5/2d
Multiplying by 2/5, we find the number of degrees difference to be ...
d = -12
Then the 5th term of the sequence is ...
an = a1 +d(n -1)
a5 = 90 -12(5 -1) = 90 -48 = 42
The 5th slice Larry eats has a measure of 42 degrees.
_____
The slices measure 90, 78, 66, 54, 42, 30 degrees.