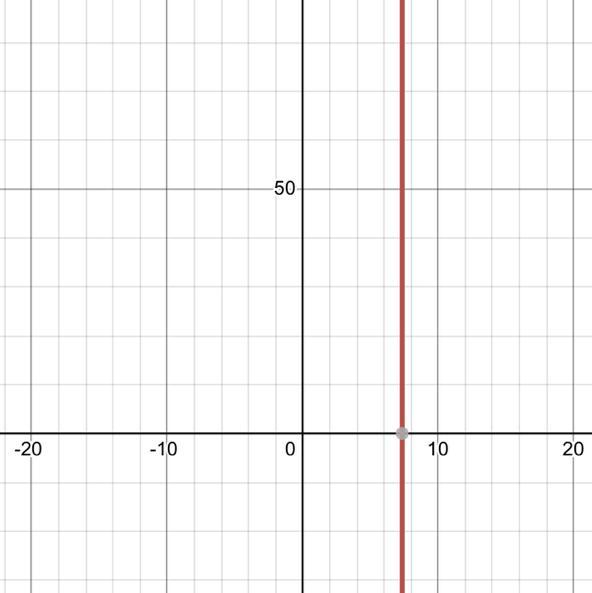
760=100x+25 graphed ?
Answers
Related Questions
Write 7320 correct to one significant figure
Answers
Within the case of 7320, the digit within the tens put is 3, which is less than 5. Hence, we circular down the units digit to 0, and the number gets to be 7300.
Within the handle of adjusting to one noteworthy figure, we ought to see the digit within the tens put (the moment digit from the cleared out) and decide whether to circular up or down. On the off chance that the digit within the tens put is 5 or more prominent, we circular up the units digit. In the event that it is less than 5, we circulate down the units digit.
This streamlines the number and keeps as it were the foremost noteworthy digit, which is 7. Adjusting to one noteworthy figure could be a valuable way to quickly estimate the greatness of a number without requiring to know the correct esteem.
To learn about similar questions visit:
https://brainly.com/question/29005687
#SPJ4
let e be the event where the sum of two rolled dice is greater than 7. list the outcomes in ec
Answers
The event e consists of outcomes where the sum of two rolled dice is greater than 7.
When two dice are rolled, the possible outcomes range from 2 to 12. To determine the outcomes in event e, we need to identify the combinations that yield a sum greater than 7. These combinations are: (6, 2), (6, 3), (6, 4), (6, 5), (5, 3), (5, 4), (5, 5), (4, 4), (4, 5), (3, 5), and (2, 6). Therefore, the outcomes in event e are (6, 2), (6, 3), (6, 4), (6, 5), (5, 3), (5, 4), (5, 5), (4, 4), (4, 5), (3, 5), and (2, 6).
Learn more about outcomes here
https://brainly.com/question/30507347
#SPJ11
Find the value of x in the isosceles triangle shown below.

Answers
Answer:
x = \(\sqrt{26}\)
Step-by-step explanation:
using pythagoras theorem
here \(\sqrt{13}\) and \(\sqrt{13}\) are the legs of the right angled triangle and x is hypotenuse.
a^2 + b^2 = c^2
\((\sqrt{ 13 })^2 + (\sqrt{13})^2 = x^2\)
13 + 13 = x^2
26 = x^2
\(\sqrt{26}\) = x
Answer:
answer would be c
Step-by-step explanation:
hope this helps
the points (4,0) and (3,9) lie on a particular line. which is its equation in slope intercept form of this line
Answers
Answer:
\(y = -9x + 36\)
Step-by-step explanation:
\(\textsf {The slope-intercept form of a line is $y = mx + b$ where m is the slope and b the y-intercept}\\ \\\textsf{Slope is computed using the formula}\)
\(m = \dfrac {(y_{2} - y_{1})} {(x_{2} - x_{1})}\)
\(\sf where \; (x_1,y_1) and (x_2, y_2)\; are\;any\;two\;points\;on\;the\;line\)
\(\textsf{Given that the line passes through (4, 0) and (3, 9) we can compute the slope:}\)
\(m = \dfrac{9 - 0}{3 - 4}\\\\m = \dfrac{9}{-1}\\\\m = -9\)
So the slope of the line is y = -9x + b
We have
y = -9x + b
Add 9x to both sides
y + 9x = -9x + 9x + b
y + 9x = b
switching sides,
b = y + 9x
Plug in the (x, y) values for point (4, 0)
b = 0 + 9(4)
b = 36
So the equation of the line is
\(\boxed{y = -9x + 36}\)
Jimmy was playing a board game with his family. He loses 7 points each minute for 6 minutes in a row. Which of the following sums most accurately models how many points he has in total?
(-7)(-6) = 42
(6)(7) = 42
(-7)(6) = -42
(-6)(7) = -42
Answers
Answer:
(-7)(6) = -42
Step-by-step explanation:
Negative 7 represents the amount of points he loses per positive minute (6)
Mary did not pay last month's credit card bill in full. Below is a list of Mary's daily balances for his last billing cycle.
For 6 days she owed $500.00
For 4 days she owed $350.26
For 7 days she owed $568.45
For 8 days she owed $480.34
For 6 days she owed $649.90
Type your answer.
Answers
500+350.26+568.45+480.34+649.90 = $2548.95
hope it really helps...!!!
a sample of 90 adult randolph county residents showed that 59 own a home. what is the risk of owning a home?
Answers
The risk of owning a home in Randolph County based on the given sample can be calculated as:
Risk of owning a home = Number of residents who own a home / Total number of residents in the sample
Risk of owning a home = 59 / 90
Therefore, the risk of owning a home in Randolph County based on the given sample is approximately 0.656 or 65.6%.
Andre and Elena are each saving money. Andre starts with 100$ in his savings account and adds 5$ per week. Elena starts with 10$ in her savings account and adds 20$ each week. after 4 weeks who has more money in their savings account
Answers
Step-by-step explanation:
let π be the person who has more money
solution
$100+$5+$10+$20
=135
135:π:4
Suppose a department contains 10 men and 15 women. a) How many ways are there to form a committee of 6 people from the department? Explain your answer. b) How many ways are there to form a committee of 6 people from the department, if the number of men in the committee is equal to the number of females in the committee? Explain your answer. c) How many ways are there to form a committee of 6 people from the department, if the number of men in the committee is less than the number of females in the committee? Explain your answer.
Answers
a) The number of ways to form a committee of 6 people from the department is 177,100.
b) The number of ways to form a committee of 6 people with an equal number of men and women is 54,600.
c) The number of ways to form a committee of 6 people with more women than men is 91,455.
a) To form a committee of 6 people from the department, we can choose 6 individuals from a total of 25 people (10 men + 15 women). The order in which the committee members are chosen does not matter, and we are not concerned with any specific positions within the committee. Therefore, we can use the concept of combinations.
The number of ways to choose 6 people from a group of 25 is given by the combination formula:
C(25, 6) = 25! / (6! * (25 - 6)!) = 25! / (6! * 19!) = 177,100
Therefore, there are 177,100 ways to form a committee of 6 people from the department.
b) In this case, we need to choose an equal number of men and women for the committee. We can select 3 men from the available 10 men and 3 women from the available 15 women. Again, the order of selection does not matter.
The number of ways to choose 3 men from 10 is given by the combination formula:
C(10, 3) = 10! / (3! * (10 - 3)!) = 10! / (3! * 7!) = 120
Similarly, the number of ways to choose 3 women from 15 is:
C(15, 3) = 15! / (3! * (15 - 3)!) = 15! / (3! * 12!) = 455
To find the total number of ways to form a committee with an equal number of men and women, we multiply these two combinations:
Total = C(10, 3) * C(15, 3) = 120 * 455 = 54,600
Therefore, there are 54,600 ways to form a committee of 6 people with an equal number of men and women.
c) In this case, we need to form a committee with more women than men. We can choose 1 or 2 men from the 10 available men and select the remaining 6 - (1 or 2) = 5 or 4 women from the 15 available women.
For 1 man and 5 women:
Number of ways to choose 1 man from 10: C(10, 1) = 10
Number of ways to choose 5 women from 15: C(15, 5) = 3,003
For 2 men and 4 women:
Number of ways to choose 2 men from 10: C(10, 2) = 45
Number of ways to choose 4 women from 15: C(15, 4) = 1,365
The total number of ways to form a committee with more women than men is the sum of these two cases:
Total = (Number of ways for 1 man and 5 women) + (Number of ways for 2 men and 4 women)
= 10 * 3,003 + 45 * 1,365
= 30,030 + 61,425
= 91,455
Therefore, there are 91,455 ways to form a committee of 6 people with more women than men.
To know more about number of ways, refer here:
https://brainly.com/question/30649502
#SPJ4
PLLLLLLLLLLLZZZZZZZZZZZZZZZZZZ HHHHHHHHHEEEEEEEEEEEEEELLLLLLLLLLLLLLPPPPPPPPPPPPPP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Here are your answers!
I hope I got it right :(

Answer:
11) 1080°
12) 900°
Step-by-step explanation:
11) the letter T forms an 8-sided figure (octagon)
to find the sum of the interior angles in any shape, use this formula:
(n-2)·180° where 'n' is the number of sides
(8-2)·180 = 6(180) = 1080°
12) this shape has 7 sides so:
(7-2)·180° = 5(180) = 900°
What part of an hour passes between 4:56 p.m. and 5:32 p.m.?
Answers
3/5 part of an hour passes in between two times given.
What is fraction?
A fraction represents a vicinity of a full or, a lot of typically, any variety of equal elements. once spoken in everyday English, a fraction describes what number elements of a precise size there ar,
Main body:
The time given are = 4:56 and 5:32
Total time spent between = 4+ 32
= 36 minutes
Total minutes in 1 hour = 60
So parts spent = 36/60
now simplifying we get.
= 3/5
Hence the answer is 3/5 .
To know more about fraction ., clcik on the link below
https://brainly.com/question/78672
#SPJ4
Ten years ago, the population at Lincoln High School was about 2,000 students. Since then, the population has increased by 25%.
What is the new population now?
Answers
Answer:
2,500 students
Step-by-step explanation:
If the population has increased by 25%, the total population of the school is now 125% of what it used to be. Then to figure it out, you find out 125% of 2000 which is 2,500 students!
(Hope that helps :):):)
What is the volume of the cylinder with height 8m and radius of 5m
Answers
Question :-
What is the volume of a cylinder with a radius of 5 m and a height of 8 m?Answer :-
The volume of a cylinder is 628 m³.\( \rule{180pt}{4pt}\)
Diagram :-
\(\setlength{\unitlength}{1mm}\begin{picture}(5,5)\thicklines\multiput(-0.5,-1)(26,0){2}{\line(0,1){40}}\multiput(12.5,-1)(0,3.2){13}{\line(0,1){1.6}}\multiput(12.5,-1)(0,40){2}{\multiput(0,0)(2,0){7}{\line(1,0){1}}}\multiput(0,0)(0,40){2}{\qbezier(1,0)(12,3)(24,0)\qbezier(1,0)(-2,-1)(1,-2)\qbezier(24,0)(27,-1)(24,-2)\qbezier(1,-2)(12,-5)(24,-2)}\multiput(18,2)(0,32){2}{\sf{5 \: m}}\put(9,17.5){\sf{8 \: m}}\end{picture}\)
Solution :-
As per provided information in the given question, we have been given that the Radius of a cylinder is 5 meters. The height of a cylinder is 8 meters. We have been asked to find the volume of a cylinder.
To calculate the volume of a cylinder, we will apply the formula below :-
\( \bigstar \: \: \: \boxed{ \sf{ \: \: Volume_{(Cylinder)} = \pi r^2 h \: \: }}\)
Substitute the given values into the above formula and solve for Volume :-
\(\sf:\implies Volume_{(Cylinder)} = \pi r^2 h\)
\(\sf:\implies Volume_{(Cylinder)} = (3.14)(5 \: m)^2(8 \: m)\)
\(\sf:\implies Volume_{(Cylinder)} = (3.14)(25 \:m^2)(8 \: m)\)
\(\sf:\implies Volume_{(Cylinder)} = (78.5 \:m^2)(8 \:m)\)
\(\sf:\implies\bold{Volume_{(Cylinder)} = 628 \: m^3}\)
Therefore :-
The volume of a cylinder is 628 m³.\(\\\)
Learn more about the Volume of a Cylinder at https://brainly.com/question/15197979
Have a great day! <33
Finding a Function to Match a Current Grade: 0.0/1.0 Remaining Time: Unlimited Shape For this week's discussion, you are asked to generate a continuous and differentiable function f(x) with the following properties: - f(x) is decreasing at x=−6 - f(x) has a local minimum at x=−3 - f(x) has a local maximum at x=3 Your classmates may have different criteria for their functions, so in your initial post in Brightspace be sure to list the criteria for your function. Hints: - Use calculus! - Before specifying a function f(x), first determine requirements for its derivative f ′
(x). For example, one of the requirements is that f ′
(−3)=0. - If you want to find a function g(x) such that g(−9)=0 and g(8)=0, then you could try g(x)=(x+9)(x−8). - If you have a possible function for f ′
(x), then use the techniques in Indefinite Integrals this Module to try a possible f(x). You can generate a plot of your function by clicking the plotting option (the page option with a "P" next to your function input). You may want to do this before clicking "How Did I Do?". Notice that the label " f(x)= " is already provided for you. Once you are ready to check your function, click "How Did I Do?" below (unlimited attempts). Please note that the bounds on the x-axis go from -6 to 6 .
Answers
To find a function that satisfies the given criteria, we can start by determining the requirements for its derivative, f'(x).
Let's break down the given properties and find the corresponding requirements for f'(x): f(x) is decreasing at x = -6: This means that the slope of the function should be negative at x = -6. Therefore, f'(-6) < 0. f(x) has a local minimum at x = -3: At a local minimum, the slope changes from negative to positive. Thus, f'(-3) = 0. f(x) has a local maximum at x = 3: At a local maximum, the slope changes from positive to negative. Hence, f'(3) = 0.
Now, let's integrate f'(x) to obtain f(x): Integrating f'(x) = -6 < x < -3 will give us a decreasing function on that interval. Integrating f'(x) = -3 < x < 3 will give us an increasing function on that interval. Integrating f'(x) = 3 < x < 6 will give us a decreasing function on that interval. To simplify the process, let's assume that f'(x) is a quadratic function with roots at -6, -3, and 3. We can represent it as: f'(x) = k(x + 6)(x + 3)(x - 3), where k is a constant that affects the steepness of the curve. By setting f'(-3) = 0, we find that k = -1/18.
Therefore, f'(x) = -1/18(x + 6)(x + 3)(x - 3). Integrating f'(x) will give us f(x): f(x) = ∫[-6,x] -1/18(t + 6)(t + 3)(t - 3) dt. Evaluating this integral is a bit complicated. Let's denote F(x) as the antiderivative of f(x): F(x) = ∫[-6,x] -1/18(t + 6)(t + 3)(t - 3) dt. Now, we can find f(x) by differentiating F(x): f(x) = d/dx[F(x)]. To get an explicit equation for f(x), we need to calculate the integral and differentiate the resulting antiderivative. Once you have the equation for f(x), you can plot it on the provided graphing option to verify that it matches the criteria mentioned in the question.
To learn more about derivative, click here: brainly.com/question/2159625
#SPJ11
If we flip a coin eight times, how many possible sequences of eight coin faces (i.e., heads or tails) can we have
Answers
Using the Fundamental Counting Theorem, the number of possible sequences of eight coin faces is of 256.
It is a theorem that states that if there are n things, each with ways to be done, each thing independent of the other, the number of ways they can be done is:
In this problem, there are 8 events, each with 2 possible outcomes, hence:
Hence, the total number of sequences is given by:
Hence, the total number of sequences is given by:
.
Learn more about the Fundamental Counting Theorem at brainly.com/question/24314866
#SPJ4
Find the perimeter of the following figure.

Answers
Answer:
10 meters
Step-by-step explanation:
Perimeter= 3+3+2+2
=10
Have a nice day:)
CAN SOMEONE HELP ME PLEASE!!! I WILL GIVE THE BRAINIEST AND 100 POINTS!!!

Answers
Step-by-step explanation:
the length of hypotenuse =
√(21²+28²) = √(441+784)
= √1225
= 35 yd
the perimeter of triangle =
21+28+35 = 84 yd
the area of triangle =
½×21×28 = 294 yd²
Answer: 35 yd
Step-by-step explanation:
28^2+21^2=1225
√1225
=35
Which equation represents the line that is perpendicular to y=1/5 and passes through (-4,-3)?
10 pts please hurry.
Answers
Answer:
x=-4
Step-by-step explanation:
Just had it on a test and got it write
.Mobile banner ads perform significantly better than desktop banners.
False or true?
Answers
It is false that mobile banner ads perform significantly better than desktop banners.
There is no clear consensus on whether mobile banner ads or desktop banner ads perform better. The effectiveness of banner ads depends on various factors such as the placement of the ad, its design, and the target audience.
However, it is true that mobile usage has been increasing rapidly in recent years, and more people are accessing the internet through their mobile devices than through desktop computers. Therefore, it is important for advertisers to optimize their ads for mobile devices and ensure that they are mobile-responsive.
Nevertheless, it cannot be generalized that mobile banner ads are more effective than desktop banner ads. The effectiveness of an ad should be evaluated on a case-by-case basis, taking into account the specific objectives, target audience, and design of the ad.
Therefore, it is important for advertisers to test their banner ads on both desktop and mobile devices to determine which platform works best for their specific campaign. And the given statement is false.
To learn more about desktop banners here:
brainly.com/question/1171439#
#SPJ11
Is √ 3x² 5y is a polynomial?
Answers
Answer: yes
Step-by-step explanation:
A square mirror has a perimeter of 8 ft how long is each side of the mirror
Answers
Answer:
2 ft
Step-by-step explanation:
Perimeter = 4 * sides
8 ft = 4 * s
side = 2 ft
Answer:
2 ft
Step-by-step explanation:
8/4 = 2
Two angles of a quadrilateral measure 125° and 35°. The other two angles are in a ratio of 3:5. What are the measures of those two angles?
Answers
Answer:
120° and 80°
Step-by-step explanation:
quadrilateral = 360°
125° + 35° = 160°
360° - 160° = 200°
3/5 of 200° = 120°
200° - 120° = 80°
Answer:
Step-by-step explanation:
Finding the missing angles of quadrilateral:
Ratio of other two angles = 3 : 5
Other two angles are 3x , 5x
Sum of all angles of quadrilateral = 360
125 + 35 + 3x + 5x = 360
Combine like terms
160 + 8x = 360
Subtract 160 from both sides
8x = 360 - 160
8x = 200
Divide both sides by 8 to isolate x
x = 200/8
x = 25
5x = 5*25 = 125
3x = 3*25 = 75
The other two angles are 125° , 75°
Please answer the following attached image:

Answers
Answer:
6i
Step-by-step explanation:
\(\sqrt{-36} = \sqrt{36} \sqrt{-1}\)
\(\sqrt{36}\) is 6 and symbol for \(\sqrt{-1}\) is i for imaginary. So your answer will be 6i
Please help asap 7th grade grade maaaaath
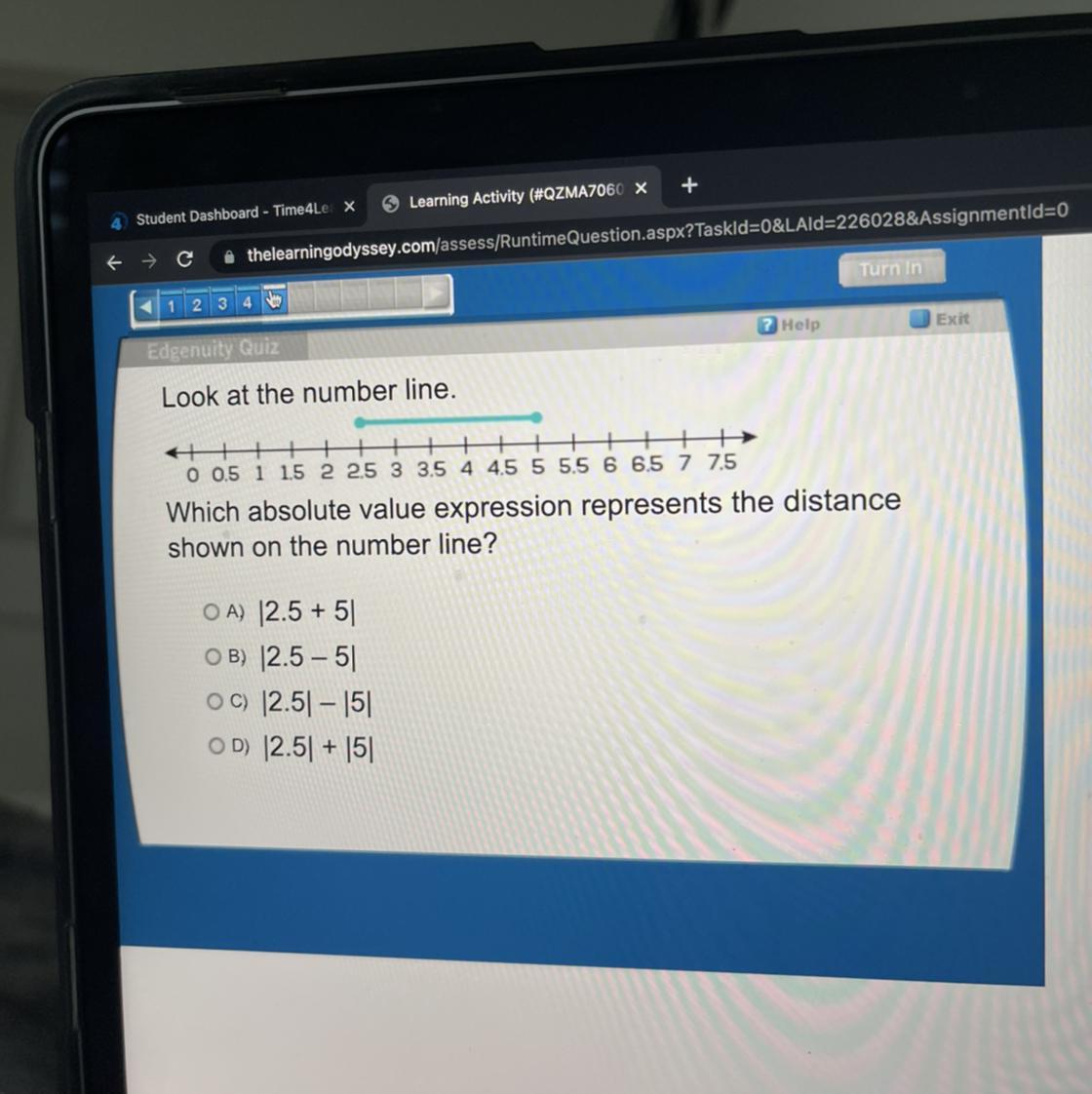
Answers
Answer:
B
Step-by-step explanation:
because (2.5 - 5 = -2.5 )but, since its absolute value the answer is 2.5
Hope this helps! Please let me know if you need more help or think my answer is incorrect. Brainliest would be MUCH appreciated. Have a wonderful day!
Answer:
The answer is B
Step-by-step explanation:
Did this , mark brainliest!:)
Multiplica: (5 ft 6 in) x 4.
Answers
Answer: 22 ft
Step-by-step explanation:
on the trip from detroit to colombus, ohio, mrs smith drove an average speed of 60 mph. returning, her average speed was 55 mph. if it took her 1/3 of an hour longer on the return trip, how far is it from detroit to columbus
Answers
Distance from Detroit to columbus is 220 miles
It is given in the question,
The average speed Mrs. smith drove = 60 mph.
Returning, her average speed was 55 mph.
Time taken = 1/3 of an hour longer on the return trip
We have to Find total distance between Detroit and Columbus
So, Let the distance between Detroit and Columbus be "x" miles
Average speed = 60
So, time taken by her to cover distance of x miles with speed of 60 mph
Time = Distance / speed
=> t = x / 60
She Took x/60 hours to reach Columbus
While returning her speed was 55 mph.
So, time taken by her to cover the same distance but at a speed of 55 mph :
=> t = x / 55
Now we are given that she took 1/3 of hour more while returning .
So, \(\frac{x}{55} - \frac{x}{60} = \frac{1}{3}\)
⇒ x/660 = 1/3
=> x = 660/3
=> x = 220 miles
Hence , Detroit is 220 miles far from Columbus
To know more about distance here
https://brainly.com/question/15172156
#SPJ4
In the diagram below A' B'C'D' is an enlargement of ABCD. AD = 12 cm, |DC| = 8 cm and A'D' = 20 cm Find A' B.

Answers
Scale factor = 5/3, AB = 4√5 cm, and perpendicular distance of scale factor is so A'B' = (20/3)√5 cm.
To find A'B, we want to initially decide the scale element of the growth. We know that Promotion = 12 cm and A'D' = 20 cm, so the scale factor is:
scale factor = A'D'/Promotion = 20 cm/12 cm = 5/3
This implies that each side of A'B'C'D' is 5/3 times the length of the relating side of ABCD.
To find A'B, we can zero in on the level side of the square, which relates to Stomach muscle in ABCD. We know that |DC| = 8 cm, so |BC| = |DC| = 8 cm. Since the scale factor is 5/3, we have:
|A'B'| = (5/3) * |AB|
We can utilize the Pythagorean hypothesis to track down |AB|. Let x be the length of |AB|, then, at that point:
\(x^2 + 8^2 = 12^2\)
Working on this situation, we get:
\(x^2 = 144 - 64 = 80\)
Taking the square base of the two sides, we get:
x = √80 = 4√5
Hence:
|A'B'| = (5/3) * |AB| = (5/3) * 4√5 = (20/3)√5
So the length of A'B' is (20/3)√5 cm.
To learn more about perpendicular distance, refer:
https://brainly.com/question/21406061
#SPJ1
The functiona f(x) and g(x) are shown on the graph.
What is g(x)?
f(x)
10
-5
g(x)
A
-10
A. 9(x) = -x2 - 4
B. g(x) = -x + 4
c. g(x) = (-x)² - 4
D. g(x) = (-x)2 + 4

Answers
Answer:
A. g(x) = -\(x^{2}\) - 4
Step-by-step explanation:
f(x) is flipped, so \(x^{2}\) becomes -\(x^{2}\).
After being flipped, the graph is move down 4 units.
Therefore, g(x) = -\(x^{2}\) - 4
Find the 53rd term of the arithmetic sequence –12, -1, 10, ...
Answers
Answer:
560
Step-by-step explanation:
you listed the first 3, so it's 53 - 3 = 50 and you multiply 50 and 11 (the sequence is +11) to get 550. Add 10 and you get 560!
1. Give an example of a sample space Ω together with a probability rule P and four independent (non-trivial) random variables X, Y, Z and T which are all defined on Ω. (A random variable X : Ω → R is non-trivial if it gets at least two different values with non-zero probability.)
2. With the example in part (1), show that U = XY and V = Z + T are independent. (Show by formulae, not by explanation.)
Answers
1) The example of a sample space Ω together with a probability rule P and four independent (non-trivial) random variables X, Y, Z and T which are all defined on Ω is: Ω = {H, T}, P(H) = P(T) = 1/2
2) U = XY and V = Z + T are independent as:
P(U = XY)P(V = Z + T) = 1/2
P(U = XY, V = Z + T) = P(U = XY)P(V = Z + T)
Here, we have,
from the given information , we get,
Question 1
Ω = {H, T}, P(H) = P(T) = 1/2
X(H) = 0, X(T) = 1
Y(H) = 1, Y(T) = 2
Z(H) = 2, Z(T) = 3
T(H) = 3, T(T) = 4
The example of a sample space Ω together with a probability rule P and four independent (non-trivial) random variables X, Y, Z and T which are all defined on Ω is: Ω = {H, T}, P(H) = P(T) = 1/2
Question 2
P(U = XY) = P(U = 0) + P(U = 2) + P(U = 3) + P(U = 4)
= P(X = 0, Y = 0) + P(X = 0, Y = 2) + P(X = 1, Y = 1) + P(X = 1, Y = 2)
= P(X = 0)P(Y = 0) + P(X = 0)P(Y = 2) + P(X = 1)P(Y = 1) + P(X = 1)
P(Y = 2)
= 1/4 + 1/4 + 1/4 + 1/4
= 1
P(V = Z + T) = P(V = 2) + P(V = 3) + P(V = 4) + P(V = 5)
= P(Z = 2, T = 0) + P(Z = 2, T = 1) + P(Z = 3, T = 0) + P(Z = 3, T = 1)
= P(Z = 2)P(T = 0) + P(Z = 2)P(T = 1) + P(Z = 3)P(T = 0) + P(Z = 3)
P(T =1)
= 1/4 + 1/4 + 1/4 + 1/4
= 1
P(U = XY, V = Z + T) = P(X = 0, Y = 0, Z = 2, T = 0) + P(X = 0, Y = 0, Z = 2, T = 1) + P(X = 0, Y = 2, Z = 2, T = 0) + P(X = 0, Y = 2, Z = 2, T = 1) + P(X = 1, Y = 1, Z = 3, T = 0) + P(X = 1, Y = 1, Z = 3, T = 1) + P(X = 1, Y = 2, Z = 3, T = 0) + P(X = 1, Y = 2, Z = 3, T = 1)
= P(X = 0)P(Y = 0)P(Z = 2)P(T = 0) + P(X = 0)P(Y = 0)P(Z = 2)P(T = 1) + P(X = 0)P(Y = 2)P(Z = 2)P(T = 0) + P(X = 0)P(Y = 2)P(Z = 2)P(T = 1) + P(X = 1)P(Y = 1)P(Z = 3)P(T = 0) + P(X = 1)P(Y = 1)P(Z = 3)P(T = 1) + P(X = 1)P(Y = 2)P(Z = 3)P(T = 0) + P(X = 1)P(Y = 2)P(Z = 3)P(T = 1)
= 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16 + 1/16
= 1/2
U = XY and V = Z + T are independent as:
P(U = XY)P(V = Z + T) = 1/2
P(U = XY, V = Z + T) = P(U = XY)P(V = Z + T)
Learn more about probability here:
brainly.com/question/30034780
#SPJ4