6x^2-19x+3=0
Find both of the x
Answers
Related Questions
which relation is a function
joe's age is 4 years less than twice the age of his brother Tom the sum of their ages 41. how old is Tom
Answers
Answer:
joe age = 2x -4
tom age = x
2x - 4 + x = 41
3x = 45
x = 15
joe = 26 y
tom = 15 y
Tomas estimated that he would need to throw 22.52m in fact he threw 21.36m what is the percentage error
Answers
Answer:
5.15%
Step-by-step explanation:
Difference between estimated throw and actual throw
= estimated - actual
= 22.52 - 21.36
= 1.16 m
As a fraction of estimated throw:
1.16/22.52
As a percentage:
1.16/22.52 x 100 = 5.15%
twenty insurance agents are randomly selected and asked if they own a handgun. fourteen of those surveyed said that they do own a handgun. if an insurance agent is randomly selected, estimate the probability that the agent will own a handgun. round your answer to two decimal places, if necessary.
Answers
The probability is 0.8427.
Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one. Probability has been introduced in Maths to predict how likely events are to happen. The meaning of probability is basically the extent to which something is likely to happen. This is the basic probability theory, which is also used in the probability distribution, where you will learn the possibility of outcomes for a random experiment. To find the probability of a single event to occur, first, we should know the total number of possible outcomes.
Here we are total number of insurance agents = 89
And number of insurance agents do own a handgun = 75
So we asked probability that a insurance agent will own a handgun
Probability = no.of insurance agents/no.of insurance agents who owns a handgun
Probability = 75/89 = 0.8427
The probability that the agent will own a handgun is .84
To learn more about probability visit:brainly.com/question/30034780
#SPJ4
Three times a number plus nine is five
Answers
9. If DF = 61 and EF = 18, find DE.
10. If DE=4x-1, EF = 9, and DF = 9x-22, find
the value of x.
D
11. If DF = 78, DE = 5x-9, and EF = 2x + 10, find EF.
12. If DE= 4x + 10, EF=2x-1, and DF = 9x-15, find DF.

Answers
The obtained answers for the given line segments are as follows:
9. The value of the line segment \(\overline {DE}\) = 43; Where \(\overline { DF}\) = 61 and \(\overline {EF}\)
10. The value of x is 6; Where \(\overline {DE}\) = 4x - 1, \(\overline {EF}\) = 9, and \(\overline { DF}\) = 9x - 22
11. The value of line segment \(\overline {EF}\) = 32; Where \(\overline { DF}\) = 78, \(\overline {DE}\) = 5x - 9, and \(\overline {EF}\) = 2x + 10
12. The value of line segment \(\overline { DF}\) = 57; Where \(\overline {DE}\) = 4x + 10 \(\overline {EF}\) = 2x - 1, and \(\overline { DF}\) = 9x - 15.
What is a line segment?A line segment is a part of a line formed by infinite points with two endpoints at both ends. The line segment is represented by the two endpoints.A line segment has a finite length.Calculation:The calculation for the required values is as follows:
9. Finding \(\overline{DE}\):
It is given that,
\(\overline{DF}\) = 61; \(\overline{EF}\) = 18
From the figure, we can write
\(\overline{DF} = \overline{DE} + \overline{EF}\)
On substituting the given values,
61 = \(\overline{DE}\) + 18
⇒ \(\overline{DE}\) = 61 - 18
∴ \(\overline{DE}\) = 43
10. Finding x:
It is given that,
\(\overline {DE}\) = 4x - 1, \(\overline {EF}\) = 9, and \(\overline { DF}\) = 9x - 22
From the figure we have
\(\overline{DF} = \overline{DE} + \overline{EF}\)
On substituting,
(9x - 22) = (4x - 1) + 9
⇒ 9x - 22 = 4x - 1 + 9
⇒ 9x - 4x = 8 + 22
⇒ 5x = 30
∴ x = 6
11. Finding \(\overline{EF}\):
It is given that,
\(\overline { DF}\) = 78, \(\overline {DE}\) = 5x - 9, and \(\overline {EF}\) = 2x + 10
From the figure we have
\(\overline{DF} = \overline{DE} + \overline{EF}\)
On substituting,
78 = (5x - 9) + (2x + 10)
⇒ 78 = 5x - 9 + 2x + 10
⇒ 7x + 1 = 78
⇒ 7x = 78 - 1
⇒ 7x = 77
∴ x = 11
On substituting x = 11 in \(\overline {EF}\) = 2x + 10; we get
\(\overline {EF}\) = 2(11) + 10
= 22 + 10
= 32
Therefore, the value of the line segment \(\overline {EF}\) is 32.
12. Finding \(\overline {DF}\):
It is given that,
\(\overline {DE}\) = 4x + 10 \(\overline {EF}\) = 2x - 1, and \(\overline { DF}\) = 9x - 15
From the figure we have
\(\overline{DF} = \overline{DE} + \overline{EF}\)
On substituting,
(9x - 15) = (4x + 10) + (2x - 1)
⇒ 9x - 15 = 4x + 10 + 2x - 1
⇒ 9x - 15 = 6x + 9
⇒ 9x - 6x = 9 + 15
⇒ 3x = 24
∴ x = 8
On substituting x = 8 in \(\overline { DF}\) = 9x - 15; we get
\(\overline { DF}\) = 9(8) - 15
= 72 - 15
= 57
Therefore, the value of the line segment \(\overline { DF}\) is 57.
Learn more about line segments here:
https://brainly.com/question/280216
#SPJ9
HELP PLEASE!! ASAP!!

Answers
Answer:
f(x) = -3x+1
Step-by-step explanation:
every straight graph has an equation f(x) = m * x + b
when the graph goes up when you look at it from left to right, m is a positive number. when it goes down, then m is negative.
the value of m you can read when you go 1 to the right and then count how many you need to go up/down to meet the graph. in this picture, you need to go down 3.
So m = -3
b is how many you habe to go up (+) or down (-) from the center point 0
so in this case you see on the picture that the graph is hitting the y line on 1
so your equation is -3x + 1
Elizabeth makes cakes. To make 6 cakes, she uses 7 1/2 cups of sugar. How many cups of sugar are needed to make 1 cake?
Answers
Answer:
1 1/4
Step-by-step explanation:
7 1/2 divided by 6
What is the next value?
2 3 E 4 5 I 6 8
options: O 8 M N
Answers
Answer:
The correct answer is a.
Step-by-step explanation:
The sequence is: 2 3 E 4 5 I 6 8 We can notice that there are numbers and letters alternating in the sequence. The numbers are increasing, and the letters seem to be vowels in alphabetical order. So, the next value should be a letter (vowel) after I, which is O. The correct answer is a.
100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answers
Answer:
x = 42
y = 21
Step-by-step explanation:
Since its a right triangle, we have:
sin x = opposite/hypotenuse
cos x = adjacent/hypotenuse
\(sin (60) = \frac{21\sqrt{3} }{x} \\\\x= \frac{21\sqrt{3} }{sin (60)} \\\\x= \frac{21\sqrt{3} }{\frac{\sqrt{3} }{2} } \\\\x = \frac{21\sqrt{3} *2 }{\sqrt{3} } \\\\x = 21*2\\\\x = 42\)
\(cos (60) = \frac{y}{x}\\\\cos (60) = \frac{y}{42}\\\\y = cos (60)*42 \\\\y = \frac{1}{2} * 42\\\\y = 21\)
A toy train has 8 compartments and an engine that is 8 inches long. Each compartment is 4 inches long. Each compartment is joined by links that are 3 inches long. How long is that train.
Answers
Answer:
64in
Step-by-step explanation:
links=8*3=24
compartments + engine=4*8+8=40
40+24=64
What is the solution to the equation
2x=5
Answers
Answer:
5/2 or 2.5
Step-by-step explanation:
Divide both sides by 2.
A composite figure is shown below.
What is the area of the composite figure?
12 in.
0204 square inches
222 square inches
3 in.
5 in.
228 square inches
4 in. 4 in.
234 square inches
24 in.
8 in.

Answers
Answer:
234 square inches
Step-by-step explanation:
Ok take this shape step by step. First solve the rectangle.
The area of the rectangle would be: 24 * 8 = 192
Rectangle Area: 192
Then, solve the area for the triangle in the middle.
The area of that triangle would be: 8 * 3 divided by 2. You get 8 by the base of the triangle, 4 + 4. 3 is of course, the height. Lastly, you divide this by 2 because that is the formula for the area of a triangle. When you solve, you get 12.
Middle Triangle Area: 12
Then solve for the last triangle.
Doing the same thing, the area for that triangle is 12 * 5 divided by 2. So solve, 12*5 = 60, 60/2 = 30
Last Triangle area: 30
Finnally, add all the areas up,
192 + 12 + 30 = 234
Chase's math teacher finds that there's roughly a linear relationship between theamount of time students spend on their homework and their weekly quiz scores. Thisrelationship can be represented by the equation y = 72 + 64, where y representsthe expected quiz score and a represents hours spent on homework that week. Whatis the meaning of the y-value when 21?

Answers
Given:
\(T=0.31c+36\)where T represents the temperature in degrees Fahrenheit and c represents the number of times the cricket chirps in one minute.
Given that the value of c=148.
The answer is
T is the expected temperature in degrees Fahrenheit if the cricket has chirped 148 times per minute.
What is the conjugate?
a-√a-1

Answers
Answer:
a – bi is a + bi.
Step-by-step explanation:
The complex conjugate of a + bi is a – bi, and similarly the complex conjugate of a a – bi is a + bi.
Mark what answer it is

Answers
2/29
the i is imaginary
An interior designer is redecorating a room that is 26 feet long by 18 feet wide by 9 feet high. At one end of the room is a door that is 6 feet 6 inches high and 4 feet wide. One of the walls contains 2 windows, each of which is 2 feet wide by 2 feet 6 inches high.
A: How much will it cost to carpet the floor if the carpet sells for $18.00 a square yard? $
B: How much will it cost to wallpaper all four walls if wallpaper costs $0.75 per square foot? $
C: How much will it cost to paint the ceiling using paint that sells for $25 per gallon if a quart of paint will cover 88 square feet? $
D: What will be the cost of the entire project? $
Answers
Answer: A: It will cost $936.00 to carpet the floor.
B: It will cost $297.00 to wallpaper all four walls.
C: It will cost $33.25 to paint the ceiling.
D: The cost of the entire project will be $1266.25.
Step-by-step explanation:
To calculate the costs for carpeting, wallpapering, painting, and the overall cost of the project, we need to determine the areas that need to be covered and the corresponding prices for each material.
Given dimensions:
Room length: 26 feet
Room width: 18 feet
Room height: 9 feet
Door dimensions:
Height: 6 feet 6 inches
Width: 4 feet
Window dimensions (each):
Width: 2 feet
Height: 2 feet 6 inches
A: Carpeting the floor:
To find the area of the floor, we multiply the length and width of the room:
Floor area = Length × Width = 26 feet × 18 feet = 468 square feet.
To convert to square yards (since the carpet is sold per square yard), we divide by 9:
Floor area in square yards = 468 square feet / 9 = 52 square yards.
Cost to carpet the floor = Floor area in square yards × Cost per square yard = 52 square yards × $18.00 = $936.00.
B: Wallpapering the walls:
To find the area of the walls, we calculate the perimeter of the room (2 × (Length + Width)) and multiply it by the height of the room:
Wall area = Perimeter × Height = 2 × (26 feet + 18 feet) × 9 feet = 396 square feet.
Cost to wallpaper the walls = Wall area × Cost per square foot = 396 square feet × $0.75 = $297.00.
C: Painting the ceiling:
To find the area of the ceiling, we multiply the length and width of the room:
Ceiling area = Length × Width = 26 feet × 18 feet = 468 square feet.
Since a quart of paint covers 88 square feet, we need to determine the number of quarts required:
Number of quarts = Ceiling area / Coverage per quart = 468 square feet / 88 square feet = 5.32 quarts.
Since a gallon contains 4 quarts, the number of gallons required is 5.32 quarts / 4 quarts = 1.33 gallons.
Cost to paint the ceiling = Number of gallons × Cost per gallon = 1.33 gallons × $25.00 = $33.25.
D: Cost of the entire project:
Total cost = Cost to carpet the floor + Cost to wallpaper the walls + Cost to paint the ceiling
= $936.00 + $297.00 + $33.25 = $1266.25.
Therefore:
A: It will cost $936.00 to carpet the floor.
B: It will cost $297.00 to wallpaper all four walls.
C: It will cost $33.25 to paint the ceiling.
D: The cost of the entire project will be $1266.25.
For more questions on cost
https://brainly.com/question/13574768
#SPJ11
Type the correct answer in each box.
Day Amount
1
$26
2
$23
3
$31
4
$26
5
534
The table shows the amount Bill spent on 5 days last week.
The mean of the amount he spent is $
The mean absolute deviation is $
Reset
Next
Answers
The mean absolute deviation is $106.6.
Given the table shows the amount Bill spent on 5 days last week.
DayAmount12622313126534To find the mean of the amount he spent: The formula for calculating the mean of a given set of values is mean=∑x/n where x represents the values, n represents the number of values, and ∑x represents the sum of the values.
Mean=total sum of values/total number of values Mean=(26+23+31+26+534)/5Mean=640/5Mean=128So,
the mean of the amount he spent is $128.To find the mean absolute deviation: The mean absolute deviation (MAD) is the average distance between each data value and the mean. MAD shows how much the data set deviates from the mean. The formula for calculating the MAD is MAD=∑|xi−m|/n where xi represents the values, m represents the mean, and n represents the number of values. So, the calculation for each day is:
Day Amount Absolute deviation from mean1 26 |128-26|=102 23 |128-23|=105 31 |128-31|=974 26 |128-26|=102 534 |128-534|=406
The sum of all absolute deviations is:
10+10+97+10+406=533The mean absolute deviation (MAD) is: MAD=533/5=106.6So.
For more question deviation
https://brainly.com/question/475676
#SPJ8
For the triangle shown in the picture two angles are given find the third angle without using a protractor.
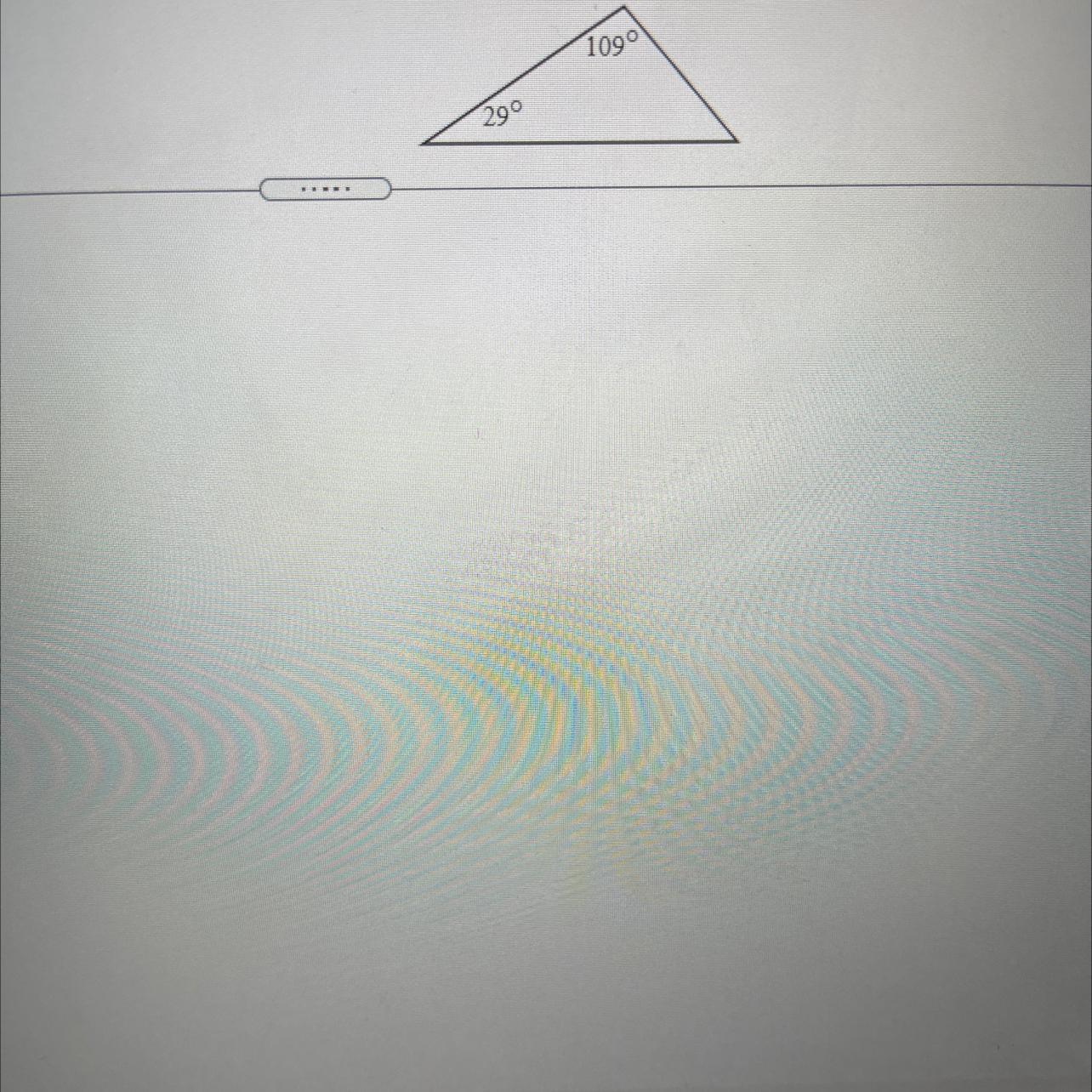
Answers
Let's use x for the missing angle. The sum of the internal angles of a triangle is equal to 180°. Then we have:
\(\begin{gathered} 180^{\circ}=x+29^{\circ}+109^{\circ}=x+138^{\circ} \\ 180^{\circ}=x+138^{\circ} \end{gathered}\)Then if we substract 138° from both sides we get:
\(\begin{gathered} 180^{\circ}-138^{\circ}^{}=x+138^{\circ}-138^{\circ} \\ x=42^{\circ} \end{gathered}\)Then the answer is 42°.
HELPPP!! I'LL MARK U
The area of the figure is ______ square units.

Answers
Answer:
8 units
Step-by-step explanation:
Area of square:
length * width
2 * 3
= 6 units
Area of triangle:
1/2 * base * height
1/2 * 2 * 2
= 2 units
Area of entire shape:
6 + 2
= 8 units
So, the area of the shape is 8 units.
If this answer helped you, please leave a thanks!
Have a GREAT day!!!
7. Hal records the numbers of winners
of a contest in which the player
chooses a marble from a bag.
DA G
Game 1
Game 2
Game 3
Number of Number of
Players
Winners
123
52
155
63
172
65
Based on the data for all three
games, what is the experimental
probability of winning the contest?
Express the answer as a decimal.

Answers
Answer:0.40
Step-by-step explanation:
the experimental probability of winning the contest is 0.4 or 40%.
Define probabilityProbability is a measure of the likelihood or chance of an event occurring. It is a number between 0 and 1, where 0 denotes the impossibility of the occurrence and 1 denotes its certainty. An occurrence is more likely to occur the higher its probability.
Players: 123 + 155 + 172, or 450 total
52 plus 63 plus 65 winners make up the total of 180.
Experimental probability of winning the contest = Total number of winners / Total number of players
Experimental probability of winning the contest = 180 / 450 = 0.4
Hence, the experimental probability of winning the contest is 0.4 or 40%
To know more about occurrence, visit:
https://brainly.com/question/28953812
#SPJ1
Please please help please help me help help me please help me

Answers
Answer:
\(m = \frac{6 - 5}{4 - 1} \\ \color{green} \boxed{m = \frac{1}{3} }\)
which inequality is true p=3.4
Answers
uhhh...p=3.4 is already simplified.
---
hope it helps???
A contractor purchases 3 dozen pairs of padded work gloves for $42.48. He incorrectly calculates the unit price as $14.16 per pair for the expense report. What is the correct unit price? What is the error?
Answers
Answer:
1.18
Step-by-step explanation:
$1.17
Step-by-step explanation:
He divided the total cost by 3 not 3 dozen (36).
(4/5+2/3)×(7/8-2/8) what is it
Answers
(4/5 + 2/3)×(7/8 - 2/8) = 11/12
≅ 0.9166667
-3/10h = 15, what is h?
Answers
-3/10h * 10h = 15 * 10h
-3 = 150h
h = -1/50
Answer:
-50
Step-by-step explanation:
Determine whether the given ordered pair is a solution of the system.
(1, -8)
y = 5x - 13
2x + 4y = - 30
Answers
8.5 x 6.5 i need help with this question
Answers
Answer:
55.25
Step-by-step explanation:
So, all you gotta do is get rid of the decimal, times them both, then add the decimal back into it, and how you do that is you see how many numbers are behind a decimal point in the first place, in this case, it's two (8.5, 6.5) and you got your answer!
Hope this helps! <D
A basket of fruits contains 5 bananas, 8 mangoes, and 7 apples. Two fruits are randomly selected without replacement. Calculate the probability of selecting an apple and a banana.
Answers:
7/80
21/190
3/5
7/76
Answers
The probability of selecting an apple and a banana from the basket is 7/76.
To calculate the probability of selecting an apple and a banana from the basket of fruits, we need to determine the total number of possible outcomes and the number of favorable outcomes.
The total number of fruits in the basket is 5 bananas + 8 mangoes + 7 apples = 20 fruits.
When selecting the first fruit, there are 20 options. Let's say we select an apple. After removing one apple from the basket, there are 19 fruits left.
When selecting the second fruit, there are 19 options. This time, we want to select a banana. Since there are 5 bananas left in the basket, there are 5 favorable outcomes.
To calculate the probability, we divide the number of favorable outcomes by the total number of possible outcomes:
Probability = Number of favorable outcomes / Total number of possible outcomes = (Number of apples) * (Number of bananas) / (Total number of fruits) * (Total number of fruits - 1) = 7/20 * 5/19 = 35/380 = 7/76
For more such questions on probability
https://brainly.com/question/25870256
#SPJ8
A tennis ball can in the shape of a right circular cylinder holds six tennis
balls snugly. If the radius of a tennis ball is 3.2 cm, what percentage of
the can is not occupied by tennis balls?
Answers
Answer: 33 1/3 percent
Step-by-step explanation:
First, we need to find the volume of the tennis ball can, which is a cylinder.
The formula for the volume of a cylinder is pi r^2 h.
The radius of a tennis ball is 3.2 cm, so the radius of the cylinder would be 3.2 cm as well.
The height is equivalent to the height of three tennis balls, which is the diameter of 3 tennis balls. The diameter of one tennis ball is 6.4 cm, and we can multiply this by 6 to get 38.4 as our height.
We can plug in these values to our equation for the volume of the cylinder.
pi * 3.2^2 * 38.4
The volume of the cylinder is 393.216 pi.
Now, we need to find the volume of one tennis ball and multiply that by six.
The volume of a sphere is 4/3 pi r^3
We know our radius, 3.2, so we just have to substitute that into the equation.
4/3 pi 3.2^3 = 4/3 * pi * 32.768 = 43.69 and 2/3 pi for the volume of one tennis ball. If we multiply this by six, we get the volume of all the tennis balls, which is 43.6 and 2/3 *3 = 262.144 pi.
Now we have to find the percentage of the cylinder not occupied, so we can find one percent of the container and divide that by 262.144 pi.
1% of 393.216 = 3.93216
262.144 divided by this = 66 and 2/3, so 33 and 1/3 percent of the can is not occupied. The answer depends on how many places to round to, or whether or not to keep the answer as a fraction.
I need help finding the area

Answers
\( \\ \\ \)
To find:Area of triangle\( \\ \\ \)
We know:-
When base and height of triangle is given we use this formula:
\( \bigstar \boxed{ \rm Area \: of \: triangle = \frac{base \times height}{2} }\)
\( \\ \\ \)
So:-
\( \\ \\ \)
\( \dashrightarrow \sf \: Area \: of \: triangle = \dfrac{base \times height}{2} \\ \)
\( \\ \\ \)
\( \dashrightarrow \sf \: Area \: of \: triangle = \dfrac{7 \times 10}{2} \\ \)
\( \\ \\ \)
\( \dashrightarrow \sf \: Area \: of \: triangle = \dfrac{7 \times 5 \times2 }{2} \\ \)
\( \\ \\ \)
\( \dashrightarrow \sf \: Area \: of \: triangle = \dfrac{7 \times 5 \times\cancel2 }{\cancel2} \\ \)
\( \\ \\ \)
\( \dashrightarrow \sf \: Area \: of \: triangle = \dfrac{7 \times 5 \times1 }{1} \\ \)
\( \\ \\ \)
\( \dashrightarrow \sf \: Area \: of \: triangle =7 \times 5\)
\( \\ \\ \)
\( \dashrightarrow \bf \: Area \: of \: triangle =35 {yd}^{2} \\ \)
\( \\ \\ \)
\( \therefore \underline{\textsf{ \textbf {\: Area \: of \: triangle = \red{35}}} { \red{\bf{yd} }^{ \red2} }}\)
\( \\ \\ \)
know more :-\(\small\begin{gathered}\begin{gathered}\begin{gathered}\boxed{\begin {array}{cc}\\ \dag\quad \Large\underline{\bf \small{Formulas\:of\:Areas:-}}\\ \\ \star\sf Square=(side)^2\\ \\ \star\sf Rectangle=Length\times Breadth \\\\ \star\sf Triangle=\dfrac{1}{2}\times Base\times Height \\\\ \star \sf Scalene\triangle=\sqrt {s (s-a)(s-b)(s-c)}\\ \\ \star \sf Rhombus =\dfrac {1}{2}\times d_1\times d_2 \\\\ \star\sf Rhombus =\:\dfrac {1}{2}d\sqrt {4a^2-d^2}\\ \\ \star\sf Parallelogram =Base\times Height\\\\ \star\sf Trapezium =\dfrac {1}{2}(a+b)\times Height \\ \\ \star\sf Equilateral\:Triangle=\dfrac {\sqrt{3}}{4}(side)^2\end {array}}\end{gathered}\end{gathered}\end{gathered}\)]