5(x-6)+3x=.75(2x-8)
solve.
Answers
Answer:
Step-by-step explanation:
5(x-6)+3x=.75(2x-8)
5x - 30 + 3x = 1.5x - 6
6.5x = 24
x = 3.7
Related Questions
9x2+4y2 = 36
The foci are located at:
O(-V5,0) and (V5, 0)
0 (-V13, 0) and (V13, 0)
0 (0, -V5) and (0, V5)
Answers
Answer:
The foci of the given ellipse = (0 ,-√5 ) and ( 0, √5 )
Step-by-step explanation:
Step(i):-
Given Ellipse 9 x² + 4 y² = 36
\(\frac{9x^{2} }{36} + \frac{4y^{2} }{36} =1\)
⇒ \(\frac{x^{2} }{4} + \frac{y^{2} }{9} = 1\)
Step(ii):-
The Major axis lies on y-axis
Foci of the Formula C² = a² -b² = 9-4 =5
C = √5
The Foci is always lie on the major axis(longest) axis, spaced equally each side of the centre
Given ellipse of the foci is lie on Y- axis
Final answer:-
The foci of the given ellipse = (0 ,-√5 ) and ( 0, √5 )
A tank is full of water. Find the work required to pump the water out of the spout. (Use 9.8 m/s2 for g. Use 1000 kg/m3 as the density of water. Assume r = 6 m and h = 2 m.)
Answers
The work required to pump the water out of the spout is 70.9 * 10⁶ joules which is 71 M Joules approx.
Let the spherical tank be divided into a series of horizontal disks.
Let x be the height of each disk, g = gravity and p = density
Volume of each disk = πr2dx
Where r is the radius of each disk and dx is the thickness
By Pythagoras r² = 6² - x²= 36 -x²
Therefore Volume = π*(36-x²)*dx cubic metres
The distance each disk has to be lifted to escape the top of the spout = 2 + 6-x meters = (8-x)
Work needed to lift each disk to outlet = distance * mass where
mass = volume * density * gravity
= pi(36-x²)*p*g = 9800pi(36-x²)dx
dW = (8-x)* 9800pi(36-x²)dx
Since we have already accounted for the height of the spout, the work required is obtained by integrating the above expression from the bottom of the tank to the top. In other words, - 6 to + 6.
W = ⌠(8-x)*9800pi(36-x2)dx = 9800pi⌠[288 - 36x - 8x² +x³]dx
The odd terms evaluate to zero and we can rewrite the above as 2* I from 0 to 6.
W = 9800pi*2 [288x - 8x³/3] at x = 6 = 1152*19600π Joules = 22579200π joules = 70963200j
Total work required = 70.9 * 10⁶ joules
Visit here to learn more about spherical tank: https://brainly.com/question/11279278
#SPJ4
100 POINTS PLEASE HELP ME ALGEBRA

Answers
The range of the graph of the exponential function is (b) {y | y > 0}
Calculating the range of the graphFrom the question, we have the following parameters that can be used in our computation:
The graph of the exponential function
The rule of an exponential function is that
The domain is the set of all real numbers
This means that the input value can take all real values
However, the range is always greater than the constant term
From the graph, the constant term is 0
So, the range is y > 0
Read more about range at
brainly.com/question/27910766
#SPJ1
What is the equation of a line that is perpendicular to y - 4x+5 and passesthrough the point (8, 3)?

Answers
Equation of line perpendicular to y = 4x+5 passing through point (8,3) is
y = -x/4 + 5
Perpendicular Lines:
A pair of perpendicular lines are straight lines that makes an angle of 90° with one another. Product of slope of perpendicular lines is -1.
that is, m1.m2 = -1
where m1 and m2 are slope of lines
Given equation of line is y = 4x+5 and point (8,3)
we have to find the equation of line perpendicular to y = 4x+5
we know for the line,
y = mx + c
slope = m and c = Intercept on Y axis
so, slope of line y = 4x + 5 is
m = 4
slope of line perpendicular to y = 4x+5 is m1= -1/4
again, we know equation of line passing through (x1,y1),having slope m is
y - y1 = m (x - x1)
thus for slope = -1/4 and point (8,3) equation of line will be
y - 3 = -1/4 (x - 8)
y - 3 = -x/4 + 2
y = -x/4 + 5
Hence, equation of line perpendicular to y = 4x+5 passing through (8,3) is y = -x/4 + 5
option B is correct
To learn more about perpendicular line visit:https://brainly.com/question/18271653
#SPJ9
Measurement of missing angle?

Answers
Answer:
79 degrees
Step-by-step explanation:
180 - 73 - 28 = 79
Because a line is 180 degrees
A triangle LMN with ln = 12 cm,Nm= x cm, Nk = 6cm and Km 8cm
Calculate the value of
(i) x
(ii) o
Answers
The value of x is 9 cm, and angle O is 0 degrees.
To solve the triangle LMN and find the values of x and angle O, we can use the Law of Cosines and the Law of Sines. Let's go step by step:
(i) To find the value of x, we can use the Law of Cosines. According to the Law of Cosines, in a triangle with sides a, b, and c, and angle C opposite to side c, the following equation holds:
c^2 = a^2 + b^2 - 2ab * cos(C)
In our case, we want to find side NM (x), which is opposite to angle N. The given sides and angles are:
LN = 12 cm
NK = 6 cm
KM = 8 cm
Let's denote angle N as angle C, side LN as side a, side NK as side b, and side KM as side c.
Using the Law of Cosines, we can write the equation for side NM (x):
x^2 = 12^2 + 6^2 - 2 * 12 * 6 * cos(N)
We don't know the value of angle N yet, so we need to find it using the Law of Sines.
(ii) To find angle O, we can use the Law of Sines. According to the Law of Sines, in a triangle with sides a, b, and c, and angles A, B, and C, the following equation holds:
sin(A) / a = sin(B) / b = sin(C) / c
In our case, we know angle N and side NK, and we want to find angle O. Let's denote angle O as angle A and side KM as side b.
We can write the equation for angle O:
sin(O) / 8 = sin(N) / 6
Now, let's solve these equations step by step to find the values of x and angle O.
To find angle N, we can use the Law of Sines:
sin(N) / 12 = sin(180 - N - O) / x
Since we know that the angles in a triangle add up to 180 degrees, we can rewrite the equation:
sin(N) / 12 = sin(O) / x
Now, we can substitute the equation for sin(O) from the Law of Sines into the equation for sin(N):
sin(N) / 12 = (6 / 8) * sin(N) / x
Now, we can solve this equation for x:
x = (12 * 6) / 8 = 9 cm
So, the value of x is 9 cm.
To find angle O, we can substitute the value of x into the equation for sin(O) from the Law of Sines:
sin(O) / 8 = sin(N) / 6
sin(O) / 8 = sin(O) / 9
9 * sin(O) = 8 * sin(O)
sin(O) = 0
This implies that angle O is 0 degrees.
Therefore, the value of x is 9 cm, and angle O is 0 degrees.
For more questions on Law of Cosines, click on:
https://brainly.com/question/30766161
#SPJ8
The figure for the given question is provided here :

Gus wrote the following riddle: I am a number between 30 and 60. My ones digit is three less than my tens digit. I am a prime number.
What number does Gus’ riddle describe?
Answers
Answer: 41
Step-by-step explanation:
The woods behind Wendy’s house were 8 miles wide and have an area of 24 mi.² what is the length of the woods 
Answers
Answer:
48 miles
Step-by-step explanation:
i think thats it.
Answer: 4.
Step-by-step explanation: 8+8=16. count how many more until you get to 24, that is 8. Split 8 in half. We get 4.
Hope this helps!
Find the value of x to
the nearest degree.

Answers
Answer:
Step-by-step explanation:
a
PLEASE HELP I WILL MARK YOUR ANSWER AS BRAINLIEST PLEASE BE CORRECT BEFORE ANSWERING
LOOK AT THE BOTTOM
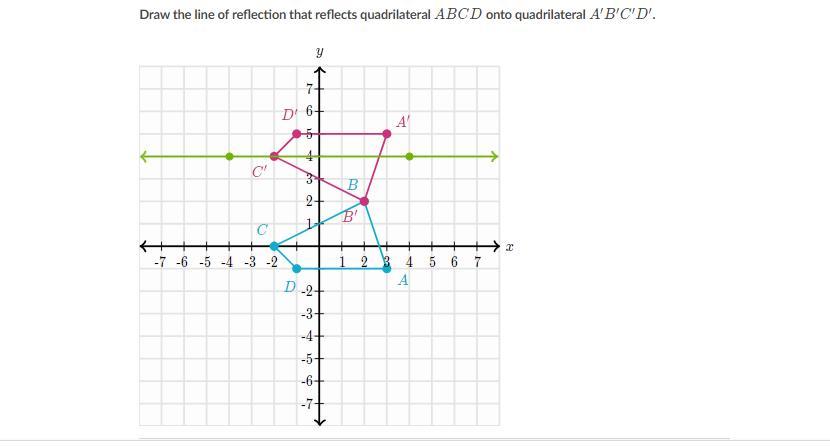
Answers
9514 1404 393
Answer:
y = 2
Step-by-step explanation:
The figure must be flipped top-to-bottom, so the line of reflection must be a horizontal line. Point B must be reflected to itself, so it is on the line of reflection. That means the line of reflection is y = 2.
__
You can draw the line of reflection using any two points that have y-coordinates of 2, for example, (0, 2) and (2, 2).
4. Hockey: How many hockey teams of 6 players can be formed from 14 players without
regard to position played?
Answers
the answer would be 2 but you would have 2 players left over
There will be 3003 hockey teams of 6 players who can be formed from 14 players without regard to the position played.
What are permutation and combination?The variety of possible arrangements of a set is its permutation; order is important in permutations but not in combinations. Combinations are mathematical operations that count the variety of configurations that may be made from a set of objects, where the order of the selection is irrelevant. You can choose any combination of the things in any order. Permutations and combinations are often mistaken.
The number of hockey teams of 6 players can be formed from 14 players without regard to the position played is,
=14C₆
=3003
Thus, there will be 3003 six-player hockey teams that may be assembled from 14 players, regardless of the positions they play.
Learn more about permutation and combination here:
https://brainly.com/question/2295036
#SPJ2
Help me out with 5,6,7 (Geometry)

Answers
Problem 5
A counterexample could be a number like 6. Divide it over 2 and we get 6/2 = 3, which is a whole number. This shows 6 is a multiple of 2. However, 6/4 = 1.5 is not a whole number, so 6 is not divisible by 4. The overall claim is false.
======================================================
Problem 6
Let's say we are subtracting a positive number and a negative number. For instance, let's say we're subtracting 10 and -7
So,
10 minus -7 = 10 - (-7) = 10+7 = 17
When subtracting a negative, the two minus signs cancel to form a plus sign. The result we get is 17, which is larger than the greater number 10. So this is one counterexample that proves the claim to be false.
======================================================
Problem 7
Start with a circle. The circle can be any size. Plot four random points on the circle. The points can be anywhere you want. Let's label those points A,B,C,D. Form quadrilateral ABCD.
Now let's say we pick point A and pull it off the circle and pull it outside the circle. Points B,C and D remain on the circle. This is one example where we cannot draw a circle through this new arrangement of points. The circle goes through B,C, and D just fine; however, it doesn't go through point A. If you try to attempt to get the circle to go through A, then you'll have to pick B,C or D to ignore. In other words, you'll only be able to pick three points that the circle can go through. Therefore, a circle cannot be drawn as described for every quadrilateral.
Note: Any quadrilateral that has all four points on the same circle is known as a cyclic quadrilateral.
Multiply
8.12.30.3
Please help me
Answers
Answer:
8640
Step-by-step explanation:
The domain of this emath equation is

Answers
Answer:
x ≥ 5
Step-by-step explanation:
You want the domain of the equation y = √(x -5) -1.
DomainThe domain of the function is the set of x-values for which it is defined. The square root is not defined for negative values, so the domain is ...
x -5 ≥ 0
x ≥ 5 . . . . . . the domain of this function
__
Additional comment
The range is the set of y-values the function may produce. Here, that set of values is y ≥ -1.
<95141404393>
The students can make 6 tickets from each sheet of paper. How many sheets of paper. How many sheets of paper are needed for 125 tickets?
Answers
Answer:
20.8333333
Step-by-step explanation:
6 x 20.8333333 = 125
Find the coordinates of the center and the measure of the radius for a circle whose equation is x^2+(y-5)^2=9
Answers
Answer:
Coordinates of center: (0, 5)
Radius of circle: 3
log3 (x-4) =2
log(x+3) 8 =1
Answers
Option three log3 + log(x+4) is the equivalent to the logarithm expression log3(x+4).
It is given that logarithm expression is log3(x+4).
It is required to simplify the above equation.
It is another way to represent the power of numbers and we say that 'b' is the logarithm of 'c' with base 'a' if and only if 'a' to the power 'b' equals 'c'.
aᵇ = c
logₐc = b
We have logarithm expression:
log3(x+4)
We know the log property that we can split a logarithm into two logarithms if it contains the product of two numbers ie.
log xy = logx + logy
By using this property we get:
log3(x+4)
= log3 + log(x+4)
Because 3 and (x+4) are two different numbers, not (x+4).
Thus, option three log3 + log(x+4) is the equivalent to the logarithm expression log3(x+4).
Learn more about the Logarithm here:
brainly.com/question/163125
#SPJ1
Solve by addition method
3x+y=8
2x-y=7
Answers
Answer:
(3,-1)
Step-by-step explanation:
So we have the system of equations:
\(3x+y=8\\2x-y=7\)
As directed, add straight down. The y-variable will cancel:
\(5x=15\)
Now, divide both sides by 5. The left cancels:
\(x=3\)
So x is 3.
Now, substitute 3 for x in either of the equations:
\(3x+y=8\)
Substitute 3 for x:
\(3(3)+y=8\)
Multiply:
\(9+y=8\)
Subtract 9 from both sides:
\(y=-1\)
So, our answer is: x=3, y=-1 or (3,-1).
And we are done :)
Simplify the polynomial, then evaluate for x = 2.
x+3x²+2x-3-4x²+6
x² + 3x + 9; 19
x² + 3x + 3; 5
-x² + 3x + 9; 11
O
O
-x² + 3x + 3; 13
Answers
Answer:
x^2 + 3x + 9 = (x + 3)(x + 3)
When x = 2, we have:
(2 + 3) * (2 + 3)
5 * 5
25
The values in the table represent a function.
A 2-column table with 5 rows. The first column is labeled x with entries negative 6, 7, 4, 3, negative 5. The second column is labeled f of x with entries 8, 3, negative 5, negative 2, 12.
Use the drop-down menus to complete the statements.
The ordered pair given in the first row of the table can be written using function notation as
.
f(3) is
.
f(x) = –5 when x is
.
Answers
The correct answers are:
f(-6) = 8f(3) = -2f(x) = -5 when x is 4What is the function?Functions are expressions separated by an equal sign. They have both dependent and independent variables.
How to solve* Lets explain how to solve the problem
- The table of the function has two column
# First column labeled x with entries:
-6 , 7 , 4 , 3 , -5
# Second column labeled f(x) with entries:
8 , 3 , -5 , -2 , 12
∴ The ordered pairs of the function f(x) are:
(-6 , 8) , (7 , 3) , (4 , -5) , (3 , -2) , (-5 , 12)
* Lets complete the missing
∵ The value of x in the first row is -6
∵ The value of f(x) in the first row is 8
∴ The function notation in the 1st row is f(-6) = 8
- The ordered pair given in the first row of the table can be
written using function notation as f(-6) = 8
∵ The ordered pair whose x = 3 is (3 , -2)
∴ The value of f(x) when x = 3 is -2
∴ f(3) = -2
∵ The ordered pair whose f(x) = -5 is (4 , -5)
∴ The value of x when f(x) = -5 is 4
∴ f(x) = -5 when x is 4
To learn more about the function visit, https://brainly.com/question/28278690
how are a common denominator and a common multiple alike and diferent
Answers
Answer:
To find a common denominator of two fractions, you have to find a number that both denominators of the given fractions will divide into. And to find a common multiple, you have to find a number that both given numbers will divide into.
Step-by-step explanation:
Answer:
To find a common denominator of two fractions, you have to find a number that both denominators of the given fractions will divide into. And to find a common multiple, you have to find a number that both given numbers will divide into.
Step-by-step explanation:
In a recipe for pizza sauce, the ratio of cans of tomatoes to teaspoons of oregano is 1:6. How many teaspoons of oregano do you need for eight cans of tomatoes?
Answers
How do you find the scale factor of a dilation without a graph?
Answers
To find the scale factor for a dilation, we find the center point of dilation
A dilation is a transformation that enlarges or reduces a figure in size. This means that the preimage and image are similar and are either reduced or enlarged using a scale factor.
A reduction (think shrinking) is a dilation that creates a smaller image, and an enlargement (think stretch) is a dilation that creates a larger image.
If the scale factor is between 0 and 1 the image is a reduction
If the scale factor is greater than 1, the image is an enlargement
To find the scale factor for a dilation, we find the center point of dilation Measure the distance from this center point to a point on the preimage and also the distance from the center point to a point on the image.
The ratio of these distances gives us the scale factor
Using dilation scale factors, we can shrink or expand a figure to the size we desire, knowing that each angle is congruent, each segment is proportional, the slope of each segment is maintained, and the perimeter of the preimage and image have the same scale factor.
To know more about Scale factor here
https://brainly.com/question/8765466
#SPJ4
An employee started a new job and must enroll in a new family health insurance plan. One of the plans involves prescription drug coverage. The employee estimates that the entire family will fill 10 prescriptions per month, totaling $1,250. The employee has two options to choose from:
Option A: $94 monthly premium; 80% coverage for all prescription costs
Option B: $42 monthly premium; 75% coverage for first $500 in prescription costs, then 85% coverage for all prescription costs over $500
Which option would result in the highest overall cost for the employee, and by how much?
Option A has the highest overall cost by $64.50.
Option B has the highest overall cost by $64.50.
Option A has the highest overall cost by $106.50.
Option B has the highest overall cost by $106.50
Answers
Where the above is given, Option B has the highest overall cost by $685.50.
How is this so ?To find the option would result in the highest overall cost for the employee, we need to calculate the total cost under each option.
Option A
Monthly premium: $94
Prescription coverage: 80%
Total cost under Option A
Monthly premium: $94
Prescription costs covered: 80% of $1,250
= $1,000 (since the employee estimates filling 10 prescriptions totaling $1,250)
Employee's portion of prescription costs: 20% of $1,250 = $250
Overall cost = $94 + $250 = $344
Option B
Monthly premium $42
Prescription coverage 75% for first $500, then 85% for costs over $500
Total cost under Option B
Monthly premium: $42
Prescription costs covered up to $500: 75% of $500 = $375
Prescription costs covered over $500is
85% x ($1,250 - $500)
= 85% of $750
= $637.50
Employee's portion of prescription cost is
($1,250 - $375) + ($750 - $637.50)
= $875 + $112.50
= $987.50
Overall cost: $42 + $987.50 = $1,029.50
Hence Option B has the highest overall cost by $1,029.50 - $344 = $685.50.
Learn more about costs:
https://brainly.com/question/17120857
#SPJ1
suppose c(x) = x^3-10x^2-30x, where x is measured in thousands of units. is there production level that minimizes average cost?
Answers
Answer:
To find out whether there is a production level that minimizes the average cost, we need to find the average cost function first. The average cost (AC) function is given by:
AC(x) = C(x)/x
where C(x) is the cost function and x is the production level.
Substituting the given cost function into the above equation, we get:
AC(x) = (x^3 - 10x^2 - 30x)/x
AC(x) = x^2 - 10x - 30
To find the production level that minimizes the average cost, we need to find the derivative of the average cost function and set it equal to zero:
AC'(x) = 2x - 10
Setting AC'(x) = 0, we get:
2x - 10 = 0
2x = 10
x = 5
Therefore, the critical point of the average cost function is x = 5, which means that there may be a production level that minimizes the average cost. To confirm whether this is a minimum or maximum point, we need to find the second derivative of the average cost function:
AC''(x) = 2
Since AC''(5) = 2 is positive, we can conclude that the critical point x = 5 is a local minimum of the average cost function. Therefore, there is a production level of 5,000 units that minimizes the average cost
Movies at the rental store are $3.75 each. Snacks and drinks are $1.89 each. Round each amount to the nearest dollar to estimate the cost to rent 3 movies and buy popcorn, a soda, and a candy bar.
Answers
Answer:
$14.00
Step-by-step explanation:
First you round 3.75 to 4.00 because 7 is greater than 5 so it would turn the 3 to 4 than add the zeros it's 4.00. Second You multiply by three so 4.00 × 3 you will get 12.00. Than you round 1.89 to 2.00 because 8 is greater than 5 so it would turn to the 1 to the 2 than add the zeros it's 2.00. Finally you add them together and get $14.00
7x-5=30
I need this explained for me please
Answers
Step-by-step explanation:
7x-5=30
Firstly -5 will cross the equality sign and become +5. so we'll have
7x=30+5=35
7x=35 we'll divide both sides by 7
giving u
7x/7=35/7
=x=5
therefore x=5.
CONFIRMATION
7*5-5=30
PLS MARK ME AS BRAINLIEST
Answer:
x = 5.Step-by-step explanation:
Solve for X:
7x - 5 = 30= 7 * x= 7(5)= 35 - 5= 30x = 5.Hence, answer is x = 5.Look at the tape diagram below for the number of boys and the number of girls in a school. Find total number of students in the school.

Answers
a. 8
b. 9
c. 7
d. 6

Answers
Answer:
a. 8
Step-by-step explanation:
1+1 = 2
1+2 = 3
2+3 = 5
3+5 = 8
***Need answer and help to understand

Answers
Answer:
a. given ∠1≅∠2, the converse of the corresponding angles theorem shows l║m.
Step-by-step explanation:
There are several things you need to know to be able to answer this question.
corresponding angles where a transversal crosses (parallel) lines are angles that are in the same direction from the points of intersection. Here angles 1 and 2 are both "northwest" of the points of intersection, so are corresponding angles.the "corresponding angles theorem" tells you "if the lines are parallel, then corresponding angles at a transversal are congruent."the converse of a theorem "if A, then B" is "if B, then A". Here, the converse of the "corresponding angles theorem" is "if the corresponding angles at a transversal are congruent, then the lines are parallel."__
You are given ∠1 ≅ ∠2, so the hypothesis of the converse of the corresponding angles theorem is already true. The conclusion that the lines are parallel is what you are asked to prove. To prove that, you only need to identify the angles as being corresponding, and invoke the theorem. The logic matches answer choice A.
∠1≅∠2 is given. The diagram shows ∠1 and ∠2 are corresponding angles, so by the converse of the Corresponding Angles Theorem, l║m.